Сравнительный анализ применения моделей Лихтенеккера и Лихтенеккера – Асаада для теоретической оценки эффективной теплопроводности горных пород

Гусак С. А. Сравнительный анализ применения моделей Лихтенеккера и Лихтенеккера – Асаада для теоретической оценки эффективной теплопроводности горных пород. Вестник МГТУ. 2024. Т. 27, № 1. С. 103–112. DOI:

e-mail: , ORCID:

Gusak, S. A. 2024. Comparative analysis of the application of the Lichtenecker and Lichtenecker – Asaad models for the theoretical assessment of the rocks effective thermal conductivity. Vestnik of MSTU, 27(1), pp. 103–112. (In Russ.) DOI:

При строительстве и эксплуатации подземных комплексов различного назначения, особенно при их размещении в условиях криолитозоны, неизбежно возникают процессы теплового взаимодействия подземных сооружений с породным массивом. Значение этого фактора подтверждается, в частности, опытом эксплуатации единственной в нашей стране подземной атомной станции на Красноярском горнохимическом комбинате, который показал, что неучет теплового фактора даже при нормальной эксплуатации может приводить к ошибкам в прогнозировании напряженно-деформированного состояния породного массива и условий работы ограждающих конструкций ( Зверев, 1995 ).

При всем разнообразии научно-технических задач, связанных с прогнозной оценкой температурного поля породного массива, необходимым условием для количественного определения изменений температуры во времени является знание, в частности, коэффициента теплопроводности (далее – теплопроводность) горных пород. Зачастую в условиях отсутствия измерений теплопроводности при создании теплофизических моделей используются литературные данные по сходным литолого-фациальным комплексам. Как отмечается в работе ( Дучков и др., 2014 ), интенсивное изучение теплопроводности горных пород началось в середине прошлого столетия в связи с развитием геотермических исследований, ориентированных в основном на оценку плотности теплового потока, который рассчитывается по измерениям геотермического градиента в скважинах и теплопроводности горных пород, вскрытых этими скважинами. Накапливавшиеся со временем результаты измерений в разных лабораториях периодически обобщались, что позволяло при отсутствии необходимой экспериментальной информации пользоваться этими справочными данными для оценки величины теплового потока.

Другой метод определения теплопроводности горных пород базируется на теоретической оценке эффективной теплопроводности пород с использованием различных моделей, связанных с определением теплопроводности на основе данных о содержании и составе породообразующих минералов и пористости, характеризующих многокомпонентную систему. Наиболее широкое применение получила модель среднего геометрического, которая часто называется моделью Лихтенеккера (Lichtenecker К.). В этой модели зависимость эффективной теплопроводности горной породы λ от теплопроводности матрицы (минерального скелета) λ m , теплопроводности флюида в поровом пространстве λ f и пористости породы φ (отн. ед.) представлена в виде простого математического выражения

λ = λ ¹ m ^{- φ} ⋅ λ ^φ f . (1)

Формула (1), которая применялась к широкому спектру смесей, включая биологические материалы, горные породы и минералы, а также композиционные материалы на основе пластмасс ( Guo et al., 2017; Fuchs et al., 2015; Fuchs et al., 2013; Pechnig et al., 2007; Popov et al., 2003; Zhanga et al., 2018 ), долгое время считалась полуэмпирической по природе, поскольку, по мнению критиков, не имела какого-либо теоретического обоснования. В дальнейшем был выполнен ряд исследований, направленных на оценку и обоснование более прочной теоретической основы формулы Лихтенеккера ( Goncharenko et al., 2000; Leão et al., 2015; Simpkin, 2010; Zakri et al., 1998 ).

Однако, по мнению ряда российских и зарубежных специалистов, модель Лихтенеккера не может быть использована для достаточно корректной оценки теплопроводности горных пород, поскольку эта модель не учитывает текстурно-структурных особенностей неоднородных сред. Для учета этих особенностей была создана модифицированная теоретическая модель Лихтенеккера – Асаада, которая, по мнению различных специалистов, обеспечивает существенно более точные оценки и отличается от модели Лихтенеккера включением структурного фактора f следующим образом:

_{λ = λ} 1 _m - f φ _{⋅ λ} f_f φ _{. (2)}

В настоящей работе выполнена расчетно-аналитическая оценка, целью которой является анализ условий и ограничений применения моделей Лихтенеккера и Лихтенеккера – Асаада для прогноза теплопроводности горных пород. Для сравнительной оценки рассмотрены результаты экспериментальных исследований теплопроводности водонасыщенных карбонатных пород (известняк, доломит) из бассейна Molasse на юго-западе Германии, импактной структуры Чиксулуб (полуостров Юкатан, Мексика) и баженовской свиты (Западная Сибирь, Россия).

Экспериментальные исследования теплопроводности карбонатных пород

В работе немецких специалистов (Pechnig et al., 2007), посвященной оценке применимости теоретических моделей, было исследовано около 280 образцов горных пород из бассейна Molasse на юго-западе Германии. Керновые образцы изучались с помощью теплового и петрофизического сканирования с высоким разрешением по теплопроводности, плотности, пористости и скорости звука в породах в сухом и водонасыщенном состоянии. Результаты анализа минералогического состава пород позволили сравнить измеренную теплопроводность с вычисленными значениями теплопроводности на основе различных моделей смешения: среднее арифметическое, среднее геометрическое и среднее гармоническое. При этом было установлено, что для известняков и доломитов модель Лихтенеккера показывает наилучшее согласие с экспериментом независимо от их стратиграфического возраста и генетического происхождения горной породы.

Для учета эффектов геометрии пор и литификации осадочных пород (процесс превращения рыхлых осадков в твердые горные породы) в работе ( Pechnig et al., 2007 ) использована модель

Лихтенеккера – Асаада (формула (2)), на основе которой авторы выполнили численное моделирование для извлечения λ _m и f из лабораторных данных. Результаты моделирования для теплопроводности матрицы и f -фактора приведены в таблице.

Таблица. Результаты моделирования методом Монте-Карло, определяющие параметры модели Лихтенеккера – Асаада ( f -фактор (среднее ± стандартное отклонение) и теплопроводность матрицы породы) ( Pechnig et al., 2007 )

Table. Results of the Monte-Carlo simulations of matrix thermal conductivity and f -factor (mean and standard deviation) according to Lichtenecker – Asaad model ( Pechnig et al., 2007 )

Тип породы	Теплопроводность матрицы, Вт/(м·К)	f -фактор
Известняк	2,63 ± 0,13	0,77 ± 0,26
Доломит	3,71 ± 0,25	0,95 ± 0,13

В работе (Popov et al., 2011) приведены экспериментальные данные по теплопроводности доломитов и известняков импактной структуры Чиксулуб (полуостров Юкатан, Мексика). В этой работе описаны результаты измерений тепловых свойств кернов исследовательской скважины Yaxcopoil-1 (глубина 1 511 м), пробуренной в структуре Чиксулуб. На 451 сухом и водонасыщенном керне из интервала глубин 404–1 511 м были измерены теплопроводность, температуропроводность, объемная теплоемкость, коэффициент термической анизотропии, коэффициент термической неоднородности и, кроме того, пористость и плотность. Выполненные исследования показали, что осадочные породы, пересеченные скважиной Yaxcopoil-1, характеризуются значительными вариациями тепловых свойств, которые обусловлены изменчивостью пористости и литологии пород и демонстрируют разделение пласта на предударные и постударные участки по своим тепловым свойствам и пористости.

На основе корреляции между теплопроводностью и пористостью водонасыщенных пород авторами работы ( Popov et al., 2011 ) получены следующие уравнения регрессии:

– для доломита:

λ(ϕ) = 4,87е–0,018ϕ;                                                (3)

– для известняка:

λ(ϕ) = –0,028ϕ + 2,65.                                      (4)

На основе полученных уравнений регрессии авторами работы была оценена теплопроводность матрицы пород: 4,7 Вт/(м·К) для доломитов и 2,61 Вт/(м·К) для известняков.

В работе ( Попов и др., 2017 ) приведены результаты теплофизических исследований образцов стандартного керна, целью которых, в частности, являлась оценка адекватности теоретических моделей теплопроводности реальным свойствам пород. На основе результатов изучения коллекции из 73 образцов карбонатных пород баженовской свиты (Западная Сибирь, Россия) получены уравнения регрессии, устанавливающие зависимость между теплопроводностью и пористостью для сухих, нефте-и водонасыщенных пород. При помощи этих уравнений выполнена оценка теплопроводности матрицы пород и подобраны значения структурного фактора f . В частности, для водонасыщенных карбонатных пород баженовской свиты оцененное значение матрицы пород составило 3,1 Вт/(м ⋅ К), а подобранная величина фактора f – 0,51.

Как отмечалось ранее, привлекательная простота и возможность применения модели Лихтенеккера для экспрессных инженерных оценок обусловливают ее широкое применение, включая геофизические приложения для горных пород и минералов. Ее использование для теоретической оценки эффективной теплопроводности горных пород различного типа было рекомендовано многими исследователями. Вместе с тем, по мнению ряда специалистов, эта модель не может быть использована для достаточно корректной оценки теплопроводности горных пород. Так, в работе ( Попов и др., 2017 ) отмечается, что причина ограниченности модели Лихтенеккера состоит, в частности, в том, что теплопроводность минеральной матрицы породы зависит не только от ее минерального состава, но и от формы минеральных зерен, межзернового контактного теплового сопротивления, степени тепловой анизотропии пород.

С целью оценки условий и ограничений применения модели Лихтенеккера (формула (1)) для прогнозных расчетов теплопроводности карбонатных пород в настоящей работе использованы результаты рассмотренных ранее экспериментальных исследований, по которым имелась достаточная информация для сравнительного анализа. Сопоставительные оценки выполнялись на основе корреляционных соотношений (в дальнейшем – экспериментальные данные), полученных авторами экспериментальных исследований в результате анализа петрофизических свойств карбонатных пород. При этом рассматривались водонасыщенные породы с теплопроводностью воды в поровом пространстве λ f = 0,6 Вт/(м·К).

Так, с учетом данных таблицы, полученных авторами работы ( Pechnig et al., 2007 ), формула Лихтенеккера – Асаада (2) для оценки зависимости теплопроводности пород λ из бассейна Molasse от пористости φ и структурного фактора f может быть записана в следующем виде:

– для доломита:

λ( φ ) = 3,71 ^{(1–0,95 φ )} · 0,6 ^{0,95 φ} ;                                             (5)

– для известняка:

λ( φ ) = 2,63 ^{(1-0,77 φ )} · 0,6^{0,77 φ} .                                              (6)

Результаты оценки теплопроводности пород по формулам (1), (5) и (6) приведены на рис. 1.

Теплопроводность, Вт/(м ⋅ К)

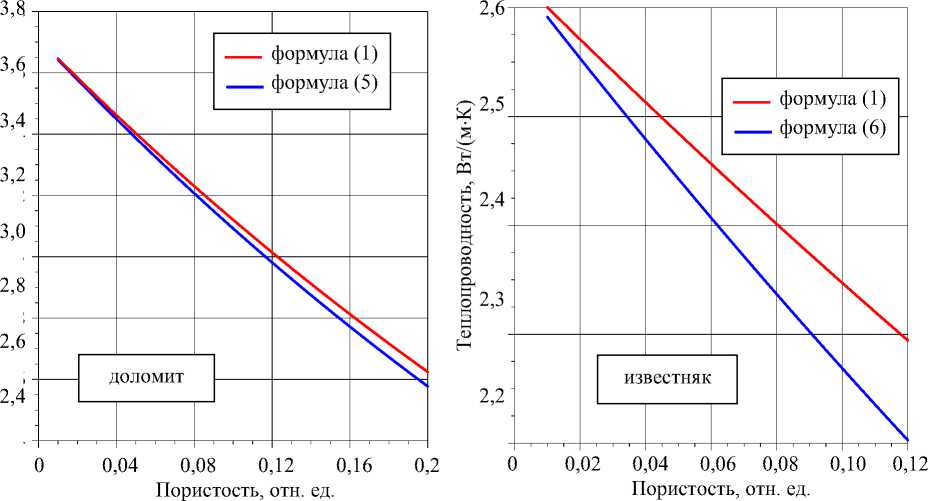
Рис. 1. Зависимость теплопроводности карбонатных пород бассейна Molasse от пористости, вычисленной по модели Лихтенеккера (формула (1)) и по экспериментальным данным (формулы (5) и (6))

Fig. 1. Dependence of thermal conductivity of carbonate rocks of the Molasse basin on porosity calculated using the Lichtenecker model (formula (1)) and experimental data (formulas (5) and (6))

Аналогичные сравнительные оценки были выполнены на примере экспериментальных данных по теплопроводности доломитов и известняков импактной структуры Чиксулуб. Результаты сопоставительных расчетов по уравнениям регрессии (3 и 4) и с помощью модели Лихтенеккера при оцененной авторами работы ( Popov et al., 2011 ) теплопроводности карбонатных пород приведены на рис. 2.

C учетом приведенных ранее значений теплопроводности матрицы пород и структурного фактора f , полученных авторами работы ( Попов и др., 2017 ) на основе регрессионного анализа образцов карбонатных пород баженовской свиты (Западная Сибирь, Россия), формула Лихтенеккера – Асаада для теоретической оценки теплопроводности таких пород в водонасыщенном состоянии может быть записана в следующем виде:

λ( φ ) = 3,1^{(1–0,51 φ )} · 0,6 ^{0,51 φ} .                                              (7)

Результаты расчетов теплопроводности карбонатных пород баженовской свиты по формулам (1) и (7) приведены на рис. 3.

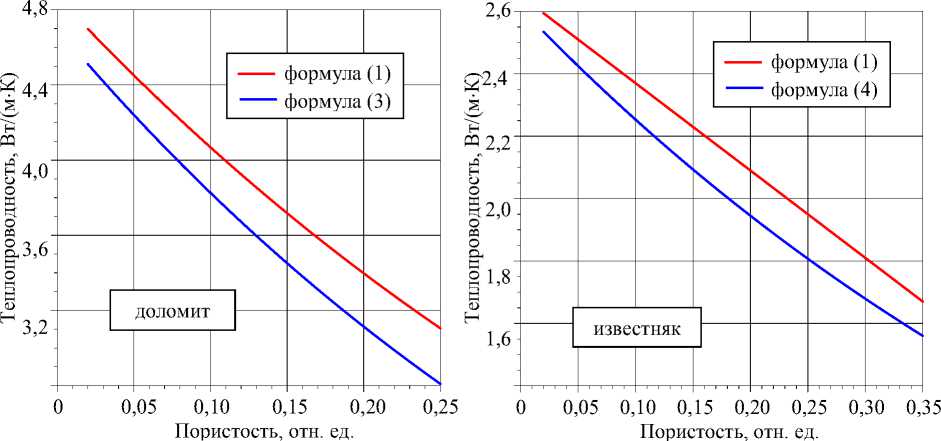
Рис. 2. Зависимость теплопроводности карбонатных пород импактной структуры Чиксулуб от пористости, вычисленной по модели Лихтенеккера (формула (1)) и по экспериментальным данным (формулы (3) и (4))

Fig. 2. Dependence of thermal conductivity of carbonate rocks of the Chicxulub impact structure on porosity calculated using the Lichtenecker model (formula (1)) and experimental data (formulas (3) and (4))

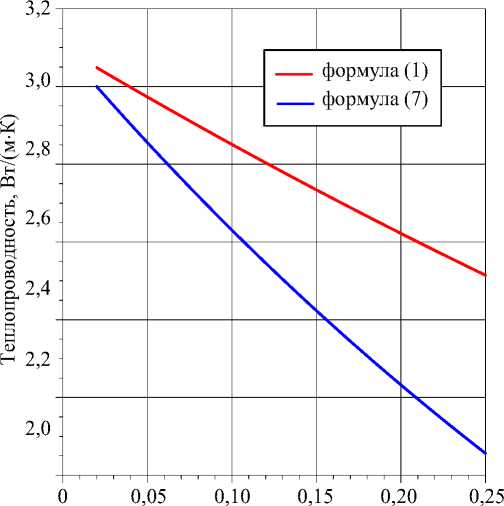
Пористость, отн. ед.

Рис. 3. Зависимость теплопроводности карбонатных пород баженовской свиты от пористости, вычисленной по модели Лихтенеккера (формула (1)) и по экспериментальным данным (формула (7)) Fig. 3. Dependence of thermal conductivity of carbonate rocks of the Bazhenov formation on porosity calculated using the Lichtenecker model (formula (1)) and experimental data (formula (7))

Как видно из рис. 1–3, по мере увеличения пористости возрастают различия в теплопроводности пород, вычисленных по модели Лихтенеккера и экспериментальным данным. Применение формулы Лихтенеккера для сильнопористых пород может приводить к расхождению в расчетных и экспериментальных данных по теплопроводности пород более 14 %. При пористости менее 10 % это расхождение не превышает 8 %. При этом, как и в большинстве других исследований, модель Лихтенеккера прогнозирует более низкие значения эффективной теплопроводности горных пород. По результатам исследований, выполненных на примере карбонатных пород баженовской свиты, в работе (Попов и др., 2017) делается вывод, что модель Лихтенеккера - Асаада дает существенно более точные оценки по сравнению с моделью Лихтенеккера.

В настоящей работе рассмотрено влияние различных параметров модели Лихтенеккера - Асаада на погрешность теоретической оценки эффективной теплопроводности породы.

Методика оценки

В работе ( Попов и др., 2017) отмечается, что для успешного применения модели Лихтенеккера -Асаада необходимы предварительные экспериментальные исследования теплопроводности на представительной выборке изучаемого типа пород с применением прецизионного измерительного оборудования для определения фактора f , соответствующего данному типу пород и конкретному поровому флюиду.

Последнее замечание имеет принципиальное значение для оценки условий и ограничений в применении модели Лихтенеккера. Из формул (1) и (2) со всей очевидностью следует, что различия в прогнозной оценке эффективной теплопроводности пород с помощью моделей Лихтенеккера и Лихтенеккера - Асаада определяются надежностью и точностью определения фактора f

Для анализа влияния различных параметров на погрешность определения фактора f в настоящей работе использован методический подход, предложенный в работах ( Новиков, 2009; Столяров и др., 2007 . Так, для оценки неопределенности 5 f в результатах определения фактора f в зависимости от относительной погрешности оценки теплопроводности минерального скелета (матрицы) породы 5Л m предложена следующая формула:

5 f = К 1 • 5Л m ,

где

K

λ

1n— ^x f

1n(^) . 1n(W л ^        л

Л - эффективная теплопроводность породы; Л m - теплопроводность матрицы породы; Л f - теплопроводность порового флюида.

Согласно выражению (2), которое формализует модель Лихтенеккера - Асаада, неопределенность в оценке фактора f должна оказывать влияние на погрешность оценки эффективной теплопроводности породы δλ . Для оценки взаимосвязи этих параметров использована зависимость, предложенная в работах ( Новиков, 2009; Столяров и др., 2007 ):

5Л = К у • 5 f,                                              (10)

где к/=фМ^У                      <п>

Результаты оценки и обсуждение

Из выражений (8) и (9) следует, что при заданной теплопроводности порового флюида (в частности, воды - для водонасыщенных пород), которая в несколько раз меньше теплопроводности матрицы и эффективной теплопроводности карбонатных пород, основным фактором, определяющим зависимость погрешности оценки фактора f от неопределенности в оценке 2 m , является соотношение Л / Л m .

На основе экспериментальных данных по эффективной теплопроводности рассматриваемых карбонатных пород, для которых были оценены теплопроводности матрицы пород ( Попов и др., 2017; Pechnig et al., 2007; Popov et al., 2011 ), в настоящей работе с помощью формулы (9) выполнена оценка зависимости коэффициента К 1 от соотношения Л/Л_m . Общий характер такой зависимости иллюстрируют данные, приведенные на рис. 4, которые показывают резкое повышение погрешности в оценке фактора f с увеличением отношения Л/Л_m , что для водонасыщенных горных пород является отражением обратной зависимости коэффициента К 1 от пористости геоматериала. Так, например, при отношении Л/Л_m для карбонатных пород баженовской свиты в диапазоне от 0,92 до 0,96 (уменьшение пористости от 10 до 5 %) значение коэффициента К 1 увеличивается с 11,3 до 23,3. Это значит, что неопределенность в оценке теплопроводности матрицы на уровне 15-25 %, которая в большинстве реальных случаев является вполне удовлетворительным результатом ( Столяров и др., 2007) , может приводить к погрешности 170-280 % в оценке фактора f при пористости породы 10 % и 350-580 % при пористости 5 %.

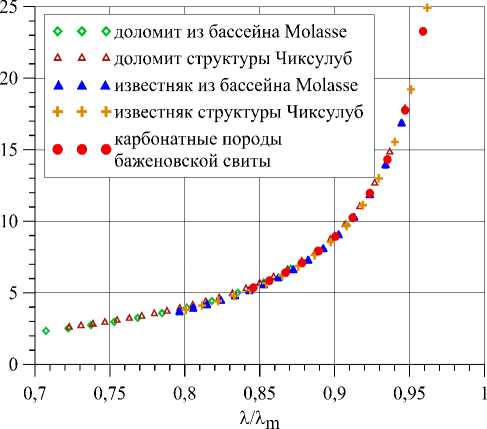
Рис. 4. Зависимость коэффициента К ₁ от отношения эффективной теплопроводности водонасыщенной породы к теплопроводности ее матрицы

Fig. 4. Dependence of coefficient K ₁ on the ratio of the effective thermal conductivity of a water-saturated rock to the thermal conductivity of its matrix

Результаты расчетов коэффициента К f в зависимости от соотношения λ / λ _m для карбонатных пород баженовской свиты и бассейна Molasse при оцененных значениях фактора f , которые использованы в формулах (5–7), приведены на рис. 5.

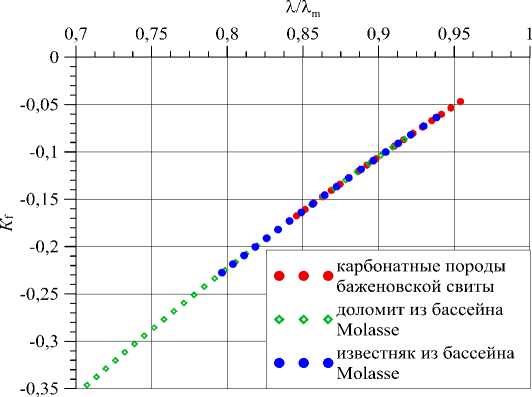
Рис. 5. Зависимость коэффициента К f от отношения эффективной теплопроводности водонасыщенной породы к теплопроводности ее матрицы

Fig. 5. Dependence of the K f coefficient on the ratio of the effective thermal conductivity of water-saturated rock to the thermal conductivity of its matrix

На рис. 5 видно, что в отличие от влияния неопределенности в оценке теплопроводности матрицы породы на погрешность оценки фактора f , влияние структурного фактора f на неопределенность в оценке эффективной теплопроводности породы уменьшается при повышении соотношения λ / λ m .

В дополнение к расчетным данным представляет интерес рассмотрение результатов теоретического анализа различных параметров модели Лихтенеккера – Асаада и, в частности, связи структурного фактора f с геометрическими характеристиками порового пространства ( Новиков, 2009 ). В своем анализе автор этой работы базировался на теоретической модели эффективной теплопроводности многокомпонентной среды, основанной на теории эффективных сред, которая позволяет рассчитывать эффективное значение теплопроводности, исходя из данных о минеральном составе, пористости и геометрических характеристиках порового пространства (аспектное отношение и функция его распределения).

При построении модели предполагалось, что минеральные зерна, поры и трещины имеют форму эллипсоидов вращения, которая описывается аспектным отношением, представляющим собой отношение полуоси, нормально ориентированной к плоскости симметрии эллипсоида, и полуоси, лежащей в плоскости симметрии. Поскольку при анализе рассматривались изотропные образцы горных пород, для ориентации эллипсоидов использовалась случайная функция распределения.

На основе использованной теоретической модели проведены расчеты эффективной теплопроводности пород с разным аспектным отношением пор/трещин, диапазон которого варьировался от 0,001 до 1 при вариации значений теплопроводности минерального скелета от 3 до 7 Вт/(м·К). Результаты расчетов показали, что влияние аспектного отношения пор/трещин на эффективную теплопроводность породы зависит от отношения теплопроводностей минерального скелета и флюида в поровом пространстве. При этом для водонасыщенных пород наблюдается минимальное влияние аспектного отношения пор/трещин. Для таких пород наибольшее влияние геометрических характеристик порового пространства на эффективную теплопроводность породы наблюдается при пористости от 10 до 40 %. При пористости менее 10 % расхождение в величине эффективной теплопроводности породы во всем диапазоне аспектного отношения пор/трещин не превышает 4 %. В этом случае теплопроводность матрицы выступает в качестве доминирующего фактора.

Заключение

Выполнена расчетно-аналитическая оценка применения моделей Лихтенеккера и Лихтенеккера – Асаада для прогноза эффективной теплопроводности водонасыщенных горных пород. Обобщение результатов оценки позволяет сделать вывод, что использование модели Лихтенеккера – Асаада может приводить к погрешности оценки эффективной теплопроводности водонасыщенных непористых и слабопористых горных пород (φ ≤ 0,1), которая сопоставима или превышает относительное расхождение в теоретической оценке теплопроводности различных горных пород по экспериментальным данным и по модели Лихтенеккера. Модель Лихтенеккера – Асаада позволяет обеспечить высокое качество теоретической оценки теплопроводности горных пород при наличии экспериментальных данных, полученных на основе использования измерительного оборудования, обеспечивающего высокоточное определение структурного фактора. При отсутствии соответствующих экспериментальных данных на стадии предпроектных исследований для достаточно корректных инженерных оценок теплопроводности водонасыщенных слабопористых горных пород, которые представляют наибольший практический интерес для подземного размещения особо ответственных объектов, может быть применена модель Лихтенеккера.

Работа выполнена в рамках темы НИР № 0226-2019-0026 "Развитие методологии создания подземных комплексов для атомных станций малой мощности в Арктике ".