Сравнительный анализ точности наблюдений земли многоспутниковыми системами на высокоэллиптических орбитах

Данная статья является дальнейшим развитием работы [1]. Результаты, приведённые в статье, основаны на представленном там критерии оценки точности наблюдений, который не связан с особенностями бортовой аппаратуры наблюдения. Данный критерий позволяет получить сравнительные оценки точности для различных типов спутниковых систем наблюдения (ССН) на основе расчёта точности определения географических координат объектов и моделирования сравнительных точностных характеристик реализуемых ССН. В статье представлены результаты проектно-баллистического анализа по выбору возможных структур прикладных ССН на эллиптических орбитах типа «Молния» для наблюдения неподвижных объектов с определением их координат на Земле и/или в приземном слое. Приведённые результаты могут использоваться для начального выбора структур оптимальных ССН на высокоэллиптических орбитах (ВЭО).

Критерий точности наблюдения спутниковых систем наблюдения

Геометрия обзора показана на рис. 1.

Сигналы, снимаемые с целевой аппаратуры, являются прямоугольными координатами Р _n и P _b .

Для одиночного наблюдения объекта с одного КА имеем:

где

h = P ϕγ P ρ T,

P ϕγ

sin ϕ cos γ sin ϕ sin γ

– cos ϕ sin γ cos ϕ cos γ

1 cosϕ –sinϕcosγ –sinϕsinγ P = ρρ 0 sinγ cosϕ cosγ cosϕ ; (2) rT    rT uxrT   OXrT

I ^r T |       ^{| г}т1 ^{|ux r} T | ^{|ux r} T |

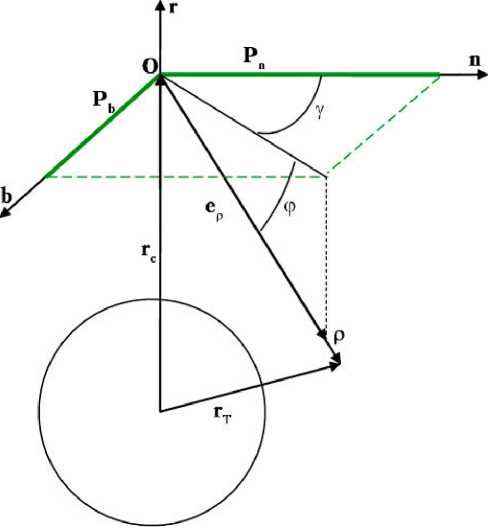
Рис. 1. Геометрия обзора: r_c — геоцентрический радиус-вектор космического аппарата (КА); r_T — геоцентрический радиус-вектор объекта наблюдения; n , r , b — орты орбитальной системы координат КА; ρ — вектор линии визирования на объект; e _ρ — единичный вектор направления линии визирования; ϕ , γ — углы, определяющие положение линии визирования относительно орбитальной системы координат КА

При наличии одновременных измерений с двух и более КА линейное уравнение для ошибок измерений

ΔP = HΔrT, где Н — матрица следующего вида:

H = [h1 h2 … hk], здесь hi — матрица вида (1) и k — количество одновременных измерений. Матрица Н имеет размерность 2×3k.

Квадрат ошибок измерений

Δr _T² = Δr _T ^T ⋅ Δr _T = Δp ^T ( H ^T H )^–1 Δp = Δp ^T M ^–1 Δp .

Для среднеквадратических отклонений ошибок измерений и ошибок определения координат объекта наблюдения имеется соотношение:

о _т<  ^ trace[( M ) * ] о p = D о p .

Используемый критерий оценки точности наблюдений более подробно описан в статье [1].

Аналогично ССН на круговых орбитах при моделировании ССН на ВЭО рассматривались горизонтальные составляющие ошибки определения координат объекта.

Также отметим, что если для ССН на круговых орбитах параметр ρ (см. формулу (2)) является практически неизменным, то для КА на ВЭО он изменяется в широких пределах, так как зависит от текущей высоты КА.

Возможные конфигурации спутниковых систем наблюдения

В качестве возможных конфигураций ССН рассматривались спутниковые системы на ВЭО типа «Молния». Целевым регионом наблюдений выбрано Северное полушарие Земли. Все рассмотренные конфигурации систем являются однородными — все КА системы имеют одинаковые параметры орбит:

период обращения Т 43 140 с ( ~ 12 ч); высота апогея h _а 38 813,9 км; высота перигея h _π 1 600 км; эксцентриситет е 0,7; критическое наклонение i 63,4 ° ; аргумент перигея w _п 270 ° .

Такие орбиты обладают устойчивостью положения линии апсид по отношению к главному возмущающему члену, связанному с нецентральностью гравитационного поля Земли — её сжатию. Одной из основных трудностей проектирования структур ССН на эллиптических орбитах, в отличие от круговых орбит, является необходимость учёта изменяющегося во времени мгновенного поля обзора КА, зависящего от высоты его полёта. Достоинством же таких ССН является возможность выбора приоритетного района наблюдений при их проектировании. Параметры ССН на ВЭО могут выбираться с учётом локальной стационарности — равенства нулю мгновенной скорости смещения относительно

Земли подспутниковой точки в апогее орбиты [2]. Например, за счёт расположения перигеев в Южном полушарии они обеспечивают хорошие условия для связи и/или наблюдений в целевом регионе — Северном полушарии [3]. Каждая из рассмотренных систем состоит из шести КА на ВЭО — минимально необходимого числа КА для обеспечения постоянного, по крайней мере, однократного покрытия целевого региона.

Путём выбора одинаковых параметров орбит и гринвичских долгот восходящих узлов при проектировании ССН на орбитах типа «Молния» возможно создание так называемых однотрассовых (или одномаршрутных) систем [4]. При сохранении стабильности трасс всех КА в ССН характеристики непрерывного обзора для различных географических областей будут зависеть от прохождения трасс. Таким образом, оптимальное прохождение трассы может быть подобрано для какой-то определённой целевой географической области.

Для представления структуры кинематически правильной системы используется система обозначений [5] в виде тройки целых чисел N / P / F , где N — общее количество КА в системе; Р — количество орбитальных плоскостей; F — фазовый сдвиг положений КА в смежных плоскостях. Последний параметр представляет собой целое число долей 2 п / N .

Всего было проанализировано восемь возможных конфигураций.

Сводные данные по рассмотренным вариантам ССН на ВЭО в соответствии с этими обозначениями представлены в табл. 1.

Таблица 1

Рассмотренные варианты конфигураций спутниковых систем наблюдения

Число спутников N	Число плоскостей P	Фазовый сдвиг F
6	2	0
6	2	1
6	3	0
6	3	1
6	6	1
6	6	2
6	6	3
6	6	4

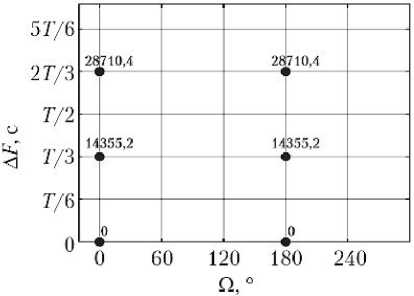
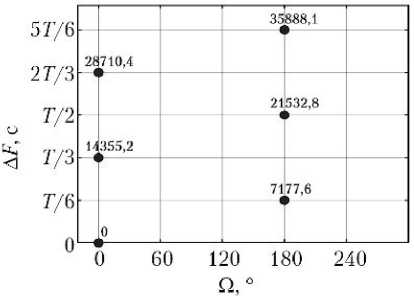
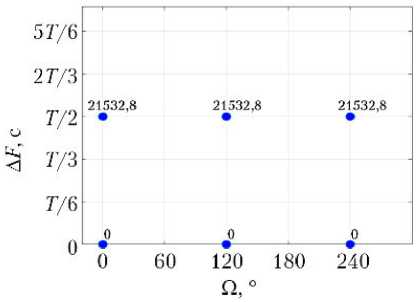
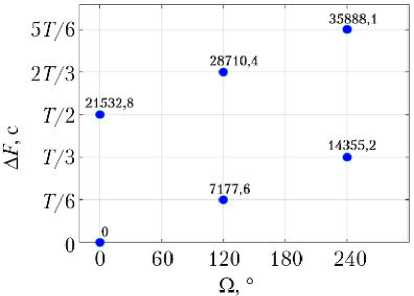
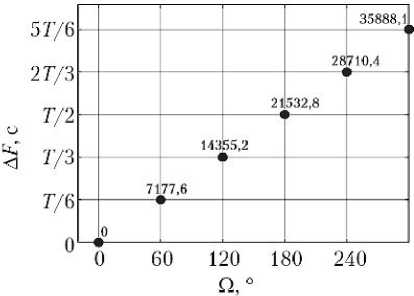
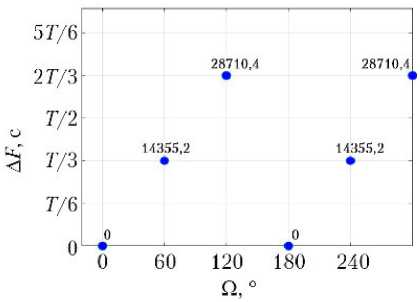
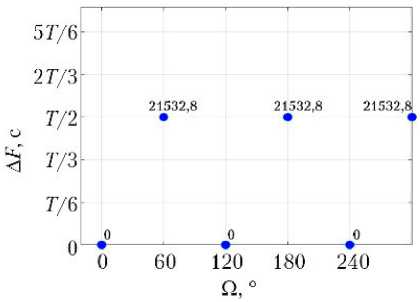
Каждая кинематически правильная ССН может быть представлена в виде равномерно движущейся двумерной решетки [6], отражающей значения инерци- альной долготы восходящего узла Ω и фазового сдвига положений КА ΔF. Конкретные значения Ω и ΔF рассматриваемых вариантов ССН показаны на рис. 2.

а)

б)

в)

г)

д)

е)

ж)

Рис. 2. Значения инерциальной долготы восходящего узла Ω и фазового сдвига положений КА Δ F для спутниковых систем наблюдения: а — 6/2/0; б — 6/2/1; в — 6/3/0; г — 6/3/1; д — 6/6/1; е — 6/6/2; ж — 6/6/3; з — 6/6/4

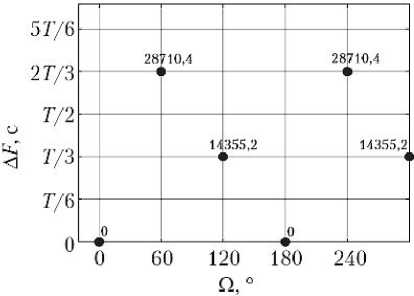
з)

Отметим, что если ССН на круговых орбитах практически не имеют в долговременном масштабе долготной неоднородности, и характеристики точности зависят, в основном, от широты объекта наблюдения, то для эллиптических орбит могут быть получены существенные неоднородности в зависимости от долготы. Для расчётов предполагалось, что все параметры орбит КА в системе удерживаются равными номинальным значениям таким образом, что географические трассы на поверхности Земли остаются неизменными и не дрейфующими с течением времени.

На рис. 3 показан пример построения ССН 6/3/0 и кратность покрытия, обеспечиваемая этой системой.

При расчёте кратности покрытия и всех дальнейших расчётах считалось, что объект на поверхности Земли является видимым для конкретного КА, если попадает в конус ±10 ° от линии визирования, направленной строго в надир. Видно, что система 6/3/0 обеспечивает непрерывное трёхкратное покрытие для широт выше 37 ° с. ш., двукратное — для широт от 20 до 37 ° с. ш. Для широт примерно от 10 ° ю. ш. до 20 ° с. ш. система 6/3/0 обеспечивает лишь однократное гарантированное покрытие. Это означает, что на широтах южнее 20 ° с. ш. погрешность наблюдений будет существенна.

Численное моделирование спутниковых систем наблюдения

Для оценки точностных характеристик ССН по каждой возможной конфигурации проводилось моделирование, учитывающее географическое положение объекта наблюдения. При этом последовательно рассматривались точки поверхности Земли на широте от 0 до 90 ° с. ш. и долготе от -180 до +180 ° с шагом 2 ° . Для каждой рассматриваемой точки проводился прогноз положения ССН на период повторяемости географической трассы на поверхности Земли (для КА на рассматриваемых ВЭО типа «Молния» это 24 ч). В каждый момент времени с шагом 1 мин выделялась горизонтальная погрешность. В сводную таблицу выбирался наихудший вариант, таким образом гарантируя непревышение указанного значения по точности при любых временных и географических (долготных) положениях наблюдателя.

Результаты моделирования показывают, что одним из основных проектнобаллистических параметров, определяющих точность ССН на ВЭО, является способ построения конкретной ССН.

В качестве примера на рис. 4 для ССН 6/3/0 показаны цветные карты изолиний изменения средних ( а ) и максимальных ( б ) погрешностей наблюдений объекта. Численные значения соответствуют шкале цветов, расположенной справа от карт.

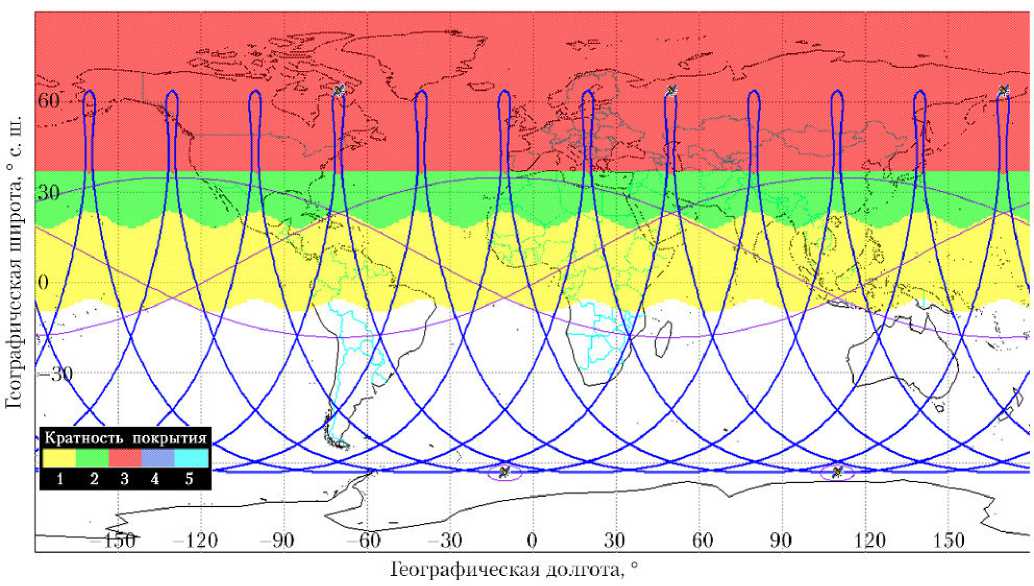
Рис. 3. Пример построения спутниковой системы наблюдения 6/3/0 и кратность покрытия

Для прикладных задач анализа может быть удобно наложение цветовой карты распределения погрешностей на географическую карту местности. Примеры такого наложения средних и максимальных погрешностей для спутниковой системы наблюдения 6/3/0 показаны на рис. 5 и 6, соответственно.

о

Л5                      45                      45

-1э0    -100     50      0      50

Географическая долгота, а)

80 -— 17

60 -

40 ;

20 -

Географ ичеткая долгота,

Видно, что, как и ожидалось, средние и максимальные погрешности значительно увеличиваются при наблюдении широт южнее 20° с. ш. Для широт от 0 до 20° с. ш. погрешности наблюдения имеют существенный разброс, зависящий от конкретных положений КА в ССН, меняющихся во времени. Максимальным значением погрешности, отображаемым на картах, выбрана величина 50 км. Все значе- ния, превышающие этот порог, в графическом анализе были объединены в одну группу.

Также отметим, что, несмотря на высокую кратность покрытия для приполярных широт, обеспечиваемую рассматриваемыми ССН, точность обзора данных районов плавно понижается, начиная с 60 ° с. ш.

4. Изолинии изменения средних (а) и максимальных (б) погрешностей наблюдений

Рис.

объекта для спутниковой системы наблюдения 6/3/0

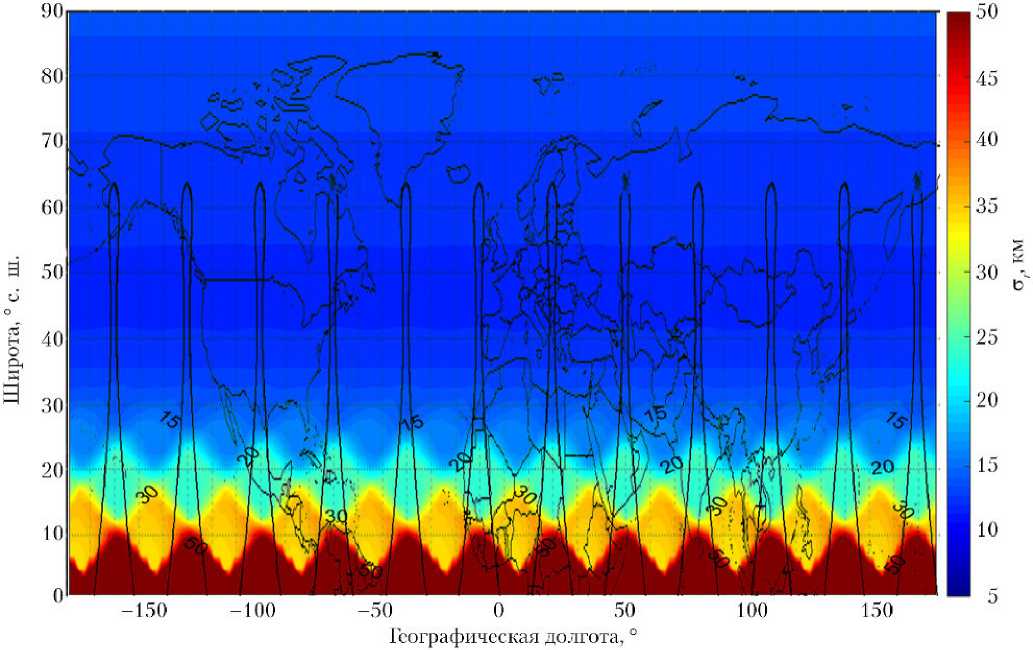
Рис. 5. Наложение цветовой карты распределения средних погрешностей на географическую карту для спутниковой системы наблюдения 6/3/0

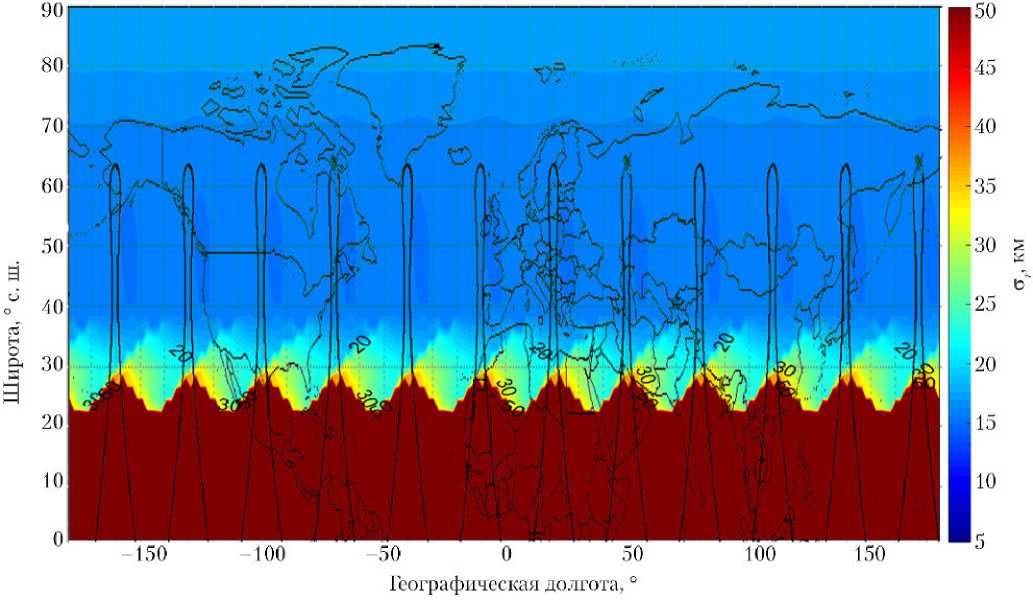
Рис. 6. Наложение цветовой карты распределения для спутниковой системы наблюдения 6/3/0

максимальных погрешностей на географическую карту

Связано это с тем, что в отличие от ССН на круговых орбитах [1], где при постоянной средней высоте КА в системе погрешность наблюдения напрямую зависит от кратности покрытия определённой области (например, для околополярных систем точность наблюдений объекта возрастает с повышением широты объекта, что объясняется повышением кратности обзора), ССН на ВЭО такой прямо пропорциональной зависимости не имеют. Для них точность наблюдения зависит от двух факторов: кратности покрытия и изменяющегося в течение витка расстояния между КА и объектом наблюдения. Таким образом, ухудшение точностных характеристик для высоких широт, несмотря на высокую кратность обзора, связано с существенным увеличением дальности между объектом наблюдения и КА ССН, находящимися в этот момент в околоапогейных районах орбит на максимальной высоте.

На рис. 7 приведён график изменения средней погрешности наблюдений ССН 6/3/0 на различных широтах от 20 до 90 ° с. ш. на долготе 0 ° — синяя линия. Дополнительно на этот же график нанесено изменение среднего значения зависящего от высоты КА параметра р (см. формулу (2)) — красная линия.

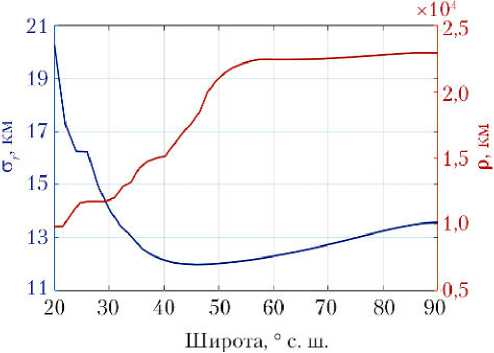
Рис. 7. График изменения средней погрешности наблюдений ( ■ ) и изменение среднего значения параметра р ( ■ ) на различных широтах от 20 до 90 ° с. ш. на долготе 0 ° для ССН 6/3/0

Как видно из рис. 7, погрешность наблюдения коррелирована с расстоянием между КА и объектом наблюдения, но не имеет прямо пропорциональной зависимости.

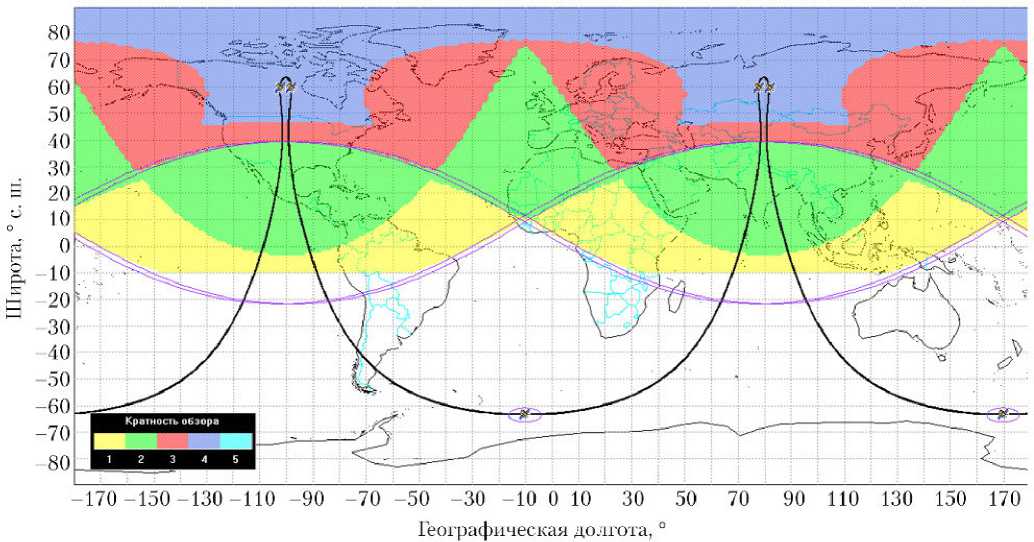
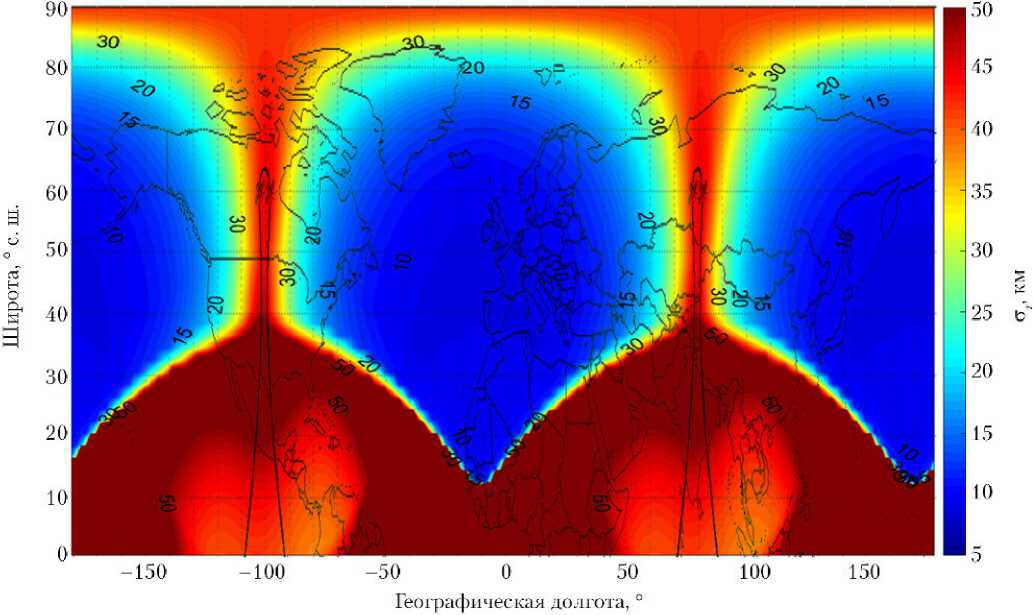
В качестве дополнительного примера рассмотрим ССН 6/6/4. Данная ССН обеспечивает непрерывное трёхкратное покрытие обширных северных регионов, как это показано на рис. 8, а . Однако, погрешности наблюдений для северных широт существенны и достигают 44 км. Карта погрешностей для ССН 6/6/4 показана на рис. 8, б .

а)

б)

Рис. 8. Кратность покрытия (а) и распределение средних погрешностей (б) для ССН 6/6/4

Для улучшения точностных характеристик ССН на ВЭО дополнительно возможно привлечение КА на геостационарных орбитах (ГСО), расположенных в рабочих точках, охватывающих приоритетные районы наблюдений. Пример карты распределения средних погрешностей для ССН 6/3/0 с привлече- нием двух КА на ГСО с долготами стояния ХРТ1 = 0° и ХРТ2 = 90° показан на рис. 9.

Видно, что существенно повысилась точность в приэкваториальных районах в зоне охвата КА на ГСО, а также в районе пересечения зон охвата ГСО по всем широтам.

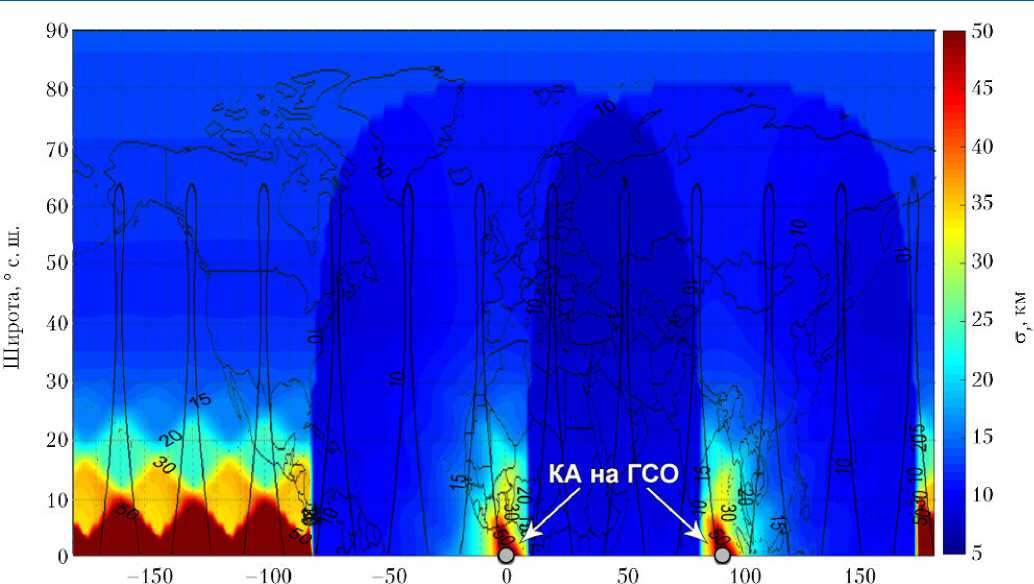
Географическая долгота.

Рис. 9.

Распределение средних

стояния X РТ1 = 0 ° и X РТ2 = 90 °

погрешностей для ССН 6/3/0

с привлечением двух КА

на ГСО с точками

При моделировании оценивались минимальные, средние и максимальные погрешности наблюдения. В табл. 2 приведены значения этих погрешностей при различных вариантах построения ССН.

Так как целевым регионом рассматриваемых ССН является Северное полушарие, то в данную таблицу включались только результаты для широт севернее 20 ° с. ш.

Таблица 2

Широта объекта наблюдений	Тип погрешности	Тип спутниковых систем наблюдения
		6/2/0	6/2/1	6/3/0	6/3/1	6/6/1	6/6/2	6/6/3	6/6/4
20 ° с. ш.	мин.	11,2	9,4	7,177	8,731	12,618	11,038	7,262	47,699
	ср.	—	—	25,845	31,8	—	—	25,112	—
	макс.	—	—	188,184	305,451	—	—	188,184	—
30 ° с. ш.	мин.	9,109	8,247	7,351	8,05	9,863	8,5	7,352	57,665
	ср.	—	18,9	15,502	19,492	—	29,552	15,367	68,775
	макс.	—	122,5	36,816	145,503	—	380,086	31,528	380,08
45 ° с. ш.	мин.	8,181	8,396	6,809	8,3	8,73	7,9	6,844	36,92
	ср.	12,315	11,867	12,074	12,165	12,481	12,652	12,06	46,222
	макс.	50,432	19,1	15,952	22,259	37,909	50,432	15,952	51,173
60 ° с. ш.	мин.	8,609	8,415	6,744	8,161	9,3	8,543	6,716	36,836
	ср.	12,38	11,84	12,226	12,135	11,816	12,608	12,232	44,944
	макс.	57,75	18,268	15,861	21,426	21,249	57,752	15,861	57,752
75 ° с. ш.	мин.	9,804	9,158	6,639	8,802	9,808	10,301	6,632	35,85
	ср.	13,28	12,13	12,828	12,552	11,947	13,804	12,834	43,731
	макс.	64,54	18,647	16,426	20,652	20,558	64,54	16,426	64,54

Значения погрешностей (км) для спутниковых систем наблюдения на высокоэллиптических орбитах для некоторых широт севернее 20° с. ш.

Прочерк в табл. 2 означает, что ССН указанного типа не позволяет постоянно наблюдать объект на данной широте, и, следовательно, максимальная и средняя погрешности не могут быть вычислены. Курсивом отмечены величины, превышающие выбранный порог в 50 км. Жирным шрифтом — наименьшие значения погрешностей данного типа для данной широты.

Из проведённого анализа видно, что оптимальными вариантами построения из рассмотренных ССН являются 6/3/0 и 6/6/3. Такая организация ССН позволяет гарантированно наблюдать объекты, начиная с широты 20 ° с. ш. и севернее. При этом ССН 6/3/0 и 6/6/3 обеспечивают наилучшие точности на всех рассмотренных целевых широтах. Наименьшие средние погрешности при наблюдении широт выше 50 ° с. ш. обеспечивает ССН 6/6/1, однако она не может обеспечить постоянное наблюдение широт от 0 до 40 ° с. ш.

Заключение

В статье приведены оценки погрешностей наблюдения ССН на ВЭО на базе ранее разработанного критерия точности сравнительного анализа многоспутниковых систем непрерывного наблюдения Земли.

Проведённое моделирование возможных конфигураций ССН на ВЭО при различных вариантах построения и для различных географических положений объекта наблюдения показало, что наиболее существенное влияние на точность наблюдений оказывает способ построения конкретной ССН. Также показано, что погрешность наблюдений коррелирована с расстоянием между КА и объектом наблюдения.

Рассмотрен способ повышения точности наблюдений путём привлечения дополнительных КА на ГСО.

Из рассмотренных ССН определены оптимальные с точки зрения минимальных погрешностей наблюдений.

Представленные результаты могут использоваться для предварительного выбора конфигурации ССН на ВЭО.