Сравнительный анализ влияния вида градиентного члена на поведение пластических решений

Ishlinsky Institute for Problems in Mechanics RAS, Moscow, 119526, Russia

The effect of the type of correction functions on the solution behavior is studied within the framework of the theory of gradient plasticity. Two ways of gradient term representation are considered, of which one uses a conventional form, and the other suggests application of space derivatives of the equivalent strain rate. Attention is mainly devoted to the difference in the qualitative behavior of the solutions of the boundary value problem on expansion of a sphere having an inner cavity of small radius acting as a stress concentrator. It is shown that the solution based on the new correction function better corresponds to physical expectations concerning the effect of the gradient term on the solution behavior.

Градиентные теории используются для учета неоднородности напряженного и деформированного состояния в формулировке критериев прочности и пластичности. Обзоры определяющих уравнений градиентных теорий пластичности и обсуждение области применения таких теорий приведены в [1–3]. Основным отличием градиентных теорий пластичности от традиционных является введение градиентного члена (поправочной функции), который содержит пространственные производные инвариантов тензора напряжения [1] или деформации [1–3] . В большинстве случаев объектом исследования при применении градиентных теорий пластичности являются конструкции с концентраторами напряжений или процессы деформирования при малых упругопластических деформациях (см. [4–7]). Однако необходимость учета сильной неоднородности напряженно-деформированного состояния возникает и в процессах развитого пластического течения, например, при обработке материалов давлением (локализация деформаций в операциях листовой штамповки [8]), вблизи поверхностей трения, где наблюдается сильная неоднородность свойств [9]. В частности, для описания процесса локализации деформаций при деформировании листовых материалов одна из градиентных теорий пластичности с градиентным членом, содержащим пространственные производные от накопленной деформации, применяется в [10].

Для описания процессов деформирования при развитых пластических деформациях широкое распространение получили жесткопластические модели, определяющие уравнения которых включают скорости деформаций, а не деформации. Хотя формально эти модели можно дополнить ранее предложенными градиентными членами, содержащими производные от накопленной деформации, представляют интерес качественные особенности решений, вызванные введением этих членов. Необходимо заметить, что ввиду разнообразия формулировок градиентных членов большое значение имеет гипотеза о соответствии вида градиентной поправки виду исходного критерия [1]. С этой точки зрения для жесткопластических моделей градиентный член, включающий производные от инвариантов тензора скорости деформации, предпочтительнее членов, сформулированных по-другому. В некоторых работах пространственные производные от инвариантов тензора скорости деформации вводятся в определяющие соотношения градиентной теории пластичности (например, в [2]). Однако в этих случаях рассматриваются малые упруго-пластические деформации. Скорости деформации определяются как частные производные по времени от соответствующих деформаций, и вследствие этого изменение границ деформируемого тела не учитывается при решении краевых задач.

В данной работе выполняется сравнительный анализ решений модельной задачи о расширении полой сферы при больших пластических деформациях для двух моделей градиентной теории пластичности. Показывается, что при изменяющейся геометрии тела предсказания, основанные на условиях пластичности с градиентным членом, включающим пространственные производные от накопленной деформации, могут не соответствовать общим представлениям о его влиянии на поведение решения.

Исходной для обеих моделей является теория жесткопластического упрочняющегося материала. Определяющие уравнения формулируются в текущей конфигурации для мгновенного напряженно-деформированного состояния. При изложении общих теоретических вопросов принимается (без ограничения общности) декартова система координат. Условие пластичности записывается в виде

° eq = ° 0 ( 1 + ^s eq /^S 0 ) n , ° 0 = const, ^£ 0 = const, ⁿ = const, (1)

где о eq — эквивалентное напряжение и в eq — накопленная деформация, которые определяются из соотношений

° eq = VV² ( ^T j ij ) ¹² , d ^В eql ^t = ⁵ eq .

В этих выражениях T j — девиаторные компоненты тензора напряжения, t — время, 5 _eq — эквивалентная скорость деформации, равная

5„ = 72/3 ( ^ j ^ ₍ j )^V2 _>

и 5 _zj — компоненты тензора скорости деформации. Помимо условия (1), к определяющим уравнениям относится также ассоциированный закон течения

5 j =Xt j , Х> 0.

Обобщенное в работе [11] условие текучести (1) имеет вид:

^ = C0

2 n              ¹²

^{( 1} + = eq /=0 ) + l 0 I Vs eq |      ,

где l ₀ — характерная длина. Очевидно, что критерий (5) сводится к (1) при l ₀ = 0.

По аналогии с (5) вводится обобщение условия текучести (1) в другой форме:

с

( 2 ) eq

= ^С 0

(I + = „/= )2 n + L- V „|

Здесь L ₀ — характерная длина, которая, вообще говоря, отличается от l ₀ ; 4 0 — характерная скорость деформации. В отличие от (5), условие (6) вводит некоторую зависимость сопротивления материала от скорости деформирования. При малых значениях L ₀/4₀ эта зависимость имеет существенное влияние, только если велик градиент эквивалентной скорости деформации, и этим она качественно отличается от подобных зависимостей в общепринятых вязкопластических моделях [12]. Критерий (6) сводится к условию (1) при L 0 = 0 .

Итак, исследуется пластическое течение, возникающее в толстостенном полом сферическом сосуде под действием внутреннего давления p , величина которого должна быть определена из решения краевой задачи. Внутренний a и внешний b радиусы сферы изменяются со временем, а их начальные значения равняются a ₀ и b ₀ соответственно. Скорость изменения внутреннего радиуса сферы задается как a = const.

Вводится сферическая система координат r Оф , начало которой совпадает с центром сферы O , и используются обозначения: нормальные компоненты тензора напряжения — с r , с_О , с_ф ; нормальные компоненты тензора скорости деформации — 4 r , 4₀ , 4_ф ; радиальная скорость — v . В силу симметрии сдвиговые компоненты тензоров напряжения и скорости деформации в сферической системе координат равняются нулю. Кроме того, с_О = с_ф , 4_О = 4_ф и все компоненты вектора скорости, за исключением v , также нулевые. Ненулевые компоненты тензоров напряжения и скорости деформации и радиальная скорость не зависят от углов О и ф .

На внешней и внутренней поверхностях сферы выполняются граничные условия:

с r = 0 при r = b , v = а при r = a .

Уравнение несжимаемости и единственное нетривиальное уравнение равновесия, которые имеют силу для обеих моделей, принимают вид:

d v 2 v

⁺ — = 0, d r r

Sc r . + 2 Cz£ « = 0. d r        r

Для удобства вводятся безразмерные величины:

v

r

и = —, Р = —, a       b0

a = -, ₽ = b , ₽ ₀ = - , X = К a ₀ b ₀ b ₀ a ₀

L_na i

X = _ э .

⁴ 0 ^a 0

Из уравнения (9) с учетом условий (8) и соотношений (11) получается следующая формула для радиальной скорости:

u =

a 2 P 0

P 2

С другой стороны, радиальная скорость может быть записана как v = dr/dt или, с учетом (11), d р/ d a = P ₀ u . Подстановка этого выражения в (12) и интегрирование при начальном условии р = р ₀ при a = 1 задает связь между эйлеровой и лагранжевой координатами:

р ³ -р 0 = ( a ³ - 1 ) Р 0 .                                                                    (13)

В частности, внешний радиус сферы в лагранжевых координатах определяется уравнением р0 = 1, поэтому из (13) следует, что в3 -1 = (a3 - 1)в3.

Это соотношение также может быть найдено непосредственно из уравнения несжимаемости, записанного в интегральной форме.

Компоненты тензора скорости деформации и эквивалентная скорость деформации определяются из формул (3), (11) и (12):

^0 =

a a2p0

р ³

,

^ r =

-2a a2p0

р ³

,

^ eq

2 a a ² p 0 р ³

В лагранжевой системе координат уравнение (2) для накопленной деформации записывается следующим образом: a d£ _eq /д a = L, _eq . После подстановки в это уравнение выражений (13) и (15), с учетом (11), получается:

^д £ eq =      2 a ² p 3

да (a3 - 1)p0 +р0.

Последующее интегрирование при начальном условии £ _eq = 0 и a = 1 позволяет получить распределение накопленной деформации:

^£ eq = 3ln

(al-1)pl + p3 р0

= 2ln — = —ln р о   ³

р ³

^{р 3 -} ( ^a 3 ^- 1 ) ^p 0

Второе и третье равенства в (17) получаются после подстановки выражения (13), связывающего эйлеровы и лагранжевы координаты. В силу независимости накопленной деформации от 0 и ф , величина ее градиента вычисляется по формуле, следующей из (17):

IVe«I = Г[(“3 - O^ + P0Г (“3 - W b0

2 ( a ³ — 1 ) в 0 ^b 0 pp 0

Величина градиента эквивалентной скорости деформации, согласно (15), находится по формуле

IV^ ..| = ^^ [(“3 b

-

1 ) Р 0 +P 0

1 —4/3 _ 6 aa ² p 0

J = bP

Подстановка (17) и (18) в (5), а также (17) и (19) в (6) с учетом (11) приводит к выражениям

^ = °0

<) = °0

1    2 1 P

1 + — ln—

,

■     +

^£ 0 ^p 0 J

2 n

2i P

1 + —ln — v £0 p0 J

2^(«3 - 1)в0

pp 0

,

+

⁶ X ^a P 0

P

.

С учетом уравнения (13) величины c^ и о ( q ) могут быть выражены либо через эйлерову, либо через лагранжеву координату.

В рассматриваемом случае из определения (2) для эквивалентного напряжения следует, что o_o₆-o r . Следовательно, уравнение равновесия (10) с учетом соотношения (11) преобразуется к форме

^ _ 2 °, dP     P

После подстановки в (22) соотношения (20), записанного в эйлеровых координатах, и интегрирования при краевом условии (7) находится распределение радиального напряжения при применении градиентного критерия вида (5):

0L 2(1 ° 0 в x

1 + — ln

^ 0

2n to( x) J

+

2X(a3 - 1)в0

x to( x )3

dx .

Подстановка соотношения (21), записанного в эйлеровых координатах, в уравнение (22) и последующее интегрирование при краевом условии (7) дают распределение радиального напряжения при применении градиентного критерия вида (6)

0 2). _ 2(1 ° 0 i x

1 + — In v    £0

2n x to( x )v

+

⁶ X ^a P 0 x ⁴

dx .

Функция ro ( x ) , входящая в критерии (23) и (24), согласно (13), имеет вид:

w(x) = [x3-(a3 - 1)p0J .

Величина в исключается из выражения (25) с помощью формулы (14). Таким образом, °^ и ° ^{2 )} являются функциями a и р (или р ₀, если величина р выражается через р ₀ в соответствии с (13)). Давление на внутренней поверхности сферы, требуемое для процесса деформирования, следует из (23) и (24) при условии р = ав ₀. Компоненты тензора напряжения °₉ и ° _ф находятся из соотношения

°„ = °.; = ° r + ° eq

° 0    ° 0       ° 0

Отсюда, либо с помощью (5) и (23), либо с помощью (6) и (24), исключаются напряжения о r и ° eq , и далее исследуется влияние безразмерных параметров X и х на распределение напряжений при условии в ₀ = 0,05. Полагается, что параметры материала, входящие в (1), имеют значения: £ 0 = 0,222 и n = 0,25 [13].

Для удобства представления численного решения вводятся величины:

, x      ГТ( 1 )     гт( 0 )

Z(1) = ° r -° r

° 0

, х     гт(²)    г/⁰)

^(2) = ° r — ° r

° 0

, x     ГТ(1) - гт(0)

(1) _ ° 9     ° 9

^Z 9 =

° 0

, X        ( 2 )    rV⁰)

(2) _ ° 9 ^- ° 9

9 "    °0

p ^ = p ⁽¹7 p ^{( 0 )} , p 2 = p ⁽²7 p ^{( 0 )} .

Здесь ° r ^{0 )} и °⁽₉ ⁰⁾ — распределение радиального и окружного напряжения при использовании критерия (1); p ^{( 0 )} , p ^{( 1 )} и p ^{( 2 )} — давление на внутренней поверхности сферы, соответствующее критериям (1), (5) и (6). Очевидно, что Ze ) и Z 9 2 ) характеризуют как распределение напряжения °₉ , так и напряжения ° _ф .

Результаты численного решения уравнений (23)–(27) показаны на рисунках 1–5. При этом части a рисунков отвечают критерию (5) (кривые 1 – 4 соответствуют значениям параметра Х = 0,5; 1; 2; 3), а части б — критерию (6) (кривые 1 - 4 соответствуют значениям параметра х = 0,5; 1; 2; 4).

На рисунке 1 приведены зависимости p ₁ и p ₂ от безразмерного текущего внутреннего радиуса сферы ab ₀ . Из рисунка видна противоположная тенденция в поведении кривых. При использовании условия пластичности в виде (5) с увеличением размера внутренней полости различие между давлениями, рассчитанными по градиентной и традиционной теориям пластичности, увеличивается для всех рассмотренных значений X (Рис. 1, a ). Использование условия пластичности (6) приводит к уменьшению различия между давлениями, так что отношение давлений приближается к единице (Рис. 1, б ). Поскольку по предположению градиентные теории пластичности должны существенно изменять решение вблизи геометрически малых концентраторов напряженно-деформированного состояния, то напрашивается вывод, что критерий (6) более правильно отражает качественное влияние размера внутренней полости на величину давления.

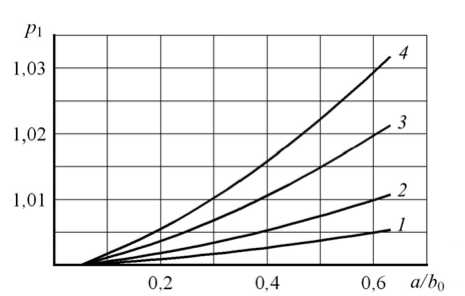
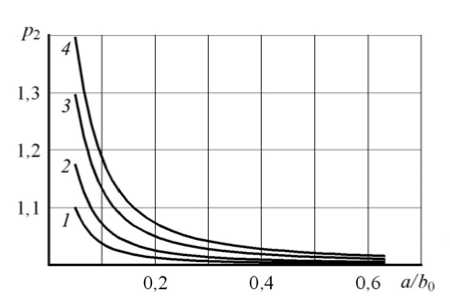
a б

Рис. 1. Зависимость безразмерного давления на внутренней поверхности сферы от текущего значения ее внутреннего радиуса

На рисунке 2 показана зависимость величин Z^ ) и Z r 2 ) от Р в окрестности полости в самом начале процесса ( а = 1,05). Из рисунка видно, что радиальные напряжения, рассчитанные по обеим моделям градиентной пластичности, меньше, чем напряжение, полученное при использовании критерия (1). Однако, если при использовании критерия (6) различие является существенным, то при применении критерия (5) оно незначительно. Необходимо заметить, что в начале процесса геометрический размер концентратора мал, и на этом этапе деформирования эффективнее использование градиентной теории пластичности.

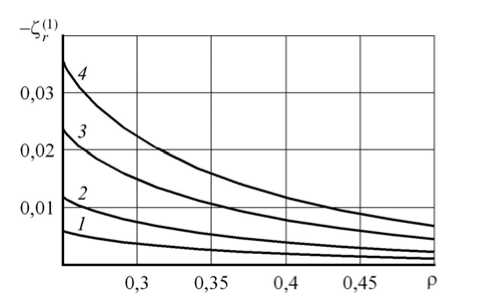
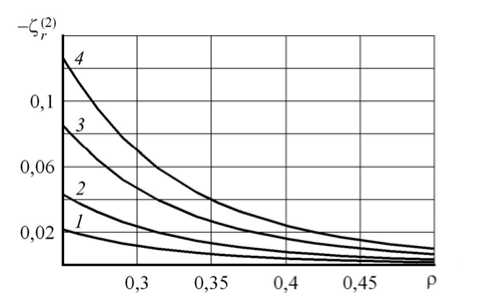
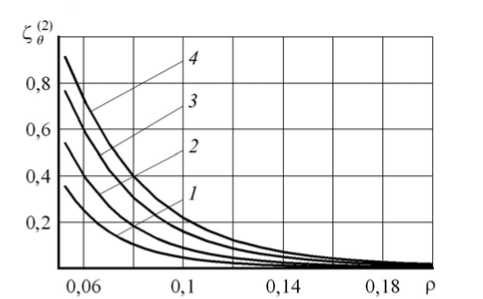
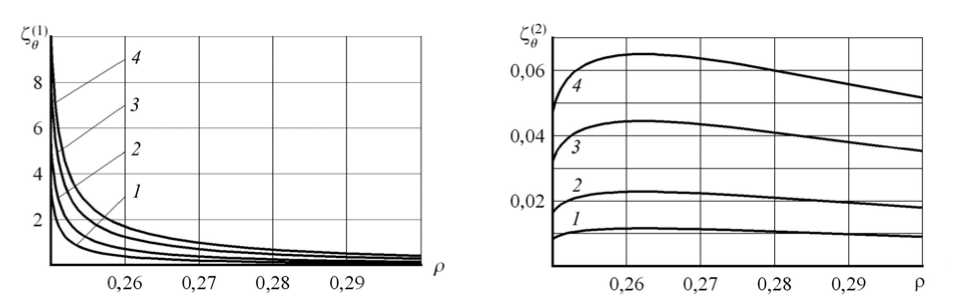
Качественное различие во влиянии критериев (5) и (6) на поведение решения проявляется при сравнении результатов, представленных на рисунке 2, с результатами рисунка 3, на которых зависимость величин Z^ и Z⁽ r 2 ) от Р получена при а = 5 (то есть радиус внутренней полости достаточно велик по сравнению с внешним радиусом сферы: а(Ь * 0,25). Сравнение кривых на рисунках 2, а и 3, а показывает, что различие между решениями по градиентной (5) и традиционной теориям растет с увеличением размера внутренней полости, а при сравнении кривых на рисунках 2, б и 3, б наблюдается противоположная тенденция для градиентной теории пластичности (6). Такой же вывод следует из анализа поведения решений, представленных на рисунках 4 ( а = 1,05) и 5 ( а = 5), демонстрирующих зависимости Ze ) и Z^ 2 от р . Одно из отличий этих распределений от распределений Z^ и Z⁽ r 2 ) состоит в том, что окружные напряжения, найденные по обеим градиентным теориям, больше, чем окружное напряжение, рассчитанное на основе критерия (1). Обращает на себя внимание значительное увеличение окружного напряжения для достаточно больших значений a при применении условия (5) (Рис. 5, a ), что представляется необоснованным. С другой стороны, отличие в величине окружных напряжений, полученных с применением условий (6) и (1), уменьшается с увеличением параметра a (Рис. 4, б и 5, б ) и стремится к нулю. Максимум, который появляется на кривых (Рис. 5, б ), вполне согласуется с качественным поведением других решений вблизи концентраторов напряжений при усложнении определяющих уравнений (например, при использовании упругопластической модели вместо линейно упругой) [14].

Полученные результаты показывают, что при исследовании развитых пластических деформаций со значительными изменениями геометрических размеров концентратора в процессе деформирования модель, основанная на условии пластичности (6), правильнее, чем модель, основанная на условии (5), описывает качественное поведение поля

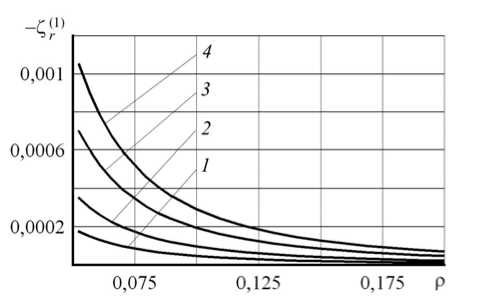
a

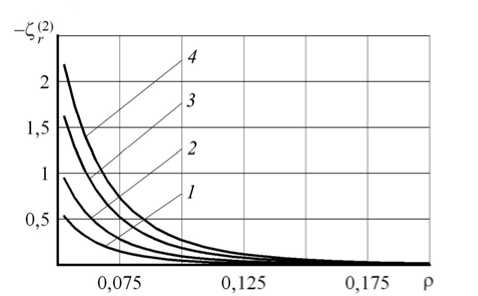
б

Рис. 2. Распределение радиального напряжения в начале процесса деформирования

a                                        б

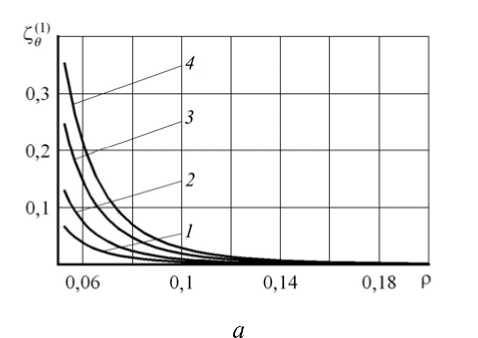
Рис. 4. Распределение окружного напряжения в начале процесса деформирования ( α = 1,05)

Рис. 3. Распределение радиального напряжения при развитых пластических деформациях

б

напряжений, известное из общих представлений о влиянии концентраторов на распределение напряжений вблизи них. Качественное различие в поведении решений связано с качественным отличием в самой формулировке критериев (5) и (6): градиентный член в (5) отражает развитие процесса во времени, а градиентный член в (6) — мгновенное распределение скорости.

Расширение полого сферического сосуда при применении градиентной теории пластичности рассмотрено в [15], где за основную модель принята традиционная теория

а                                          б

Рис. 5. Распределение окружного напряжения при развитых пластических деформациях ( α = 5)

вязкопластичности, а градиентный член задан в виде лапласиана от накопленной деформации. Однако анализ решения ограничен зависимостью давления на внутренней поверхности от коэффициента при градиентном члене. В настоящей работе, в отличие от работы [15], показано, что основной интерес для понимания влияния градиентного члена на характер решения представляют зависимости искомых величин от времени или текущей геометрии процесса.

Работа выполнена при поддержке Российского фонда фундаментальных исследований (проект № 07-08-92113-ГФЕН-а), Совета по грантам Президента РФ для государственной поддержки молодых российских ученых (грант МК-5157.2008.1) и ведущих научных школ (грант НШ-134.2008.1).