Stability Analysis and Evaluation of Soil Cave Foundation under the role of Groundwater in Karst Area

Published Online October 2009 in MECS

Manuscript received January 12, 2009; revised June 21, 2009; accepted July 21, 2009.

Project supported by NSFC (No.40672189)

would impact the stability of the foundation. Currently, the main research is qualitative analysis, few quantitative. Qualitative evaluation is mainly based on the practical experience, which analyzed the character and construction of the soil layer, groundwater, the extent of karst and other factors affecting the stability cave[1~2]. Quantitative evaluation is that the collapse under the stability conditions and according to the test information or collapse factors [3~16].Because of the impact of boundary conditions, the calculation error of the first is larger. And the second is restricted in the practice owing to plentiful test data. In addition, the depth of underground water is one of the main influencing factors which affects the stability of foundation with soil caves, while changes of i t is not considerate in the quantitative evaluation method. According to the statistics in karst region in Guizhou province, more than half of the soil holes collapse has relations to the changes of groundwater. Groundwater leads to the erosion and disintegration of soil. It is also the important influence factor for holes development or collapse. Therefore, the study of soil cave foundation stability under the action of groundwater is particularly important.

After the collapse survey in Tongren prefecture of Guizhou Province, found that many profile shape of the caves are similar to the oval. The damage is from the wall to the surrounding, which leads to the overall instability. At present, the evaluation of the stability is on the assumption that the foundation was overall damaged, and not considered the shape of section, groundwater and others. Practice shows that much of that is damaged by the partial to the overall. Based on the theory of elasticity and plasticity, the stress condition and influence circle of concentration around the cave is researched. And the calculated model of stability of the foundation is found by the method of stress ratio under Mohr-Coulomb strengthcriterion, according to limit equilibrium conditions of soil. The feasibility of the model is proved by the example of the cave foundation in Guizhou province. And research the effect of size and depth of the base of foundation, sectional shape and depth of groundwater to stability to the soil cave foundation. And then expose the formation mechanism of ground subsidence damage from the angle of the quantitatively analysis.

• II.    Stress analysis of soil cave foundation by THEORY OF ELASTICITY AND PLASTICITY

• A. Stress Analysis of Oval Cave

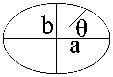
The depth h is the distance from the ground to the oval soil cave, which the semi-major axis is a (horizontal axis) and the semi-minor axis is b (vertical axis). Suppose the soil is homogeneous, isotropic elastic body. According to the theory of elastic and plastic, the stress surrounding the wall in the cave foundation could be equivalent to that of the hole in the unlimited plate which under the condition of bidirectional compression (Figure 1).The vertical stress on the cave is p and the horizontal is q. Because of damage from the wall began, the focus is the size of the tangential stress о у , radial stress о r and shear stress т r _e . According to the complex function of elliptical hole[17], the stress of the point surrounding the cave wall is

2   2         2   22

_c = p [ m ( m + 2) cos 6 - sin 6 ] + q [(2 m + 1)sin 6 - m cos 6 ]

• ⁶                    sin² 6 + m ² cos² 6

(1) and

^C r = ^T r 6 = 0                  ⁽⁴⁾

When m=1, which is a round hole. And the stress of any point around the wall is c6 = p (1 + 2 cos 26) + q (1 - 2 cos 26)    (5)

^C r = ^T r 6 = ⁰

When m =«, which is a vertical fracturing crack. And the stress of any point around the wall is also a constant, which is

c = p ^- q               (7)

^C r = ^T 6 = ⁰

q

^ r = ^T r 6 = ^{0                 (2)}

p

A

B

q

p

Figure 1. Stress distribution in Circular wall

Where о _r , о ₆ , т _r6 is Radial, tangential and shear stress in the surrounding rock, p , q the vertical and horizontal stress on the soil, θ is the eccentric angle of the calculate point, m is the ratio of both elliptical axis, m=b/a (shaft angle).

When m=0, which is a horizontal tension crack. And the stress of any point around the wall is a constant, which is

c = q - P              (3)

According to the standpoint of stability, the stability can be determined by the maximal stress, more than the strength of the soil. From the research, we can see the maximal stress on the surrounding of the elliptical hole in the horizontal axis (6=0, n) and the vertical axis (9=л/2, 3n/2). From (1), we get when the original stress (p, q) is fixed value, the size of the tangential stress, о6, changed by the ratio of the elliptical axis, m.

B. Analyse of Stress State in Wall Rock of Soil Cave

Generally, the size of oval soil cave in engineering is not too big, the affected area for concentration of stresses simplify to the around of hole. There is a rectangular plate, a small hole with a radius of a in the more distant away from the border, in the all four sides of the uniform distribution pull of the p. Through the analysis of elasticity, the original question can be transformed into a new problem: with an inner radius of outer radius of b, the outer boundary of p, the stress of the circle or cylinder is [18]

^ r

C T

b 2 p

b ²

a ²

b2p b2 - a2

(1 - a^ ) r

a ²

(1 + —) r

^T r 6 = ^T6 r = ⁰                   (11)

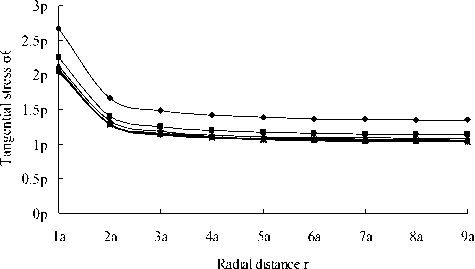
From (9) to (11), we can see that the radial stress or and tangential stress о6 changes with the radial distance r and the sheet size of b. The trends can be seen in the figure 2 and 3.

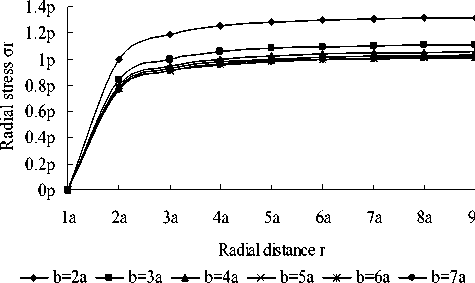
Figure 2. The radial stress distribution chart

P = aAP0 + ^CA

q = X(aBP + Hcb )

Where, α A and α B are the additional stress coefficient of the basement to A (6=n/2), B (6=0) points; P₀ is additional stress of the basement; σ CA and σ CB are the self-weight stress of geotechnical point A and B ; λ is pressure coefficient of the soil.

When the pressure at the bottom of the foundation

loads in large area: a_A = 1, a_B ^ 1,then

p = aP + Gca

q = z( p0 + Gcb )

b=2a b=3a b=4a b=5a b=6a b=7a

Figure 3. The tangential stress distribution chart

p=p0+σCA

AB

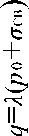
From figure 2 and 3, nearby the hole, tangential stress о_в is largest with radial stress о r = 0 and shear stress т r _e =0.With the increase of r , о r and o_e trend to the original soil stress p. When b>> a, r = 6a , о r = 0.97p , o_e= 1.03p, and the original stress error is only 3%. From the view point of engineering, it is acceptable. So it can be considered for its impact radius R = 6a. So it is 6 times of the impact radius in the elastomer that the influencing region of the stress concentration of the surrounding of hole.

Therefore, as long as the length from the bottom of soil cave foundation to the center of soil cave h> 6a (a is radius of soil, vertical length of semi-minor axis of oval cave), we can use (1) and (2) to solve the stress distribution around soil cave.

Because foundation size is not infinite, i.e. basal pressure range is limited, it can be treated as follows: out of circle scope for 6a in diameter, is still using elastic mechanics of elasticity theory about half of the space, namely regular foundation of additional stress calculation method, and separately calculated additional stress α A P 0 of point A and α B P 0 of point B which is 6a away from the hole center. α_AP₀ and α_BP₀ (Figure 4),can be approximately used for additional stress on level surface of A and vertical surface of B.

Therefore, with the building loads, the foundation soil stress around the hole is:

I I I I

Figure 4. Stress calculation of soil cave foundation

• A.    Improvement of Stability Evaluation Model on Cave Foundation

From the foregoing, we can see that in the oval soil cave wall, o r = 0 , т_гв= 0 , o_e is not only effected by p, q, but also the value of θ and m. When p, q given, σ θ changes with m and θ . The maximal stress are two points about the direction of (θ = 0, π) and the minimum stress on the floor and crest of soil cave. Therefore, when evaluating the stability of the cave, it is important to evaluate the stability of the key point. If it was not damaged, it could be considered the soil cave is stable; on the contrary, destructed.

According to the geometric relationships of tangent of stress and shear strength round lines (Figure 5), a point of the soil shear failure can be expressed by о 1 and о 3 from Mohr-Coulomb strength criteria establish, that is the limit balance conditions of soil [19]

71 = 73 tan2 (45 + -2) + 2c tan( 45 + -2) (14)

or

73 = 71 tan 2 (45 - --) - 2c tan( 45 - ---) (15)

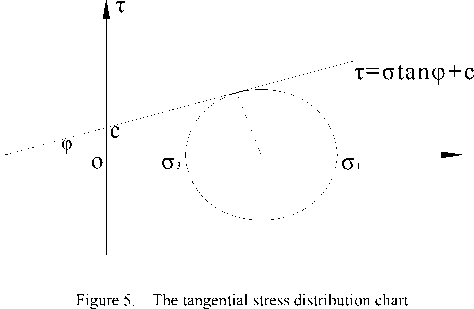
In the soil cave wall, as τ rθ =0, σ θ , is the largest principal stress while σ _r minimum, that σ₁=σ _θ , σ ₃ =σ _r =0. From soil limit equilibrium conditions, we get that

7_g<7 1 = 7 r tan²(45 + - /2) + 2 c tan(45 + - /2)         Safe

• 7_e = 7 1 = 7 r tan²(45 + - /2) + 2 c tan(45 + - /2) Limit - equilibrim

7_g >7 1 = 7 _r tan²(45 + - /2) + 2 c tan(45 + - /2)         Fail

The limit equilibrium conditions can be judged the state of equilibrium of any point in the soil, but it could not assess its stability. To determine quantitative evaluation of the stability of soil cave foundation, the authors suggested adapt stress ratio approach to get the quantitative evaluation of the stability of soil cave foundation, that is, the stability factor for soil cave foundation is

7 _r tan² (45 + ^- ) + 2 c tan( 45 + ^- )

K =   = ----------²------------2-

⁷ g                  ⁷ g

Where σ₁ can be seen as anti-soil cave collapse stress, which is determined by the minimum stress and shear strength of soil, σ θ can be regarded as collapse stress. When K>1.0, the soil cave foundation is soil stable; while K=1.0 that is in the limit equilibrium state; when K <1.0, that is of instability.

From the analysis by 2.2, we can see that applicable conditions of the calculation method of stability are as follows: the length from the bottom of soil cave foundation to the center of soil cave h >6 a ( a is the radius of soil, vertical length of semi-minor axis of oval cave). From (1), (12), (13) and (17), we get that the main factors that have an impact on soil cave foundation are:

additional stress, self-weight stress, water pressure and parameters of shear strength of the geotechnical. While the additional stress is determined by the basis size, depth and number of the basement additional stress; self-weight stress is affected by the weight of the soil, and the depth of the groundwater.

• B.    Plastic Boundary of Holes Damage Area

When the p Ap plastic boundary around the hole soil is rule less. It is hard to get the exact boundaries of plastic zone. At present, there is no solution, usually approximate calculation method for determination of plastic zone boundaries. Its principle is find soil stress around the hole at first according to the elastic theory, then use plastic conditions. Regions where conditions were satisfied are called plastic zone. This method can only approximate to plastic zone boundaries, but the stress of the plastic zone. Specific solutions are as follows:

Determine the stress σ r , σ θ , τ rθ at some point surrounding the circular holes according to (1); If the hole for elliptic, use (5); If the hole for the other shape, determine the stress at key point.

According to σ r , σ θ , τ rθ at some point, accepts largest principal stress σ 1 and minimum principal stress σ 3 .

7 g + 7 r | 7 1 = 2 ^A	( 7 g - 7 r ) 2 2      + T r g
7 g + 7r _ 7 3     2 V	( 7 g - 7 r ) 2 2      + T r g

Finally, the obtained largest principal stress σ 1 and minimum principal stress σ 3 can be judged by the mohr-coulomb criterion.. Plastic failure zone is a region which is formed by a series of damage points .

• A.    Stability Analysis of Soil Cave Foundation

A comprehensive office building, near Liangshuijing along Dongtai Road in northwest of Tongren, was built by Tongren Administration of Taxation. At present, there are some partial land subsidence damages in the building. In the project area, the soil consists of light yellow and hard plastic-like red clay with the average thickness of 9.6m , and the bedrock mainly consists of light grey, thinlayered and moderate weathered limestone. The 2.0 × 2.0m² independent foundation under column is going to be adopted in the project. The basis depth is 2.0m , groundwater is a diving at the depth of 3.0m , the bearing capacity of hard plastic red clay is 230 kPa , clay weight Y= 18.2kN/m³, saturated clay weight Y sat = 18.7kN/m³ , c= 53 kPa, ф= 28°, basement additional stress P 0 = 120 kPa . There is an oval soil cave with semi-major axis a = 0.3m and short half axis b = 0.25m under 5.0m of foundation. There are no fillings in the soil cave, and lateral pressure coefficient λ= 0.5 . According to analysis in section 2, the impact radius of stress concentration is 1.5m, and the computing model is shown in Figure 6.

Surface

Foundation шшшп к 2.0m

TABLE II.      T he stress results in surrounding soil

θ	σ θ ( kPa )	σ r ( kpa )
0°	292.4	40
15°	272.5	40
30°	223.6	40
45°	167.3	40
60°	120.3	40
75°	90.5	40
90°	80.4	40

Red clay

p

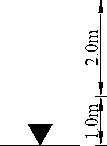
0.6m

q

^q

Soil cave

^p

3.0m

Figure 6. Computing modal on soil cave foundation

In order to obtain the stress around the soil cave, we firstly obtain the vertical and horizontal force p , q from 6a of soil cave centre. After calculated, the parameters which are required by (12) and (13) are

α A = 0.10075, α B = 0.0604.

σ CA = 18.2×3.0+(18.7-10)×2.5=76.35 kPa

σ CB = 18.2×3.0+(18.7-10)×4.0=89.4 kPa

From (12) and (13), we can obtain p =88.44 kPa , q =48.324 kPa . Taking them into (1) and (2), we can obtain the stress around the soil cave, which are σ r =0, τ r θ =0. The results are different, as σ θ is in the different position of soil cave. Since the oval soil cave is a plane axial symmetry problem, we only calculate 1/4 part of it. The tangential stress results are shown in Table I.

TABLE I.

T he tangential stress results in surrounding soil

θ	σ θ ( kPa )
0°	252.4
15°	232.5
30°	183.6
45°	127.3
60°	80.3
75°	50.5
90°	40.4

As groundwater is a diving at the depth of 3.0 m , the soil cave is in the hydrostatic pressure state. The hydrostatic pressure, P_w=γ_wh_w= 40 kPa . Consequently, the radial stress σ _r and the circumferential stress σ_θ around the soil cave should be added to the hydrostatic pressure P w = 40 kPa , the ultimate results are shown in table II.

As shown in table II, the maximum stress (θ=0) around the soil cave are σ θ = 292.4 kPa, σ r = 40 kPa. From (14) we can calculate the maximum principal stress (collapse stress) around the soil cave is σ 1 = 287.2 kPa. t aking above results into (17) , we calculate the stability factor of soil cave foundation, K=0.982<1.0, so the soil cave foundation is instable in the maximum stress state. Therefore, the soil cave foundation is overall instable. As the results of stability calculation are consistent with the surface investigation, the stability of evaluation methods which is established in this paper is feasible in the evaluation of stability of soil cave foundation.

• B.    Mechanism of Collapse and Stability Analysis

• a.    Basis size on the stability of soil cave

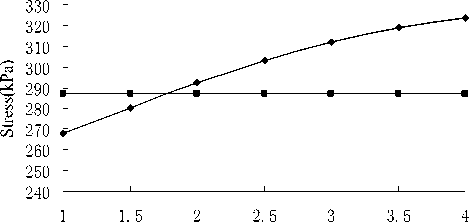
To study the basis size on the stability of soil cave, we assume that, the basis size (square) gradually increases from 1.0m to 4.0 m, and the other conditions (including basement pressure p, etc) are unchanged. The stability of soil-curve is shown in figure 7 and figure 8.

Basis size(m)

—collapse stress —■— ant-collapse stress

Figure 7. Basis size on the stability of soil-curve

Basis size(m)

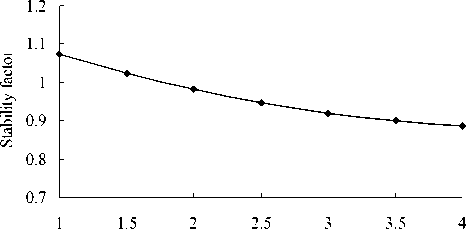
Figure 8. Stability factory changes with basis size

According to figure 7 and figure 8, when basis size gradually increases from 1.0m to 4.0m and the other conditions are unchanged, collapse stress rises rapidly, and ant-collapse stress remains unchanged. Consequently, the stability of soil cave is significantly reduced. It shows that it has a great impact on the stability. The basis size is smaller, the foundation is more stable. As known from the limit equilibrium conditions (K=1.0 or σ1=σθ), the maximum is 1.8 m, rather than the actual is 2.0 m. So the foundation collapsed probably due to the larger designed size, leading to the collapse stress in the cave is more than the ant-collapse.

• b.    Basis depth on the stability of soil cave

0.5    1    1.5   2   2.5    3   3.5   4   4.5   5

To study the basis depth on the stability, we assume that, the depth gradually increases from 0.5m to 5.0 m, and the remaining conditions are unchanged. The influence is shown in figure 9 and figure 10.

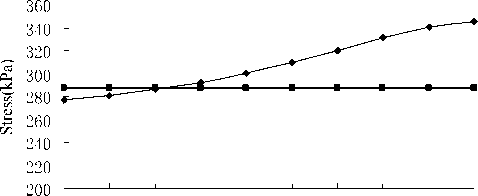
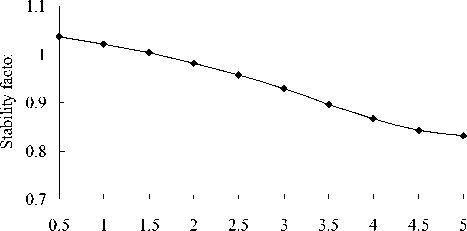
According to figure 9 and figure 10, when the depth gradually increases from 0.5m to 5.0m and the remaining conditions are unchanged, collapse stress rises rapidly, and ant-collapse remains unchanged. Consequently, the stability is significantly reduced. It shows that the depth has a great impact on the stability. That is shallower, the foundation is more stable. As known from the limit equilibrium conditions ( K =1.0 or σ₁=σ_θ), the critical depth (maximum depth) is 1.75m, rather than the actual is 2.0m. So foundation collapsed probably due to the too deep designed depth, resulted the collapse stress in the soil cave is more than the ant-collapse.

Basis depth(m)

—♦— collapse stress —■— ant-collapse stress

Figure 9. Basis depth on the stability of soil-curve

Basis depth ( m )

Figure 10. Stability factory changes with basis depth

• c.    The effect of cave shape on the stavility

0 0.2 0.4 0.6 0.8   1   1.2 1.4 1.6 1.8   2

In order to study the effect of cave shape on the stability, in this project, other conditions were invariable, and b which stands for semi-minor axis (vertical axis) was invariable, namely influencing radius was invariable. As depicted in figure 11 and figure 12, elliptic axial ratio gradually increased from 0.2 to 2.0, stress effect change curve of soil shape on the stability of soil-curve was obtained by calculating.

As depicted in figure 11 and figure 12, when elliptic axial ratio gradually increased from 0.2 to 2.0, and other condition was all invariable, the collapse stress decreased apparently, anti-collapse stress was invariable, the stability increased sharply, it showed that the shape of soil cave had great influence on stability, the cave was more stable while the ratio of vertical axis b and horizontal axis a was higher.

5 400

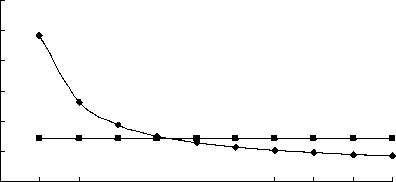
Elliptic axial ration

♦ collapse stress —■— ant-collapse stress

Figure 11. Basis shape on the stability of soil-curve

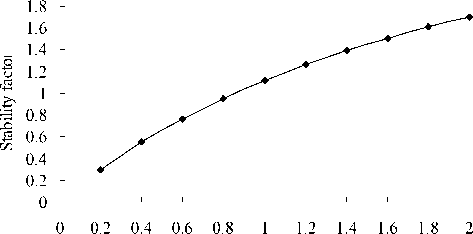
Elliptic axial ration

Figure 12. Stability factory changes with basis shape

• d.    The effect of depth of groundwater on the stability

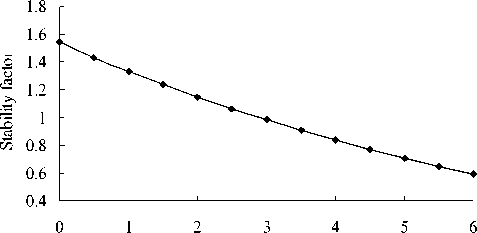
In order to study the effect of the depth of groundwater on the stability, in this project, other condition was all invariable; the depth of groundwater was increased from 0m to 6.0m. As shown in figure 13 and figure 14, groundwater on the stability was obtained by calculation.

As depicted in figure 13 and figure 14, when the depth of groundwater gradually increased from 0m to 6.0m, and other condition was all invariable, the collapse stress increased and anti-collapse’s decreased in uniform speed, the stability decreased sharply. It showed that the depth of groundwater had great influence on the stability. It was good for the stability of foundation, when the depth of groundwater was shallower. The descending within a narrow range may change the stable soil cave into failure one. According to limit equilibrium condition (K=1.0 or σ1=σθ), the maximum depth of the groundwater is 2.89m, but the actual depth is 3.0m, hence the cause of foundation failure of this cave is that excessive pumping of groundwater which induce the decrease of it and make it exceed the critical level, then surface subsidence occurs.

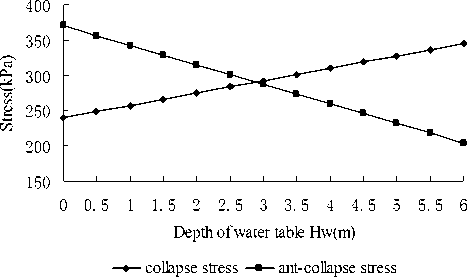
Figure 13. Groundwater on the stability of soil-curve

Depth of water table Hw(m)

Figure 14. Stability factory changes with groundwater

Ⅴ . CONCLUSIONS

For soil cave foundation, the stress around the cave will be concentrated under the effect of self-weight stress and additional stress. According to the method that was deduced by elastic theory, as long as the distance, between bottom of the foundation and centre of the soil cave, h>6a (a stands for the radius of rotundity or the vertical semi-minor axis of elliptical), the stress distribution of soil cave foundation would be solved by the method of solving it of the hole in infinite plate that under two-way pressure.

The calculated model of stability of the foundation, which is quantitative evaluation, is found by the method of stress ratio under Mohr-Coulomb strength-criterion combined with soil body limit equilibrium condition according to the stress state around the soil cave wall.

Taking the soil cave foundation in Tongren, Guizhou province for example, using the calculated method, the stability factor of the foundation was 0.982, in unstable condition. That was consistent with the actual surface survey, so the calculation model was feasible. And the maximal size of the foundation is 1.8m, the depth is 1.75m, the maximal depth of the groundwater is 2.89m, which could play an instructive role in the prevention and design of soil cave foundation.

By analyzing of the influence factors, gained that the collapsed stress is higher as larger, deeper of the foundation, smaller of the elliptic axial ratio, m, deeper of the groundwater, conversely smaller. The resisting stress is lower as deeper of the groundwater, the only factor. And the influence of the groundwater is sensitivity, which the cave would fail at the groundwater declining in small amplitude. Therefore, attention shall be paid to the quantitative analysis on the soil cave, especially affected by groundwater.

This paper is supported by the National Natural Science Foundation of China (NO.40672189), and is also supported by China University of Geosciences (Wuhan) Graduate Academic Exploration and Innovation Foundation(Key Supporting Program: NO.CUGYJS0705).

• [1]    Qunli Dai. Formation mechanism and preventive of Karst collapse. China Coalfield Geology, 1994,6(2):59-63.

• [2]    Zhiqing Wan,Siqing Qin,Zhigang Li,Haitao Qian. Formation mechanism and initial condition of soil cavity.Chinese Journal of Rock Mechanics and Engineering, 2003,22(8):1377-1382.

• [3]    The compile commission of geological engineering manual geological engineering manual .3rd edition. Beijing: The Architectural Industrial Publishing House of China, 1992.

• [4]    Bin Li, Qiuyan Fan, Fengrong Qin.Analysis on roof stability of kaest cave in karst areas. Chinese Journal of Rock Mechanics and Engineering, 2002,21(4):532-536.

• [5]    Keqiang He, Bin Wang, Jitao Wan. Study on Forming Mechanism Of Zaozhuang Karst Collapse and Collapse Model. Rock and Soil Mechanics,2002,(5): 564-569.

• [6]    Zhikui Liu, Jincheng Liang, Jianghong Zhou. Analysis of formation mechanism of soil caves in caves karstic. Journal of Engineering Geology, 2004,12(1):45-49.

• [7]    Jianpu Zhou, Xianmin Li. Methods of stability analysis in karst foundation.Mining and metallurgical engineering, 2003,23(1):4-8.

• [8]    Zhikui Liu.Study on effect of cave and cave soil on building foundaton in karst region .the Doctoral Thesis in Central South University, 2004.

• [9]    Quanwu Wang.Caverns soil-stability evaluation and project treatment, Gansu Science and Technology, 23(6):175-178.

• [10]    Charles w w Ng,Pang.Y.W.Influence of state on Soil ～ water Characteristics and slop stability.Journal of Geotechnical and Geoenvironmental Engineering,2000, 126(2):157 ～ 166.

• [11]    G.Sevket Koruc ， Birol Elevli. Blasting practices in a quarry with karstic cavities. Journal of University of Science and Technology Beijing, 2002,9(6):406 ～ 411.

• [12]    Liu Zhikui,Liang Jincheng,Zhu Shouzeng.Stability analysis of soil cave foundation in karst area.Hydrogeology and Engineering Geology,2003,3:24 ～ 28.

• [13]    Honggui Liu, Jianda Liu,Hangang Xu.Crosshole ultrasonic tomography and its application to karst investigation.Acta Seismologica Sinica,2003,16(4):441 ～ 448

• [14]    Roth, M.J. S;Mackey, J.R.; Mackey, C.; Nyquist, J.E.,. A case study of the reliability of multielectrode earth resistivity testing for geotechnical investigations in karst terrains, Engineering Geology, Aug2002, Vol. 65 Issue 2/3, p225, 8p.

• [15]    Cooley T.Geological and geotechnical confext of cover collapse and subsidence in mid-continent US clay-mantied Krast.Environmental Geology, 2002 ， 42:469 ～ 475.

• [16]    Kaiming Tian, Fusheng Hu, Li Wan. Discontinuous flow of fracture water:a new technique of karst collapse prevention,Environmental Geology,October 2001,Volume 40, Numbers 11 Pages: 1347 ～ 1352

• [17]    Bingye Xu,Yan Huang, Xinsheng Liu, Xuewei Sun.The mechanics of elasticity and plasticity and its application . Beijing: Mechanic Industrial Publishing House, 1984.R. Nicole, “Title of paper with only first word capitalized,” J. Name Stand. Abbrev., in press.

• [18]    Jihong Bi,Hui Wang.Elasto-plastic mechanical engineering. Tianjin:Tianjin University Press,2003.M.Young,The Technical Writer's Handbook. Mill Valley, CA: University Science, 1989.

• [19]    Zhongyi Chen, Jingxing Zhou. Soil Mechanics. Beijing: Qinghua University Press, 2002.

  
  
  

  E’chuan Yan was born in Mianyang , Sichuan province in 1969, and earned bachelor degree, master degree and doctor degree in geological engineering in Chengdu University of Technology in China respectively in 1990, 1995 and 1998,

and is still studying in this field now. Dr. Yan is deputy director of Youth Committee of Engineering Geology in China, and association for Engineering Geology of Hubei Province. And he was awarded the leader of the subject of geotechnical engineering in China University of Geosciences in Wuhan.

He has worked for 2 years after undergraduate from 1990 to 1992 at Northwest Geological Team in Sichuan, and was a teacher in ChengDu University of Technology from 1995 to 1999, and was a post-doctoral and associate professor in China University of Geosciences in Wuhan from 1999 to 2001 and became a professor in 2003. He was a doctoral advisor in 2005 and continued to work on education in China University of Geosciences in Wuhan from then on. During this period he also cooperated with Hong Kong, Switzerland, Leica Geosystems Ltd in 2001 at the study of the monitoring of Landslide disaster.

In 2005, got the title of “excellent instructor” in the 9th challenge cup university student extracurricular academic science and technology activities, "excellent teacher" in the sixth youth science, "excellent head teacher ", China university of geosciences 7th"ten outstanding youth" and so on. He took part in 30 projects or tasks since 1995, 3 of them are still on study and the rest were completed.

Since 1997, more than 34 papers or articles were published in the domestic and foreign public journals, including six papers for EI and ISTP retrieval. Other two articles won prizes：one article got the first prize for 2000, Chinese academy of sciences journal papers, the other got outstanding prize for 2002 the second national post-doctoral geological academic seminar . major writings includes: principles and applications numerical modeling in engineering geology( second author), the evaluation and utilization of engineering stability (the first author). Three achievements obtained provincial rewards , a scientific and technological progress first prize awarded by Henan provincial water resources bureau, a scientific research achievements third prize in geology (ministry of land and resources), another for 2003 science and technology progress first prize of Hubei province. In November 2001, won first prizes of youth research group in China university of geosciences 。2008 got thesilver hammer prize。 his major writings includes: principles and applications numerical modeling in engineering geology(Wuhan, China: press of China University of Geosciences, 2001 ,second author), the evaluation and utilization of engineering stability (Wuhan, China: press of China University of Geosciences, 2002,the first author). He has high attainments in landslide. He mainly engages in scientific research and teaching work on engineering geology, geotechnical engineering and environmental geological. Now he makes researches on geological hazard and geotechnical engineering design and evaluation on environmental protection and prevention. He especially does well in numerical modeling in engineering geology.

Jiangtao Cheng was born in Yingcheng ， Hubei province in 1983, and earned bachelor degree, master degree in geological engineering in China University of Geosciences in 2006, 2008, and now is a doctor student.

Li Liu was born in Jingzhou ,Hubei province in 1984, and earned bachelor degree, master degree in geological engineering in China University of Geosciences in 2006, 2008.