Стационарная и колебательная конвекция бидисперсной коллоидной суспензии

Конвективные процессы в молекулярных смесях осложняются диффузионным и термодиффузионным транспортом примеси [1, 2]. В коллоидных растворах, где размеры наночастиц на несколько порядков больше характерного размера молекул, может добавиться оседание примеси в гравитационном поле [3, 4] либо магнитофорез феррочастиц в неоднородном магнитном поле [5]. Эти процессы влияют на перераспределение примеси, открывают возможность для возникновения колебательной конвекции, сказываются на эволюции нелинейных течений [6–12]. Отметим, что в [8] колебательная конвекция коллоидной суспензии (магнитной жидкости на основе керосина) рассматривается в рамках модели трехкомпонентной смеси, состоящей из двухкомпонентной жидкости-носителя, которая в результате термодиффузии может разделяться на компоненты, и монодисперсных наночастиц, оседающих под воздействием гравитационного поля.

Несмотря на то что реальные суспензии полидисперсны [13], для описания конвекции в коллоидных растворах (наножидкостях) или в магнитных жидкостях часто используется монодисперсная модель [10–12]. Однако в некоторых случаях монодисперсная модель не достаточна для корректного представления

коллоидной суспензии. Тогда применяется так называемая бидисперсная модель, в которой считается, что в однородной жидкости-носителе содержится два типа наночастиц, разнящихся только своими размерами (условно говоря, малые и большие наночастицы). Эта модель дает хорошее согласование с экспериментом [14].

Результаты исследования конвективной устойчивости бидисперсной коллоидной суспензии относительно длинноволновых и ячеистых возмущений представлены в [15], где показано, что существуют длинноволновые колебательные возмущения с большим периодом и ячеистые колебательные возмущения. Вследствие эволюции колебательных возмущений в бинарных смесях и коллоидных суспензиях возникают разнообразные нелинейные режимы конвекции: протяженные и локализованные состояния, активно изучаемые экспериментально [7–9], теоретически [5, 10, 11] и с посредством численного моделирования [12, 17].

В данной статье рассматривается трехкомпонентная смесь (бидисперсная коллоидная суспензия), которая качественно отличается от обсуждаемой в [8]: здесь оба типа компонентов (большие и малые наночастицы) переносятся благодаря диффузионному, термодиффузионному и конвективному транспорту, а также участвуют в гравитационном оседании. На основе численного моделирования анализируется конвекция коллоидной суспензии, заполняющей горизонтальный слой. Построена бифуркационная диаграмма, где отражены решения в виде стационарной конвекции и бегущих волн, а также получены распределения гидродинамических и концентрационных полей компонентов смеси.

2.    Постановка задачи и метод решения

Рассмотрим горизонтальный слой коллоидной суспензии толщиной h , находящийся в поле силы тяжести g . Ось x декартовой системы координат направим вдоль нижней границы слоя, а ось z поперек слоя. Твердые непроницаемые идеально теплопроводные границы слоя имеют координаты z =± h) 2. На этих границах поддерживаются некоторые фиксированные температуры: T ( h/ 2 ) = T u , T ( - h /2 ) = T u +0 , где при имеющем место нагреве снизу 0 >  0.

В рамках бидисперсной модели будем считать, что коллоидная суспензия содержит две фракции наночастиц: маленькие (радиусом r s ) и большие (радиусом r l = a r s , а> 1). Средние массовые доли малых ( C_s ) и больших ( C_l ) наночастиц связаны со средней массовой долей образуемых ими «тяжелой» примеси ( C = C_s + C l ) соотношением:

C l =Y C ,    C s = ( 1 -y) C ,                                     (1)

где y — доля больших наночастиц. Считаем, что коэффициенты диффузии частиц обоих типов D i ( i = s , l ), а также температуропроводность х и вязкость п суспензии постоянны.

Представим уравнение состояния смеси в виде:

р=р ₀ ( 1 - р _г 0+р s Z s +P l Z I ) ,    Z s = C s - C s ,    Z 1 = C l - C l ,                        (2)

где p ₀ — плотность коллоидной суспензии при некоторой средней температуре T и средних массовых концентрациях C_s , C l , при этом 0 и Z _s , Z i — отклонения температуры и концентрации от своих средних значений, в T , р i — коэффициенты теплового и концентрационного расширения компонентов ( i = s , l ) (в силу одинаковости материала больших и малых частиц их коэффициенты концентрационного расширения являются равными: р _s = P _l ).

Введем безразмерные масштабы длины — h , времени — h ²/х, скорости жидкости — х/ h , температуры — 0 , давления — р ₀ % ² [h ² и концентраций — C i =P0/P _T . Запишем систему уравнений конвекции коллоидной суспензии:

• V- v = 0,

dv + (vV) v = -Vp + Pr Av + PrRа (0-Z s -Z l) e = 0,—+ (vV)0 = A0,                                     (3)

^ + ( v V ) Z i = Le i V

V(Z,.+Vi0) + ZLe , xi _

i = s , l .

Система (3) содержит: t — время; p — давление; V и A — стандартные дифференциальные операторы; e — единичный вектор, направленный вверх; безразмерные числа Прандтля Pr = v/х и Релея

Ra = (в Tgh 3®)/(v%) ; параметры, которые характеризуют компоненты коллоидной суспензии, относящиеся к малым (i = s) и большим (i = l) наночастицам — числа Льюиса Lei = Djx; безразмерные длины седиментации       X, = h](Xsed). ,      где

( X sed ) = к Б Т /( Ap gV i ) ;

параметры разделения

V i = ( S t ) i С , ( 1 - q)( P i /p T ) , где ( S _t ). — коэффициенты термодиффузии компонентов; к_Б — постоянная

Больцмана, Ap — разность плотностей наночастиц и жидкости-носителя, V i — объемы наночастиц.

Решение системы (3) должно удовлетворять закону сохранения массы. Для каждого из компонентов смеси запишем это требование в безразмерной форме:

J C s dz =

- 12

B s X s

Rа

J C l dz =

- 1/2

B I X I Rа

При этом появляются дополнительные параметры

числа Больцмана B i = P i gh⁴C i /( v% ( X _sed ) i )

для каждого компонента ( i = s , l ).

Граничные условия на вертикальных границах области зададим периодическими с периодом L = 2, на горизонтальных границах — соответствующими твердым изотермическим непроницаемым для примеси границам:

z = ± 1:    v = 0 ,    ^ + у—+ Ci- = 0 ,    9 ( - 1/2 ) = 1,    9 ( 1/2 ) = 0 .

2                d z    i д z X i                          м )

Периоду L = 2 отвечает волновое число к = 2л/ L = п , согласующееся с критическим волновым числом возникновения конвекции при нагреве жидкости снизу:

F ( x , z , t ) = F ( x + L , z , t ) ,                                            (6)

где F — любая из функций системы (3).

В общем случае параметры, характеризующие малые и большие наночастицы, можно записать в виде соотношений, включающих отношение радиусов а = r l/ r_s и коэффициент у* 0 , показывающий долю крупных частиц:

Le i = Le _$ /а , X , =X _$ /а ³ , B _$ = ( 1 -у ) B, B_t = yа ³B , у s = ( 1 -y ) v , у i =«W •    (7)

Здесь B = P s gh^4C /( v% ( ^X sed ) _s ) и у ( C ) — число Больцмана и параметр разделения монодисперсной жидкости определяются через концентрацию «тяжелой» примеси C . При расчетах использовались следующие значения: у = 0,1; а = 2,5 ; Pr = 10 ; Le _s = 1,5 - 10 ^{- 4}; X _s = 30 ; B = 2000 ; у _s = 1,8; у l = 0,5 .

Нейтральная кривая, разделяющая области растущих и затухающих возмущений основного состояния, полученная в результате решения краевой задачи с помощью метода ортогонализации, представлена на рисунке 1. Нейтральная кривая имеет два локальных минимума: в длинноволновой области при Ка ( к = 0 ) = 2142 и в области ячеистых возмущений при Ка_osc ( к = 3,14 ) = 2006 . Абсолютный минимум на нейтральной кривой концентрации связан с ячеистыми колебательными возмущениями при волновом числе к = 3,14 и частоте ® = 8,173. С уменьшением волнового числа частота нейтральных возмущений убывает (Табл.).

Фактически речь идет о двух разных колебательных модах. Для первого типа возмущений (интервал D–G на Рис. 1) квадрат частоты линейно зависит от суммы чисел Больцмана, но не зависит от чисел Льюиса [15]. Такие колебания связаны с тем, что насыщенный наночастицами, но нагретый элемент суспензии всплывает в более холодную область с меньшей концентрацией. В результате охлаждения этого элемента он становится более тяжелым, чем его окружение и тонет, попадая в более нагретую жидкость. Далее процесс повторяется.

Для второго типа колебаний (интервал B–D на Рис. 1) существенным моментом является зависимость конвективной скорости от концентрации обеих компонент (малых и больших наночастиц), а их эволюция в длинноволновом пределе определяется диффузией (числами Льюиса, которые экстремально малы) [15]. Квадрат частоты для этого типа колебательных возмущений зависит от чисел Льюиса.

Для анализа эволюции нелинейных течений введем функцию тока Ψ и завихренность Φ , связанные со скоростью жидкости v соотношениями:

5^

vx =^" ,   vz =— ,   Ф=( rot v )z • dzd

И перепишем систему уравнений (3) для моделирования двумерных течений с учетом введенных

параметров:

дФ  Г д с дФ  д Т дФ1  „ '  „ „ f д"   dZs  dZ/^1 += Pr АФ + Ra 11 ,     А Т = Ф ,              (9) 1 д t   <д z д x   д x д z J [        \д x   д x   д x )_ д" Г д Т д" д Т д0П 6 t +V0 z 0 x"ax . .     '"•                                       19)2 &Т ^ -гт^ 1=^+(       Le vrv(Ci+Vi")+C i . J ,    , . s , , .        (9) 3 д t . д z д x    д x д z J д t V ’         ‘ [ V i ‘ ’ X i J

Тогда условия на горизонтальных границах примут вид:

1              д Т                 де1     д" C i z = — : Т = 0,   — = 0,    0 = 1,-- + w j --1--= 0, 2              д z                д z      д z X i _ 1    Ш       д Т               дZ i     д" C j                       10 z = — : Т = 0,   — = 0,    0 = 0,-- + w +--= 0, 2                д z                 д z      д z  X i

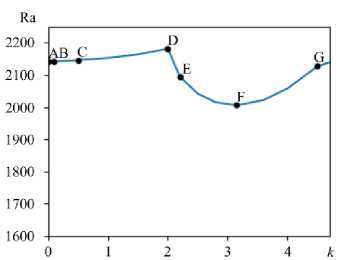
Рис. 1. Нейтральная кривая конвективной неустойчивости бидисперсной коллоидной суспензии при заданных значениях параметров компонентов

Таблица. Характеристики возмущений в фиксированных точках нейтральной кривой (Рис. 1)

Точка на нейтральной кривой	к = 3,14	Ra osc	to
A	0	2142	0
B	0,1	2142	0,000086
C	0,50	2146	0,00094
D	2,00	2183	0,00886
E	2,20	2095	3,36
F	3,14	2006	8,173
G	4,50	2127	3,5

а для завихренности Ф поставим условия Тома [18]: на вертикальных границах функции Т ( x , z , t ) , Ф ( x , z , t ) , " ( x , z , t ) , Z j ( x , z , t ) , Z l ( x , z , t ) удовлетворяют условиям периодичности вида (6).

В качестве начальных условий воспользуемся значениями полей, характеризующих состояние механического равновесия [15]:

Т(x, z, t = 0) = 0, Ф(x, z, t = 0) = 0, "(x, z, t = 0) = 1/2-z, CGZ,-O1-Bxlx-fB^.-„L  ,-sl                       (11) е x, z, t                                  w z,           j , , i                 Ra ( Ra     ) с возмущением конечной амплитуды для завихренности в двух фиксированных точках:

Ф ( x = L /4, z = 1/2, t = 0 ) = - 1,    Ф ( x = 3 L 4, z = 1/2, t = 0 ) = 1.                 (12)

Для получения решений в подкритической области Rа <  Rа_osc применим метод продолжения по параметру.

При численном моделировании нелинейной стадии конвекции строилась сетка 128 x 64. Пространственные производные в уравнении движения (9) 1 и в уравнении теплопроводности (9) 2 аппроксимировались центральными разностями. Конечно-разностная аппроксимация уравнений для концентрации (9) 3 должна удовлетворять закону сохранения массы. Это достигалось путем консервативной формы записи уравнения и аппроксимации его при помощи метода контрольного объема [19]. Решение уравнения Пуассона для функции тока на каждом шаге по времени проводилось с использованием быстрых преобразований Фурье [20].

Далее анализировались как локальные, так и интегральные характеристики системы. Основной исследуемой функцией являлась функция тока Ψ . Рассматривались ее максимальное значение внутри ячейки в текущий момент времени: Т_max ( t ) = max |^Т ij ( t_k ) J , и значение в фиксированной точке ячейки: Т_1ос ( t ) = Т ( 0,5 ;0,5; t k ) . В фиксированной точке ячейки также определялся Фурье-спектр колебаний функции тока Ψ_loc .

3.    Переходные и устойчивые режимы конвекции коллоидной суспензии

При расчете методом конечных разностей для ячейки длиной L = 2л/ к = 2 , соответствующей критическим возмущениям, граница устойчивости механического равновесия (Conductive State — CS) соотносится с Ка osc = 2035. От предсказанного линейной теорией в предыдущем разделе результата

Ка osc = 2006 отклонение составляет 1,3%. Частота колебаний на начальном участке течения равняется ® = 6,66 (отклонение от значения, найденного согласно линейной теории 18,5%). Эволюция возмущений при Ка = 2050, представленная на рисунке 2, свидетельствует, что конвекция в коллоидной суспензии возникает вследствие обратной бифуркации Хопфа. Уже при небольшой надкритичности (0,7%) максимальное значение функции тока в конвективной ячейке принимает конечное значение: T max = 1,69 .

Этап I ↓

Этап II ↓

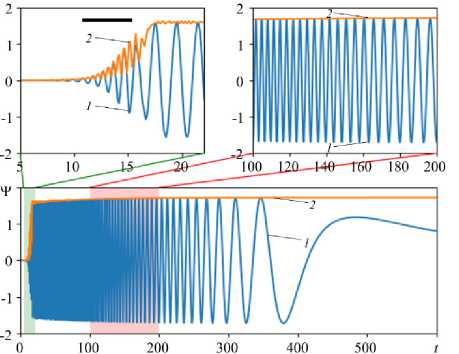
Рис. 2. Эволюция функции тока в фиксированной точке конвективной ячейки T loc ( t ) (линия 1 ) и максимального значения функции тока Т t (линия 2 ); Ка = 2050 max

На этапе I (0 <  t <  12) осциллирует и растет по амплитуде не только значение функции тока в локальной точке T_loc ( t ) , но и ее максимальное значение T_max ( t ) . Такое поведение решения свидетельствует о том, что течение представляет собой стоячую волну (SW), амплитуда которой постоянно растет. Затем, на этапе II (12 <  t <  19), как в случае бинарных молекулярных смесей [16] или коллоидных суспензий [10, 11], в результате спонтанного нарушения симметрии режим стоячей волны переходит в режим бегущей волны (Traveling Wave —TW).

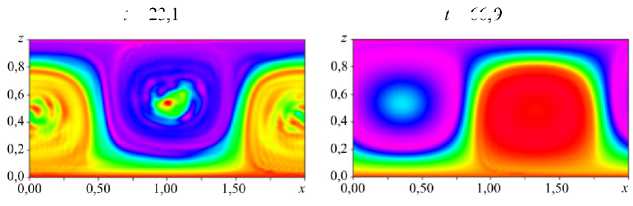
Эволюция поля концентрации больших наночастиц во время перехода от SW к TW представлена на рисунке 3. Видно, что в режиме стоячей волны имеется зеркальная симметрия решения относительно плоскости, проходящей через середину ячейки ( t = 16,1). В следующий момент ( t = 18,3) жидкость поднимается в центре ячейки

(при x = 1,0 ) и опускается по ее краям (при x = 0 и

x = 2). Зеркальная симметрия решения нарушена: вихрь,

вращающийся по часовой стрелке (с центром в x = 1,5) захватывает большее количество тяжелых частиц из нижнего приграничного слоя и легкой, обедненной частицами суспензии, из верхнего приграничного слоя, чем противоположно вращающийся вихрь (с центром в x = 0,5). Далее ( t = 18,8) направление вращения конвективных вихрей и течение в центре конвективной ячейки меняются на противоположные, но максимум модуля конвективной скорости отвечает той же координате: x = 1,0. В дальнейшем появляется горизонтальное движение. При ( t >  20, Рис. 3) поле распределения примеси качественно перестраивается, появляются узкие погранслои, разделяющие области с высокой и низкой концентрацией примеси.

t = 16,1

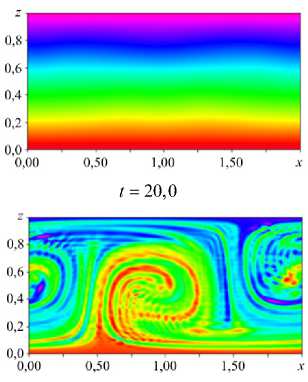
t = 18,3

t = 18,8

t = 23,1

t = 66,9

Рис. 3. Распределение полей концентраций больших наночастиц при переходе от стоячей волны к бегущей; Ка = 2050

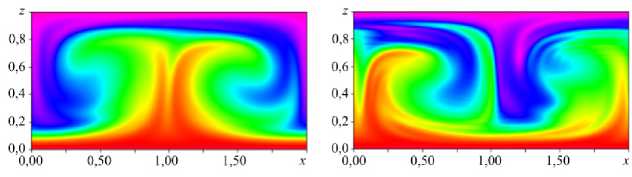
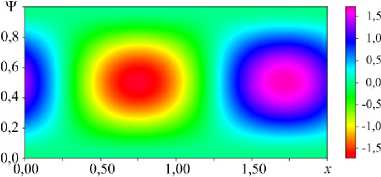
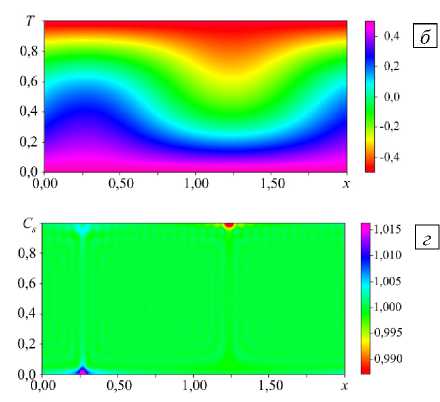
Последующая эволюция бегущей волны в бинарной коллоидной суспензии отличается от поведения в монодисперсной среде [10, 11]. На завершающейся довольно продолжительной части перехода к финальному состоянию (Рис. 2, 17 <  t <  600) период колебаний функции тока в фиксированной точке постепенно увеличивается, конвективная структура (бегущая волна) при этом замедляется до полной остановки. Последний максимум T loc ( t = 475 ) значительно меньше У max ( t ) (см. Рис. 2), что говорит об остановке бегущей волны. Термодиффузионный и гравитационный транспорты не могут поддерживать значительные концентрационные неоднородности. Частота и фазовая скорость бегущей волны уменьшаются до нуля, и в слое устанавливается стационарная конвекция (Stationary Overturning Convection — SOC). Длительность переходного процесса, например, для полимерных частиц в слое h = 0,29 см составляет ~10 час. Поля функции тока, температуры и концентраций малых и больших частиц в режиме SOC представлены на рисунке 4.

а

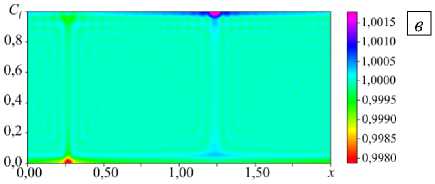
Рис. 4. Распределение полей функции тока ( а ), температуры Ra = 2000

( б ) и концентраций малых ( в ) и больших ( г ) наночастиц;

Поле функции тока и поле температуры демонстрируют слабый пространственный ангармонизм: ведущей в разложениях по горизонтальной координате является первая пространственная гармоника. При этом поля концентрации малых и больших наночастиц имеют качественно иной вид, а именно: распределения примеси внутри конвективных валов практически однородны. Небольшие области неоднородности располагаются вблизи горизонтальных границ в застойных областях между конвективными валиками, где скорость перемешивания стремится к нулю. Отметим, что максимум распределения малых частиц соответствует минимуму распределения крупных частиц. Это можно объяснить тем, что рассматривается случай положительной термодиффузии. Под действием градиента температуры и большие, и малые наночастицы движутся в более холодную область (к верхней границе), причем из-за разницы в параметрах термодиффузии ( ^ _$ = 1,8, ^ l = 0,5) параметр разделения и термодиффузионный градиент

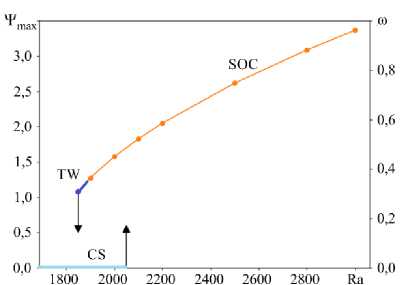
Рис. 5. Бифуркационная диаграмма конвективных течений бидисперсной коллоидной суспензии

малых наночастиц более чем в три раза превышают значения для больших наночастиц. Гравитационное оседание приводит к транспорту наночастиц в обратную сторону (к нижней границе). Но если для малых наночастиц результирующий поток направлен к холодной верхней границе, то для крупных наночастиц гравитационное оседание доминирует над термодиффузионным потоком, и частицы собираются у нижней границы.

Бифуркационная диаграмма решений, характеризующих состояние бидисперсной коллоидной суспензии представлена на рисунке 5. При Ка >  Ка osc = 2035 неустойчивость наступает колебательным образом, однако после длительного переходного процесса устанавливается режим SOC.

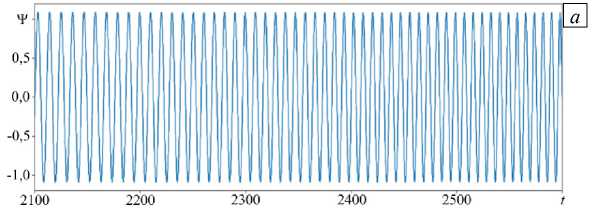
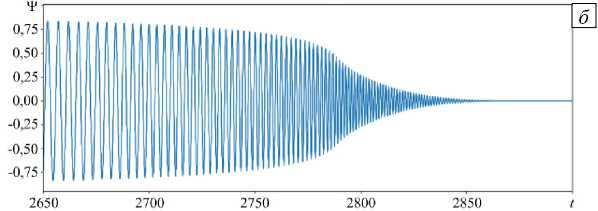
Рис. 6. Эволюция во времени локальной функции тока в режиме бегущей волны ( а ) и в переходном режиме от бегущей волны к равновесному состоянию ( б )

Как и в случае бинарной смеси, будем обозначать границу между режимами TW и SOC как Ra* ® 1875. В исследуемом течении Ra* < Raosc. Дальнейшее уменьшение числа Релея приводит к тому, что в области Ra TW < Ra < Ra* реализуется устойчивый режим бегущей волны (Ra » 1850 , Рис. 6а). В интервале 2400 < t < 2600 значение функции тока в локальной точке осциллирует с постоянной частотой ш = 0,785 . Далее, при Ra < RaTW = 1825 , режим бегущей волны становится неустойчивым (Ra = 1800 , Рис. 6б). Сначала амплитуда течения и конвективный перенос медленно уменьшаются, затем наступает фаза быстрого спада амплитуды течения, и увеличения частоты колебаний до значения ш = 4,99. Возмущения становятся малыми и затухают.

Бидисперсная коллоидная суспензия переходит в состояние механического равновесия (CS).

4.    Заключение

На основе бидисперсной модели, предполагающей наличие малых и больших наночастиц, численно исследована нелинейная стадия конвекции коллоидной суспензии в нагреваемом снизу горизонтальном слое. Получены характеристики переходных и конвективных устойчивых течений: бегущей волны и стационарной конвекции. Параметры суспензии таковы, что под действием гравитационной седиментации тяжелые наночастицы накапливаются у нагретой нижней границы, откуда вымываются конвективным течением. Выявлены условия существования протяженных состояний: стоячих и бегущих волн, а также стационарной конвекции. При превышении числом Релея критического значения в слое возникает колебательная конвекция в виде стоячей волны. Как и в случае монодисперсной коллоидной суспензии, эта стоячая волна оказывается неустойчивой. Следующий за ее распадом длительный переходный процесс завершается формированием режима стационарной конвекции. Поля концентрации малых и больших наночастиц в этом режиме практически везде однородны, за исключением застойных областей между конвективными валами вблизи горизонтальных границ, где наблюдаются небольшие неоднородности. В подкритической области обнаружен устойчивый режим бегущих волн. Построена бифуркационная диаграмма конвекции коллоидной суспензии. Получены зависимости максимальной функции тока и частоты колебаний в волновых режимах.

Исследования выполнены при финансовой поддержке Российского фонда фундаментальных исследований (проект № 20-01-00491).