Станок с параллельными приводами координатных перемещений рабочего органа

Подавляющее большинство металлообрабатывающих станков, промышленных роботов и других манипуляционных машин имеют последовательную кинематическую структуру. Их выходное звено (суппорт, стол, схват) связано со стойкой (станиной) единственной кинематической цепью, которая является разомкнутой. Перемещение выходного звена по нескольким координатам достигается за счет использования соответствующего числа приводов, включенных в указанную кинематическую цепь последовательно. Примером может служить трехкоординатный фрезерный станок консольного типа с ЧПУ, разомкнутая кинематическая цепь которого состоит из одного неподвижного звена (станины) и трех подвижных звеньев - консоли, поперечных салазок и стола. Перечисленные звенья образуют три поступательные пары, имеющие приводы, которые обеспечивают перемещение заготовки, установленной на столе, вдоль трех осей декартовой прямоугольной системы координат.

Приводы и направляющие поперечных салазок и стола, размещенные на консоли, существенно увеличивают ее совокупную массу, что отрицательно сказывается на динамических показателях станка и увеличивает его материалоемкость.

В то же время известны механизмы с параллельными приводами, у которых несколько приводов (как правило, линейных) перемещают одно и тоже выходное звено. Такими механизмами являются платформы Гауфа и Стюарта, манипулятор Данилевского и другие [1]. Платформа Стюарта соединена с основанием шестью стержнями изменяемой длины. Каждый стержень состоит из двух звеньев, образующих поступательную пару, и привода линейных перемещений. Шесть верхних шарниров, с помощью которых стержни соединяются платформой, являются сферическими (трехосевыми), шесть нижних, соединяющих стержни с основанием, являются двухосевыми (кардановыми).

Согласованно изменяя длины шести стержней, можно осуществлять движение платформы по шести координатам (трем линейным и трем угловым). При заторможенных приводах подобные механизмы обращаются в пространственные фермы, стержни которых благодаря шарнирным соединениям воспринимают только осевые нагрузки, чем обеспечивается высокая жесткость механизма при малой материалоемкости. Масса подвижных звеньев в подобных механизмах существенно меньше суммарной массы подвижных звеньев в механизмах последовательной кинематической структуры.

Однако в механизмах параллельной кинематической структуры, в отличие от предыдущих, работа одного привода приводит к перемещению выходного звена одновременно по нескольким координатам. Покажем это, рассмотрев простейший плоский механизм, изображенный на рис. 1. Выходным звеном механизма является планшайба 1, центр которой (точка А) может перемещаться по двум координатам - х и у. Угловая координата pz планшайбы может быть либо произвольной (там, где это допустимо), либо остается постоянной за счет дополнительной (пассивной) кинематической цепи 2 в виде двух параллелограммов. Механизм имеет два линейных привода, изменяющих длины стержней АВ и АС. При работе одного привода, изменяющего, например, длину стержня АВ, точка А будет перемещаться по окружности с центром в точке С, т. е. будут изменяться обе ее координаты - х и у. Механизм имеет особые положения, при которых оба стержня расположены на прямой ВС. Передаточные отношения от каждого привода до выходного звена по обеим координатам - непостоянны.

Указанные особенности механизмов с параллельными приводами свидетельствуют о том, что управление движением выходного звена этих механизмов представляет намного более сложную задачу по сравнению с управлением механизмами последовательной кинематической структуры, в которых каждый провод перемещает выходное звено только по одной координате.

Однако с появлением и развитием микропроцессорных систем управления и научных основ мехатроники задачи управления движением выходного звена механизмов с параллельными приводами стали вполне разрешимыми, что и вызвало практический интерес к таким механизмам и появление станков-гексаподов с шестью управляемыми координатами [2].

Наряду с преимуществами (малой материалоемкостью и хорошими динамическими выше вели-отли- свойствами) эти станки обладают и недостатками. Главными из них являются отмеченные сложность управления и наличие особых положений, а также недостаточные жесткость и чины перемещений по некоторым координатам.

Рассматриваемая ниже кинематическая схема станка-гексапода (рис. 2) существенно

чается от традиционной для этого класса станков схемы платформы Стюарта и имеют перед ней, на взгляд автора, определенные преимущества.

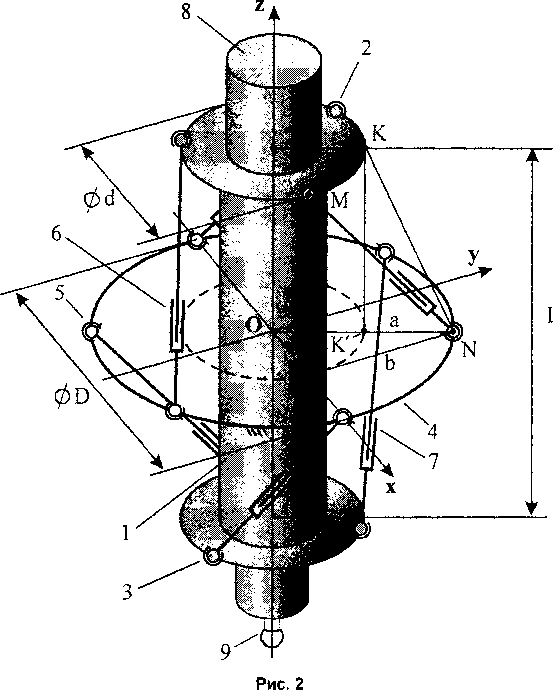
Исполнительным органом станка является гильза 1. На верхнем и нижнем торцах гильзы расположены сферические шарниры 2 и 3, по три шарнира на каждом торце. Центры шарниров каждого торца расположены на окружностях с интервалом 120°, а между собой две группы сферических шарниров смещены на 60°. На неподвижном основании 4 равномерно расположены шесть двухосных (кардановых) шарниров 5, которые соединены стержнями 6 и 7 изменяемой длины с шарнирами 2 и 3, расположенными на торцах гильзы 1. Шарниры верхней и нижней групп стержней на основании 4 чередуются. В гильзе 1 расположен вращающийся от электродвигателя 8 шпиндель с закрепленным в нем инструментом 9.

Удлиняя по одному и тому же закону все нижние стержни и соответственно укорачивая верхние, можно вертикально опускать гильзу 1. При этом силовая нагрузка на инструмент воспринимается всеми шестью приводами стержней равномерно.

Изменяя по периодическому закону длины всех стержней со смещением по фазе на 60°, можно осуществлять движение оси гильзы по поверхности прямого кругового цилиндра с вертикальной осью.

Изменяя длины верхних стержней по периодическому закону со смещением по фазе на 60°, а длины противоположных им нижних стержней в противофазе, можно осуществлять движение оси гильзы по поверхности прямого кругового конуса. Более сложные алгоритмы изменения длин стержней позволяют перемещать ось гильзы по весьма сложным траекториям.

Реактивный момент на статоре электродвигателя 8 воспринимается всеми шестью стержнями, поскольку поворот гильзы под действием реактивного момента вокруг своей оси при неизменных длинах всех стержней возможен только при смещении ее фланцев с шарнирами 2 и 3 навстречу друг другу. Поскольку фланцы соединены жесткой гильзой 1, то такой поворот возможен только в пределах, обусловленных упругой деформацией всех стержней, работающих на растяжение или сжатие. Это обеспечивает достаточную жесткость механизма по координате pz (см. рис. 2).

Управление поворотом гильзы вокруг своей оси имеет свои особенности. Во-первых, при обработке вращающимися (от электродвигателя 8) инструментами (сверлами, фрезами, шлифовальными кругами и т. п.) такое движение гильзы не требуется. Однако при закреплении на гиль- зе некоторых видов схватов и измерительных головок оно должно быть предусмотрено. Поворот гильзы вокруг своей оси достигается одновременным уменьшением или увеличением длин всех шести стержней. При этом следует иметь ввиду то обстоятельство, что некоторые из положений механизма по отношению к координате pz являются особыми. При особых положениях гильзы все стержни располагаются в плоскостях, проходящих через ось гильзы и центр своего неподвижного шарнира. Механизм становится неуправляемым по координате фг . Поэтому необходим, например, дополнительный привод для выведения механизма из особых положений, либо эти по

ложения должны быть запрещены.

Рассматриваемый механизм имеет пять основных геометрических параметров: D - диаметр окружности расположения центров неподвижных шарниров; d - диаметр окружностей расположения центров подвижных шарниров; L -длина гильзы (расстояние между плоскостями расположения подвижных шарниров; /mjn, /шах - минимальная и максимальная длина каждого из шести стержней.

При этом параметры d и /шт, как правило, определяются конструктивно - из условий размещения шарниров на фланцах гильзы и на нижних частях стержней. Для аналитического определения остальных из названных параметров необходимо задать величины желаемых перемещений гильзы (параметры рабочей зоны станка) и составить необходимые соотношения.

Введем неподвижную правую прямоугольную систему координат станка Oxyz, координатная плос

кость хОу которой совпадает с плоскостью расположения центров неподвижных шарниров, а на

чало координат - с центром окружности (диаметром D), на которой они расположены (см. рис. 2).

Примем, что в исходном положении ось гильзы совпадает с осью Oz, а плоскость хОу делит длину гильзы пополам. Проекции всех шести стержней на плоскость хОу являются касательными к окружности диаметром d с центром в точке О. В процессе работы станка гильза может повора чиваться вокруг своей оси от этого исходного положения ((р. = 0 ) в противоположных направ лениях теоретически вплоть до указанных выше особых положений.

На рис. 3, а, где показан вид станка сверху (с положительного конца оси Oz), предельные углы поворота гильзы вокруг оси Oz обозначены

zl и

ф_гг . При указанном на рисунке значении

Z_max достигается только одно особое положение ( ф_г = ф_й ).

Рассмотрим определение геометрических параметров станка, обеспечивающих его рабочее пространство, ограниченное сферой радиуса R, при движении гильзы без поворота вокруг своей оси, занимающей вертикальное положение.

Для этого необходимо, чтобы при указанном движении гильзы любая ее точка могла быть, совмещена с любой точкой пространства, ограниченного сферой радиуса R с центром, совпадающим с положением этой точки при указанном выше исходном положении гильзы.

При исходном положении гильзы, показанном на рис. 2, длины всех стержней одинаковы и равны Zo. Расчет этой длины проведем для стержня NM.

где b - длина касательной NM'.

Из прямоугольного треугольника OM'N находим

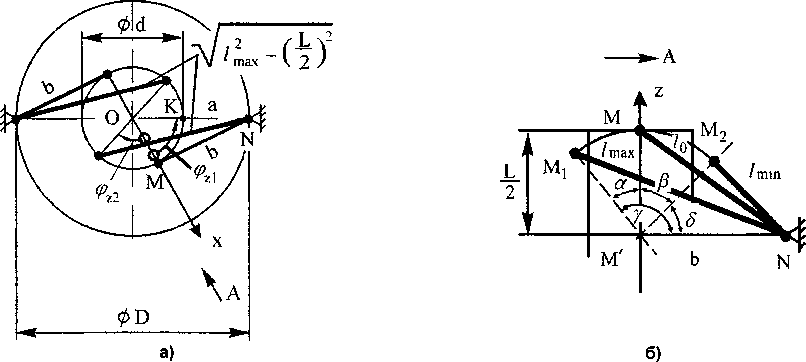
Рис. з

Тогда

Поскольку по условиям задачи точка М, как и любая другая точка гильзы, должна описывать сферу с заданным радиусом R, то при указанном угловом положении гильзы

L4+R;                                         (4)

/'min=^o-R.                                                                       (5)

При других угловых положениях гильзы требуемые длины стержней будут отличаться от рассчитанных по формулам (4) и (5). Наименьшие длины стержней требуются для особого углового положения гильзы ф_г = p_zl. Определим 1_тп для этого положения из треугольника NKK' (см. рис. 2):

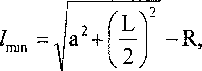
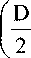
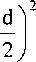
Объединяя равенства (6) и (7), получаем

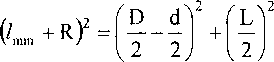
Из выражений (3) и (4) находим

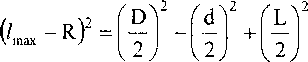
Левые части уравнений (8) и (9) не равны между собой, так как. 1_ШП рассчитывается для особого положения гильзы (^_z = ^_Z1), а Z_max - для исходного (^_z = 0).

В уравнениях (8) и (9) три неизвестных - D, L, Zmax. Поэтому одну из этих величин необходимо задать дополнительно к заданным значениям d и Zmm .

Если — есть не только радиус расположения центров сферических шарниров на фланцах гильзы, но и действительный наружный радиус «тела» гильзы, то должно выполняться неравенство:

(Ю)

2 2

поскольку в противном случае смещение гильзы в горизонтальном направлении на величину R невозможно, так как этому помешают неподвижные шарниры. С учетом того, что действительный наружный диаметр гильзы может быть меньше d, при предварительных расчетах можно принять, что

D = 2R + d.

Тогда из уравнения (8) находим

L = 2V5T^rU.

Из уравнения (9) находим

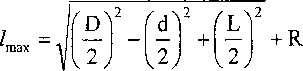
(Н)

Рассчитав по уравнениям (11)—(13) значения D, L и Z_max, можно найти углы а и р отклонения оси гильзы от вертикали при исходном угловом положении гильзы ^_z = 0. При увеличении длин двух противоположных стержней верхней и нижней групп от Z_o до Z_max этот угол будет равен а. При уменьшении длин двух противоположных стержней от Z_o до Z_mm этот угол будет равен Р (рис. 3, б).

Вначале по теореме косинусов найдем угол у:

l2, L

° + n I Z™ax           /2 _/2

у = arccos----—------= arccos———.(14)

bLbL

Формула (14) справедлива при Zmax

Аналогично находим угол S^-.

Ут А2 b I ""'min

= arccos——— bL

5 = arccos----—------ bL

После этого находим углы а и Р".

а = у-90 ; Р = 90° -5.                                                           (16)

Определим угол поворота гильзы вокруг вертикальной оси от исходного до особого положения, т. е. при уменьшении длин всех стержней от Zo до Zmin + 7? (см. рис. 3, а):

d ^i = arccos—.

Предельное значение угла ф_г1 соответствует длине всех стержней, равной Z_max: D² + d² + L²-4Z²

Ф ₂ = arccos-------------— - 90° .                                                (18)

z2              2Dd

I I 1 I . В противном случае ф_гг = 90°, и

, , fD dY fLY это значение достигается при 1-1 = ,— + — + — .

Рассмотрим пример. Задано: R = 120мм; Zmm = 100мм; d = 200мм.

Из уравнения (11) находим D = 2 • 120 + 200 = 440 мм.

Из уравнения (2) находим b2 = 2202 -1002 =38400, b ® 195,959мм .

/ х 2

Далее из уравнения (12) находим I — j =10000 + 24000 = 34000; L — 368,78мм. Из уравнения (1) следует, что 1ц = 38400 + 34000 = 72400; Z_o « 269,07мм , а из уравнений (4) или (13) находим /„„ = 389,07мм. Проверим выполнение неравенства Г = Ь+ —= 380,35     .

Шал        '             * л                           *               Шал        2               2                Шал

Следовательно, угол у достигает 180° при Zmax. Поэтому теоретически а = 90°.

По формулам (15) и (16) рассчитаем углы 3 и Д : 8 = 30,7° ; Д = 59,3°.

Далее находим p_zl = arccos^^ = 62,96°. После этого находим значение Z_z, при котором Фг -Фй. =90°: Z_z = д/(220 +100)² +34 000 » 369,32 max. Из этого следует, что и угол p_z2 =90° теоретически достижим. Итак, при заданных параметрах R = 120mm, Z_mm =100мм, d = 200 мм нашли следующие расчетные геометрические параметры станка: D = 440mm, L = 368,78 мм, Z_max =389,07 мм углы отклонения оси гильзы от вертикали а = 90°; Д = 59,3°, углы поворота гильзы вокруг своей оси p_zl = 62,96°, ф_й = 90° . Следует еще раз отметить, что найденные углы а = 90° и ф_й = 90° скорее всего окажутся нереализуемыми по условиям столкновения конструктивных элементов станка. Реальные значения этих углов могут быть определены при конструировании станка.