Star Coloring Problem: The DNA Solution

Published Online April 2012 in MECS

Through advances in molecular biology [1, 2], it is now possible to produce 1018 or more DNA strands in a tube. Those 1018 or more DNA strands can also be applied for representing 1018 or more bits of information. Biological operations can be used to simultaneously operate 1018 or more bits of information. Or we can say that 1018 or more data processors can be executed in parallel. Hence, it becomes obvious that biological computing can provide a very huge parallelism for dealing with problems in the real world. Especially, the problems from the NP-complete class are well known to be exponentially more difficult than evaluating determinants whose entries are merely numerical. It is very difficult to solve these kinds of problems even if very massive supercomputers are used when the problem size becomes large.

On the other hand, DNA computers have full potential of high performance computing Technology. One test tube can be viewed as a processing unit like standard computer architecture. Furthermore, DNA algorithms using biological operations have natural parallelism because DNA strands are separated melted, annealed) in test tubes in parallel.

Feynman [3] first proposed molecular computation in 1961, but his idea was not implemented by experiment for a few decades. In 1994 Adleman [1] succeeded to solve an instance of the Hamiltonian path problem in a test tube, just by handling DNA strands.

Lipton [4] demonstrated that the Adleman techniques could be used to solve the satisfiability problem. Adleman et al. [5] proposed sticker for enhancing the Adleman- Lipton model. In recent years methods for solving several well known NP- Complete problems [12,13,14,15,16,17,18,19,20] have been proposed.

In this paper, we develop a DNA-based algorithm to solve the star coloring problem, which is a well known NP-complete problem, based on Adleman-Lipton model. we use DNA sequence to construct a solution space for the star coloring problem. Furthermore, this work presents clear evidence of the ability of DNA based computing to solve NPcomplete problems.

The rest of the paper is organized as follows. In section 2, the Adleman-Lipton model is introduced in detail. In section 3, the star coloring problem is defined and the construction of a solution space for the star coloring problem is introduced. In section 4, a DNA algorithm is proposed to solve the star coloring problem of any undirected graph with n vertices for a given three colors. The time complexity of the proposed algorithm is described and the correctness of the algorithm is discussed. In section 5, generalized algorithm is given to solve the star coloring problem of any undirected graph with n vertices for a given l colors, where l is a positive integer.

2.    The Adleman-Lipton Model

DNA is the major information storage molecule in living cells, and billions of years of evolution have tested and refined both this wonderful informational molecule and highly specialized enzymes that can either duplicate the information in DNA molecules or transmit this information to the other DNA molecules.

A DNA (deoxyribonucleic acid) is a polymer, which is strung together from monomers called deoxyribonucleotide. Distinct nucleotides are detected only with their bases. Those bases are respectively, abbreviated as A (adenine), G (guanine), C (cytosine) and T (thymine). Two single strands of DNA can form a double strand, if the respective bases are the Watson-Crick complements of each other - A matches T and C matches G; The length of the single stranded DNA is the number of nucleotides comprising the single strand. The length of the double stranded DNA is counted in the number of base pairs.

The Adleman-Lipton model: The DNA operations in the Adleman-Lipton model [1, 4, 6, 7, and 8] are described below. These operations will be used for figuring out solution of the star coloring problem.

A test tube is a set of molecules of DNA (that is a multi-set of finite strings over the alphabet A, C, G, T). Given a tube, one can perform the following perations:

• 1.    Denaturation: Given a test tube T, Denaturation (T) dissociates each double strand in T into two single strands.

• 2.    Annealing: Given a test tube T, Annealing (T) produces all feasible double strands in T. (The produced double strands are still stored in T after annealing).

• 3.    Synthesis: Synthesis (to produce) a DNA of a desired strand.

• 4.    Amplification: To make copies of the given DNA strands.

• 5.    Cutting: Cut a DNA at a particular place in the strand.

• 6.    Ligation: Ligate DNA strands with complementary sticky ends.

• 7.    Extract: Given a tube T and a short single strand of DNA, S, the operation extract produces two tubes + (T, S) and - (T, S). + (T, S) is all of the molecules of DNA in T which contain the strand S as a sub-strand and -(T, S) is all of the molecules of DNA in T which do not contain the short strand S.

• 8.    Detect: Given a tube T, the answer is ‘yes’ if T includes at least one DNA molecule, and the answer is ‘no’ if it contains none.

• 9.    Discard: Given a tube T, the operation will discard the tube T.

• 10.    Read: Given a tube T, the operation is used to describe a single molecule, which is contained in the tube T. Even if T contains many different molecules each encoding a different set of bases, the operation can give an explicit description of exactly one of them.

• 11.    Copy (T, Ti): In parallel, this operation produces a number of copies, Ti of the set T.

• 12.    Union (T_i, T): This operation in parallel creates the set T which is the set union of the sets T_i.

• 13.    Length-Separate: Given a tube T and an integer n, produce the tube (T, ≤ n) consisting of all strands in T with length less than or equal to n.

3.    The Star Coloring Problem

• 3.1    Construction of solution of DNA sequence for the Star Coloring Problem

Given a graph G = (V, E), where V is the set of vertices and E is the set of edges with |V | = n and |E| = m. A proper coloring of a graph G is called the star coloring if no path of length three in G is bicolored. A proper coloring of a graph G is an assignment of colors such that no two adjacent vertices receive the same color. For a given graph G determining any assignment of 3 colors to G is a star coloring of G or not is an NP-complete problem [9].

In the Adleman-Lipton model, their main idea is to first generate solution space of DNA sequences for those problems resolved. Then, basic biological operations are used to select legal solutions from the solution space. Therefore, the first step of resolving the star coloring problem is to produce a test tube which contains all possible assignment of colors to the vertices of the graph. The input is an undirected graph G = (V, E), where V is the set of vertices and E is the set of edges. |V | represents the number of vertices in V and |E| represents the number of edges in E. Let |V | = n, |E| = m and the three colors be c1, c2, c3.

The initial set which contains an assignment of colors to the vertices of the graph of the form GGGNip1csp1NiCCCGGGNip2csp2NiCCC...GGGNipncspn NiCCC, where s = 1,2,3, pi represents the position of the vertex vi which is a 4-mer DNA sequence, Ni is a 5-mer DNA sequence represents the ith assignment of colors to the given graph where 1 ≤ i ≤ 3n. For different coding of Ni, 1 ≤ i ≤ 3n , the DNA strand GGGNip1csp1NiCCCGGGNip2csp2NiCCC...GGGNipncspn NiCCC represents different assignment of colors to the given graph G. The numbers of vertices are more, use different length of oligonucleotide. An edge from a vertex vi to vj is encoded in two ways as PiCNiCGGGCCCNiCPjC and PjCNiCGGGCCCNiCPiC for all i = 1 to 3n. We encode every edge in two ways to give the effect of the undirected nature of the given graph. The edge vi to vj is viewed as vi to vj and vj to vi. The initial set of DNA molecules encoding all candidate solution to the star coloring problem is synthesized using ABI3948 nucleic acid synthesis and purification system [10, 11].

Illustration:

Consider the following graph.

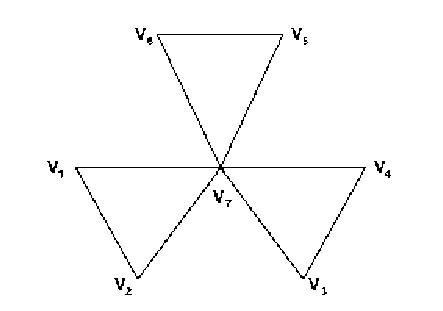
The given graph has 7 vertices. The position of the seven vertices of the graph and colors c1, c2, c3 are encoded as follows:

P 1 : ATGC

P 2 : AATG P 3 : GCTA P 4 : CGAA P 5 : TTCG P 6 : TATC P 7 : GACT c 1 : gtat c 2 : gatt c₃: tatt

Our DNA model involves a long single strand which made of number of sub strands, and each sub strand represents the position of a vertex with an assigned color. The algorithm 1 uses three colors c 1 , c 2 , and c 3 to color the given graph. Single strand in the form GGGN i p 1 c s p 1 N i CCC are used to encode one possible coloring of each vertex in the graph.The sequence N i is used to find the ith assignment of color to the given graph. An assignment of colors to the given graph is of the                                             form

GGGNip1csp1NiCCCGGGNip2csp2NiCCC...GGGNipncspn NiCCC. For different coding of Ni, i = 1 to 3n, this strand represents all possible encoding of the given graph. The middle sequence CCCGGG is recognizable by restriction endonuclease SmaI which can split it at the middle site. For the above given graph, we can generate all possible assignment of colors to the given graph using the DNA codes given above. Thus, all the 37 DNA strands which encode the assignments of colors to the graph can be synthesized using ABI 3948 nucleic acid synthesis and purification system.

4.    The DNA Algorithm for Solving the Star Coloring Problem

The proposed DNA-based algorithm to solve the star coloring problem is described in this section. It can be applied to solve the star coloring problem of any undirected graph with n vertices for a given three colors.

Algorithm.1.

• 1.    Input (T), where the tube T, includes solution space of DNA sequences which are encoding of all possible assignments of three colors to the vertices of the given graph G.

• 2.    For j = 1 to n

• 3.    For s = 1, 2, 3 and all k such that (j, k) ∈ E

• 4.            T 1 ← + (T, p j c s p j )

• 5.            T 2 ← - (T, p j c s p j )

• 6.            T 3 ← + (T 1 , p k c s p k )

• 7.            T 4 ← - (T 1 , p k c s p k )

• 8.           discard (T 3 )

• 9.         T =T 2 ∪ T 4

• 10.    EndFor

• 11.    EndFor

• 12.    If Detect (T) = yes then

• 13.    Copy (T, (T′, T′′))

• 14.    Add multiple copies of DNA strands GGGCCC to the test tube T′, which in turn produces partial double stranded DNAs with restriction site CCCGGG

• 15.    Add the restriction enzyme SmaI to the test tube T′, it cuts the restriction site CCCGGG , giving rise to the GGGCCC

• 16.    Add DNA strands that represent the edges of the graph to the test tube T′.

• 17.    Generate all possible walks of different length in the test tube T′.

• 18.    T′← (T′, = 112)

• 19.    If Detect (T′) = yes then

• 20.    For 1 ≤ j, k, l, m ≤ n, j ≠ k ≠ l ≠ m

• 21.    T′ ← + (T′, v j )

• 22.    T′← + (T′, v k )

• 23.    T′← + (T′, v l )

• 24.    T′← + (T′, v m )

• 25.    EndFor

• 26.    Copy (T′, (U 1 , U 2 , U 3 )

• 27.    U 1 ← - (U 1 , c 1 )

• 28.    U 2 ← - (U 2 , c 2 )

• 29.    U 3 ← - (U 3 , c 3 )

• 30.    Union ((U 1 , U 2 , U 3 ), T′)

• 31.    If Detect (T′) = No then

• 32.    Every proper coloring of the given graph G in T′′ is the star coloring of the given graph G.

• 33.    else

• 34.    The surface is attached with the complement of N i , 1 ≤ i ≤ 3ⁿ, pass the content of the test tube T′ through this surface. The paths of length 3 which are bicolored will attach to the complements of N_i. The sequence N i , which are free from hybridization are separated from the surface and pour into the test

• 35.    If Detect (T′′) = yes

• 36.    Proper colorings in T′′ are star coloring of G.

• 37.    else

• 38.    Star coloring is not possible

• 39.    else

• 40.    Every proper coloring in T′′ is a star coloring

• 41.    else

• 42.    No coloring is proper coloring.

• 4.1    Implementation of the Algorithm

GGGCCC

proper coloring of the vertices of the given graph.

tube T′′ which contains all proper coloring to the given graph G. By PCR, keep all double stranded DNA in the test tube T′′.

This section describes the implementation of the algorithm.

• •    Start with all the DNA sequences that represent the assignments of colors to the given graph G.

• •    Eliminate all the DNA strands that do not represent the proper coloring of the graph. For each edge (j, k) ∈ E, remove the strands from a test tube T, that contain subsequences p j c_sp j , p_kc_sp_k, where s = 1, 2, 3.

• •    If the test tube T does not contain DNA strands, then conclude no coloring is a proper coloring. If not copy the content of the test tubes into two test tubes T′ and T′′.

• •    Add multiple copies of DNA strands GGGCCC to the test tube T′, which in turn Produces partial double stranded DNAs with restriction site

• •    Add the restriction enzyme “SmaI” to the tube T′, it cuts the restriction site, giving rise to the proper coloring of the vertices of the given graph G.

• •    Add multiple copies of all the DNAs encoding the edges of the graph in the test tube T′ along with the ligation enzyme. All possible walks in the given graph are generated.

• •    Form the tube T′, keep only the DNA strands of length 112 and discard the rest. This is done by the step T ′ ← ( T′, =112). Each vertex is encoded by a DNA sequence of the form GGGN i P 1 C s P 1 N i CCC. The position P i of the vertex v i is a 4-mer DNA sequence and N i is a 5-mer DNA sequence and the color of the vertex is encoded by 4-mer DNA sequence. Every vertex in the graph with color is encoded by 28-mer

DNA sequence. A path of length 3 contains 4 vertices. Therefore, every path of length three is encoded by 28*4= 112 – mer DNA sequence. The step T ′ ← ( T′, =112) selects all walks of length 3 for every proper coloring of the graph without any confusion. This is accomplished by gel electrophoresis technique.

• •    If the test tube T′ contains a DNA strand then proceed to step 20. Otherwise every proper coloring in T′′ is a star coloring.

• •    Checking the distinctness of the vertices of the walks obtained in steps 20-25: produce multiple copies of complement of the vertex v 1 and pour into a test tube T′, complement of v 1 anneal to the vertex v 1 . In a test tube T′, we have three different types of DNA strands. The vertex v 1 either occur twice or once or no occurrence in the DNA strands. Remove all DNA strands in which v 1 occurs twice using gradient centrifugation process. Denature all the remaining strands in the test tube T′ to get the single stranded DNA. Repeat this process to all the remaining vertices. After completing this process the test tube T′ contains all paths of length 3.

• •    Copy the content of the test tube T′ into three test tubes U 1 , U 2 , U 3 . The test tube U 1 retains all the DNA strands that do not contain c 1 as a substring, the test tube U 2 retains all the DNA strands that do not contain c 2 as a substring, and the test tube U 3 retains all the DNA strands that do not contain c 3 as a substring. This step can be accomplished by the operation separation.

• •    Pour the content of the test tubes U 1 , U 2 , U 3 into a single test tube T′. If the test tube T′ does not contain a DNA strand every proper coloring of the given graph G is a star coloring of G. Otherwise the surface is attached with the complement of N i , 1 ≤ i ≤ 3ⁿ, pass the content of the test tube T′ through this surface. The paths of length 3 which are bicolored will attach to the complements of N i . The sequences N i , which are free from hybridization are separated from the surface and pour into the test tube T′′ which contains all proper coloring to the given graph G. By PCR, keep all double stranded DNA in the test tube T′′. If Detect (T′′) = yes, then the proper colorings in T′′ are star coloring of G.

• 4.2    The Complexity of the DNA Algorithm

• 4.3    Correctness of the Algorithm

Otherwise star coloring is not possible.

The star coloring problem with three colors for any undirected n-vertex graph G can be solved with O (n2) biological operations in the Adleman-Lipton model.

The algorithm described in section 4 can be applied for solving the star coloring problem for any undirected n-vertex graph G with given three colors. This Algorithm includes three main steps. The steps 2-11 are mainly used to determine the proper coloring of G and to remove illegal coloring of G from all of the 3n possible assignment of colors to the given graph G. The steps 2025 select all paths of length 3. The steps 26-30 are used to check the bicoloredness of the path of length 3. For each vertex vi ∈ V , 1 ≤ i ≤ n and the three colors c1, c2, c3, the steps 4 and 5 take 3n extraction operations. Since every vertex vi ∈ V , has at most n-1 adjacent vertices, the steps 6 and 7 take 3n×3(n-1) extraction operations. The step 8 takes 3n discard operations. The steps 12-19 take one step each to perform cutting the restriction site, adding DNA strands that represent the edges of the graph and to generate all possible walks. The steps 20-25

need 4n biological operations to detect the path of length 3. The steps 26 and 30 take one step each to copy and union of the content of the DNA strands. The steps 27, 28 and 29 take one step each to detect the DNA strands in which only two colors are used. The steps 31 and 35 take one step each to detect the content of the test tube. Hence, the time complexity of Algorithm is O (n2) biological operations in the Adleman-Lipton model.

The star coloring problem with three colors for any n-vertex undirected graph can be resolved using the algorithm proposed in section 4.

The input of the algorithm is a test tube, which contains all 3n possible assignment of colors to the given n- vertex undirected graph G.

First the algorithm detects all possible proper coloring of G by repeating the steps 2 to 11 for n number of times. The first test tube T 1 contains all the DNA strands in which the first vertex v 1 has the color c 1 , the second test tube T 2 contains all the DNA strands in which the first vertex v 1 has the color c 2 or c 3 . The third test tube T₃ contains all the DNA strands in which the vertex v₁ and its adjacent vertices have the color c₁. The fourth test tube T 4 contains all the strands in which the vertices adjacent to the vertex v 1 have the colors c 2 or c 3 . Therefore the test tube T 3 collects all the strands in which the vertices adjacent to v 1 and the vertex v 1 have the same color and the test tube T 4 collects all the strands in which the vertices adjacent to v 1 and the vertex v 1 have different colors. Step 8 uses the “discard operation” to remove all the illegal coloring to the vertex v 1 and its adjacent vertices for the color c 1 . Step 9 merges the content of the tubes T₂ and T₄. Now the test tube T contains the DNA strands in which the first vertex v₁ has the color c₂ or c₃ and the DNA strands in which the first vertex v 1 has the color c 1 and its adjacent vertices have different colors c 2 or c 3 . By repeating the same procedure for the vertex v 1 with the remaining two colors c 2 and c 3 , the test tube T contains all the DNA strands in which the vertex v 1 and its adjacent vertices have different colors. The steps 2-11 are repeated for all the remaining n-1 vertices. If the test tube T does not contain a DNA strand, no coloring is a proper coloring otherwise copy the content of the test tube T into two test tubes T′ and T′′. Add multiple copies of DNA strands GGGCCC to the test tube T′, which in turn produces partial double stranded DNAs with restriction site. Now, the algorithm checks the star coloring for each proper coloring of the given graph G. Add the restriction enzyme “SmaI” to the tube T′, which in turn cuts the restriction site, giving rise to the coloring of the vertices of the graph. Add DNA strands that represent the edges of the graph to the tube T′. By ligation reaction all the walks of different length are generated in the tube T′. In coding, the 3ⁿ assignment of colors to the graph is distinguished by the sequence Ni, the edges are encoded with all the sequences N_i, 1 ≤ i ≤ 3ⁿ , by ligation reaction all walks are generated for different assignment of colors without confusion.

Next the test tube T′ retains all the DNA strands of length 112 (that is a walk of length 3). If the test tube T′ contains no strand then every proper coloring in T′′ is a star coloring. Otherwise, the steps 20-25 are used to find all the paths of length 3. Now the test tube T′ contains all the path of length 3. Copy the content of T′ into three test tubes U1, U2 and U3. The test tube U1 collects all the strands which have the colors c2 and c3. The test tube U2 collects all the strands which have the colors c3 and c1. The test tube U3 collects all the strands which have the colors c1 and c2. The step 30 uses “union operation” to merge the contents of the test tubes U1, U2 and U3 into one test tube T′. If the test tube T′ does not contain a DNA strand every proper coloring of the given graph G is a star coloring of G. Otherwise the surface is attached with the complement of Ni, 1 ≤ i ≤ 3n, pass the content of the test tube T′ through this surface. The paths of length 3 which are bicolored will attach to the complements of Ni. The sequences Ni, which are free from hybridization are separated from the surface and pour into the test tube T′′ which contains all proper coloring to the given graph G. By PCR, keep all double stranded DNA in the test tube T′′. If Detect (T′′) = yes, then the proper colorings in T′′ are star coloring of G. Otherwise star coloring is not possible.

5. The DNA Algorithm for Solving the Star Coloring Problem with l Colors

We can extend Algorithm1 to solve the star coloring problem with l colors. The following DNA algorithm is proposed to solve the star coloring problem of any undirected graph with n vertices for a given l colors, where l is a positive integer.

Algorithm.2.

• 1.    Input (T), where tube T, includes solution space of DNA sequences to encode all lⁿ possible assignment of colors to the vertices of the given graph G.

• 2.    For j = 1 to n

• 3.    For s = 1, 2, 3, ... , l and all k such that (j, k) ∈ E

• 4.         T1 ← + (T, pjcspj)

• 5.         T2 ← - (T, pjcspj)

• 6.         T3 ← + (T1, pkcspk)

• 7.         T4 ← - (T1, pkcspk)

• 8.        discard (T₃)

• 9.      T =T2 ∪ T4

• 10.    EndFor

• 11.    EndFor

• 12.    If Detect (T) = yes then

• 13.    Copy (T,( T′,T′′))

• 14.    Add multiple copies of DNA strands GGGCCC to the test tube T′, which in turn produces partial double stranded DNAs with restriction site CCCGGG

• 15.    Add the restriction enzyme SmaI to the test tube T′, it cuts the restriction site CCCGGG , giving rise to the GGGCCC

• 16.    Add DNA strands that represent the edges of the graph to the test tube T′.

• 17.    Generate all possible walks of different length in the test tube T′.

• 18.    T′← (T′,=112)

• 19.    If Detect (T′) = yes then

• 20.    For 1 ≤ j, k, l, m ≤ n, j ≠ k ≠ l ≠ m

• 21.       T′← + (T′, vj)

• 22.       T′← + (T′, vk)

• 23.       T′← + (T′, vl)

• 24.       T′← + (T′, vm)

• 25.    EndFor

• 26.    For r = 1 to l

• 27.    For s ≠ r, 1 ≤ s ≤ l

• 28.    T′← + (T′, cr)

• 29.    T′← + (T′, cs)

• 30.    For t = 1 to l, t ≠ r, s

• 31.              T′← + (T′, ct)

• 32.    EndFor

• 33.    EndFor

• 34.    EndFor

• 35.    If Detect (T′) = No then

• 36.    every proper coloring of the given graph G in T′′ is the star coloring of the given graph G.

• 37.    else

• 38.    The surface is attached with the complement of N_i, 1 ≤ i ≤ 3ⁿ, pass the content of the test tube T′ through this surface. The paths of length 3 which are bicolored will attach to the complements of Ni .The sequence Ni , which are free from hybridization are separated from the surface and pour into the test tube T′′ which contains all proper coloring to the given graph G. By PCR, keep all double stranded DNA in the test tube T′′.

• 39.    If Detect (T′′) = yes

• 40.    Proper colorings in T′′ are star coloring of G.

• 41.    else

• 42.    Star coloring is not possible

• 43.    else

• 44.    Every proper coloring in T′′ is a star coloring

• 45.    else

• 46.    No coloring is proper coloring.

6.    Conclusion

GGGCCC

proper coloring of the vertices of the given graph.

DNA computing is a computational paradigm that provides advantages over conventional electronic computing techniques. 1 μmol of DNA in 1 liter of water contains about 1018 strands. If we consider every strand as a processor and that operations takes several minutes, 1000s, then such a DNA based computing would execute 1015 operations per second. If the ligation of two DNA molecules is considered as a single operation, the number of operations per second during the ligation step would exceed that of current super computer by more than thousand fold. The major advantage of DNA computing lies in its high parallelism.

In this paper, we present DNA based algorithm for solving star coloring problem based on biological operations in Adleman-Lipton model. Our algorithm can determine not only the star coloring but also all the star coloring of the given graph in polynomial time. The efficiency of our method can be seen from the time complexity of our algorithm O (n2).