Static Security Enhancement and Loss Minimization Using Simulated Annealing

Published Online March 2013 in MECS

Large interconnected power systems have grown in their demands to high degree of security during their normal and abnormal operation. So far, power systems can be considered the most complex control systems in existence. Power systems are highly interconnected, extremely complex and can spread over vast areas or even over continents. Accordingly, power systems design and operation must make sure that all operating variables are adequately controlled and fall within their acceptable ranges during the power system operation. Power system security main goal is to ensure proper system operation within acceptable limits and with suitable security margins. On the other hand, failure of power systems to operate securely can lead to outages which may have wide range of consequences on power systems, users and equipment including; power interruption to customers, damage of equipment, crucial financial losses, or even loss of life. Technical and economic revenues can be maintained by ensuring power system security [1, 2].

With recent trends of the deregulated electricity markets, modern power systems have been forced to operate closer to their security boundaries. This has encouraged the need for fast and accurate assessment of power system security, focusing on the ability of the power system to maintain the electrical energy delivery from the generating units to the end users, especially under unexpected contingencies such as modifications or sudden changes of the operational conditions [3].

Power system security assessment is classified into transient security, dynamic security and static security [4-7], Static security assessment, starts from the grid topology and structure and energy market transactions, performs a load flow solution to verify that electrical constraints (bus voltages values between prescript minimum and maximum) and thermal constraints (power transmitted on branches does not exceed the imposed limit). If these conditions are not respected the system is not secure from the static security point of view. Static security is guaranteed only if the electrical and thermal constraints are verified for all cases.

The same authors in [8] presented a probabilistic neural network (PNN) based classifier to judge the static security of the power system. The proposed classifier classifies the security of the power system based on the voltage profile of each bus in reference to changes in the generation and load profile in the system as well as in case of single and double line outage contingencies. The probabilistic neural network is used and compared with the radial basis function neural network (RBFNN) and the back-propagation neural network (BPNN). The PNN classifier shows superior results in comparison to other techniques. The proposed methodology has been examined using three IEEE standard test systems, where the input to the neural network is the voltage profile at each bus in case of load variation contingency or the network line status topology in case of single and double line outage contingencies, the output of the PNN classifies the security of the power system into three classes, normal, alert and emergency.

In [9], the same authors introduced a classifier based on gene expression programming (GEP) for assessing the static security of IEEE standard test systems under load variation as well as single and double line outage contingencies. The GEP based classifier introduced the best results in terms of classification accuracy and reduced classification error when compared with probabilistic neural network, radial basis function neural network and back-propagation neural network based classifiers.

The static security enhancement problem has gained a lot of interest in the literature. Many algorithms have been proposed to enhance the static security of the power system. Different mitigation techniques have been proposed for alleviating the contingencies and restoring the system to the secure state. Among the method utilized are: generation re-scheduling, load shedding, use of control equipment including fixed and switched shunt capacitors, fixed series capacitors, thyristor controlled series capacitors, static synchronous compensations and so forth. A set of algorithms for security-constrained optimal power flow (SCOPF) and their configuration in an integrated package for realtime security enhancement are presented in [10].

A methodology is presented in [11] for applying pattern recognition techniques and a parallel architecture in the monitoring and enhancement of power system static and dynamic security. The work takes advantage of an advanced data structure which supports the proposed parallel architecture with high evaluation accuracies, computational savings, flexibility of formulation and expansion. This approach has been tested on practical transmission systems. The development and results of an expert system using PROLOG for enhancing system voltage control were presented. Based on this methodology, the operators can be provided with a priority list for searching the best available control measures after each-contingency. Further, the consequence of each chosen control measures can be-predicted beforehand. The algorithm makes use of the knowledge about the system, sensitivity factors, operating rules, operator's experience and other requirements for good system operation.

The TCSC is one of the most effective Flexible AC Transmission System (FACTS) devices. It offers smooth and flexible control of the line impedance with much faster response compared to the traditional control devices. While numerous studies concerning the utilization of these devices, have been carried out so far, most of the research has focused on issues such as transient stability improvement, sub-synchronous resonance (SSR) mitigation, damping of power swings, avoiding voltage collapse, etc. Reference [12] is concerned with the enhancement of steady state system security against single contingencies via the use of TCSC’S. Placing TCSC’S at selected branches requires the analysis of the system behavior under all possible contingencies. A systematic procedure to place and operate TCSC’S in a power system is presented. First the “Single Contingency Sensitivity (SCS)” criterion for a given branch flow is defined. This criterion is then used to develop a branch’s prioritizing index in order to rank branches for possible placement of TCSC’S. Finally, optimal settings for TCSC parameters are determined for important contingencies. An example system is used to illustrate the implementation of the proposed method. The same authors of [12] introduced the same procedure in [13] with enhancement to determine the setting of the thyristor controlled series capacitors and applied it to the IEEE 118-bus test system in addition to the 14-bus test system for the purpose of eliminating or alleviating the line overloads in addition to minimizing the transmission losses of the power system.

A technique to identify critical double line outages and enhance static security by optimal placement of FACTS devices using heuristics-based Genetic Algorithm (GA) is proposed in [14]. Two indices have been used for contingency screening: double line contingency index (DCI), based on line overflows, and voltage sensitivity index (VSI), and based on bus voltage violations. Contingency screening is treated as the primary optimization problem with an objective of finding all double line outages with maximal DCI and VSI. The VSI gives a measure of total magnitude of voltage exceeded at all buses due to a specific contingency and the DCI gives a measure of total overflow in all the branches due to a specific contingency. The selection of critical contingencies has been carried out using genetic algorithms with a local search technique. The GA solves the primary optimization problem of finding all the critical double line outages. Once a critical combination of double-line outage is identified, the GA searches possible combinations of lines having any of these two outages. Two different GA’s have been used with fitness evaluated based on DCI and VSI respectively. The use of shunt capacitors and TCSC’s for security enhancement due to double-line contingencies has been investigated. The technique is demonstrated using IEEE 14 bus and IEEE 30 bus systems with results indicating that voltage violations are easily rectified.

The application of Particle Swarm Optimization (PSO) technique is presented in [15] to find the optimal setting of TCSC’s in order to eliminate or minimize line overloads under single contingency or critical double contingency and to minimize the installation cost of TCSC’s . The proposed approach uses Contingency Sensitivity Index (CSI) to rank the system branches according to their suitability for installing a TCSC. Once the locations are determined, particle swarm optimization technique is used to find the best settings for the installed TCSC’s to eliminate or minimize the line overloads in case of all the possible single contingencies or critical double contingencies and to minimize the installation cost of TCSC’s. The voltage magnitude at each bus and the line flow through each branch for all the buses and branches respectively, have been considered as inequality and equality constraints. The proposed approach enhances the static security of the power system with minimum installation cost of TCSC. The IEEE 6-bus and 30-bus systems are used to validate the proposed approach. The total number of overloads is reduced and in 30 bus system, the severity of overloading is reduced after installing TCSC’s.

In [16], it is illustrated that voltage security is a crucial issue in power systems especially under heavily loaded conditions. Optimal locations of STATCOM have been identified to enhance power system voltage security by using an artificial intelligent technique namely the genetic algorithm. The proposed method demonstrates the improvement of voltage security margin. It is implemented to a modified IEEE 14-bus system. The study is carried out for the aim of voltage security margin enhancement. Simulation results through the modified IEEE 14-bus validates the efficiency of the optimal placement of a STATCOM. Active power losses in practical power systems were reduced via the proposed technique. Cost-benefit analysis showed the significant saving using such FACTS devices. The authors claim that this algorithm may also be effective for the optimal placement of the STATCOM in the large scale power systems.

The goal of the methodology developed of [18] is to alleviate/eliminate overloads on the transmission lines and to maintain the voltages at all load buses within their specified limits through an optimal placement and optimal setting of SVC under different network contingencies. The optimal location of SVC is identified by a new index called Single Contingency Voltage Sensitivity (SCVS) index. The SCVS index is determined only for the important contingencies, which are actually causing problems for system security. The important contingencies are short listed using the Voltage Performance Index (PIV). The SCVS values are calculated for all load buses of the system. The load buses are then ranked according to their SCVS values. In general, the bus with larger value of SCVS is considered as more sensitive and is ranked first. The SVC should be placed according to the ranking made based on SCVS. The SVC should be placed at a bus having most positive SCVS index. Also additional criterions have also been used while deciding the optimal placement of FACTS device i.e., the SVC should not be placed at a bus, where, the injected MVAR already exists. A bus that is selected for the optimal placement of SVC is shunted at a bus along with the other shunted elements, which will provide the most efficient control of the voltage and as well as power flows and will enhance the steady state security of the system. The effectiveness of the method is carried out on 6-bus system. The six-bus system has got eleven transmission lines with a voltage level of 230 kV. Once the location is identified, the optimal setting of SVC is determined to achieve the goal and enhance the power system performance under network contingencies. The optimal location and the optimal setting of SVC are obtained through a programming code written in MATLAB. The results presented authenticate the effectiveness of the methodology demonstrated.

An application of a coordinated SVC is reported in [19] as additional control in reactive power (VAr) optimization problem and analyzes the impact on system loss minimization and voltage improvement. Unlike the general SVC, the coordinated SVC model controls internal, local, and remote devices simultaneously. It has two modes of operation:

Voltage control mode; and Q control mode. The functions of the coordinated SVC are analyzed, and implemented in the practical power systems. A performance index for evaluating the impact of VAr optimization with coordinated SVC model on loss minimization and voltage improvement are also presented.

An Evolutionary Computing (EC) technique for solving constrained reactive power control (CRPC) problem is presented in [20] in the attempt to enhance voltage stability under contingencies, while minimizing transmission loss and maintaining voltage level at an acceptable level. In this study, evolutionary programming (EP) was chosen as the evolutionary computing technique for solving the CRPC; taking into consideration two separate objective functions. Static voltage stability enhancement and minimization of real power loss are implemented separately on a reliability test system. The model for CRPC considering multicontingency; generator outages and line outages is formulated. This technique determines the amount of reactive power to be compensated to the system in enhancing the voltage stability or minimizing real power transmission loss in the system when the system under stress and contingencies. Comparative studies performed with respect to Artificial Immune System (AIS). Maximum load ability study was initially conducted to determine the condition of the load bus in the system. Simulation is carried out on the IEEE 30-bus RTS system. Both EP and AIS performed well in most cases. Nonetheless, EP outperformed AIS for both objectives at the selected test buses. In [21], a constrained active power reschedule using immune system for static security enhancement is presented. The study aims to evaluate the static security when a power transmission system is subjected to multi contingencies. In case of severe contingencies; line outages and generator outages have been presented. The CAPR optimization problem has a major influence on economic operation of power systems. This technique determines the amounts of active power during contingencies need to be rescheduled therefore minimizing the transmission loss while keeping an adequate voltage profile and could result in the lowest production cost. The AIS and EP methods are performed on the IEEE 30-bus RTS reliability test system. A performance comparison with EP is also included to highlight the efficiency of the proposed method. Results indicated that AIS outperformed EP in achieving the tasks. Both AIS and EP performed well in most cases. Comparison of the results for both methods has verified the capability of AIS and EP in providing optimal solution.

In this paper a selective procedure to determine the locations and settings of the thyristor controlled series capacitors is presented. The locations are determined by evaluating contingency sensitivity index (CSI) for a given branch for a number of given contingencies. This criterion is then used to develop branches prioritizing index in order to rank branches possible for placement of the thyristor controlled series capacitors. Finally optimal settings are determined by the optimization technique of simulated annealing, where setting are chosen to minimize the overall system losses of the system.

The next section introduces the simulated annealing (SA) artificial intelligence technique, that shall be used in the optimization process for determine the settings of the TCSC’s. The static security enhancement problem is then formulated where thyristor controlled series capacitors are used to enhance the system static security and relieve the single and double line outage contingencies previously assessed in [9]. The procedure for selecting the sensitive branches to install TCSC’s is explained in detail. After placing each TCSC, an optimization process to determine the size of the located thyristor controlled series capacitor is introduced based on the technique of simulated annealing. The settings of the TCSC’s are decided based on minimizing the system losses. The designed algorithm has been applied to 14 bus, 30 bus and 57 bus IEEE standard test systems and the results are analyzed to show the static security enhancement gained then conclusions are driven.

• II.    Simulated Annealing Technique (SA)

The simulated annealing paradigm is a generalpurpose stochastic optimization technique that has proven to be an effective tool for approximating globally optimal solutions to many types of combinatorial optimization problems. Simulated annealing is based on an analogy with the physical annealing process – a technique in the field of condensed matter physics for obtaining the minimum energy state of a solid. The major drawback of the paradigm is its typically high and sometimes prohibitive computational cost.

The Simulated Annealing (SA) algorithm grew from the observation that solving large-scale combinatorial optimization problems is analogous to the annealing of solids in the field of condensed matter physics. The goal of the physical annealing is to achieve a solid’s lowest energy state. This is accomplished by melting the solid in a heat bath and slowly lowering the temperature in order to allow the particles of the solid to rearrange themselves in a crystalline lattice structure. This structure corresponds to a minimum energy state for the solid (i. e. global minimum).

The initial temperature of the annealing process is the point at which all particles of the solid are randomly arranged within the heat bath. As the cooling proceeds, the solid must reach what is known as thermal equilibrium at each temperature before cooling can continue. If the temperature is lowered before thermal equilibrium is achieved, defects will be frozen into the lattice structure and the resulting crystal will not correspond to a minimum energy state (i. e. frozen in a local minimum).

The thermal equilibrium is achieved during the process of physical annealing when the solid has the probability of being in a state with energy, E, according to the equation

Pr { E = E } =

1    (KE J e ^ B ^

Z(T)

where:

• E: is the energy of the state.

Pr: is the probability of the system being in a state of energy, E.

T: is the temperature.

Z(T): is a normalization factor dependent upon temperature T called the partition function.

and K B is the Boltzmann constant.

The probability distribution represented by (1) is usually referred to as the Boltzmann distribution. As can be seen in (1), only the minimum-energy states have a non-zero probability of occurrence as the temperature T approaches zero.

The Metropolis Monte Carlo simulation can be used to simulate the annealing process at a fixed temperature T. The Metropolis method randomly generates a sequence of states for the solid at a given temperature. A solid’s state is characterized by the positions of its particles. A new or perturbed state is generated by displacing a randomly chosen particle by a small distance. The acceptance or rejection of the perturbed state as the next state in the sequence is determined by the Metropolis acceptance criterion given by:

Pr { X k = jlX k - 1

= i } = e

( -^ a ) I K b T )

where: ^AEj : is the difference in energy between the current state X k-1 =i and the perturbed state X k=j . This rule for acceptance is commonly known as the Metropolis criterion.

Therefore if the perturbed state j has lower energy than the current state, i the Metropolis process is continued from the perturbed state. If the energy of the perturbed state is greater than that of the current state, the probability of continuing the sequence from the perturbed state is given by (2).

After a large number of states has been generated and subjected to the Metropolis acceptance criterion, the temporal distribution of the states will approach the Boltzmann distribution.

Therefore, we can simulate the entire annealing process by means of generalizing the Metropolis simulation for solving combinatorial optimization problems. Solutions to a combinatorial optimization problem are analogous to the states of a solid during the annealing process with the corresponding cost of a solution being analogous to the energy of the solid’s state. Since temperature has no equivalent concept in most combinatorial systems to be optimized, it is modeled as a control parameter for use in the SA algorithm that has the same units as cost function. For this reason, the SA control parameter will be referred to as the SA temperature and will be denoted by the symbol tk. The SA algorithm can now be described as a sequence of Metropolis simulations executed at monotonically decreasing temperature values.

SA is started at a high initial temperature t0 with a randomly generated solution to the combinatorial optimization problem being considered. This corresponds to a high-energy state analogous to the random disbursement of a solid’s particles throughout the heat bath at the beginning of the physical annealing process. The initial SA temperature is generally determined, such that almost all solution transitions will be accepted. A generation mechanism is defined for the problem being solved as a means to create a new candidate solution j from the current solution i. The new solution is chosen uniformly at random from the current solution’s neighbourhood. This corresponds to the small random perturbation for the state transition of the Metropolis simulation. SA then makes use of a slightly modified form of the original Metropolis criterion to determine the acceptance of the perturbed solution. Lower cost solutions are always accepted, and higher cost solutions with probability defined by the following equation:

Pr { X k = j | X k - 1

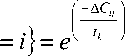
where A C-y is the difference in cost between the current solution i and the perturbed solution j, and t_k is the current SA temperature value associated with the k^th Metropolis trial. The process continues until equilibrium is reached at the current temperature. The temperature is then lowered according to some predefined decrement rule. The system is allowed to regain equilibrium at the new temperature, and the process repeats. This continues until the temperature reaches a low value at which virtually no solution transitions are accepted. At this point the system is considered frozen and the algorithm is terminated.

A chain known as Markov chain that is a sequence of probabilistic trials such that the outcome of any trial is only dependent upon the outcome of the previous trial. Therefore, in SA algorithm, solution transitions correspond to Markov trials and are clearly dependent only upon the previous transition sequence. Therefore, SA can be considered as a number of Markov chains each chain executed at a certain fixed monotonically decreasing temperature.

Basic Element in Simulated Annealing

The design of an algorithm based on simulated annealing consists of four important elements:

• 1.    A set of allowed system configurations

• 2.    A set of feasible moves (perturbation mechanism).

• 3.    A cost function.

• 4.    A cooling schedule.

(configuration space).

• Figure 1 is a flowchart illustrating procedures of the simulated annealing algorithm.

• III.    Problem Formulation

  • 3.1    Optimal Placement of Thyristor Controlled

Series Capacitors

The main goal is to select the best locations and setting of thyristor controlled series capacitors to alleviate the single and double line contingencies previously assessed for static security in [9], to relieve the overloaded lines during contingencies. The optimal location of the TCSC’s shall be determined to be at the most sensitive lines to remove the maximum possible unsecure contingencies. The next step is to perform an optimization process to determine the settings of the TCSC’s and in the same time minimizing the total system losses using the simulated annealing optimization technique.

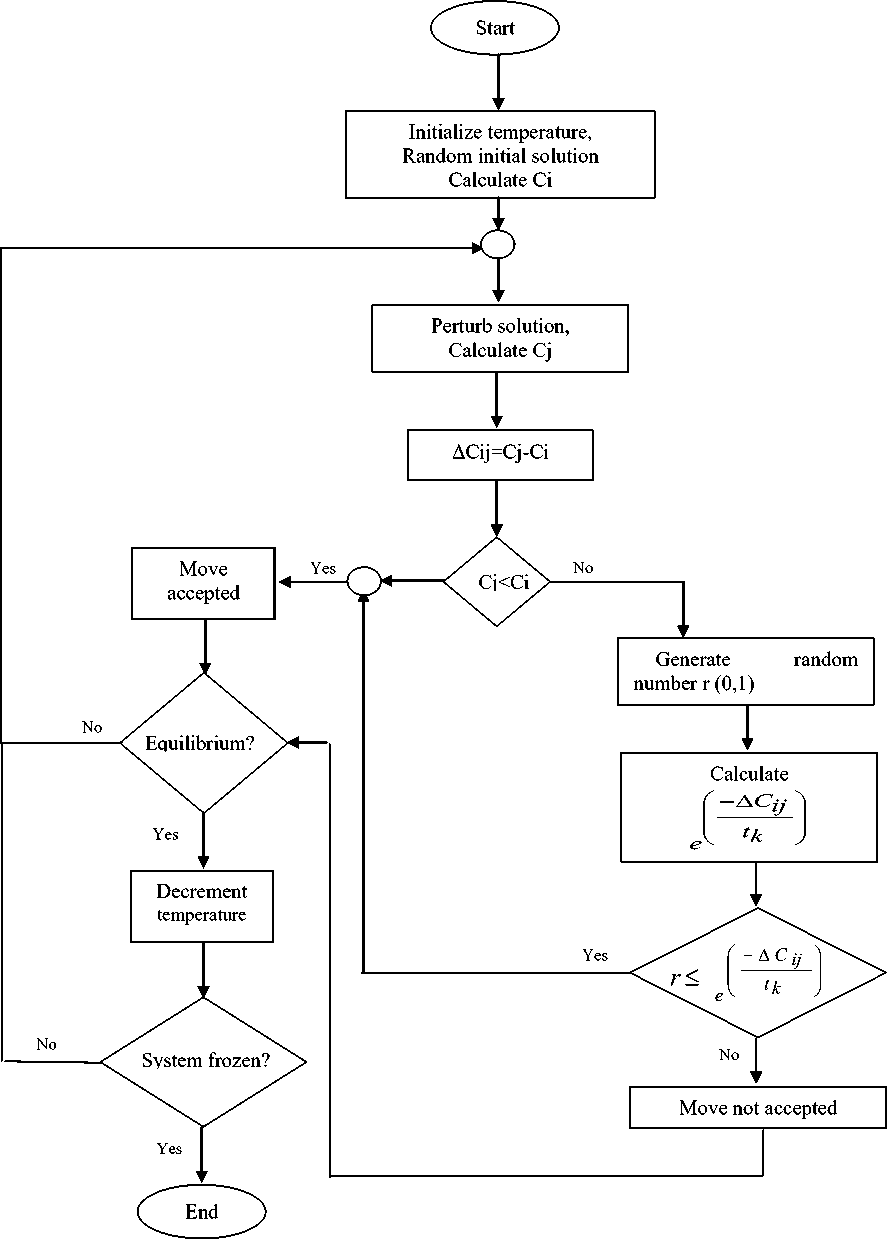
Fig. 1: Simulated Annealing Flowchart

The idea of the proposed approach for TCSC’s placement is a modified algorithm of [12] and [13], in which the algorithm determines a branch which is most sensitive to the largest number of contingencies. A

TCSC that is in series with the chosen branch will provide the most efficient control of the system flows in the largest number of contingencies. The following matrices shall be defined:

Participation Matrix “U”

This matrix is a representation whether or not the corresponding branch is overloaded due to a certain contingency. The participation matrix entries are binary either ‘1’ or ‘0’ depending upon whether or not the corresponding branch is overloaded due to a contingency respectively. This matrix has the following form:

In which p ^{j , cont} and ^{p j , norm} are the power flows through branch j during contingency i at normal or base case respectively.

Contingency Probability Array “P”

This is an array of branches outage probabilities. The probability of branch outage is calculated based on the historical data about the faults occurring along the particular branch in a specified duration of time. It will have the following form:

^Pmx 1 ^{= [} P 1   P 2  ..... P m Г

U

mxn

u11   u12

u 21 u 22

u1n u2n

и , m1

Where ^{p i} is the probability of occurrence of contingency i . Hence the contingency sensitivity index ^CSIj for branch ^j to all the considered contingencies is expressed as the sum of all sensitivities of branch ^j for all contingencies as follows:

where m is the total number of considered

contingencies,

m

CSIj=E pujwj i=1

n is the total number of branches.

If it is assumed that the set of overloaded branches

C during a contingency iis ij , then the elements of U matrix can be expressed as:

Accordingly, the procedure for choosing the optimum locations of TCSCs will be as follows:

uj = 1

'1 j е C i '0 j t C i

Ratio Matrix “W”

This matrix is a representation of the normalized

w excess (overload) branch flows. Its element ij is the normalized excess power flow (with respect to the base case flow) through branch j during contingency i and the matrix is expressed as follows:

w11 w12   ... ..   w1n w21 w22   .. ...   w2n W = . wm2

• •    For a given set of line outage contingencies calculate the participation matrix, ratio matrix and contingency probability array.

• •    Calculate the contingency sensitivity index for each branch.

• •    Rank the branches in a descending order list according to the maximum contingency sensitivity index.

• •    Choose the number of thyristor controlled series capacitors to be installed.

• •    Place the first thyristor controlled series capacitor in the selected branch with the maximum contingency sensitivity index.

• •    Determine the setting of the thyristor controlled series capacitor using the simulated annealing technique such that the setting of the TCSC will minimize the system power losses.

• •    Repeat the above steps for the available number of chosen thyristor controlled series capacitors to be installed.

where

w ij

w

w mn

p j , cont

p

j , norm

3.2 Optimal Settings of Thyristor Controlled Series Capacitors

The next step after locating the thyristor controlled capacitors is to determine their optimal sizes such that the power losses of the system are minimized while achieving all the static security constraints including bus voltage limits, line loading. This is accomplished by

using the artificial intelligence method of simulated annealing for minimizing the system losses.

Simulated annealing is a general-purpose technique for solving combinatorial optimization problems. The algorithm is presented in the following steps:

Repeat {

Perturb

Evaluate cost function

Accept/update

} until stop criterion = true

A vast majority of current algorithms based on simulated annealing are devoted to unconstrained optimization problems. However, many problems of practical interest in power systems including optimal sizing of thyristor controlled series capacitors belong to constrained optimization problems with both equality and inequality constraints. The basic idea of adapting the simulated annealing to constrained optimization problem is to expand the acceptance rule by adding a feasibility check to its probabilistic selection rule as shown in the following steps: at each temperature the simulated annealing algorithm is performed as follows:

Repeat {

Perturb

Check feasibility (accept or discard)

Evaluate cost function Accept/update

} until stop criterion = true

The function of the feasibility check step serves to monitor the equality and inequality constraints. If any of these constraints are violated the move is discarded and the configuration before this move is retained for the next step. Every move requires the step of feasibility checking which itself involves a distribution load flow study.

Basic Elements in Simulated Annealing

The design of an algorithm based on simulated annealing consists of four important elements: a set of allowed system configurations (configuration space), a set of feasible moves (move set), a cost function and a cooling schedule (rule for decreasing the temperature). The design of these four elements for the optimal thyristor controlled series capacitors sizing problem is as follows:

Configuration Space

It is the set of allowed system configurations over which the optimal solution is searched for. It is very important for the implementation of the SA algorithm since it determines the space the algorithm can move in. In the problem under investigation, the problem is merely a sizing problem. Locations of TCSC’s are known ahead from the previous solution methodology. Every configuration space determines the sizes of TCSC’s at known or given branch locations. The configuration space is defined as follows:

X TCSC  ^{[ X} TCSC 1   X T'CSC 2 X TCSCj

X TCSCk ]

X where TCSCj is the TCSC size at branch j and kis the total number of TCSC’s to be installed.

Perturbation Mechanism

The perturbation mechanism is the way the SA algorithm generates a new system configuration from the current system configuration. The perturbation mechanism will be taking into consideration the range of the allowable sizes of the TCSC’s similar to that in [13] and [15] as follows:

- 0.5 X, <  X_Tr< 0 0.5 X, L     TCSC         L

Where ^{X L} is the original line reactance. A random number shall be generated to determine the TCSC size during each perturbation satisfying the constraints of (11).

Cost Function

The cost function to be used in the SA algorithm or the objective function to be minimized is the total losses of the system.

Cooling Schedule

The cooling schedule contains two components; the initial temperature setting and the temperature decrement rule. These two components are determined empirically to give good results. A large number of independent random solutions are generated, with the mean and standard deviation of the cost values recorded. These values serve as approximations for the expected cost over the solution space E” and the standard deviation of the cost over the solution space °™. This setting assures that nearly all transitions during the course of the first Markov chain are accepted. For all implementations of the cooling schedules presented in this chapter the initial temperature is set such that t0 = °”. The next step in the construction of the cooling schedule is the choice of a rule for lowering the temperature or a decrement rule. For all implementations in this chapter fixed decrement rule is applied with the value of the cooling factor α chosen to be 0.98. The algorithm is considered frozen and stopped when four consecutive Markov chains end with the same value of the cost function or the mean value values of the cost function does not change.

• IV.    Simulation Results

The above mentioned algorithm for placement and setting of the TCSC’s has been applied to the IEEE test systems previously assessed for static security in [9]. Load flow simulations were implemented using MATPOWER3.2 package under MATLAB version 7.6. The simulated annealing algorithm was developed using MATLAB version 7.6. The following tables summarize the simulation results for the different test systems.

IEEE 14 –Bus System

The IEEE 14-bus test system shown in Figure 2 is used to illustrate the proposed algorithm and shows the static security enhancement, where as in [13] and [15] it is assumed that all branches at the higher voltage level are considered candidates for TCSC installations. The area enclosed by the dashed frame, including branches 1-2, 1-5, 2-3, 2-4, 2-5, 3-4 and 4-5, is defined as the branch set H . The apparent power limits for these lines are assigned as 2.0, 0.85, 0.85, 0.85, 0.85, 0.85, and 2.0 p.u., respectively. It is assumed that the outage probabilities of all transmission lines are equal to 0.02.

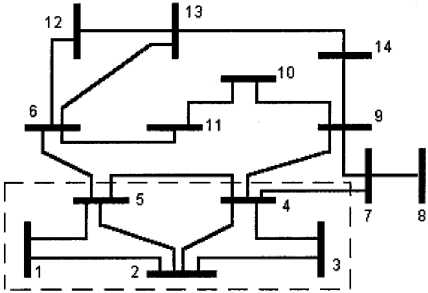
Fig. 2: IEEE 14-Bus Test System

Contingency sensitivity indices are calculated to determine the branches where TCSC shall be installed according the above mentioned algorithm, then the simulated annealing algorithm is used to determine the settings of the TCSC’s in order to minimize the power loss of the system.

Table 1 shows the branches, the contingency sensitivity indices and the ranking where three TCSC’s have been chosen to be installed for enhancing the system static security. Table 2 shows the optimal settings of the TCSC’s installed for the selected locations, where the positive sign indicates increase in the line reactance and the negative sign denotes decrease in the line reactance. Finally, Table 3 presents the enhancement of static security after installing the TCSC’s in comparison with those of [9].

Table 1: Ranks of Branches of IEEE 14-Bus Test System

Number	Branches	CSI	Rank
1	Line 1-2	0.0264	5
2	Line 1-5	0.0232	6
3	Line 2-3	0.0397	4
4	Line 2-4	0.0864	1
5	Line 2-5	0.0597	3
6	Line 3-4	0.0198	7
7	Line 4-5	0.0625	2

Table 2: Optimal Settings of TCSC’S Of IEEE 14-Bus Test System

Number	Branches	Settings (pu)
1	Line 2-4	-0.05967
2	Line 4-5	0.02089
3	Line 2-5	-0.08612

Table 3: Data Generation Results of IEEE 14-Bus Test System

Test Case	Without TCSC installation) [9]	With TCSC installation)
Number of Buses	14	14
Number of Branches	20	20
Operating Scenarios	211	211
Normal State Cases	93	109
Alert State Cases	47	58
Emergency State Case	71	44

It is apparent from the above results that the installation of thyristor controlled series capacitors improved the static security of the test system, where there is an increase of the normal state cases by nearly 17%, increase in the alert cases by 24% and a reduction of the emergency states by approximately 62%. A reduction of the system losses is achieved by the installation of the TCSC’s from 13.393MW in the base case to 13.189 MW after installation of the thyristor controlled series capacitors.

IEEE 30 –Bus System

The proposed static security enhancement algorithm is applied also to the IEEE 30-bus test system. The apparent power limits for the lines are assigned as 2.0 p.u., respectively. The outage probabilities of all transmission lines are equal to 0.02.

Contingency sensitivity index is determined for each branch to determine the branches most suitable for thyristor controlled series capacitors placement, and then the simulated annealing algorithm is used to determine the optimum settings of the TCSC’s for minimizing the power loss.

Table 4 shows each branch along with the contingency sensitivity index and its ranking, where nine TCSC’s have been chosen to be installed for enhancing the system static security similar to [15]. Optimum settings of thyristor controlled series capacitors are shown in Table 5. Finally, Table 6 presents comparison with [9] after installing the TCSC’s and accordingly enhancing the static security of the test system.

Table 4: Ranks of Branches Of IEEE 30-Bus Test System

Branches	CSI	Rank
Line 1-3	0.0635	1
Line 28-27	0.0624	2
Line 9-10	0.0547	3
Line 12-13	0.0425	4
Line 6-10	0.0411	5
Line 24-25	0.0389	6
Line 12-15	0.0247	7
Line 4-12	0.0126	8
Line 21-22	0.0108	9

Table 5: Optimal Settings of TCSC’S Of IEEE 30-Bus Test System

Number	Branches	Settings (pu)
1	Line 1-3	-0.0452
2	Line 28-27	-0.186
3	Line 9-10	-0.05
4	Line 12-13	-0.065
5	Line 6-10	-0.276
6	Line 24-25	0.1208
7	Line 12-15	0.0596
8	Line 4-12	-0.116
9	Line 21-22	0.0104

Table 6: Data Generation Results of IEEE 30-Bus Test System

Test Case	Without TCSC installation) [9]	With TCSC installation)
Number of Buses	30	30
Number of Branches	40	40
Operating Scenarios	821	821
Normal State Cases	256	304
Alert State Cases	67	83
Emergency State Case	498	434

IEEE 57–Bus System

The IEEE 57-bus test system is further used to demonstrate the proposed algorithm with the same settings of apparent power limits for lines and outages probabilities of the IEEE 30-bus system.

Application of the contingency sensitivity index based ranking algorithm together with the simulated annealing optimization technique results in the outcomes shown in Tables 7 to 9.

Table 7 shows the branches ranking as well as the branches contingency sensitivity indices, where nine TCSC’s are installed for enhancing the system static security. Table 8 shows the optimal settings of the TCSC’s. Moreover, Table 9 compares the results with those of [9] after installing the TCSC’s to show the static security enhancement of the test system.

Table 7: Ranks of Branches of IEEE 57-Bus Test System

Branches	CSI	Rank
Line 24-25	0.0854	1
Line 9-12	0.0723	2
Line 11-41	0.0714	3
Line 1-17	0.0709	4
Line 4-5	0.0687	5
Line 26-27	0.0615	6
Line 39-57	0.0582	7
Line 25-30	0.0564	8
Line 18-19	0.0549	9

Table 8: Optimal Settings of TCSC’S Of IEEE 57-Bus Test System

Number	Branches	Settings (pu)
1	Line 24-25	-0.6
2	Line 9-12	0.145
3	Line 11-41	-0.349
4	Line 1-17	-0.043
5	Line 4-5	0.058
6	Line 26-27	0.116
7	Line 39-57	-0.655
8	Line 25-30	-0.1
9	Line 18-19	-0.285

Table 9: Data Generation Results of IEEE 57-Bus Test System

Test Case	without TCSC installation) [9]	With TCSC installation)
Number of Buses	57	57
Number of Branches	80	80
Operating Scenarios	3241	3241
Normal State Cases	1054	1123
Alert State Cases	706	745
Emergency State Case	1481	1373

Table 9 introduces the comparison between the system before and after installation of the thyristor controlled series capacitors, showing an increase in the normal state cases by nearly 7%, increase in the alert cases by 6% and a reduction of the emergency states by approximately 8%. A reduction of system losses is achieved by the installation of the TCSC’s.

• V.    Conclustion

This paper introduced a methodology to enhance the static security of power system using thyristor controlled series capacitors. Thyristor controlled series capacitors offer smooth and flexible control of the line impedance with much faster response compared to the other traditional control devices. The thyristor controlled series capacitors can change the impedance of the line and accordingly enhance the static security of the system during contingencies by relieving line overloads and unacceptable bus voltage profiles. A selective procedure to determine the locations and settings of the thyristor controlled series capacitors is presented. The optimal locations of the thyristor controlled series capacitors are determined by evaluating contingency sensitivity index for a given branch for a given set of contingencies. This criterion is then used to develop branches prioritizing index in order to rank branches possible for placement of the thyristor controlled series capacitors. The locations are determined according to this ranking list in order to alleviate the line overloads and keep the bus voltages within their permissible limits. Optimal settings of the thyristor controlled series capacitors at the selected locations are determined by the optimization technique of simulated annealing, where the settings are chosen to minimize losses of the system. The algorithm has been applied to the IEEE 14-bus, 30-bus and 57-bus test systems with promising results of alleviating the line overloads, enhancing voltage profile, enhancing system static security and minimizing the system losses.