Статическая межотраслевая модель региона в оптимизационной постановке
Автор: Дырхеев Константин Павлович
Статья в выпуске: 4, 2020 года.
Бесплатный доступ
Рассматривается региональная статическая межотраслевая модель с ограничениями по ресурсам и производственным мощностям. Межотраслевая модель представлена в оптимизационной постановке с критерием максимизации суммарного числа комплектов конечного потребления. Выбор оптимального состояния межотраслевой экономики региона осуществляется в пределах краткосрочного периода с фиксированными значениями производственных мощностей и ресурсов. Кроме того, для определенного периода предполагаются неизменными ассортиментные коэффициенты структуры конечного потребления. На основе заданных значений ресурсоемкости выпускаемых продуктов и коэффициентов прямых производственных затрат определяются значения вектора коэффициентов полных затрат ресурсов для линейной модели оптимизации. В результате решения модели определяются максимальное значение комплекта продукции конечного потребления и его положительная двойственная оценка, показывающая возможности роста региональной экономики при ослаблении ограничений на дефицитные ресурсы. Построенная по результатам оптимизационных расчетов региональная таблица «затраты-выпуск» соответствует наилучшему из сбалансированных состояний экономики региона с учетом ресурсных ограничений. Для большего маневрирования дефицитными ресурсами целесообразно включать в оптимизационную межотраслевую модель региона различные способы производства одноименной продукции.
Региональная экономика, межотраслевая модель, оптимизация, ресурсы, производственные мощности, матрица прямых затрат, матрица полных затрат, таблица
Короткий адрес: https://sciup.org/148317646
IDR: 148317646 | УДК: 332.1 | DOI: 10.18101/2304-4446-2020-4-64-70
Текст научной статьи Статическая межотраслевая модель региона в оптимизационной постановке
Проблемам моделирования межотраслевой региональной экономики с учетом ресурсных ограничений уделяется большое внимание в работах отечественных и зарубежных исследователей [3; 6; 7; 8; 12]. Опыт построения и использования соответствующих региональных межотраслевых моделей отражен в научных трудах А. Г. Гранберга, А. О. Баранова, З. Б.-Д. Дондокова, В. Н. Павлова, Г. Р. Серебрякова, М. Н. Узякова, А. А. Широва, А. А. Янтовского и др. [1–5; 9– 11]. Так, А. Г. Гранбергом межотраслевая модель региона интерпретируется как частный случай более развитых оптимизационных моделей [3]. Применительно к определенной территории оптимизационные модели упорядочивают и формализуют выбор наилучших из сбалансированных состояний экономики региона с ограничениями по производственным мощностям и ресурсам с точки зрения определенных критериев оптимальности.
1 Формирование модели
Производственные возможности экономической системы региона определяются технологическими условиями производства, а также объемами и качеством имеющихся ресурсов. Все множество ресурсов разбивается на два подмножества: /1 — продукты и воспроизводимые ресурсы (продукты для конечного и промежуточного использования на определенной территории); ]2 — невоспроизводимые ресурсы, ограниченные в определенном краткосрочном периоде (трудовые ресурсы, производственные мощности предприятий и отраслей, природные ресурсы).
Для экономической системы региона под технологическими условиями производства мы понимаем прежде всего межотраслевые связи и удельные коэффициенты затрат различных ресурсов (продуктов), в том числе воспроизводимых в рамках краткосрочного периода и выражаемых в виде квадратной технологической матрицы Л = (ац^, i,j е К; ( i,j = 1,2, ^,п), где n — количество чистых отраслей (видов экономической деятельности).
В целом межотраслевая модель региона в матричном виде выражается в виде суммы двух квадрантов — промежуточного и конечного потребления.
Естественным стремлением общества является рост конечного потребления в целях повышения народного благосостояния. Однако такой рост в любом перио- де всегда ограничен указанными технологическими и ресурсными возможностями. В этом смысле межотраслевую модель региона целесообразно представлять в оптимизационной постановке в пределах краткосрочного периода.
В составе конечного потребления выделим постоянную и переменную части:
у = w + a v.
Постоянная часть (вектор w = (Wj"), i = 1,2, ..., п) включает минимально необходимые фиксированные объемы продукции для непроизводственного потребления, накопления, возмещения выбытия основного капитала, сальдо выво- за-ввоза продуктов и т. п. Переменная часть включает меняющееся в заданном продуктовом ассортименте конечное потребление, включающее прежде всего потребление отдельных видов домашних хозяйств, а также инвестиции в основной и оборотный капитал. Условными обозначениями переменной части являют- ся: v — суммарное число комплектов конечного потребления в денежном выра жении; а — вектор ассортиментных коэффициентов структуры конечного потребления:
£a j = 1. i=i
а = (« j ), i = 1,2, --,п;
При этом переменная часть конечного потребления максимизируется в рамках краткосрочного периода в заданном ассортименте: v ^ max.
Рассмотрим ограничения статической межотраслевой модели. В краткосрочном периоде наиболее существенными ограничениями роста производства явля- ются наличные производственные мощности, а также общие невоспроизводимые ресурсы (например, трудовые). Введем дополнительные обозначения: х = (x;), у = (у;), (i = 1, .,п) — векторы валовых выпусков и конечного потребления в регионе, Е — единичная матрица размерности п; f = (fj)mxп — матрица ресур-соемкости валовых выпусков, F = (F-y, .„,Fm)' — вектор т видов ресурсов (производственных мощностей), невоспроизводимых в краткосрочном периоде.
Тогда с учетом условия (1), а также ресурсных ограничений запишем в векторно-матричном виде межотраслевую модель в оптимизационной постановке:
х = А x + w +
v ^ max.
Поскольку (Е — А р 1 > 0, а > 0, w > 0, то при v > 0 условие x > 0 всегда выполняется. В результате модельная задача сокращается.
После преобразований имеем: (Е — А)x = w + его, откуда х = (Е —А)- 1w + (Е — А)-W (2)
Подставляя (2) в ограничения по ресурсам (f x < F), получаем f (Е —А)-^v Обозначим P = f (Е — А)- 1<е; R = F — f (Е — А)_ 1w, где: P = (A), ^ = 1, .,m — вектор коэффициентов полных затрат ресурсов для получения одного комплекта продукции конечного потребления; R = (Rг), I = 1, ,„,m — вектор ресурсов, которые могут использоваться для получения переменной части продукции конечного потребления. После преобразований получаем компактную запись модели линейной опти- мизации: Рv < R, v > 0, v ^ max. Обозначив через и = (щ, .,um) — вектор двойственных оценок, запишем двойственную задачу для данной модели: +...+> 1, Ux > 0, ..,um > 0; R^иr+... +Rmum ^ min. Следует отметить, что множество ресурсов принципиально можно разбить на две части: подмножество производственных мощностей (/ = i = 1,2, ...,п) и подмножество других ресурсов (например, трудовых) (I = п + 1, п + 2, ., m): F = (F1, . , ^Vi^n+1, . , Fm)T • Соответственно матрица ресурсоемкости валовых выпусков будет представи- ма в виде двух подматриц: , где f1 = [1;"], л=р1 1,1 L 0^11 L fm 1 Решение модели (4) — (6) с одной переменной очевидно: ∗ =max =min{ }= , МУ ps ( =1,…, ); ∊ , ∊ ․ Для задачи с одной переменной максимальное число комплектов ∗ в кратко- срочном периоде, как правило, определяется при полном использовании произ- водственной мощности какой-то одной агрегированной группы отраслей или при полном использовании только одного вида ресурсов (например, трудовых). Тогда оптимальная двойственная оценка по данной производственной мощности или данному ресурсу будет положительной ( = >0, ∊ ), в то время как по Ps другим ресурсам (производственным мощностям) двойственные оценки будут нулевыми. После нахождения экстремального значения числа комплектов конечной продукции определяем остальные показатели региональной межотраслевой модели, в том числе вектор валовых добавленных стоимостей ( ∗), каждый элемент которого определяется следующим образом: =(1-∑ ) , ( =1,…, )․ После расчета всех показателей формируем региональную таблицу «затраты- выпуск» в стоимостном выражении. 2 Численное моделирование Практические расчеты по региональной межотраслевой модели в оптимизационной постановке были проведены на основе реальных показателей таблицы «затраты-выпуск» по Республике Бурятия за 2013 г. Данные по 14 видам экономической деятельности по специальной методике были оценочно агрегированы до трех укрупненных отраслей (секторов) экономики Республики Бурятия: ( , = 1,2,3; =3): 1) добывающие отрасли, 2) перерабатывающие отрасли, 3) прочие отрасли (в основном сфера услуг). Исходная информационная база по трем секторам экономики республики включает оценочные значения технологической матрицы коэффициентов прямых затрат и матрицы ресурсоемкости, структуры потребления домашних хозяйств, ограничения по производственным мощностям и трудовым ресурсам. Расчетные значения матрицы коэффициентов прямых затрат по трем секторам экономики республики (руб/руб.): 0,145 0,211 0,030 ( × ) = (0,246 0,289 0,287). 0,022 0,041 0,164 Постоянная часть конечного потребления (в млн руб.): = 1145 ․ Вектор ассортиментных коэффициентов структуры конечного потребления: 0,14 =( ) =(0,39); + + =1). 0,47 Матрица ресурсоемкости валовых выпусков ( - единичная подматрица ко эффициентов выхода валовых выпусков продуктов и услуг с соответствующих производственных мощностей по трем секторам; /2— подматрица-строка трудоемкости продуктов и услуг, чел./млн. руб.): =[ ], где: = [0 1 0] , /2 = (0,87; 1,12; 1,34) Вектор ресурсов (производственных мощностей по трем секторам, в млн. руб.; трудовых ресурсов, чел.): F = (81414; 151210; 120174; 413100)7. 3 Результаты расчетов Матрица полных производственных затрат получилась равной: 1,287 0,392 0,181 (Е-А/! = (0,468 1,578 0,558). 0,057 0,088 1,228 Вектора Р и R для ресурсных ограничений (4) оказались следующими: р = /(Е-А/1а = (0,418; 0,943; 0,619; 2,250), ( - ) = (9593; 9656; 11709; 34851), R = F-/(E-A/4w = (71821; 141554; 108465; 378249). По модели линейной оптимизации (4) — (6) находим максимальное значение числа комплектов конечной продукции (в млн руб.): * . (RA R? 141554 v =maxv = m ш{—} = —=----= 150064. , Таким образом, дефицитной является производственная мощность второго сектора экономики республики ( = 151210 млн руб․). Оптимальная двойственная оценка по данной производственной мощности положительна: = =1,06>0. Следовательно, при увеличении производственной мощности вто-Р2 рого сектора число комплектов п* возрастет на 6%, или на величину А п = 1,06 . По другим производственным ресурсам наблюдается их излишек по сравнению с потребностями экономики республики в данных ресурсах. Так, по первому сектору излишек составил 9054 млн руб., или 11,1% от уровня производственной мощности первого сектора, по третьему сектору излишек составил 15 504 млн руб., или 12,9% от уровня производственной мощности третьего сектора. Излишек по использованию трудовых ресурсов составил 24559 чел., или 7,0% от общего количества этих ресурсов. Дальнейшие расчеты выявили следующие значения показателей: ап * = (21009; 58525; 70530)т, у * = w + a п* = (26822; 59670; 79712/, ∗=( - ) ∗ = (72359; 151210; pv * = (62767; 141554 92960/, ∗=( - ) ∗+ ∗ =(72359; 104670/, (∗× ) =( 17800 43700 30040), 151210; 104670; 372565 ) , Ах*3хц = ( 91540 ). На основе полученных оптимальных значений показателей была сформирована таблица «затраты-выпуск» в стоимостном выражении на основе оценочных данных по Республике Бурятия (табл. 1). Таблица 1 Региональная таблица «затраты-выпуск» по Республике Бурятия (оценочные показатели в млн руб.) 1 2 3 Итого У∗ X∗ 1 10 492 31 905 3 140 45 537 26 822 72 359 2 17 800 43 700 30 040 91 540 59 670 151 210 3 1 592 6 200 17 166 24 958 79 712 104 670 Итого 29 884 81 805 50 346 162 035 166 204 328 239 z∗ 42 475 69 405 54 324 166 204 X∗ 72 359 151 210 104 670 328 239 Заключение Таким образом, построенная на региональном уровне таблица «затраты-выпуск» (региональный межотраслевой баланс) соответствует наилучшему из сбалансированных состояний экономики региона с учетом ограничений по производственным мощностям и трудовым ресурсам с точки зрения заданного критерия оптимальности. При этом выявлено, что по данной модели оптимальное состояние региональной межотраслевой экономики достигается при полном использовании только одного ресурса или уровня производственной мощности одного из секторов экономики (в данном случае второго сектора экономики — сектора обрабатывающих производств). Для повышения возможности маневрирования ресурсами, имеющими различную дефицитность, целесообразно в дальнейших исследованиях обеспечивать включение в оптимизационную межотраслевую модель региона различных способов производства одноименной продукции.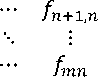
Список литературы Статическая межотраслевая модель региона в оптимизационной постановке
- Анализ и прогнозирование развития экономики Республики Бурятия / под ред. А. О. Баранова, З. Б.-Д. Дондокова. Улан-Удэ: Изд-во БНЦ СО РАН, 2019. 204 с.
- Баранов А. О., Дондоков З. Б.-Д., Дырхеев К. П. Павлов В. Н., Суслов В. И. Методические проблемы формирования информационной базы динамической межотраслевой модели экономики Республики Бурятия // Регион: экономика и социология. 2016. № 4(92). С. 47–68.
- Гранберг А. Г. Основы региональной экономики: учебник для вузов. М.: ВШЭ, 2000. 495 с.
- Дондоков З. Б.-Д. Мультпликационные эффекты в экономике. Улан-Удэ: Изд-во ВСГУТУ, 2000. 143 с.
- Дондоков З. Б.-Д., Дырхеев К. П. Методика проведения аналитических и прогнозных расчетов социально-экономического развития региона на основе межотраслевой модели // Вестник Бурятского государственного университета, 2014. № 2. С. 37–39.
- Колемаев В. А. Экономико-математическое моделирование. Моделирование макроэкономических процессов и систем. М.:ЮНИТИ-ДАНА, 2005. 295 с.
- Леонтьев В. Межотраслевая экономика. М.: Экономика, 1997. 477 с.
- Моделирование и управление процессами регионального развития / под ред. С. Н. Васильева. М.: Физматлит, 2001. 432 с.
- Павлов В. Н. Межотраслевые системы. Математические модели и методы. Новосибирск: Наука, Сиб-е отд-ние, 1986. 219 с.
- 10. Серебряков Г. Р., Узяков М. Н., Янтовский А. А. Межотраслевая модель экономики Ивановской области // Проблемы прогнозирования. 2005. № 2. С. 64–74.
- Широв А. А., Янтовский А. А. Оценка мультипликативных эффектов в экономике: возможности и ограничения // ЭКО. 2011. № 2. С. 40–58.
- Ronald E. Miller and Peter D. Blair. Input-Output Analyses. Foundation and Extensions. Second Edition. Cambridge University Press. The Edinburg Building, Cambridge CB2 8RU, UK, 2009. 289 р.


