Статически-детерминированный метод прогнозирования динамических характеристик параллельных программ

Одним из ключевых фактором, определяющим рост производительности вычислительных систем, является параллелизм обработки данных, поддерживаемый на всех уровнях организации вычислений. Именно благодаря параллелизму стало возможным преодоление барьеров, определяемых технологическими факторами. Современные суперкомпьютеры, производительность которых неуклонно приближается к экзафлопсам, включают в свой состав до миллиона ядер, обеспечивая тем самым высокую степень параллелизма.

Учитывая сложность суперкомпьютерных архитектур, трудно прогнозировать, насколько быстро приложение, предназначенное для современных суперкомпьютеров пе-тафлопсной производительности, будет выполняться на суперкомпьютерах экзафлопсной производительности, каким будет потребление электроэнергии при этом и какие значения

^∗ Статья рекомендована к публикации программным комитетом Международной конференции «Суперкомпьютерные дни в России – 2020».

будут принимать другие параметры, характеризующие производительность параллельного приложения. Количественные характеристики, описывающие выполнение параллельных приложений, такие как, время выполнения, количество операций с плавающей точкой, потребляемая электроэнергия, объем использованной оперативной памяти и другие, будем называть динамическими характеристиками .

Точная экстраполяция характеристик параллельных программ, основанная на интуитивных представлениях и догадках, практически невозможна. Прогнозирование динамических характеристик параллельных программ является актуальной задачей. Прогнозирование необходимо для решения многих задач: разработки и оптимизации алгоритма для определенной архитектуры, оптимизации планирования задач, оптимизации размещения компонентов приложения на гетерогенной архитектуре, выборе архитектуры, наилучшим образом подходящей для конкретного приложения и многих других.

Целью работы является разработка подхода к прогнозированию динамических характеристик параллельных программ, не требующего запуска программы на целевой вычислительной системе, простого в использовании и не требующего много времени для получения прогнозируемых характеристик. В первом разделе статьи приводится классификация подходов к прогнозированию динамических характеристик параллельных программ. Во втором разделе описывается предлагаемый подход к анализу динамических характеристик параллельных программы и проводится его верификация. В заключения представлено краткое описание результатов, полученных в ходе работы, а также указаны дальнейшие направления исследования.

• 1.    Подходы к прогнозированию динамическиххарактеристик

Задачу предсказания значения динамической характеристики h параллельной программы p при входных параметрах v Е V на вычислительной системе с можно представить как вычисление функции h = H(m, v), где m — это модель, которая может быть представлена явно, как объединение двух моделей: модели программы m p и модель вычислительной системы m c .

Можно выделить три подхода к прогнозированию динамических характеристик (рис. 1): аналитический, симуляционный и гибридный. В аналитических подходах предсказание представляет собой вычисление аналитического выражения. В симуляционных подходах предсказание получается посредством симулирования программы или ее редуцированного представления. Гибридные подходы используют как аналитические выражения, так и симуляцию для предсказания значения динамических характеристик.

1.1.    Аналитические подходы

Основанием для построения модели прогнозирования могут являться как исходные тексты параллельных программ, так и информация о поведении программы, собранная во время ее выполнения. В зависимости от этого можно выделить три класса подходов к построению модели: статически-детерминированные (модель строится исходя только из исходного кода программы), эмпирически-детерминированные (модель определяется исходя из данных о результате выполнения программы на наборе параметров) и смешанные (используют как исходный код программы, так и данные о ее выполнении).

В зависимости от степени автоматизации получения модели m аналитические подходы можно разделить на ручные, автоматизированные и автоматические.

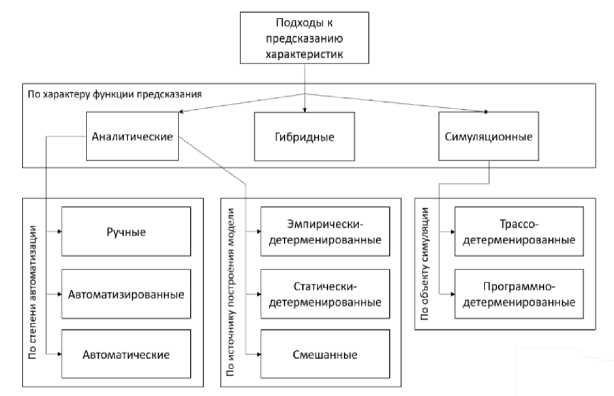
Рис. 1. Классификация подходов к предсказанию характеристик параллельных программ

Ручной подход предполагает, что исследователь создает модель вручную, исходя из своего понимания программы. Можно выделить наиболее общие шаги создания модели, характерные для этого подхода: выделение входных параметров, влияющих на значение исследуемой характеристики, выделение ядер, определение коммуникационного шаблона и возможности перекрытия выполнения передачи данных с вычислениями. У ручного подхода есть два основных недостатка: необходимость глубокого понимания работы программы исследователем и большая трудоемкость.

Автоматизированные подходы более строго формализованы, что позволяет автоматизировать построение модели. С другой стороны, эти подходы зачастую требуют наличия исходного кода программы. В качестве примера автоматизированных подходов можно привести Modeling assertion framework (MA framework) [1] и Performance and architecture lab modeling tool (Palm) [2].

Автоматические подходы требуют минимального вмешательства со стороны исследователя, позволяя существенно облегчить разработку модели. Исследуемая программа в этом случае рассматривается как черный ящик. Автоматические подходы, в свою очередь, можно разделить на две группы: эмпирически-детерминированные и статически-детерми-нированные подходы. В эмпирически-детерминированных подходах модель строится исходя из данных, полученных при запуске параллельной программы. Статически-детерми-нированные подходы предполагают построение модель исходя из статического анализа исходного кода программы.

Эмпирически-детерминированные подходы хорошо изучены, что объясняется простотой их реализации. Наиболее часто встречающийся алгоритм построения модели в рамках данного подхода сводится к двум шагам: сбор значений исследуемой характеристики программы на подмножестве всевозможных значений входных параметров и обучение модели с помощью методов машинного обучения. В статье [3] проводится сравнение двенадцати различных алгоритмов машинного обучения на тестовом наборе мини-приложений Mantevo [4]. Исходя из результатов сравнения авторы делают вывод, что в случае плохо подобранных признаков сложные методы машинного обучения, например, глубокие нейронные сети требуют больший размер обучающей выборки и больше времени на обучение, но при этом имеют большую точность, чем такие простые методы, как МНК (метод наименьших квадратов).

Статически-детерминированные подходы сложны в своей реализации, но в отличие от эмпирически-детерминированных подходов они не требуют запуска целевой программы и зачастую не требуют наличия целевой вычислительной системы, что позволяет использовать их как инструмент суперкомпьютерного кодизайна. Для оценки сложных динамических характеристик рассматриваемые системы используют довольно простые модели, например, Roofline model [5]. В качестве немногочисленных представителей данной группы подходов можно назвать системы COMPASS [6] и ExaSAT [7]. COMPASS генерирует модель программы, используя расширение предметно-ориентированного языка для моделирования производительности Aspen [8], а ExaSAT использует специально разработанное представление модели в формате XML. Отметим, что свободный доступ к обеим упомянутым системам не предоставляется.

1.2.    Симуляционные подходы

В зависимости от источника информации о симулируемых действиях данную группу подходов можно разделить на программно-детерминированные подходы и трассо-детер-минированные подходы. Программно-детерминированные подходы симулируют программу или ее редуцированное представление, а трассо-детерминированные подходы симулируют трассу событий. Трассо-детерминированные подходы зачастую работают быстрее. Они проще в реализации, чем подходы, симулирующие исполнение кода программы, но требуют получения исходной трассы путем исполнения программы или симуляции ее исполнения. Заметим, что трассы могут занимать много памяти. Существует множество симуляторов, предназначенных для работы с последовательными программами. Однако, такие симуляторы непригодны для анализа параллельных приложений.

Примером симулятора, предназначенного для работы с приложениями для больших вычислительных систем, является симулятор BigSim [9]. Получение прогнозируемых характеристик с использованием BigSim можно описать следующим образом. Анализируемое параллельное приложение сначала эмулируется на малом количестве узлов. При этом обеспечивается сбор трассы приложения. Затем проводится симуляция полученной трассы. BigSim поддерживает до 100000 виртуальных MPI-процессов, распределенных по 2000 узлам.

Возможность рассматривать целевую программу в качестве черного ящика и отсутствие необходимости в наличие целевой машины являются главными преимуществами симуляционного подхода. Основным недостатком данной группы подходов является их времязатратность.

1.3.    Гибридные подходы

Гибридные подходы пытаются уменьшить времязатратность симуляционных подходов и увеличить точность аналитических подходов, комбинируя элементы обоих подходов.

В качестве примера инструмента, реализующего гибридный подход, можно привести программный пакет PSINS [10], нацеленный на предсказание времени работы параллельных MPI-приложений. Модель приложения в рамках данного инструмента создается для каждого набора входных параметров. Модель включает в себя информацию о количестве обращений в память и их характере, количестве операций с плавающей точкой и трассы вызовов MPI-функций. Модель целевой вычислительной системы включает информацию о производительности (flop/s), пропускной способности памяти и характеристиках коммуникационной сети. Для получения времени работы приложения сначала определяется время выполнения последовательных участков трасс на целевой вычислительной системе. После этого трассы модифицируются в соответствии с полученными временами и симулируются.

2.    Предлагаемый статически-детерминированный подходк прогнозированию динамических характеристик 2.1.    Описание подхода

Разработка подхода для прогнозирования характеристик проводилась исходя из следующих требований: подход не должен требовать запуска программы на целевой машине, подход не должен быть трудоемок для пользователя, предсказание характеристик не должно требовать много времени.

Исходя из представленных требований, предложенный подход можно классифицировать как статически-детерминированный. Существующие реализации статически-детер-минированных подходов (COMPASS, ExaSAT) не имеют свободного доступа, что мотивировало разработку предлагаемого подхода.

Построение модели происходит на основе статического анализа исходного кода программы (рис. 2). Модель ВС и параметры запуска задаются пользователем, а затем подаются на вход инструментов предсказания динамических характеристик.

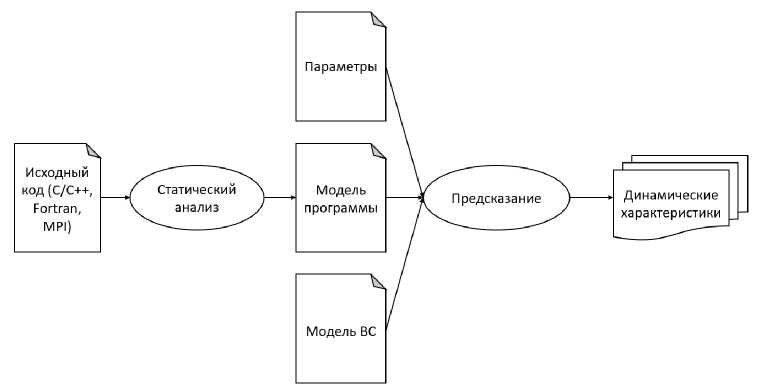
Рис. 2. Схема предлагаемого подхода

Модель программы описывается следующим образом:

m . =< f₁,f₂,^,f_n>,                           (1)

где f i — это модель i -ой функции программы. Функции упорядочены в соответствии с последовательностью их объявления в коде.

где flopsi = — кортеж из функций, возвращающих общее количество операций с плавающей точкой, количество операций с числами одинарной точности и количество операций с числами двойной точности выполняемых функцией, loadBytesi — количество считанных из памяти байт, storeBytesi — количество записанных в память байт, mpiCallsi = — кортеж, содержащий информацию о количестве вызовов MPI-функций, sentBytesi — количество отправленных по сети байт данных, recvBytesi — количество принятых по сети байт данных, loadAccessi — количество запросов на чтение из памяти, storeAccessi — количество запросов на запись в память, mathCallsi = — кортеж, содержащий информацию о количестве вызовов математических функций.

На практике представленная модель программы генерируется статическим анализатором исходя из исходного кода программы. Модель представляется совокупностью python-классов, каждый из которых является моделью функции. Пример python-класса, представляющего фрагмент модели функции, приведен на рис. 3.

class calculate:

@staticmethod def flops(gv_NT? gv_lNX? gv_lNY? gv_lNZ, **kwargs):

@staticmethod def flops4(**kwargs):

return 0

@staticmethod def flops8(gv_NT, gv_lNX, gv_lNY, gv_lNZ, ♦’"kwargs):

return 12 + (-2 + max(2, gv_NT)) * updateValues.flops8(gv_lNX, gv_lNY, gv_lNZ)

@staticmethod def load_access(gv_NT, gv_lNX, gv_lNY, gv_lNZ, **kwargs):

return 28 + (-2 + max(2, gv_NT)) * (updateValues.load_access(gv_lNX, gv_lNY, gv_lNZ) + exchangeShadow.load_access(gv_lNX, gv_lNY, gv_lNZ) + 4)

@staticmethod def store_access(gv_NT, gv_lNX, gv_lNY, gv_lNZ, *‘kwargs):

return 24 + (-2 + max(2, gv_NT)) * (updateValues.store_access(gv_lNX, gv_lNY, gv_lNZ) + exchangeShadow.store_access(gv_lNX, gv_lNY, gv_lNZ) + 2)

Рис. 3. Пример фрагмента модели функции

Модель ВС описывается следующим образом:

m_c =< netLatency,netBandwidth,n₁, .^,n_k >,                 (3)

где netLatency — латентность сети, netBandwidth — пропускная способность сети, n1 , …, nk — модели узлов вычислительной системы.

n₇ =< coreCount, performance, memBandwidth,mathFlops >,         (4)

где coreCount — кол-во ядер на узле, performance — производительность узла (в Gflop/s), memBandwidth = — пропускные способности различных уровней памяти, mathFlops — кортеж с оценками количества операций с плавающей точкой, выполняемых математическими функциями.

Модель ВС также реализуется как python класс. Пример модели вычислительной системы, состоящей из пяти 20-ядерных узлов, приведен на рис. 4.

Прогнозирование времени работы MPI-приложения, исходя из модели программы и модели вычислительной системы, проводится следующим образом:

где Ti — время работы i -го MPI-процесса.

T i

^Tcomm , ^{+ T}comp , ,

где T_comp_t — время, затрачиваемое на вычисления, T_comm. — время, затрачиваемое на межсетевые коммуникации.

^Tcomp,  max

flops,    mem, perfi , bandwidth,

b,

class Polus:	class PolusNode:
@staticmethod	©staticmethod
def IsMultiNodeO:	def isMultiNodeO:	@staticmethod
return True	return False
		def flopsPerCos8():
@staticmethod	©staticmethod def coreCountO:	return 39
def nodeCount():	return 29	@staticmethod
return 4		def flopsPerTanBO :
	©staticmethod	return 39
gstaticmethod	def UBandwidthO:
def getNodetindex):	return 13006	@staticmethod
return PolusNode Sstaticmethod	©staticmethod def dramBandwidtht):	def flopsPerSqrteO: return 1
	return 9900	@staticmethod def flopsPerLog8(): return 39
def networklatencyO: return 66	©staticmethod def performanceO:
@staticmethod	return 5.3	@staticmethod
def networkBandwidtH): return 10OOG	©staticmethod def flopsPerSin8():	def flopsPerlogl0_8() return 39
	return 39

Рис. 4. Пример модели вычислительной системы где flopsi — количество операций с плавающей точкой, выполненных i-ым MPI процессом, perfi — производительность ядра, на котором выполняется i-ый MPI процесс, memi — объем записанных и прочитанных данных, bandwidthi — пропускная способность памяти. Подставляя пропускные способности различных уровней памяти, получаем времена работы при условии, что все запросы в память попадают в этот уровень памяти.

Trnmm- = CdllCoUTlt; * TTetLateiTC^ +-- ^Z'deZ-- , ^commi               ⁷              ^ netBandwidth ’

где callCount i — количество вызовов MPI функций, netLatency — латентность сети, netSize i — размер передаваемых и получаемых данных, netBandwidth — пропускная способность сети. Отметим, что такой способ оценки времени коммуникационного взаимодействия не очень точен. Однако, он требует минимум информации о вычислительной системе. В отличие от симуляции он является простым и быстрым в применении.

2.2.    Верификация подхода

Верификация предложенного подхода проводилась на вычислительном кластере Polus [11]. Исследовались динамические характеристики программы, моделирующей распространение волны в трехмерном пространстве. Вычислительный кластер Polus состоит из пяти узлов, один из которых является головным. На каждом узле установлено два процессора IBM Power8 с графическими процессорами NVIDIA Tesla P100. Для получения пропускных способностей уровней памяти и производительности ядер использовался Empirical Roofline Tool [12]. Для определения латентности и пропускной способности сети использовался тестовый пакет OSU Micro-Benchmarks [13].

Программа, моделирующая распространение волны в трехмерном пространстве, основана на методе конечных разностей с использованием регулярной трехмерной сетки. Сетка разбивается на трехмерные блоки и равномерно распределяется по MPI-процессам. В каждой точке сетки итерационно рассчитываются значения искомых функций согласно заданному семиточечному разностному оператору. Для расчета значения переменной в каждой точке сетки требуется значения шести переменных в соседних точках сетки. На каждой итерации по времени процессы рассчитывают свою часть сетки и обмениваются боковыми гранями с шестью соседними процессами.

Запуски программы проводились на кубических сетках с размерами: 8x8x8, 16x16x16, 32x32x32, 64x64x64, 128x128x128, 256x256x256, 512x512x512. Для сбора информации о количестве операций с плавающей точкой отслеживалось аппаратное событие PM_FLOP.

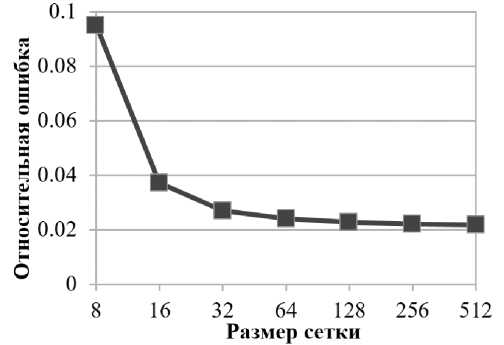
На рис. 5 представлена относительная ошибка предсказания количества операций с плавающей точкой, рассчитываемая как Е_ге х = |(Я- h) ^/ h\ , где h — реальное значение характеристики, Я — предсказанное значение характеристики. Из рисунка видно, что максимальное значение относительной ошибки достигается при минимальных размерах сетки и значение ошибки существенно уменьшается с увеличением размера сетки. Этот эффект объясняется тем, что доля математических функций (sin, cos), используемых для инициализации сетки, больше на маленьких сетках. Количество же операций с плавающей точкой, выполняемых этими функциями, зависит от вычисляемого значения, из-за чего погрешность предсказания для таких функций больше.

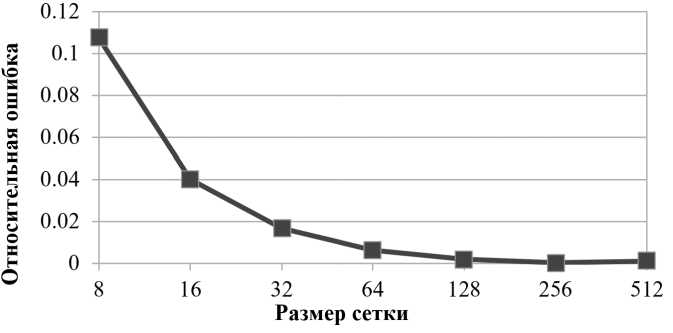
Рис. 5. Относительная ошибка предсказания количества операций с плавающей точкой

На рис. 6 представлены графики относительной ошибки предсказания количества операций доступа к памяти на чтение и запись. Для измерения количества запросов на чтение и запись использовались аппаратные события PM_LD_CMPL и PM_ST_CMPL соответственно. Погрешность при маленьких размерах сетки объясняется большей долей математических функций, а также обращениями к памяти, совершаемыми в процессе динамической линковки, количество которых не зависит от размера сетки.

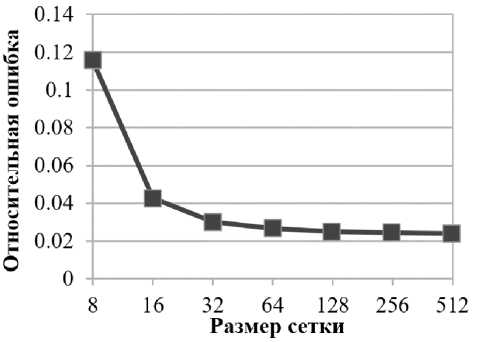
а) Относительная ошибка предсказания

б) Относительная ошибка предсказания количества запросов на запись

Рис. 6. Относительная ошибка предсказания количества запросов на чтение и запись

количества запросов на чтение

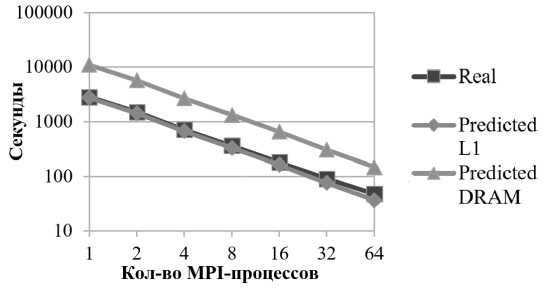
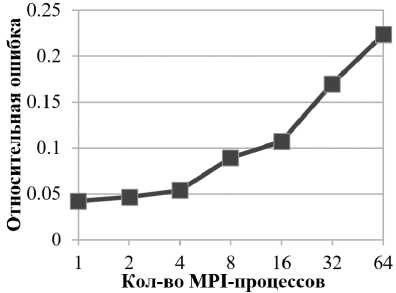
Предсказание времени работы проводилось для сетки размером 512x512x512. На рис. 7а представлены графики времени выполнения реального приложения, а также предсказанного времени выполнения при условии, что все обращения в память попадают в кэш L1 или в оперативную память. На рис. 7б представлена относительная ошибка предсказания времени выполнения при условии, что все обращения попадают в кэш L1. Из рисунка видно, что реальное время выполнения очень близко к предсказанному времени работы при попадании всех обращений в кэш L1. Исходя из этого, можно сделать вывод о том, что программа обладает хорошей локальностью обращений в память. Рост ошибки предсказания времени работы с увеличением количества процессов можно объяснить ростом погрешности в предсказании времени коммуникаций.

• а)    Реальное и предсказанное время работы

• б)    Относительная ошибка предсказания времени работы L1

Рис. 7. Измеренное и предсказанное время работы, а также относительная ошибка предсказания

Заключение

В статье представлено описание разрабатываемого подхода для прогнозирования динамических характеристик параллельных программ, основанного на статическом анализе исходного кода. Предлагаемый подход позволяет предсказывать значение таких характеристик параллельных программ, как число обращений на чтение и запись в память, число считанных и записанных в память байт, количество операций с плавающей точкой, размер отправленных и принятых по сети данных, а также время работы программы. Верификация предложенного подхода продемонстрирована на параллельной программе, моделирующей распространение волны в трехмерном пространстве. Относительная ошибка прогнозирования динамических характеристик составила менее 25%.

Дальнейшее направление исследований предполагает верификацию приведенного подхода на ВС с процессорами Intel и AMD, расширение подхода для предсказания энергопотребления, повышения точности предсказания коммуникационных расходов и работу с приложениями, использующими графические ускорители.

Работа выполнена при поддержке Российского фонда фундаментальных исследований (проект № 20-07-01053).