Stationary electrochemical machining simulation applying to precision technologies

The electrochemical machining (ECM) is widely applied in different industry fields, so, the investigation of electrochemical shaping is the problem of great interest [1-4]. For the purpose of machining precision increase the different technologies are used, which enlarge the dissolution localization. Passivating electrolytes and pulse ECM with vibrating electrode-instrument (ET) have been applied for this during the recent years. The using of short current impulses can also promote localization increase [5-7]. This recpiires the development of new mathematical models and solution of new problems statement.

1.    Localization Characteristic

For localization analysis of electrochemical machining the simulation problem of the processes taking place in special inter-electrode space (IES) is considered. IES consists of two parts [8] with different magnitude of inter-electrode gap S and S 1 (Fig. 1).

cathode anode

Fig. 1. Interelectrode space scheme

Every part represents a space filled with electrolyte. The voltage pulse of rectangular form is given on the electrodes, and electrochemical dissolution of anode material takes place.

The ECM simulation is based on the Faraday’s law, accordance to which the rate of electrochemical dissolution V ecm of machining surface (the anode) is equal to [9]

V ecm = kj k = KE / p,

where e is an electrochemical equivalent, p is a density of dissolved metal, j is a, current density on the anode boundary, к is an electrolyte conductivity, n = П ( j ) I^{s a} current efficiency (a part of current participating in the metal dissolution reaction).

The dependence of dissolution rate on current density (1) is also valid for the impulse ECM, but the proportionality coefficient k is decreased by a factor of Q, where Q is an impulse porosity.

It is important that the greater the relative velocities difference | A V_ecm| / V_ecm is at the different areas of IES, higher localization of the process takes place and the ET form is copied more accurately. Different factors as gas secretion on the electrodes surfaces, heating and impurity of electrolyte, electrode potentials variation and so on, affect the localization process.

Consider an ideal process when the anode and cathode potentials and n ^are constant magnitudes and gas secretion is absent. In this case

L 1

¹ dV ecm

V ecm

dS

S.

And now we consider the case

when the electrode potentials and current efficiency

are the functions of current density j. Then the current density is defined by the implicit function

. _ U ^- Ф ^{( j} ) ^{dj j к} S , dS

- S (¹⁺

κ dφ

S dj

Y

,

where ф ( j ) is an overall electrodes potential. S is an inter-electrode gap. U is a, voltage. In this case we find the relation similar to (2)

L 2 =

1 dV_ecm

V ecm

dS

-

1(1+ y

S η dj

1 +

κ

S

ddφj     .

It is convenient to use the ratio of (3) to (2) as a dimensionless parameter characterizing localization [8]

,   _ L 2 _ ( . ^j dn ) (. , ^кd Ф ) 1

^loc L 1           η dj S dj

.

It follows from (4) that the value k loc <  1 for n = const, dф / dj >  0, i.e. this process has smaller value of the localization coefficient than the ideal one. It means, that the rates difference of dissolution for such a process is smaller than for the ideal one. It requires the greater allowance for a prescribed copying accuracy. On the other hand, the value k loc >  1 for dn / dj >  0, ф = const. Therefore, the real dependences of the current efficiency and electrode potentials have an antipodal influence the localization coefficient.

The physical-chemical effects appear for commensurability of impulses duration with characteristic duration of capacity charges of the double electric layers of the electrodes surfaces and activation period. It has important premises for the copying accuracy increase. The dependences of the anode potentials on current density for the different impulse duration are shown in Fig. 2.

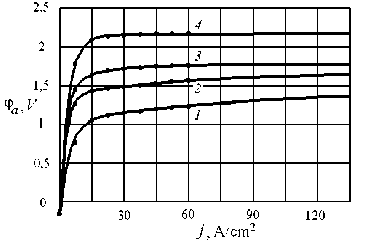
Fig. 2. Experimental dependences of the anode potential of chrome steel on current density under normal conditions in 8% water solution of NaNO3 are for different impulse duration t: 1-1 ^ s. 2-5 ^ s. 3 - 10 ^ s. 4 - 50 ^ s

The current efficiency is defined by following

n ⁽ j,ф a )=^{ П), Фа > Фа:a ®

The dissolution begins when the potential reaches some threshold value ф_с: , and the time that necessary for it depends on the local current density. So, dissolution begins later for a little current density that leads to the increase of the localization process.

2.    Current Efficiency Approximation and Main Assumptions

On the investigation ECM process the scheme of copying of hemispherical ET surface onto a plane billet surface is under consideration [8]. The scheme contains the most complex aspects of operations of electrochemical copying and it assumes the existence of convenient analytical solution. The ration of the value h/d (h is the hole depth, d is its width) to h i /d i for the ideal sphere segment is used as the parameter characterizing copying accuracy. One can see from Fig. 3 that there is optimal impulses duration for which the localization of the dissolution process is maximal.

The charge quantity is the same at the very experiment of spherical surface copying. The activating electrolyte (5% solution NaCl) is applied for the decrease of the current efficiency influence. The profiles and the appearance (enlarged by a factor of 25) of surfaces machined by the hemispherical ET are presented in Fig. 4.

The current efficiency dependence on current density n ( j ) is used for ECM simulation for consideration of various factors, influencing on the dissolution process and directly (as follows from (4)) determines the localization coefficient of the process. Thus, the steeper this dependence in working zone is, the higher the localization coefficient becomes. Now, we do not know a reliable method of theoretical determination of n ( j ) function. Thus, the experimental method of such dependences determination is appearing to be the most available (Fig. 5).

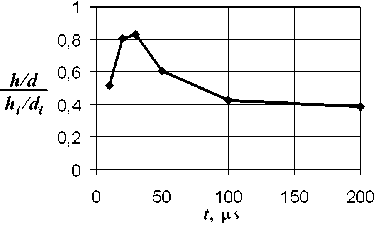
Fig. 3. Dependence of the copying accuracy on the current impulse duration

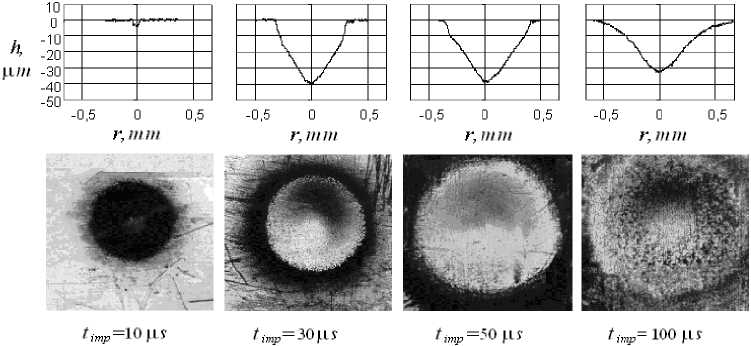
Fig. 4. Profiles and appearance of machined surfaces for different impulses duration t_imp

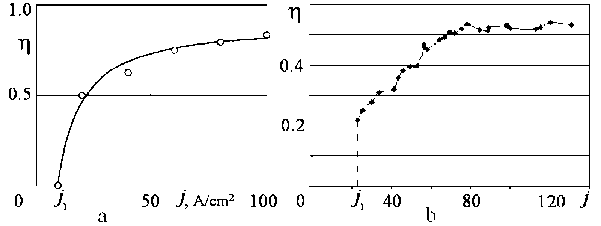
Fig. 5. Experimental dependences of the current efficiency on the current density obtained: a - from [10], b - from [11]

Previously, this dependence was approximated by a hyperbola [12], a quadratic-fractional function [13] or a piecewise linear function [14].

As it is shown above, at impulse duration about several microseconds in the beginning of the impulse the potential relaxation takes place and at this moment the dissolution of metal does not proceed. The experiment shows that in such machining method the regions of intensive and weak dissolution have more sharp borders.

In connection with it the dependence of current efficiency on the current density is modelled in [15] by the stepwise function

П ( j ) = <

η 0 ,

Vn е [о , П о ] , 0 ,

j > j 1 , j = j 1 , j < j 1 .

The similar model was used in [16].

Note, that that model (6) does not contradict the experimental data (Fig. 5), because the real dependence on passivating electrolytes contains the region of sharp change of current while the current density approaches to some threshold value j 1.

The most localization can be achieved if machining is realized for the current density closed to j 1 but exceeding this value, as it follows from (4).

In this case, the steepness of the dependence of current efficiency on current density according to (4) has more influence on the localization coefficient than the dependence on potential magnitude. Moreover, the determination of real dependences on electrode potentials represents a complex problem both theoretically and practically. In this connection the models with equipotential electrodes but taking into account dependence (6) are under consideration. These models describe the processes that have nearly maximum localization.

Let us assume that the impulses are rather short and there is no essential electrolyte heating and gas filling. In this case, the electrolyte is a uniform in space and time and methods of the theory of functions of a complex variable can be applied for the analysis process.

3.    ECM Stationary Model

Consider as an example the stationary shaping problem of the machining surface under cutting with a plate ET moving vertically downwards with a constant velocity Vet. It is supposed, that the machining surface ADB acquires the stationary form. The cross-cut of IES is shown in Fig. 6 a. The ET is presented as the cut ACB’. It is necessary to find the vector field of strength in IES and the shape of machining surface AFDGB.

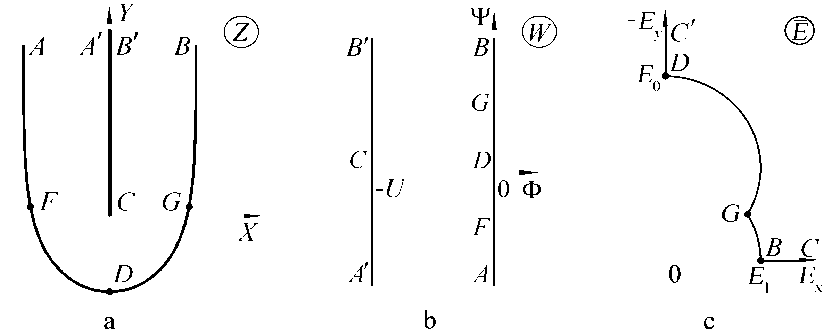
Fig. 6. The shape of IES domain: a - physical plane; b - complex potential plane; c -strength hodograph plane

Let Z = X /У. Consider a complex potential W = Ф + i T (Ф is a potential of electrical field, T is a stream function). The electric field strength is determined by the derivative

E=(2)- and the current density j = кЕ according to the Ohm’s low. Thus, the problem is reduced to the definition of the conform mapping of the IES domain of the physical plane onto domain of the plane W.

The potential Ф is considered to be constant on the boundary corresponding to ET and machining surface (Ф = —U on ET, Ф=0 on machining surface). The stream function Ф has a constant values on every streamline. That is why the domain corresponding to the IES on the complex potential plane is a vertical band (Fig. 6 b). As far as the machining surface is equipotential, the strength vector is a normal to the electrode surface at its every point.

The dependence of current efficiency on the strength is modeled by the stepwise function (6).

We consider only the right part of IES by virtue of its symmetry (Fig. 6 c). In this case the two domain are formed different types of boundary conditions on the machining surface. The first domain FDG, in which the strength exceeds Е 1 = j 1/ к because of proximity to ET, is characterized by the stationary condition [9] (by the equality of dissolution velocity V ecm and projection of the velocity V et on the normal to the machining surface) |E| = —Е 0 sin 6. where 6 is an angle of inclination of the strength vector to X -axis. Е 0 is the strength module at the point D. On the plane of strength hodograph Е = dW / dZ = |E| e -i a, circle arc witli the radius Е 0/2 and the ceriter at the point iE 0/2 corresponds to this section (Fig. 6 c). The magnitude Е 0 is determined from equality of the dissolution velocity condition to the ET movement velocity at the point D Е 0 = V et /( kn 0).

The second domain GB and the symmetrical domain AF are characterized by the constant strength modulo | Е | = Е 1. The circle arc of the radius Е 1 < Е 0 with the center at the origin of coordinate corresponds to this part on the plane Е.

On the boundary section BC corresponding to the ET surface the strength vector has an angle of inclination to the X -axis 6 = 0. The strength is in finite at the point C. Then a horizontal ray corresponds to this section on the hodograph plane. On the stream line CD 6 = —п/ 2. The vertical ray cor responds to it on the Е plane.

Let us introduce the parametric planes t 1 = Е 0/ Е and Z (the semi-ring). Their domains are shown in Fig. 7 a, b.

The function 1 1 ( Z ) is presented as a sum of the known function with given singularities, taking into account the solution properties, and the Laurent series

∞ t1 = —    Z + Edm (Zm — Z-m) •                     (')

m =1

We find W ( Z ) as

∞

W = W 0 + i^c m ( Z m — Z ^-m ) , m =1

w о = — in [ p L — ¹ ( —i vz. ) π ζ-p

where W 0 ( Z ) is the function mapping the semicircle of the plane Z onto the half-band of the plane W. For Z = P⁽"'

W 0 =      In (1 — p ² e i ) — in (2 ^p sin ^ ) .

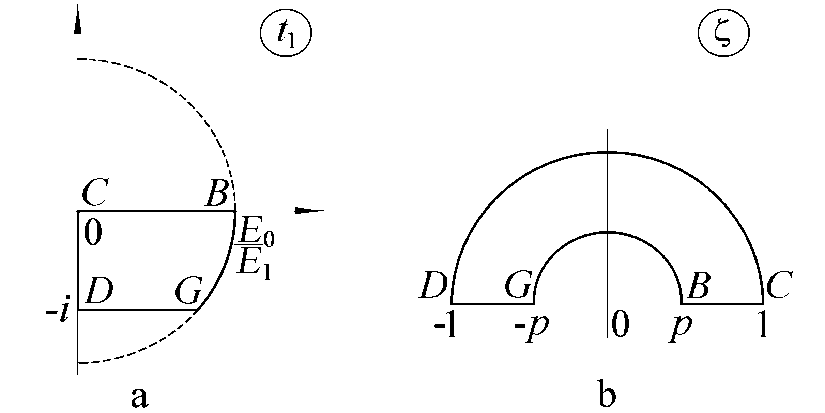
Fig. 7. The shapes of domains on the parametric planes t 1 and Z

Setting the imaginable part of (8) for Z — pem equal to 0 and expanding In (1 — p2cm) into Taylor series, we obtain cm

2 U 1    p2 m n m (pm + p-m)'

Thus

W — ^ [ln f 1 —pZi  ) + f 1 p    ⁽ Z m — Z -m )1

^{n      Z —} p        - =1 mp ^{m +} p ^-m

Let us find the derivatives dW/dZ and dZ/dW dW dζ

2 iU

π

-p

^{1 —} p^z

1        1

+ 2 Z ^— Z—p

^∞     2 m

+ 7 E mp m Zmm + -) ’ pm I p-m m=1

dZ _ 1 _ 1 1

dW ^— E ^— E 0 ’

Then

Z ( Z ¹ - / E W * - E.) [- П ¹" ^{Z 1} £ d m ^{( Z} - ^{— Z -}m )l dW*-     ^

m =1

The problem is reduced to the definition of the Laurent series coefficients d m (7) by the collocation method from the condition |t 1( pe i⁷ ) | — a — E ₀/ E 1 for 0 < о < n and numerical integration by formula (9) for calculation of machining surface shape. The points о_— — nm/ (2 n ) are chosen for this purpose and the system of nonlinear equations It 1 ( pe ^{i7 m} ) | — a, m — 1 ,..., n is formed and solved by the Newton’s method with step regulation.

4.    Numerical Results

The stationary surface shapes are presented in Fig. 8 a, where curves 0-6 correspond to a =l Д LL L3. L5. 2. 3. to. The scale unit is the magnitude S — U / E ₀. The dependence of front gap S f оn 1/ a — E 1 / E ₀ is shown in Fig. 8 b. Note, that the relation of the magnitude of lateral gap to the scale unit is equal to s l — S l / S — a.

The value of the front gap S f =0,49826686 for a =2 is obtained with high accuracy (about 8 decimal digits) for the comparison with solution results of other model problems.

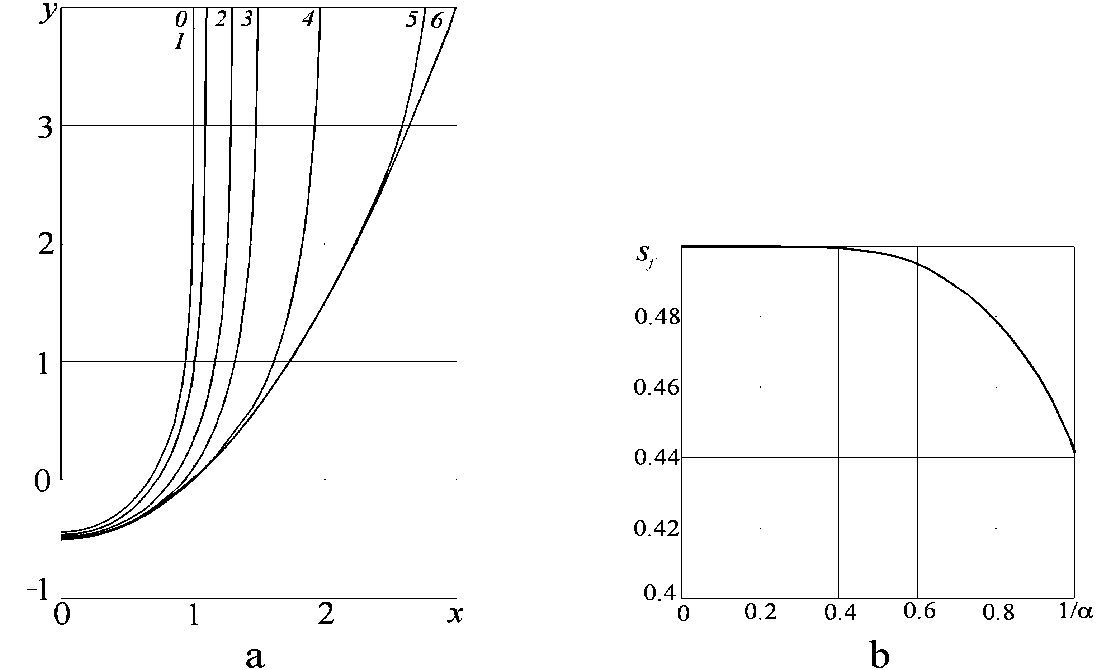
Fig. 8. The solution results: a - the machining surface shapes; b - the dependence of the front gap on the ratio 1 /a

For a ^ ж the whole machining surface is the stationary formation domain. In this case the solution is written as [9]

i ( W + U )² Z = - E_o   2 U  •

The lateral gap is equal to S f = 1/2.

For a ^ 1, on the contrary, the domain of the limiting formation | E | = E 1 occupies the whole machining surface and the limiting stationary solution is formed. It is given by [9]

Z = iU lncos П ( W + U ) , s, = 2ln2 « 0 , 4413 •

EE i 4 U             ^f n

Note, that limiting stationary mode differs from the ordinary limiting one as far as for stationary mode the IES shape is reserved at the coordinate system connected with moving FT.

Conclusion

The offered model of ECM with the stepwise function of current efficiency allows to shape the investigation for the highest localization of the dissolution process. The problems of stationary and limit-stationary ECM are formulated and solved for this purpose. The investigations show that the groove width which is formed as a result of cutting with the plate electrode tool significantly depends on ratio of maximum and critical values of electrical field strength on the anode surface. It is important for technology development of the precision electrochemical machining.

Acknowledgements. This work was financially supported by the Russian Foundation for Basic Research (Project code И-ОТООЗбб).