Статистическая оценка эффективности работы научного института

Наукометрические показатели применяются для оценки работы ученых в разных странах мира уже несколько десятков лет. В последние годы в научном сообществе сложилось мнение, что такие показатели не могут служить характеристикой качества работы ученого, но предоставляют оперативную информацию для выработки решения о финансировании научного проекта. Тем не менее поиск наиболее адекватных показателей качества труда отдельного исследователя продолжается (см., например, [1, 2]). В последние 15 лет в России предпринимаются методичные и последовательные попытки перестроить стиль работы российских ученых по общемировым стандартам. С начала 2007 года наукометрические показатели были внедрены в повседневную жизнь академических институтов России [3] и положены в основу стимулирования научной работы. Однако сразу проявились две главные проблемы — отсутствие адекватных показателей качества работы ученых, работающих в разных отраслях науки и практикующих разный стиль работы, и отсутствие единой шкалы показателей результативности коллективов научных учреждений, проводящих исследования по различным научным направлениям. Поэтому институтам РАН было предоставлено право выработать свою систему оценки результатов научной деятельности сотрудника. Были предложены различные схемы стимулирования научных исследований: от простейшей, предполагающей в своей основе экспертную оценку — выплаты ежемесячной фиксированной надбавки в заявительном порядке за публикацию единственной статьи в зарубежном научном журнале, находящемся по уровню рейтинга в квартилях Q1 или Q2 (НИУ «Высшая школа экономики» www. , до сложной формализо ванной, учитывающей множество показателей текущей деятельности сотрудника [4]. А по отношению к научным организациям были приняты методики оценки эффективности коллективов в рамках референтных групп по отраслям науки. Поэтому институты, относящиеся к разным группам, не подлежат сравнению. Как следствие этого для полидисциплинарных научных организаций, обладающих статусом юридических лиц, возникает проблема распределения финансирования, направленного на стимулирование отдельных обособленных структурных подразделений, показатели деятельности которых определены только в рамках своих референтных групп.

Целью данной работы является создание статистической модели научного института и разработка наукометрического показателя, не чувствительного к специфике научной отрасли, но позволяющего сравнивать публикационную активность научных коллективов.

Модель публикационной активности коллектива научных сотрудников

Несмотря на то, что весомость научного достижения нельзя отождествлять с формой представленного научному сообществу продукта научной работы, определенная связь между ними существует. Очевидно, что исследователь, получивший выдающийся результат, постарается опубликовать его в журнале с наибольшим импакт-фактором. Статья проходит экспертизу в редакции журнала и получает первичную оценку ее научного содержания. Поэтому факт опубликования научной работы в престижном журнале или любой другой вид апробации научных результатов, прошедший научную экспертизу (рецензирование), можно условно в рамках модели считать показателем качества научной работы данного исследователя.

Возьмем систему расчетов результативности условного академического института или отдельного обособленного структурного подразделения полидисци-плинарного научного центра, в которой учитывается максимальное количество видов апробации научных результатов — статей в журналах и сборниках, монографий, интернет-препринтов, патентов, ноу-хау, докладов на научных конференциях, атласов, карт, учебных пособий, компьютерных программ, патентованных методик и др. За основу формальных расчетов возьмем время, затрачиваемое на выполнение того или иного вида работы, итогом которой является данная научная продукция.

Введем ряд базовых понятий модели:

исследовательский проект — исследование, конечной целью которого является публикация или иной вид апробации полученного результата. Поскольку исследовательский проект направлен на создание публикации, то не будем разделять творческий исследовательский процесс и собственно написание научной работы;

продукт научной работы (единица научной продукции) — любой вид представленного научного результата отдельного исследовательского проекта: статья, доклад, монография, патент и т. д.;

показатель единицы научной продукции (Е j ) — число баллов, обозначающее условную «значимость» единицы научной продукции согласно принятой в данном коллективе формальной системе оценки;

период выборки (т) — период времени, за который производится текущая оценка публикационной результативности отдельного научного сотрудника и всего института;

показатель публикационной результативности научного сотрудника — сумма показателей всех произведенных им разнообразных единиц научной продукции за установленный период выборки:

П i = ^Е 1 ⁺ ^ 2 ⁺ " ⁺ k i , ⁽¹⁾ где k i — число единиц научной продукции, произведенных сотрудником за период выборки.

Число Е j представляет собой случайную величину, измеряемую в договорных баллах, определяемую статусом публикации, импакт-фактором издания, числом соавторов и положением данного исследователя в списке авторов. Учитывая разнообразие продуктов научной работы, можно понять, что она распределена в широком интервале — от нуля до большой, практически не ограниченной величины.

Важно отметить, что при условии широкого спектра учитываемых видов научных результатов и закономерно пересекающихся интервалов вариации их показателей согласно системе расчетов, а также с учетом отрасли науки и принятого в ней традиционного алгоритма проведения научных исследований формируется единый, весьма сложный для анализа непрерывный закон распределения случайной величины — Е j . Этот закон распределения, являющийся результатом договора в данном научном коллективе, является основным препятствием для проведения сравнительного анализа эффективности работы коллективов разных отраслей знания.

Примем следующие положения наукометрической модели:

• 1.    Выполнение исследовательского проекта занимает у произвольно взятого научного сотрудника заранее неизвестный объем рабочего времени.

• 2.    Отдельные научные проекты, завершенные публикацией, можно считать независимыми событиями, поскольку основные требования, предъявляемые к научной статье — ее целостность и завершенность — не предполагают дальнейшего продолжения.

• 3.    Результат отдельного исследования не дублируется в двух и более публикациях.

Таким образом, показатель публикационной результативности исследователя (1) за период выборки будет определяться суммой случайных величин в случайном числе.

Выполнение отдельного исследовательского проекта и создание соответствующей единицы научной продукции можно описать следующей статистической моделью.

Предположим, что исследователь, активно работающий к моменту t , продолжает работать и в момент t +А t . Пусть вероятность работы над проектом p зависит только от промежутка времени ( t , t +А t ). Кроме того, вероятность завершения работы над текущим проектом, продолжавшейся отрезок времени А t , пусть будет пропорциональна этой величине:

1 — p (А t ) = а А t .

Вероятность продолжения работы исследователя к моменту времени t +А t определится согласно теореме умножения вероятностей независимых событий как

p ( t + А t ) = p ( t ) • p (А t ) = p ( t )(1 — а А t ).

Отсюда в пределе при А t ^0 получим дифференциальное уравнение:

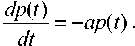
После интегрирования и выполнения нормировки вероятность работы над отдельным исследовательским проектом будет определяться зависимостью:

p ( t ) = exp(— at ). (2)

Описанная ситуация аналогична модели посещения покупателями небольшого магазина — время ожидания очередного посетителя для продавца не зависит от предыдущих ожиданий покупателей и распределено по показательному закону со средним значением t = 1/ а [5].

За установленный период выборки т количество независимых единиц научной продукции, опубликованных под авторством сотрудника данного института, составляет случайное число k i , подчиняющееся некоторому закону, который зависит главным образом от периода выборки и среднего времени работы над проектом. При этом важна стабильная кадровая структура института, средний многолетний стаж работы исследователей и устойчивость творческих традиций коллектива. Эти условия с учетом известной устойчивости структуры любой научной организации надежно выполняются в рамках 2-3-летних периодов выборки.

Численным моделированием легко установить, что относительная вероятность количества произведенных единиц научной продукции с затраченным на них временем, распределенным по закону (2), за фиксированный период выборки будет описываться распределением плотности вероятности, близким к непрерывному двухпараметрическому распределению Вейбулла (рис. 1):

/ ( x ) = nXx " ^-1 exp(— Xxⁿ ). (3)

Известно, что распределение Вейбулла представляет предельный случай распределений, описывающих

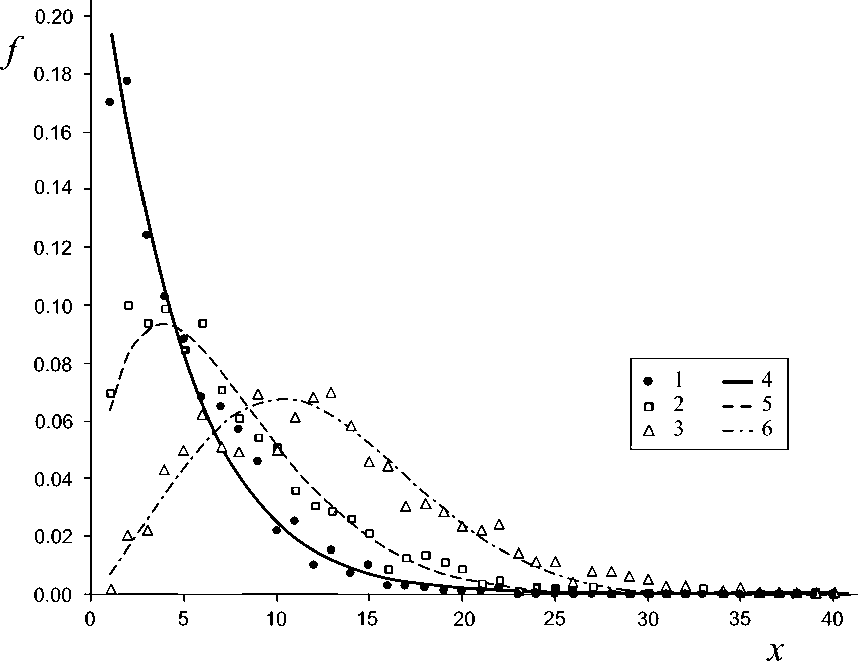
Рис. 1. Функция распределения числа апробаций исследовательских проектов научного сотрудника при параметре модели т а = 10 (точки 1), 25 (точки 2), 50 (точки 3). Объем расчетов методом Монте-Карло по каждой из трех серий — 1000. Полученные три серии данных приближены распределением Вейбулла (3) с параметрами n = 1.05, X = 0.216 (кривая 4), n = 1.5, X = 0.044 (кривая 5), и n = 2.2, X = 0.0033 (кривая 6). Непрерывная линия 4 практически совпадает с дискретным геометрическим распределением (4) с параметром q = 0.8 и носителем к = x

Fig. 1. The distribution function of the number of approbations of research projects of a researcher with the model parameter та = 10 (points 1), 25 (points 2), 50 (points 3). The volume of Monte Carlo calculations for each of the three series is 1000. The obtained three data series are approximated by the Weibull distribution (3) with parameters n = 1.05, X = 0.216 (curve 4), n = 1.5, X = 0.044 (curve 5), and n = 2.2, X = 0.0033 (curve 6). Continuous line 4 practically coincides with the discrete geometric distribution (4) with the parameter q = 0.8 and carrier к = x максимальный срок службы сложного технического изделия или устройства, состоящего из многих деталей со случайной наработкой на отказ [6]. Закон Вейбулла обладает важными свойствами: при параметре формы n = 1 он отображает экспоненциальное распределение, а при возрастании n становится похожим сначала на логнормальный, а затем на нормальный закон (рис.1) и в пределе при n^да стремится в дельта-функции. Моделированием установлено, что при среднем отрезке времени 1/а, затрачиваемом на создание единицы научной продукции на порядок меньше периода выборки (та =10), дискретное распределение числа единиц научной продукции весьма точно приближается к геометрическому распределению:

Pк ) = (1 - q ) q^{k -1} , (4) являющемуся аналогом непрерывного экспоненциального закона [6] (рис. 1, кривая 4).

В теории вероятностей известны предельные теоремы о сходимости функции распределения суммы случайного числа случайных слагаемых (теоремы переноса) [5]. В частности, в простейшем случае, при условии, что последовательность { k i } имеет геометрическое распределение (4), а параметр q стремится к 1, функция плотности вероятности суммы случайных слагаемых (1) сходится к показательному закону:

F ( x ) = (1/в) exp(- x /в). (5)

Применяя этот предельный случай для нашей модели, закон распределения показателя ^} для единицы научной продукции, регламентированный принятыми в конкретном институте правилами расчетов и спецификой научных исследований, не будет иметь значения для оценки публикационной активности сотрудников института. Это ключевой момент описываемой статистической модели.

Таким образом, проведя нормировку гистограммы распределения научных сотрудников института, предполагая, например, что общее число баллов составляет постоянную величину, можно воспользоваться законом (5), определяющим плотность вероятности нахождения итогового показателя публикационной результативности n i = x у случайно выбранного сотрудника.

Распределение (5) является аналогом равновесного распределения молекул газа по энергиям (распределение Л. Больцмана), в котором параметр в является показателем средней энергии молекулы, связанной с температурой системы. Таким образом, параметр в в (5) является аналогом «температуры», определяющей обобщенную публикационную активность коллектива научных сотрудников института. Поскольку данный параметр не чувствителен к закону распределения показателя отдельной научной продукции ^ ^ , то при условии выполнения описанных критериев расчета он позволяет сравнивать научные организации разных отраслей знания.

Можно предположить, что распределение (5), полученное на основании закона больших чисел и использованное для выборки показателей публикационной активности сотрудников института при соблюдении двух условий — т а = 10 и q ^1, будет наилучшим образом отражать текущий публикационный процесс в коллективе, в той или иной мере связанный с творческим процессом научных работников.

Показатели работы института естественно-научного профиля

Рассмотрим результаты работы сотрудников Института геологии Коми НЦ УрО РАН за два пересекающихся двухлетних периода: 2016—2017 и 2017—2018 гг. (рис. 2). Согласно разработанному в институте Положению о системе расчетов стимулирующих выплат [4] была принята достаточно сложная система учета множества видов научной продукции и факторов, влияющих на величину их показателя. В результате получены эмпирические распределения показателя результативности сотрудников (рис. 2), нормированные на фиксированную сумму в 100 баллов (выбор условия нормировки обусловлен удобством значения показателя эффективности, находящимся вблизи единицы). Оба распределения близки к экспоненциальному закону. Анализ первичных данных показывает, что среднее время, затрачиваемое на создание единицы научной продукции, в среднем по институту составляет чуть больше 2 месяцев, что соответствует условиям модели (т а ~ 10). В первый период в системе расчета показателей использовался закон равномерной плотности для расчета коэффициентов творческого участия соавторов коллективного труда, а во второй была применена более справедливая дифференцированная система расчета коэффициента творческого участия в коллективном исследовании.

Для расчета параметра в можно предложить следующий алгоритм:

• 1.    Выбирается произвольный интервал разряда по шкале нормированных баллов ( x, , x_{+ +1} ) и выполняется расчет относительной эмпирической вероятности попадания показателей публикационной результативности сотрудников в один из интервалов.

• 2.    Методом наименьших квадратов отклонений находится параметр в теоретического экспоненциального распределения вероятностей, максимально приближенного к эмпирическим данным. Суммирование квадратов разностей производится до максимального разряда, эмпирическая вероятность в котором не равна нулю.

• 3.    Изменяется интервал разряда и производятся новые расчеты по пунктам 1 и 2 до тех пор, пока сумма квадратов разностей теоретического и эмпирическо-

• Рис. 2. Нормированные функции распределения результативности сотрудников Института геологии за 2016—2017 (1) и 2017—2018 (2) гг. Линии отражают теоретические распределения соответственно для первой (3) и второй (4) выборок

  Fig. 2. Normalized distribution functions of the effectiveness of the staff of the Institute of Geology for 2016—2017 (1) and 2017—2018 (2). The lines reflect theoretical distributions for the first (3) and second (4) samples respectively

го распределений вероятностей по разрядам не достигнет минимума. Для удобства расчетов число разрядов должно находиться в интервале от 10 до 20.

Рассчитанные по данной методике параметры экспоненциальных распределений, аппроксимирующих две выборки результативности сотрудников института за 2016—2017 и 2017—2018 гг., составили 0.71 и 0.81. Повышение показателя в говорит о росте публикационной активности работы коллектива. В термодинамической системе аналогичное повышение температуры приводит к росту скорости химических реакций.

При высоких значениях баллов отмечаются видимые отклонения от теоретического закона, что связано с малой численностью научных сотрудников института (порядка 120 человек) и сильным влиянием высокого импакт-фактора журналов, в которых были опубликованы некоторые работы сотрудников. Использование дифференцированной шкалы расчета коэффициента творческого вклада в коллективной работе позволяет уменьшить величину отклонений. Для устранения недостатков системы расчета показателей можно предложить также отказаться от использования импакт-фактора журнала, заменив его распределением журналов по классам с логарифмической шкалой диапазонов. Кроме того, необходимо точно подбирать период выборки. Расчет оптимального периода выборки из условия т ~ 10/ а включает проверку соответствия функции распределения числа единиц продукции геометрическому закону распределения. Параметр q геометрического распределения (4) должен быть близок к 1.

Для научной организации, насчитывающей малое число сотрудников, расчеты можно выполнять по двум-трем последовательным периодам выборки, что позволяет формально «увеличить» число сотрудников вдвое-втрое. При этом ухудшается динамика показателя публикационной активности. Но есть и положительный момент: время подготовки публикации в научном журнале не будет сказываться на результатах расчетов.

Заключение

Таким образом, полученный экспоненциальный закон распределения публикационной активности научных сотрудников данного института при выполнении ряда описанных условий расчета представляет новый наукометрический показатель в — показатель публикационной активности научной деятельности коллектива (аналог термодинамической температуры), позволяющий сравнивать публикационную активность обособленных структурных подразделений между собой в рамках полидисциплинарных федеральных исследовательских центров и формально оценивать институты, выходя за рамки референтных групп.

В заключение заметим, что если при аттестации научных сотрудников или при их стимулировании будут преобладать формальные требования, регламентированные их должностными обязанностями, и не будет учитываться вклад сотрудника в тот или иной научный результат, хотя бы в соответствии с дифференцированной системой распределения коэффициента творческого участия в коллективном исследовательском проекте, количественные показатели, описанные в данной модели, согласно известному закону Гудхарта будут неизбежно превращаться в приоритетную цель.