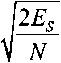Статистические характеристики обнаружения сигналов в дискретном времени при угломерно-корреляционном местоопределении источников радиоизлучения

* Corresponding author E-mail address:

Радиоэлектронная разведка является ключевым звеном в формировании информационной компоненты всестороннего обеспечения основных систем управления, что накладывает жесткие требования к возможному значению качественных показателей разведывательных средств, в частности, средств пеленгования и координатометрии. Одним из ключевых направлений исследований пространственного определения координат источников радиоизлучения является сокращение количества средств пеленгования в условиях воздействия дестабилизирующих факторов без потери качественных характеристик правильного обнаружения.

В [1] предложен способ определения координат излучающих радиоэлектронных средств, позволяющий снять ограничение на их пространственное размещение, а в [2, 3] – реализующий локализацию области пространства поиска за счет разрежения входного потока контактов на основе взаимного корреляционного анализа аддитивных сигнальных функций каждого из пространственно-разнесенных пеленгаторов. Вместе с тем в представленных работах не в полной мере рассмотрены вопросы расчета вероятностных характеристик обнаружения и различения сигналов при реализации дискретных методов обработки, осуществляемых указанным выше способом.

Проведение подобной оценки, учитывающей особенности пространственной нестабильности электромагнитных параметров среды распространения, инструментальных ошибок измерения фазы сигнала, возможно при использовании методов имитационного моделирования.

Основные результаты

Цель исследования – разработка имитационной модели угломерно-корреляционного поиска и координатометрии источников радиоизлучения, предусматривающей использование дискретных методов обработки и позволяющей провести оценку статистических характеристик обнаружения сигнала координатометрируемого источника в условиях воздействия дестабилизирующих факторов.

Исходя из особенностей способа триангуляционно-корреляционного местоопределения [3], структура модели должна представлять собой взаимосвязанные процедуры пространственного сканирования, пеленгования и координатометрии, а также статистического анализа результатов моделирования.

Рассмотрим особенности расчета вероятностных характеристик обнаружения и различения сигналов при реализации дискретных методов обработки.

Для рассматриваемого случая наблюдение осуществляется в дискретные моменты времени, реализация сигнально-шумовой функции представляет собой множество отчетов случайных величин { ξ ₁ } ^N – для ПС_1 и { ξ ₂ } ^N – для ПС_2. При этом будем считать, что элементы каждого из множеств определяются выборочными значениями принятых колебаний ξ 1 ( t ) и ξ 2 ( t ) каждой из пеленгаторных станций в моменты времени t ₀ ,…, t _i ,…, t _N-1 , взятых из интервала времени наблюдения T : ( t 1 ≤ t i ≤ t 1 + T ). Расстояние по временной оси между соседними отчетами примем одинаковыми, то есть Δ t = t _i – t _i-1 = const . Таким образом, для множества отчетов реализаций сигнально-шумовых функций имеем

{^ ={^,...U>X-Ut1.-A

{£ХНш).---.«ш.---.шч)),                          (1)

где / = 0^-1 – номер отчета; N = T · f д – количество отчетов; f д – частота дискретизации.

Учитывая дискретный характер наблюдения, структура корреляционного обнаружителя примет вид, представленный на рис. 1.

Согласно структуре корреляционного обнаружителя, гипотезам H 0 и H 1 соответствуют следующие значения функции η ( T )

И»: V (Г) = %(Г) = МХй('.)6('.)1 = / ^=0z=0

^-l км

MX (X s> ft)+«. ft ))(Хх- ft)+«=ft »(2)

z=0 k=lm=\

^,: У (П^АП^ЕйО^ЮЬ

/ ^7 = 0

^-l         Км

= ^(8,(1,)^^”^^^^,

7=0               ^=1777=1

где n ₁(₂) ( t _i ) = n ₁(₂)_{, i} – отчеты шума в дискретные моменты времени t _i .

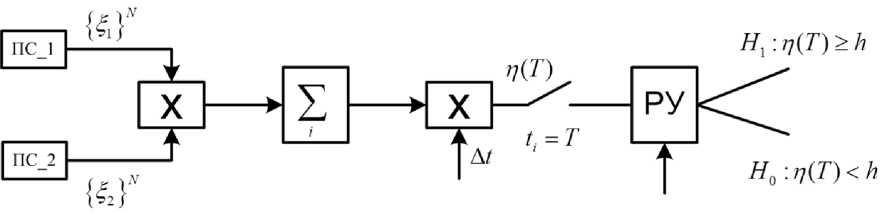
Рис. 1. Структура корреляционного обнаружителя, реализованного на дискретном множестве отчетов времени

Fig. 1. The structure of a correlation detector implemented on a discrete set of time reports

Здесь и далее будем считать, что дискретные отчеты шума являются независимыми случайными величинами, с совместной плотностью вероятности, характеризуемой следующей функцией:

) =

P^Q^^^i^^^N-l)  ( Г2 —) 11^7 ^ехр( 2 А 2     ).               (3)

,₌о             ,=0 2сг

С учетом того что математические ожидания и среднеквадратические отклонения распределений каждого из отчетов равны между собой и определяются следующими значениями:

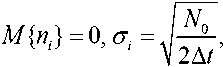
окончательно для совместной плотности (3) получим

^(77О,..., 77,.,... 77^ ) = (——) 2 ехр(- — ^ 77,2 ),

где N 0 – спектральная плотность мощности шума.

Существенным с точки зрения моделирования является вопрос формирования реализаций случайных флуктуаций шумовых функций n 1 ( t ) и n 2 ( t ) плотность, вероятность дискретных значений которых определяется соотношением (5).

В интересах решения данной задачи воспользуемся широко применяемым на практике подходом, предусматривающим функциональное преобразование реализаций равномерно распределенной на интервале [0,1] случайной величины, в соответствии с аналитической структурой функции распределения вероятности моделируемых реализаций [4]

{х^Г^ООПЯ^МО; 1], (6)

где F ^-1 ( y )– операция определения обратной функции.

Таким образом, применительно к закону распределения (5) для случайной величины, характеризующей значение шумового напряжения одного отчета дискретного множества значений, в соответствии с (6) получим следующее функциональное преобразование:

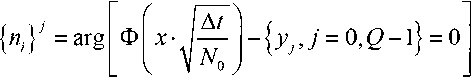
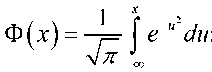
– количество элементов множества реализаций случайной величи- ны; y – множество реализаций равномерно распределенной случайной величины на интервале [0;1].

Немаловажным фактором при формировании статистической имитационной модели является обеспечение устойчивости результатов моделирования, которая фактически определяется множественным характером реализаций модели. Возникает задача определения достаточности статистических испытаний, при которой достигается требуемый уровень устойчивости результативного показателя.

С формализованной точки зрения приведенные выше условия определяются согласно следующему вероятностному критерию

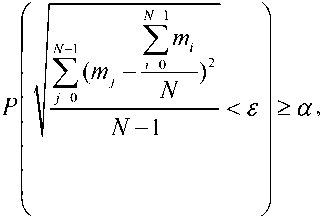
где ^mk

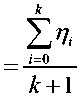
среднее значение корреляционного интеграла, рассчитанного для k + 1-ой ре- ализации; m = —   – статистическая оценка математического ожидания среднего значения

N корреляционного интеграла; д =

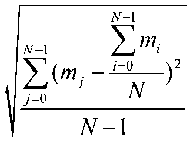
– среднеквадратическое отклонение вели-

чины среднего значения корреляционного интеграла; η j – значение корреляционного интеграла, рассчитанного для j – ой реализации; ε – величина доверительного интервала по значению среднеквадратического отклонения на множестве реализаций среднего значения корреляционного интеграла; α – требуемый уровень достоверности результатов моделирования.

На рис. 2 приведены графики зависимости среднего значения величины корреляционного интеграла, а также критериальных параметров, входящих в выражение (8), от количества реализаций имитационной модели.

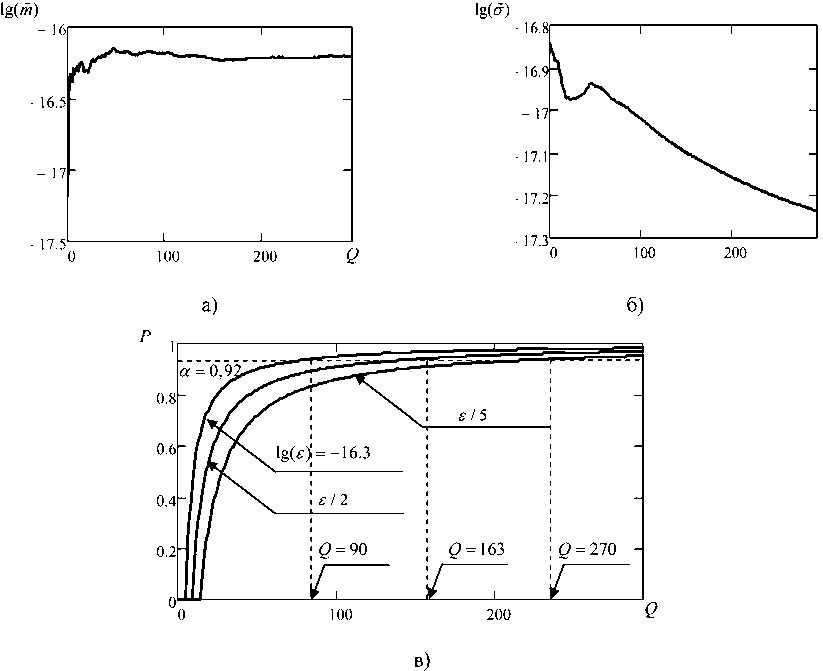
Рис. 2. Результаты оценки статистических показателей имитационной модели

Fig. 2. Results of the evaluation of statistical indicators of the simulation model

Представленные на рис. 2 зависимости могут быть использованы в интересах обоснования требуемого количества реализаций имитационной модели для достижения заданного уровня достоверности попадания среднеквадратического отклонения величины среднего значения корреляционного интеграла в доверительный интервал. Так, например, задаваясь уровнем достоверности сходимости среднего значения величиной α = 0,92, уменьшение значения доверительного интервала, определяемого по величине среднеквадратического отклонения в 2 раза, приводит к увеличению требуемого количества реализаций имитационной модели с Q = 90 до Q = 163.

Приведенные выше условия формирования параметров имитационной модели, которые характеризуются в том числе особенностями исходных данных, определяют необходимость включения в структуру модели элемента, обеспечивающего корректировку количества итерационных реализаций.

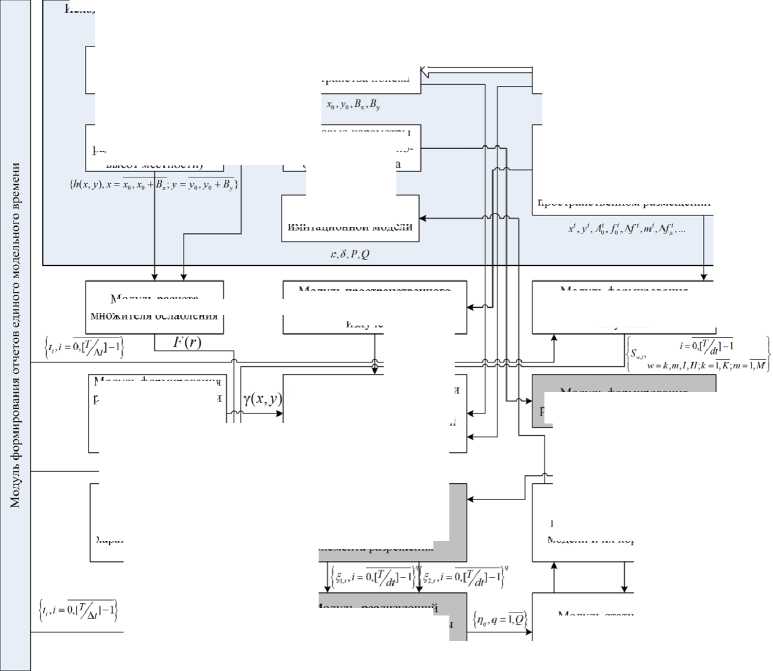
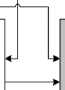
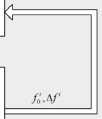
Структуру имитационной модели, обеспечивающей формирование статистического распределения корреляционного интеграла, определим в виде, представленном на рис. 3.

На рис. 3 серым цветом приподняты модули, реализация функций которых определяется количеством «прогонов» имитационной модели ( Q ).

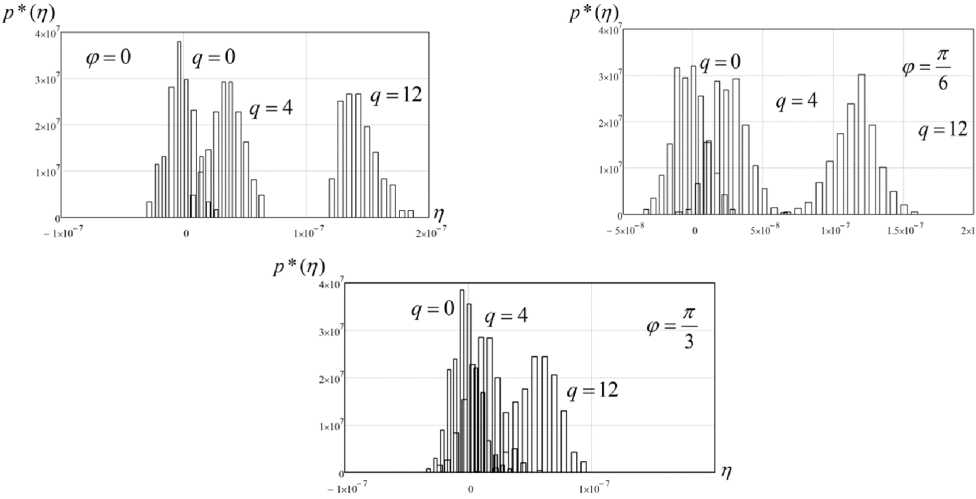
Полученное на основе имитационного моделирования статистическое распределение величины корреляционного интеграла p ^* ( η ) применительно к различным условиям моделирования, характеризуемым наличием ( θ = 1) либо отсутствием ( θ = 1) сигнала источника излучения, – 945 –

Исходные данные моделирования

Размер элементов

Высотные параметры радиотрассы (матрица высот местности)

Электромагнитные параметры радиотрассы

Параметры сигналов источников излучения и координатометрические данные об их пространственном размещении

Модуль расчета множителя ослабления

Модуль формирования сигналов источников излучения

Модуль, реализующий вычислительные процедуры оценки корреляционной функции

Рис. 3. Структура имитационной модели

Модуль формирования разрежающей функции для реализации алгоритма сканирования ____

Координаты области [ д разрешения пространства поиска

Шумовые параметры ат мосферы и антенно фидерного тракта

Параметры имитационной модели

Модуль пространственного распределения источников излучения

Модуль сканирования области пространства поиска и настройки на анализируемый элемент разрешения

Модуль формирования реализаций шумовой функции

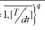
Модуль расчета энергетических характеристик сигнала

Модуль формирования реализаций сигнальношумовой функции для элемента разрешения

Модуль определения параметров имитационной модели и их корректировки

Параметры антенной решетки, реализующей функции амплитудного сканирования R^J^e^N

Модуль статистической обработки результатов моделирования

Модуль определения вида закона распределен ия и оценки СХОДИМОСТИ

• Fig. 3.    Structure of the simulation model

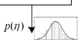
анализируемого элемента пространственного разрешения, позволяет оценить величину вероятности правильного обнаружения P _D . В интересах оценки последней воспользуемся следующим соотношением:

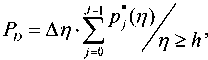
где J = [5·lg Q ] – количество интервалов статистической оценки плотности вероятности распределения величины корреляционного интеграла; [•] – операция определения целой части; Δ η – величина интервала изменения корреляционного интеграла, применительно к которой рассчитывается частота события Pj^ попадания реализаций η _i в пределы области [ η j , η j + Δ η ).

Для расчета частоты события Pj^ и, соответственно, статистической плотности вероятности воспользуемся выражениями вида

ЁМ ^^ <[% +А?7])*0}

Р^) = ----------- Я-----------’                              (10)

В соотношении (9) h – величина порога принятия решения о наличии сигнала источника, расположенного в анализируемом элементе разрешения, определение которого осуществляется на основе критерия Неймана-Пирсона в соответствии с выражением

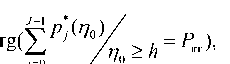
где P _лт – вероятность ложной тревоги.

Приведенные выше соотношения позволяют, опираясь на результаты статистической оценки величины корреляционного интеграла, определить качественные показатели обнаружения сигнала в элементе разрешения применительно к различным пространственным и энергетическим условиям.

Для проведения вычислительного эксперимента в качестве модели сигнала рассмотрим амплитудно-модулированный сигнал, параметры которого, такие как амплитуда, несущая частота, частота модулирующего колебания и глубина модуляции, могут изменяться.

Математические модели сигналов первого ( I ) и второго ( II ) пеленгаторов определим в следующем виде:

^ (?) = Л[1 + ти cos( 2 л’Р?)] cos( 2 л^- ft +

0)

S_n(t) = ct41+mcos(2s'R)]cos(2ff/? + (j₀ +

,

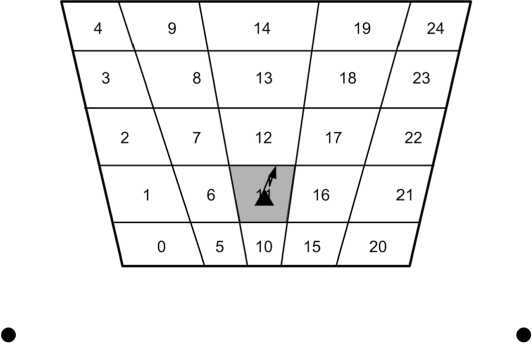
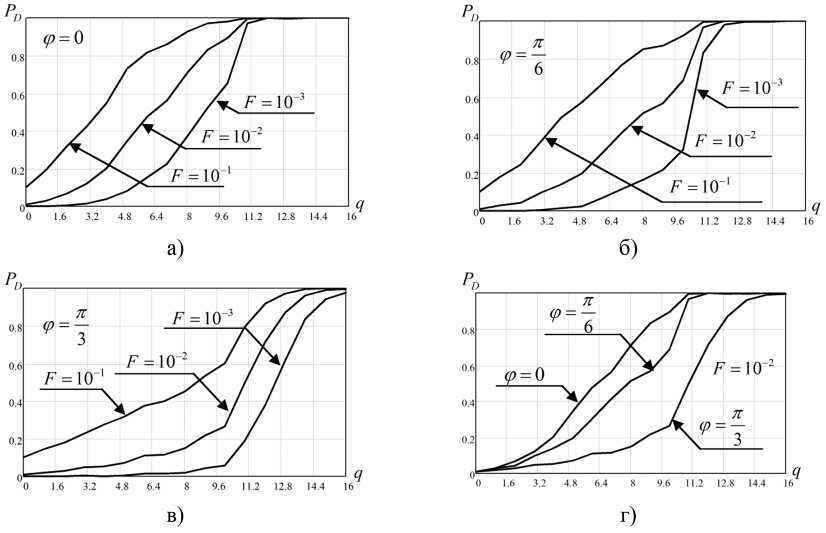
где α – амплитудный множитель; φ – случайное фазовое рассогласование.

Возникновение фазового рассогласования, имеющего случайный характер, обуславливается в первую очередь уникальными особенностями распространения радиоволн на радиотрассах, источник излучения – ПС_1 и источник излучения – ПС_2, а именно влиянием высотно-неоднородного и электромагнитно-неоднородного характера среды распространения на амплитуду и фазу напряженности поля волны. В частности, стохастические флуктуации диэлектрической проницаемости тропосферы приводят к случайным изменениям фазы поля волны, что в конечном итоге, в силу их статистической независимости на различных участках радиотрассы, приводит к возникновению фазового рассогласования. Более подробное обоснование параметров статистического распределения рассогласования фаз, характеризуемого приведенными выше обстоятельствами, представлено в [5].

На рис. 4, 5, 6 приведены результаты моделирования в виде статистических плотностей вероятности распределения величины корреляционного интеграла η для различных значений соотношения сигнал/шум (q), а также зависимости вероятности правильного обнаружения от q при различных значениях величины фазового рассогласования.

Выводы

Анализ полученных в работе зависимостей показывает, что увеличение фазового рассогласования приводит к уменьшению вероятности принятия правильного решения о наличии в анализируемом элементе разрешения источника излучения, причем эта зависимость суще-

Рис. 4. Геометрические условия взаимного пространственного размещения пеленгаторов и источника излучения

• Fig. 4.    Geometric conditions of mutual spatial arrangement of direction finders and radiation source

  

  Рис. 5. Статистическая плотность вероятности распределения величины корреляционного интеграла η для различных значений соотношения сигнал/шум

  
  

• Fig. 5.    Statistical probability density function of the distribution of the magnitude of the correlation integral η for different values of signal-to-noise ratio

  ственно не линейна, в частности, при

  
  
  
  
  

  = 5 изменение фазового рассогласования с φ = 0 до

  
  

V = - вызывает изменение вероятности на величину ΔPs = 0.05, изменение же рассогласования

7Г           ТС с <р=- до <р=- – ΔPs = 0.18 (рис. 6г).

6         3

Таким образом, в настоящей статье предложена структура и на ее основе разработана ком- пьютерная имитационная модель процесса угломерно-корреляционной координатометрии источников излучения, предусматривающей реализацию корреляционной обработки сигналов

Рис. 6. Зависимости вероятности правильного обнаружения от соотношения сигнал/шум для различных условий моделирования

Fig. 6. Dependences of the probability of correct detection on the signal-to-noise ratio for different modeling conditions пеленгаторных станций на дискретном множестве отчетов времени. Модель позволяет провести статистический анализ параметров обнаружения координатометрируемого источника в элементе пространственного разрешения. Результаты моделирования могут быть использованы в интересах обоснования пространственных параметров угломерно-корреляционной системы местоопределения, а также требований к направленным свойствам антенных систем пеленгаторов.