Статистические исследования точности высотного положения покрытий автомобильных дорог
Автор: Пронина Л.А., Мадиев А.Г.
Журнал: Вестник Омского государственного аграрного университета @vestnik-omgau
Рубрика: Технические науки
Статья в выпуске: 1 (29), 2018 года.
Бесплатный доступ
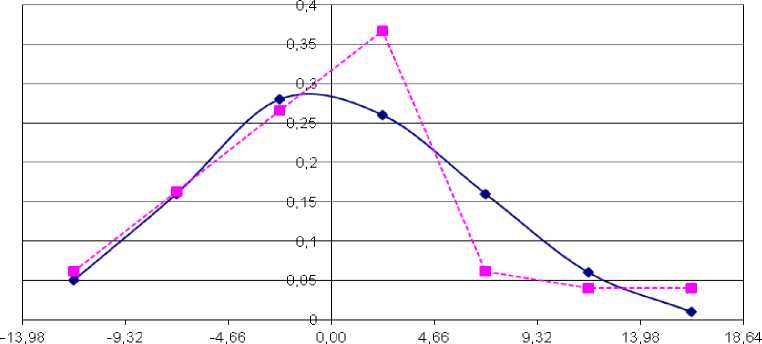
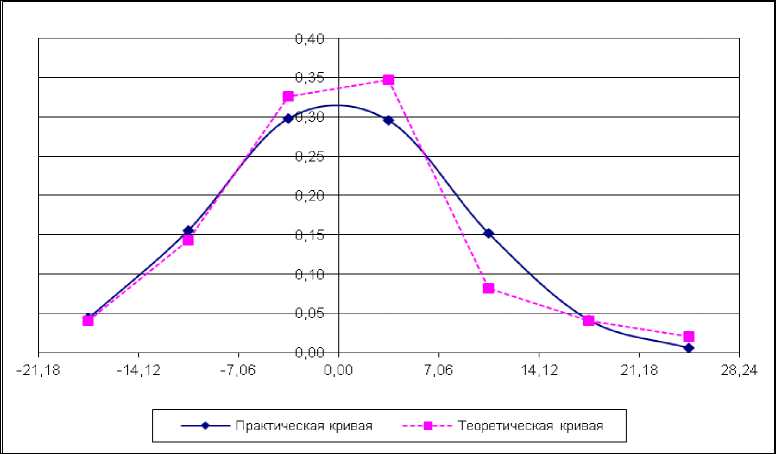
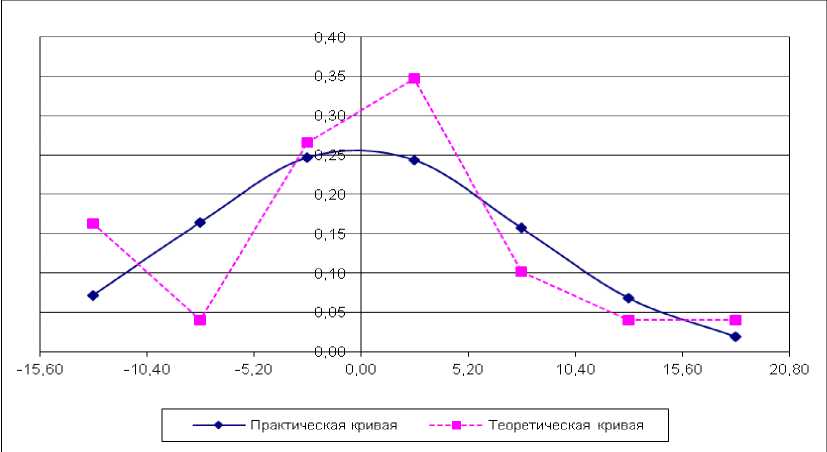
Представлен обзор и анализ работ, направленных на производство нивелирования при возведении автомобильных дорог, приведен статистический анализ эмпирических данных. Проанализированы нормативные документы по строительству и приемке в эксплуатацию линейных сооружений на примере автомобильных дорог. Рассмотрена методическая основа статистических исследований и выполнено исследование ровности поверхности верхнего слоя асфальтного покрытия километрового участка автомобильной дороги в деревне Кокшенево Муромцевского муниципального района Омской области. Нивелирование участка автомобильной дороги выполнено с применением электронного тахеометра с шагом нивелирования 20 м, в результате получены абсолютные высоты. По ним вычислены амплитудные разности высот, с их использованием проверены результаты статистического анализа на нормальное распределение эмпирических значений. По результатам статистического анализа - точечная и интервальная оценка точности с вероятностью Р = 0,95. Построены графики практического и теоретического распределений амплитудных разностей высот асфальтного покрытия автомобильной дороги по ее оси, левой и правой кромкам. Вычислены критерии Пирсона и Ястремского, подтверждающие нулевую гипотезу о нормальном распределении амплитудных разностей высот. Установлено, что амплитудные разности высот поверхности асфальтного покрытия соответствуют требованиям документа СНиП 3.06.03-85, регламентирующего строительство автомобильных дорог, и не превышают 24 мм (дороги I, II и III категории с применением комплектов дорожных машин без автоматической системы задания высот). Полученные результаты показывают, что при строительстве автомобильной дороги был налажен технологический процесс производства работ для обеспечения ее заданного положения в высотном отношении.
Автомобильная дорога, высоты, амплитудные разности высот, точность, асфальтное покрытие, высотное положение
Короткий адрес: https://sciup.org/142213489
IDR: 142213489 | УДК: 625.72:528.486
Текст научной статьи Статистические исследования точности высотного положения покрытий автомобильных дорог
Автомобильные дороги являются линейными сооружениями, необходимыми для обеспечения населения страны путепроводными артериями, без поддержания, развития и совершенствования которых невозможен подъем экономики области и страны в целом. Строительство таких объектов должно выполняться с высокой точностью, чтобы сооружение прослужило долго и соответствовало нормам, изложенным в стандартах (ГОСТах), СНиП, СП и проектно-конструкторской документации. Некачественное выполнение работ по строительству автомобильных дорог может привести к преждевременному выходу из строя транспортных средств и самого линейного сооружения.
В ранее действующих документах, регламентирующих возведение автомобильных дорог, приведены величины предельных погрешностей выполняемых работ. Например, невязка двойного нивелирного хода длиной L (км) при передаче высот допускалась 50√L, мм, в этом случае необходимо прокладывать ход технического нивелирования. Подобные рекомендации были и остаются при возведении линейных объектов в учебной литературе для выполнения геодезических работ. Например, в учебнике для студентов высших учебных заведений [1] невязка в ходе между реперами, высоты которых известны, не должна превышать 50√L, мм, где L ‒ длина в км. В учебниках и учебных пособиях для студентов высших учебных заведений других авторов [2], [3], [4] и [5] также приведены рекомендации. При этом ход технического нивелирования прокладывался с применением нивелира Н-3. С течением времени требования норматив-
ных документов, регламентирующих строительство автомобильных дорог, изменяются, как и инструментальная база приборов в производстве строительного процесса.
Исследование опытных зависимостей для связи характеристик продольной и поперечной ровности с параметрами изменения дорожного сооружения рассматриваются в работе [6]. Кроме того, приведены результаты экспериментальных исследований изменения высотного положения конструкции сооружения под влиянием многократных нагрузок.
Точность строительства автомобильных дорог, позволяющая обеспечить их ровность, ‒ один из основных показателей современного строительства [7]. Предельные допустимые значения амплитудных разностей высот для различных категорий дорог при нивелировании с шагами 5, 10 и 20 м регламентировались на время строительства дороги СНиП 3.06.03-85 [8], а в настоящее время СП 78.13330.2012 [9]. В разделе «Приемка выполненных работ» этих нормативных документов для определения ровности приведены предельные значения при нивелировании с шагами 5, 10 и 20 м.
В статье рассмотрены статистические исследования точности ровности поверхности асфальтного покрытия километрового участка автомобильной дороги в деревне Кокшенево Муромцевского муниципального района Омской области, построенной в 2013 г. в соответствии с СНиП 3.06.03-85 [8], при шаге нивелирования 20 м. Статистическими данными являются амплитудные разности высот, полученных по результатам нивелирования.
Материалы и методы
На верхнем слое асфальтного покрытия автомобильной дороги в деревне Кокше-нево протяженностью 1 км было выполнено нивелирование оси, левой и правой кромок с использованием электронного тахеометра. По результатам нивелирования получены высоты поверхности асфальтного покрытия автомобильной дороги и вычислены значения амплитудных разностей высот по формуле (1) согласно [8].
^ H . = H i 2H '
—
H i + 1 ,
где H i , H i+1 , H i+2 – высоты соседних точек.
На основе значений амплитудных разностей высот в статье выполнена математическая обработка статистических исследований ровности поверхности асфальтного покрытия автомобильной дороги; установлена закономерность распределения амплитудных разностей высот. Для проведения исследований рассчитана интервальная разность h ряда по формуле (2) согласно методике, приведенной в работе профессора Ю.В. Столбова [10].
R h =-------------,
1 + 3,32lg N где R – размах варьирования амплитудных разностей высот; N – количество амплитудных разностей высот.
Размах варьирования значения амплитудных разностей высот от максимального к минимальному определен по формуле
R = ( x max
x min ) ,
где x min и x max – соответственные варьирующие значения амплитудных разностей высот.
Число интервалов в ряду амплитуд позволяет определить формула к = Rh. (4)
За начало первого интервала принято значение хтч = ( х ^ - к /2 ) .
Величины, характеризующие количественную характеристику появления значений x i в интервале, называются частотой и обозначаются n , а их отношение к общему числу выбранных значений наблюдений принято называть частостями, их вычисляют согласно [10] из отношения
Wt = nt / N . (5)
Набор интервалов и их частоты составляют статистическое распределение ряда амплитудных разностей высот. Частотой интервала характеризуется сумма частот амплитудных разностей высот, попавших в интервал, при этом сумма всех частот вариационного ряда равна их количеству в нем.
За количественное значение, вокруг которого группируются значения
амплитудных разностей x 1 , x 2 , x 3 ,
..
., x n величины х , принята средняя арифметическая
ряда, эта характеристика статистической оценки определяется формулой N
Е nx
X = —--
N
,
где N – количество амплитудных разностей высот; n i ‒ частота; x i – середины интервалов вариационных рядов.
Простейший количественный признак вариации наблюдаемых значений ряда относительно своего среднего значения x характеризуется дисперсией Д и стандартом σ, эти характеристики устанавливают по формулам: k
Е n i •( х - х )2 д =—------
N
,
(Г =
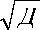
Пользуясь «исправленным» средним квадратическим отклонением (СКО) можно вычислить значение среднеквадратической погрешности (СКП) определения амплитудных разностей высот согласно [10] по формуле
m =
2 nz ( х х ) ;
i = 1 _______________
N1
По величине СКП, пользуясь формулой (10), рассчитывается величина М ‒ СКП среднего арифметического значения ряда амплитудных разностей высот. Величина СКП самой СКП ‒ m ‒ может быть вычислена по формуле (11)
m
м = ^ ;
N
m mm 42(N 1) '
Предложенная по формулам (2)‒(11) оценка точности является точечной и определяется одним числом. В статье рассматривается интервальный ряд с максимальным и минимальным значениями амплитуд высот, поэтому в данном случае следует
использовать интервальные оценки. Интервальная оценка точности подразумевает определение двух значений, характеризующих как точность, так надежность полученных оценок [10].
Для оценки среднего значения амплитудных разностей высот X и СКО, или дисперсии, нами применен метод «доверительных интервалов». Для определения границ доверительных интервалов использованы точечные характеристики X и т, доверительная вероятность P = 0,95 и уровень значимости (точность оценки) q = 0,05 . При построении доверительных интервалов с доверительной вероятностью P = 0,95 учитывается, что появление значений амплитудных разностей высот, превышающих по абсолютному значению величину, равную 2 т , будет минимальным и исследуемые интервальные ряды имеют ограниченный объем.
Для математического ожидания а и стандарта а в пределах интервального ряда доверительные интервалы будут иметь вид x —t • m / .N < a < x +t • m 1JN, (12)
m — t • mФ • ( N - 1 ) < a < m + 1 • m /V 2 • ( N - 1 ) , (13)
где t - коэффициент перехода от предельных значений к СКП, определяемый из таблиц [11], [12] по доверительной вероятности P = 0,95 и количеству амплитудных разностей высот N.
Методика оценки для определения доверительных интервалов для математического ожидания а и стандарта а справедлива при числе амплитудных разностей высот N > 50. В результатах исследований используется ограниченный интервальный ряд, состоящий из 49 амплитудных разностей высот, поэтому для оценки математического ожидания применяется распределение Стьюдента и в неравенство (12) вводится коэффициент t - нормируемый множитель, который заменяет коэффициент t и зависит как от доверительной вероятности Р = 0,95, соответствующей выполнению геодезических работ, так и от количества амплитудных разностей высот в ряду. Доверительный интервал в этом случае для оценки математического ожидания запишется в виде x — t ■ т I 4N < a < x + t • т 1XN. (14)
Доверительный интервал для оценок стандарта а с применением распределения критерия Пирсона х 2 с N - 1 степенями свободы будет определяться неравенством т (1 — g )<^ < т (1 + g), (15)
где т - СКП амплитудных разностей высот; g - коэффициент, выбираемый по таблицам [11], [12] и зависящий от объема вариационного ряда и вероятности.
Результаты исследований
Статистическая обработка амплитудных разностей высот асфальтного покрытия автомобильной дороги по оси выполнена с использованием формул (2)‒(9), приведена в табл. 1, по левой кромке - в табл. 2, по правой кромке - в табл. 3, доверительные интервалы, рассчитанные по формулам (14)-(15), приведены ниже указанных таблиц.
Таблица 1
|
Интервалы, мм |
Часто-та, n i |
Частость, W i |
Середина интерв. xi , мм |
nx i ,, мм |
х - x, мм |
n i ( х i - x ), мм |
n i (x i - x )2, мм |
t1 |
t 2 |
1 Ф ( t 1 ), |
1 Ф ( t 2 ), |
P(x i ) |
|
|
a |
b |
||||||||||||
|
‒13,98 |
‒9,32 |
3 |
0,06 |
‒11,65 |
‒34,95 |
‒11,89 |
‒35,66 |
423,96 |
‒2,33 |
‒1,57 |
‒0,49 |
‒0,44 |
0,05 |
|
‒9,32 |
‒4,66 |
5 |
0,10 |
‒6,99 |
‒34,95 |
‒7,23 |
‒36,14 |
261,20 |
‒1,57 |
‒0,80 |
‒0,44 |
‒0,29 |
0,15 |
|
‒4,66 |
0 |
16 |
0,33 |
‒2,33 |
‒37,28 |
‒2,57 |
‒41,08 |
105,49 |
‒0,80 |
‒0,04 |
‒0,29 |
‒0,02 |
0,27 |
|
0 |
4,66 |
18 |
0,37 |
2,33 |
41,94 |
2,09 |
37,66 |
78,79 |
‒0,04 |
0,73 |
‒0,02 |
0,27 |
0,28 |
|
4,66 |
9,32 |
3 |
0,06 |
6,99 |
20,97 |
6,75 |
20,26 |
136,78 |
0,73 |
1,49 |
0,27 |
0,43 |
0,16 |
|
9,32 |
13,98 |
2 |
0,04 |
11,65 |
23,30 |
11,41 |
22,82 |
260,48 |
1,49 |
2,25 |
0,43 |
0,49 |
0,06 |
|
13,98 |
18,64 |
2 |
0,04 |
16,31 |
32,62 |
16,07 |
32,14 |
516,63 |
2,25 |
3,02 |
0,49 |
0,50 |
0,01 |
|
Сумма |
49 |
1,00 |
11,65 |
1783,34 |
|||||||||
Статистическая обработка амплитудных разностей высот асфальтного покрытия автомобильной дороги (ось дороги)
x = 11,65/49 = 0,24 мм М = 6,10/749 = 0,87 ммm = 71783/48 = 6,10 мм mm = 6,10/72 (49 - 1) = 0,62 мм
Список литературы Статистические исследования точности высотного положения покрытий автомобильных дорог
- Геодезия: учебник для студ. высш. образ./Е.Б. Клюшин ; под ред. Д.Ш. Михелева; 12-е изд., стер. М.: Академия, 2014. 496 с.
- Маслов А.В., Гордеев А.В., Батраков Ю.Г. Геодезия: учебник. М.: Колос, 2013. 598 с.
- Чекалин С.И. Основы картографии, топографии и инженерной геодезии: учеб. пособие для вузов; 3-е изд., перераб. и доп. М.: Академический проект, 2013. 319 с.
- Буденков Н.А., Нехорошков П.А., Щекова О.Г. Курс инженерной геодезии: учебник/под общ. ред. Н.А. Буденкова; 2-е изд., перераб. и доп. М.: Форум: Инфра. М., 2014. 272 с.
- Дьяков Б.Н., Ковязин В.Ф., Соловьев А.Н. Основы геодезии и топографии: учеб. пособие . СПб.; М.; Краснодар: Лань, 2016. 272 с.
- Gercog V.N., Dolgikh G.V., Kuzin N.V. Calculation criteria for road pavement evenness. Part 1: substantiating the flatness standards of asphalt concrete pavement//Magazine of Civil Engineering. 2015. No. 5 (57). Pp. 45-57.
- Столбов Ю.В. . Исследование точности высотного положения верхнего слоя покрытия автомобильной дороги с шагом нивелирования десять метров//Вестн. СибАДИ. 2012. Вып. 6 (28). С. 73-77.
- СНиП 3.06.03-85. Автомобильные дороги. Госстрой СССР. М.ЦИТП Госстроя СССР, 1985. 106 с.
- СП 78.13330-2012. Актуализированная редакция СНиП 3.06.03-85. Автомобильные дороги. М.: Минрегион России, 2012. 118 с.
- Столбов Ю.В. Основы расчета и анализа точности возведения сборных зданий и сооружений: учеб. пособие. Омск, 1981. 64 с.
- Вентцель Е.С., Овчаров Л.А. Теория вероятностей и ее инженерное приложение: учеб. пособие для студ. втузов; 3-е изд. перераб. и доп. М.: Академия, 2003. 464 с.
- Гмурман Е.В. Теория вероятностей и математическая статистика: учебник для вузов. М.: Высшая школа, 1977. 479 с.