Статистический анализ и моделирование данных в MATLAB

На практике входные сигналы радиотехнических систем (РТС) содержат случайные помехи и шумы. Например, в отсутствие полезного сигнала на входе приёмника действует напряжение, уровень (амплитуда) которого описывается Рэлеевским законом распределения. Наличие этого напряжения обусловлено тепловым шумом приёмных трактов. В условиях многолучевого распространения радиосигнала [1] его уровень на входе приемника меняется случайным образом, а закон распределения амплитуд в данном случае (при отсутствии прямой видимости между передатчиком и приемником) – также является Рэлеевским. В связи с этим, задача оценки статистических параметров входных воздействий, а также их моделирование для проверки функционирования РТС – всегда остается актуальной.

Цель работы – показать, на примере программной среды MATLAB, последовательность действий для эффективного и ёмкого статистического анализа и моделирования входных данных сложных РТС.

На основании выборки входных данных производится построение гистограммы. Делается предположение о виде распределения. Оцениваются основные статистические параметры. Выбирается алгоритм формирования случайных чисел, строится гистограммы сформированной выборки случайных чисел. Производится анализ адекватности полученной модели по критерию хи-квадрат.

Экспериментальные данные

Выборка входных данных, подлежащая статистическому анализу и синтезу на ее основе статистической модели, представлена одномерным вектором вещественных чисел. Набор чисел представляет собой 500 нормированных экспериментальных измерений уровня сигнала на входе приемника в отсутствие иных сигналов в эфире, т. е. представлены измерения флуктуаций теплового шума.

На рисунке 1 представлена гистограмма, построенная по входной выборке данных в программной среде MATLAB с помощью встроенной функции histogram() [5].

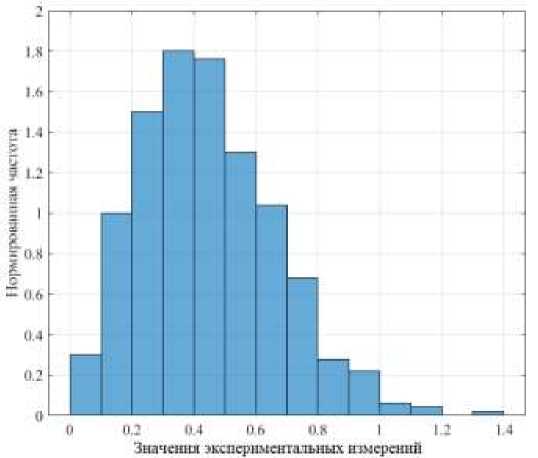
Рис. 1. Гистограмма экспериментальной выборки данных (N=500)

По горизонтальной оси откладываются значения экспериментальных измерений, по вертикальной – нормированная частота появления значений выборки. Всего в гистограмме 15 столбцов, идущих от 0 до 1.5 с шагом 0.1.

Статистический анализ данных

По виду гистограммы, представленной на рисунке 1, необходимо сделать эмпирическое предположение о виде распределения. В данном случае можно утверждать, что распределение является Рэлеевским. Функция плотности вероятности (ФПВ) такого распределения будет определяться следующим выражением (1):

f(x) = —?e 20-2

a2

(1 )

где a - параметр масштаба.

Оценку параметра распределения a можно получить, используя метод максимального правдоподобия (МП) (2):

•=Б

(2 )

где X j - значение элемента выборки, п -размер выборки.

Для рассматриваемой выборки значение а составляет 0.3505.

Статистические параметры выборки, подлежащее оцениванию, следующие: среднее значение, медиана, дисперсия, коэффициент вариации, коэффициент Лекси-са и коэффициент асимметрии.

В работе приводится оценка параметров выборки с помощью встроенных функций MATLAB [5], таких как: mean(), median(), var(), std(), skewness(). А также по известным соотношениям [2], используя полученную оценку параметра распределения по методу МП а.

В таблице 1 представлены значения статистических параметров, полученные относительно оценки а, а также полученные с помощью встроенных инструментов MATLAB.

Таблица 1. Значения статистических параметров выборки, полученные с помощью внутренних функций MATLAB, а также их расчёт с помощью полученной оценки д = 0.3505.

Статистические параметры выборки	Расчетные значения, полученные с помощью встроенных функций MATLAB	Расчетные значения, полученные с помощью оценки д
Среднее значение	0.4440	0.4392
Медиана	0.4229	0.4126
Дисперсия	0.0486	0.0527
Коэффициент вариации	0.4964	0.5227
Коэффициент Лексиса	0.1094	0.1200
Коэффициент асимметрии	0.5279	0.6311

Как можно видеть из таблицы 1, полученные двумя способами значения статистических параметров выборки оказались весьма схожими.

Анализ адекватности модели входных данных

В предыдущем разделе было сделано предположение о том, что рассматриваемая выборка данных имеет Рэлеевское распределение, а также по методу МП произведена оценка параметра распределения = 0.3505.

Для наглядной демонстрации того, насколько выбранная статистическая модель (Рэлеевское распределение с параметром д = 0.3505) близка к распределению экспериментальной выборки – на рисунке 2 представлена на одних осях теоретическая ФПВ случайной величины (СВ) и гистограмма для имеющейся выборки.

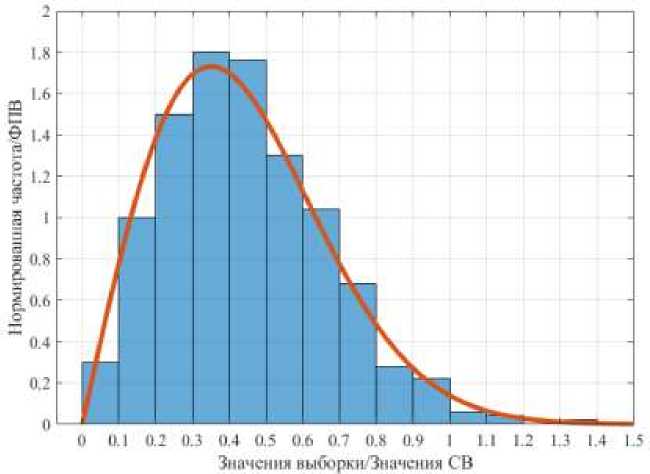
Рис. 2. ФПВ для распределения Рэлея, с также гистограмма экспериментальной выборки

Для проверки адекватности выбранной модели в качестве критерия согласия взят критерий хи-квадрат [3]. Данный критерий часто применяется на практике для сравнения эмпирического распределения с теоретическим.

Чтобы использовать критерий, необходимо знать зависимость распределения частот от двух сопоставляемых переменных. Для этого имеется гистограмма эмпириче- ских данных и аналитический вид ФПВ распределения Рэлея (рис. 2).

Уровень значимости альфа, при котором гипотеза о данном типе распределения не отвергается, принят равным а = 0.01.

Исходя из имеющихся данных, эмпирическое значение критерия составит: / 2мп = 0.151. Критическое значение при заданном уровне значимости / 2_р = 4.107.

Таким образом, / 2_р > / 2_мп . Это означает, что гипотеза о правильном выборе статистической модели не отвергается.

Алгоритм формирования случайных чисел по закону Рэлея.

Реализация алгоритма выполнена с помощью метода обратных функций. На рисунке 3 представлена блок-схема алгоритма, реализующего метод обратной функции для Релеевского распределения [4].

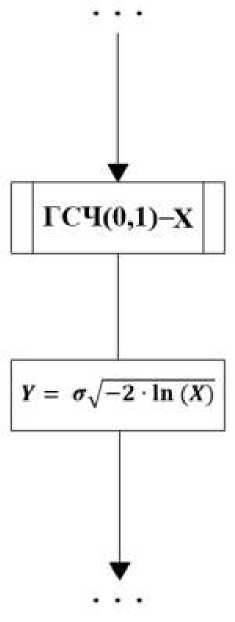
Рис. 3. Блок-схема алгоритма, реализующего метод обратной функции для Рэлеевского распределения

В основе данного алгоритма должен лежать генератор случайных чисел (ГСЧ), распределённых по равномерному закону от 0 до 1. В качестве такого ГСЧ будет использоваться линейный конгруэнтный алгоритм [4] с параметрами: a=26125; c=1; m=224; x(1)=220.

Далее необходимо получить функцию, обратную функции Рэлеевского распределения вероятностей, такая функция имеет следующий вид (3):

Y = ц^-21п (Г) (3

)

где X - вектор значений, полученных с помощью описанного ГСЧ. Величина Y в этом случае распределена по закону Рэлея с заданным параметром (д = 0.3505).

Описанный алгоритм реализован в программной среде MATLAB. В качестве демонстрации результата работы алгоритма на рисунке 4 представлена гистограмма выборки сформированных чисел объемом n=500, и наложенная кривая теоретической ФПВ при д = 0.3505.

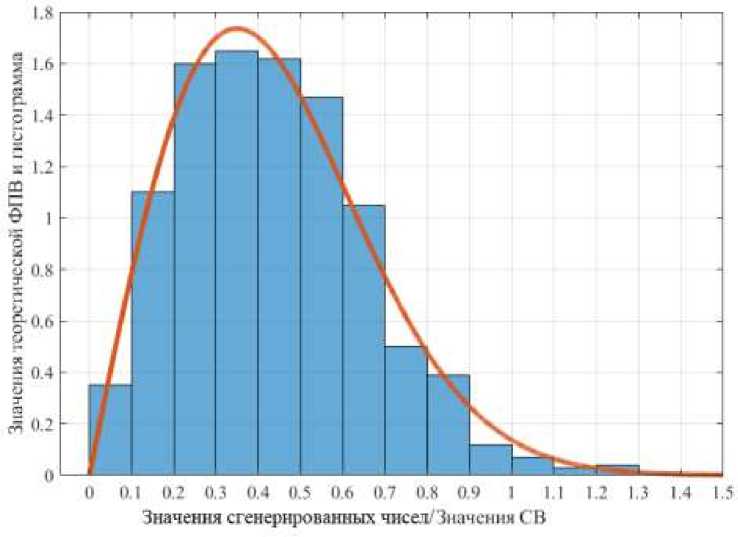
Рис. 4. Гистограмма полученной последовательности чисел и вид теоретической ФПВ

Заключение

В работе, по выборке экспериментальных данных, было сделано предположение о виде распределения (распределение Рэлея), произведён расчёт основных статистических параметров выборки с использованием инструментов программной среды MATLAB, а также расчет с помощью оценки по методу МП параметра распределения а = 0.3505. Результаты расчетов оказались схожими.

Для оценки адекватности модели использовался критерий хи-квадрат, который подтвердил корректность выбранной статистической модели (по уровню значимости а = 0.01). Метод обратных функций был успешно применен для генерации случайных чисел по закону Рэлея, что позволило синтезировать модель данных, соответствующую эмпирическим наблюдениям.

Результаты работы подтверждают, что использование программного пакета MATLAB является эффективным инструментом для статистического анализа и моделирования данных для сложных РТС. Предложенная методика может быть полезна при разработке и анализе статистических моделей в различных областях науки и техники, где требуется точная оценка и моделирование случайных процессов и величин.