Статистический метод анализа электрокардиосигналов в задаче обнаружения аритмий

Целью данной работы является создание, экспериментальное исследование и, соответственно, реализация алгоритма определения и различения различных видов аритмий с помощью использования статистических методов анализа и автоматизированных средств обработки электрокардиосигнала (ЭКС). Актуальность данной задачи обусловлена высокой смертностью из-за сердечно-сосудистых заболеваний и увеличением мощности современных вычислительных систем, позволяющих автоматизировать определение отклонений от нормального сердечного ритма (НСР).

В данной работе были использованы реализации ЭКС таких аритмий, как бигеминия, тригеминия и пароксизмальная наджелудочковая тахикардия (ПНТ), а также сигналы с НСР [1]. Была решена задача по созданию алгоритма, позволяющего определять наличие вышеуказанных аритмий и различать их между собой. Для достижения этой цели были использованы результаты работы [2]. А именно был использован коэффициент K , предложенный в качестве критерия выявления аритмии:

E Ui к = i=f*+1   ,                                             (1)

f rp

E U i i = 0

где знаменатель представляет из себя сумму гармоник низкочастотной (НЧ) части амплитудного спектра ЭКС, а числитель – сумму гармоник высокочастотной (ВЧ) части спектра. А f _rp является граничной частотой, разделяющей НЧ и ВЧ части.

Помимо этого были использованы плотности распределения вероятностей данного коэффициента для исследованных сигналов аритмий и «нормы». Но надо отметить, что результаты работы [2] были дополнены и подкорректированы. Во-первых, в связи с оценкой качества сигналов было изменено их количество для каждой аритмии и «нормы». Во-вторых, была рассмотрена еще одна аритмия – пароксизмальная наджелудочковая тахикардия. И наконец, в-третьих, было найдено другое оптимальное значение граничной частоты: f _rp = 13 Гц. Все это привело к изменению плотностей распределения вероятностей коэффициента K для исследованных ЭКС аритмий и «нормы» (рис. 1) и уточнению пороговых значений.

На этом рисунке, где цифрой 4 обозначена плотность распределения вероятностей величины K для тригеминии, цифрой 3 – для ПНТ, цифрой 2 – для бигеминии, цифрой 1 – для «нормы», можно наглядно увидеть пороги принятия решения: они определяются в тех местах, где пересекаются соседние плотности распределения вероятностей. Таким образом, получаем три пороговых значения: K ₁ – между «нормой» и бигеминией, K ₂ – между бигеминией и тахикардией, K ₃ – между та

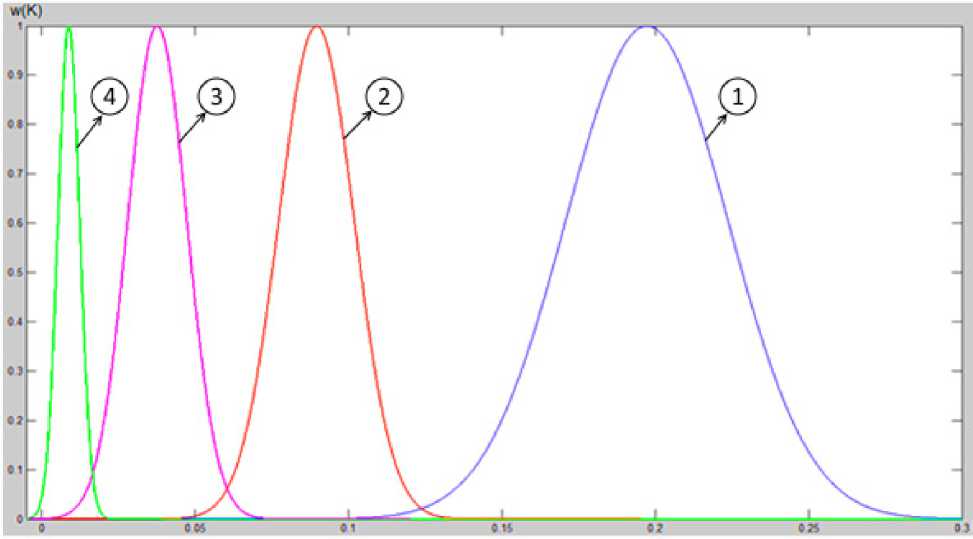
Рис. 1. Плотности распределения вероятностей случайной величины K

Рис. 2. Интервалы аритмий и нормы

Таблица 1

Пороги принятия решения

K1 K2 K3 0,1239 0,0606 0,0167 хикардией и тригеминией. Численные значения данных порогов представлены в табл. 1.

На рис. 2 покажем схематичное изображение порогов для облегчения понимания работы алгоритма, который будет представлен далее.

На основе имеющихся результатов был разработан алгоритм, который позволяет обнаруживать наличие аритмий и различать их между собой. Предложенный алгоритм состоит из следующих пунктов:

• •    Съем ЭКС.

• •    Нахождение с помощью БПФ амплитудного спектра 9-ти полных кардиоциклов снятого ЭКС.

• •    Вычисление для конкретного человека (сигнала) коэффициента K _чел с помощью формулы (1).

• •    Сравнение K _чел с порогами приведенными в табл. 1.

• •    Вынесение предварительного заключения.

Представим описанный алгоритм в форме блок-схемы (рис. 3) с учетом следующих обозначений:

Out – предварительное заключение (выходная величина); S ₀, S ₁, S ₂, S ₃ – «норма», бигеминия, тахикардия и тригеминия соответственно.

Далее было проведено экспериментальное исследование точности разработанного алгоритма. Для этого была определена вероятность ошибки, возникающей при определении «нормы» и каждой аритмии. При этом вероятностью ошибки, возникающей при определении «нормы» или же конкретной аритмии, будет являться так называемая вероятность «пропуска сигнала», так как с позиции конкретной аритмии выдвижение при ее наличии другого предварительного заключения (например, при наличии тахикардии, выдвижение заключения – бигеминия) будет считаться «пропуском аритмии». Термин «пропуск сигнала» часто используется в математической статистике и применительно к данной работе вероятность данного «пропуска» будет определяться по следующей формуле:

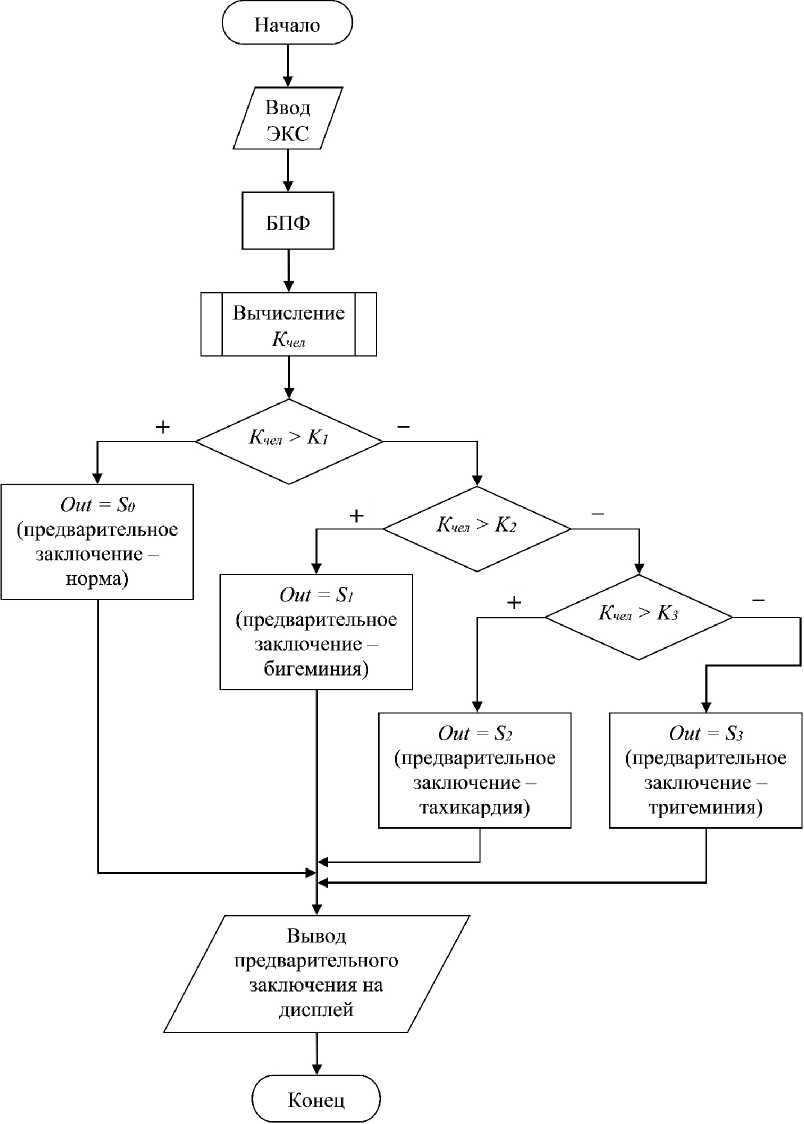
Рис. 3. Блок схема алгоритма обнаружения и различения аритмий

K i + 1                     K i + 3 0 i

Р ош.i =    J w ( K I S i ) dK + J w ( K I S i ) dK ,       (2)

Ki+i -3o i                    Ki где po0 i — вероятность ошибки, возникающей при определении нормы (i = 0), бигеминии (i = 1), тахикардии (i = 2) или тригеминии (i = 3); w(K | Si) -плотность распределения вероятностей коэффициента K для приведенных аритмий или нормы (зависит от индекса i); Ki – пороги, приведенные в табл. 1; стi - СКО соответствующих плотностей распределения вероятностей.

Формула (2) применима для нахождения вероятности ошибки при определении бигеминии ( i = 1) и тахикардии ( i = 2), а для тригеминии ( i = 3) и нормы ( i = 0) отсутствует первая или вторая составляющая формулы соответственно. То есть для тригеминии формула преобразуется в следующий вид:

Таблица 2

Вероятности ошибок, возникающих при определении нормы, бигеминии, тахикардии и тригеминии

p ош.0 , %	p ош.1 , %	p ош.2 , %	p ош.3 , %
0,2693	1,184	2,352	1,407

Таблица 3

Экспериментальные значения вероятностей принятия ошибочного решения

p ош.эксп.0 , %	p ош.эксп.1 , %	p ош.эксп.2 , %	p ош.эксп.3 , %
0	2,083	4,167	2,174

K 3 + 3 а з

Р ош.3 = J w ( K I ^S 3 ) dK ,                            (3)

K ₃

Для нормы:

K 1

Р ош.0 = J w ( K I ^S 0 ) dK ,                             (4)

K 1 - 3 0 1

Интегралы в формулах фактически представляют из себя площади под конкретными кривыми (рис. 1), зависящими от индекса i и находящимися в указанных пределах, отнесенные к общей площади тех же кривых плотностей распределения вероятностей коэффициента K . Необходимость делить на общую площадь возникает из-за того, что мы ранее получили нормированные кривые плотностей распределения вероятностей. Ведь как известно из теории вероятностей площадь под данными кривыми должна равняться единице, а деление на общую площадь как раз обеспечивает это условие.

С учетом вышесказанного и применением средств Matlab были р а ссчи т аны соответствующие вероятности (табл. 2):

Как видно из этих расчетов, наибольшая ошибка возникает при определении тахикардии. То есть вероятность того, что рассчитанный для конкретного человека коэффициент K попадет за пределы нужного интервала, получается самым высоким для пароксизмальной наджелудочковой тахикар-диии ( p _ош. ₂ = 2,352 %).

В нашей работе использовались 49 реализаций ЭКС «нормы» и 46-48 сигналов остальных аритмий. Сигналы были взяты из базы данных ресурса

PhysioNet [3]. В экспериментальной части исследования согласно алгоритму для каждого из этих сигналов строился амплитудный спектр, с помощью формулы (1) вычислялся коэффициент K , и проверялось попадание в заданный интервал найденного коэффициента. Далее рассчитывалась вероятность принятия ошибочного решения по результатам экспериментальных исследований как отношение неверно определенных случаев к общему числу случаев. Например, для бигеминии это вероятность составила:

Р ош.эксп.1 = ^8 = О,⁰²⁰⁸³ = ^2,083 %.

Таким же образом были найдены вероятности ошибочного принятия решения для остальных аритмий и «нормы». Результаты приведены в табл. 3.

Из сравнения табл. 2 и 3 видно, что вероятность принятия ошибочного решения для каждой аритмии получилась больше для экспериментальных значений, а для «нормы» наблюдается обратная ситуация. Это можно объяснить относительно малым количеством обработанных ЭКС для каждого вида сигнала.

Таким образом, была решена задача обнаружения и различения определенных видов аритмий. Исходя из полученных результатов можно сделать вывод о необходимости расширения базы сигналов с целью уточнения полученных пороговых значений, что, в свою очередь, должно привести к повышению точности обнаружения исследованных аритмий. Так же в качестве дальнейшего развития данной работы предлагается расширение списка различных видов аритмий.