Статистический подход к оптимизации сил крепежей при сборке авиационных конструкций

Одним из основных способов сборки деталей в авиастроении является крепежное соединение. Отдельные детали закрепляются на сборочном стенде и соединяются с помощью установки крепежей в заранее просверленные отверстия. Крепежи прижимают детали друг к другу и сводят зазор между соединяемыми деталями. Поскольку эта операция является достаточно времязатратной, оптимизация этого процесса относительно количества, расположения и типа используемых крепежей может значительно снизить затраты на сборочный процесс. Самым удобным на данный момент подходом к оптимизации сборочных процессов является математическое моделирование, поэтому данная статья рассматривает существующие методы моделирования сборочного процесса с использованием крепежей и предлагает метод анализа и оптимизации процесса крепежного соединения деталей применительно к авиастроительной области.

Математическое моделирование позволяет снизить затраты на проверку строгих требований к качеству сборки и определение наиболее оптимальных технологий сборки. Однако, для получения надежных результатов необходимо проводить моделирование с учетом специфики сборки конструкций в авиастроении.

Одной из особенностей процесса сборки в авиастроении является то, что собираемые детали представляют собой многокомпонентные и гибкие конструкции. Процессы сборки состоят из нескольких этапов, и они в большой степени подвержены вариациям сборки, возникающим из-за отклонений при изготовлении деталей и в процессе позиционирования и скрепления деталей. Для учета этих отклонений используется так называемое моделирование и анализ вариаций сборки.

На качество в процессах сборки самолетов влияют различные факторы, включая вариации формы деталей и высокую гибкость отдельных компонентов [1]. В области вариационного моделирования были разработаны специализированные методы моделирования сборочных процессов, учитывающие как отклонения отдельных деталей, так и вариаций самого сборочного процесса. Традиционный метод Монте-Карло (Direct Monte-Karlo, DMC) [2] основан на том, что для большого набора случайных отклонений проводят моделирование процесса сборки с помощью конечно-элементного анализа. Данный подход достаточно универсален [3], однако, для сложных конструкций этот метод становится чрезвычайно время затратным и не позволяет с достаточной точностью проводить оптимизацию отдельных аспектов сборочного про- цесса. Другая группа методов, основанная на методе коэффициентов влияния (Method of Influence Coefficients, MIC) [4], направленном на сокращение времени вычислений путем линеаризации задачи контакта. Это ускоряет вычисления, но снижает точность моделирования контактного взаимодействия [5]. В [6] предложена модификация МКЭ на основе редуцирования матрицы жёсткости и сведения контактной задачи к задаче квадратичного программирования. Использование этого подхода к моделированию сборочного процесса в авиастроении позволяет получить точное решение относительно перемещения деформируемых деталей в процессе сборки. Дополнительно, для данного подхода разработаны специальные численные методы [7], позволяющие существенно снизить время расчётов.

Особенности сборки деформируемых деталей с помощью крепежей

Отклонения формы и размера собираемых деталей и случайные отклонения позиционирования деталей приводят к тому, что до установки крепежных элементов между деталями образуется ненулевой начальный зазор. Поскольку источник этих зазоров – это случайные отклонения, то и результирующие зазоры имеют случайный характер.

Установка крепежей призвана свести эти зазоры до минимума, учитывая возможную вариативность этих зазоров. Результирующие зазоры между деталями, остающееся после установке крепежей, могут снизить качество сборки и повлиять на усталостную долговечность самолета. На практике на результирующие зазоры между деталями накладывают где х - это вектор перемещений деталей в зоне стыка, К - редуцированная матрица жесткости, f - вектор, содержащий силы от крепежных элементов, gres - результирующий зазор между деталями после установки крепежей, [5] у - вектор, определяющий ограничения на зазор в местах установки крепежей: это вектор равен 5 в тех узлах, где установлены крепежи, и равен +^ во всех других узлах.

ограничения в виде допуска: эти зазоры необходимо свести до какого-то небольшого заданного значения.

Для того, чтобы свести зазоры, установленные крепежные элементы прикладывают заданную сжимающую силу, которая зависит от типа и технологии используемого крепежа. В ответ на эту силу и на возникающее контактное взаимодействие в деталях появляются ответные сборочные силы и, соответственно, сборочные напряжения. Большие сборочные напряжения являются рискованными, так как могут привести к образованию трещин и снижению прочности материала, что критично для безопасности использования самолета в полете. По этой причине, при установке крепежей требуется приложить минимальную сжимающую силу. Вместе с тем, эта сила должна гарантировать сведение зазора между деталями.

Таким образом, в процессе разработки сборочного процесса с крепежным соединением возникает следующая задача: необходимо оценить минимальные силы, которые нужно приложить в крепежных элементах для того, чтобы результирующие зазоры между соединяемыми деталями не превышали заданного допуска.

Оценка сил в крепежных элементах

Подход, предложенный в [6], позволяет сформулировать контактную задачу, описывающую процесс соединения деформируемых деталей с ограничением на зазор в местах установки крепежей, в виде решения задачи следующего вида [8]:

min (—х^тК х — f^Tx ), 0< g™^s <[%\2         ^J   )

Результирующий зазор вычисляется как g^res = g^mit — А^тх, где g^mit - начальный зазор между деталями, А - матрица, определяющая контактные пары узлов. Решение задачи (1) в двойственной постановке позволяет через использование множителей Лагранжа получить значения сил f в крепежах, которые гарантируют сведение зазора в местах установки крепежей до 5 мм. На рисунке 1 приведена соответствующая схема моделирования соединения деталей.

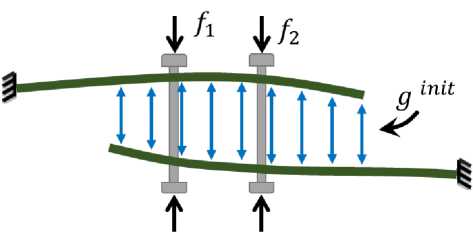
(а) до установки крепежей

Рис. 1. Схематичное предствление соединения деталей

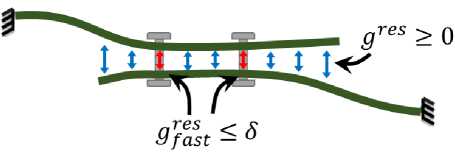
(б) после установки крепежей

В данной постановке случайные отклонения задаются в виде начального зазора. Учитывая случайность результирующих зазоров, для нахождения требуемых сил предлагается использовать подход Монте-Карло, то есть проводить серию расчётов для большого числа сгенерированных начальных зазоров. Методы моделирования начальных зазоров на основе модели случайного поля предложены в [9].

В результате серийных расчётов для каждого i-ого крепежа получается итоговая выборка значений сил F¹ = {/Д)_к_₁ ,, где ^ — число расчётов (соответствует числу сгенерированных начальных зазоров). Для того, чтобы оценить оптимальные силы, предлагается использовать статистические оценки характеристик этой выборки – можно рассмотреть среднее, разные квантили и максимальное значение получившегося распределения.

От выбора конкретной статистической оценки зависит величина получаемых сил и, соответственно, качество соединения деталей. Для сравнения эффективности и подбора нужной оценки предлагается проводить тестирование получаемых наборов сил. В качестве оценки качества соединения деталей можно оценивать статистическую кривую

(функции распределения) для результирующих зазоров, получаемых при использовании тестируемого набора сил. По получаемым статистическим кривым и заданным требованиям допуска на результирующий зазор выбирается наиболее оптимальная статистическая оценка выборки, соответственно, оптимальный набор значений сил в крепежах. В следуем разделе данной стати применение предлагаемой методики иллюстрируется на конкретном практическом примере.

Применение предложенного метода для процесса сборки

Для иллюстрации эффективности предлагаемой методики рассматривается одна стадия процесса сборки самолета: процесс присоединения к крылу укрепляющих накладок. На Рисунке 2 приведены общий вид модели и конкретная зона стыка с рассматриваемой расстановкой крепежей. Крепежи в этом процесса разделены на 5 групп по конкретным типам (на рисунке отличаются цветами), каждая группа крепежей характеризуется своей сжимающей силой f\..., f⁵. Необходимо оценить требуемые силы для каждой группы крепежей, чтобы снизить результирующий зазор до Л = 0.2 мм с вероятностью Р = 95%.

(а) общий вид

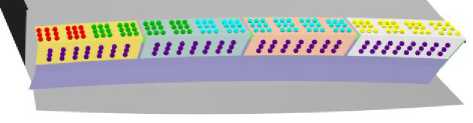
(б) расстановка крепежей

Рис. 2. Модель исследуемого соединения

Для рассматриваемого процесса сборки на основе модели случайного поля была сгенерирована выборка случайных начальных за- зоров (пример такого зазора приведен на рисунке 3(а)). Для каждого начального зазора проводилось решения задачи (1). На рисун- ке 3(б) приведен пример результирующего зазора, соответствующего представленному начального зазору. Из решения задач также были получены силы, сводящие результирующий зазор до 3 = 0.01 мм в местах установ- ки крепежей. Поскольку с рассматриваемой постановке крепежи разделены на группы, внутри каждой группы выбиралось максимальное значений силы.

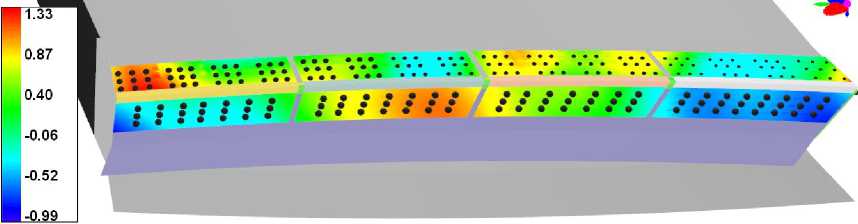
(а) Начальный зазор до установки крепежей и контактного взаимодействия

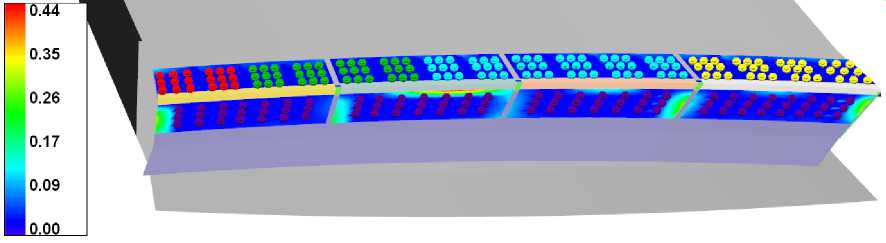
(б) Результирующий зазор после установки крепежей

Рис. 3. Моделирование процесса присоединения накладок к крылу

По итогам расчётов для N = 200 начальных зазоров, получились выборки F¹,., F⁵ для каждой группы сил, где F^l = {/i, ■ ■■,/ }• В качестве статистических оценок для этого примера будут рассматриваться среднее значение, 95-й квантиль и максимальное значение выборки. Пример полученных выборок для двух групп приведены на Рисунке 4, где отображены гистограммы для выборок, а также оценки (среднее, 95-й квантиль и максимум). Полученные оценки для всех групп крепежей приведены в таблице 1.

Для каждой оценки проводилось тестирование полученного набора сил: проводился анализ сборочного процесса на втором наборе сгенерированных начальных зазоров, по итогам которого строились распределения значений результирующего зазора (статистические кривые) 5(x) = Prob {gres < x}, x G R. Полученные кривые приведены на рисунке 5.

По полученным данным видно, что под требование уменьшить результирующий зазор до △ = 0.2 мм с вероятностью P = 95% подходят два набора сил (оценка с помощью 95ого квантиля и по максимальным значениям), а оценка с помощью средних значений не дает нужного качества соединения деталей. Соответственно, если выбирать минимальные силы из исследованных, то подходящим набором будут значения, оцененные с помощью 95-ого квантиля. В дальнейшем для уточнения оценок можно провести дополнительные исследования и найти также минимальный уровень квантиля, который будет подходить заданным требованиям.

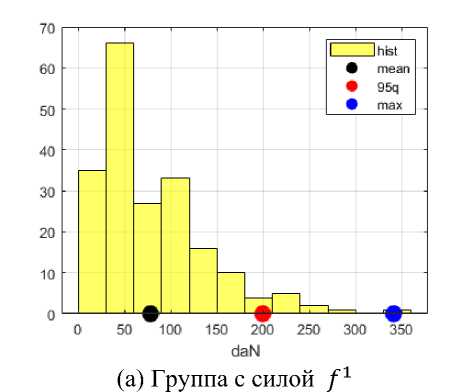
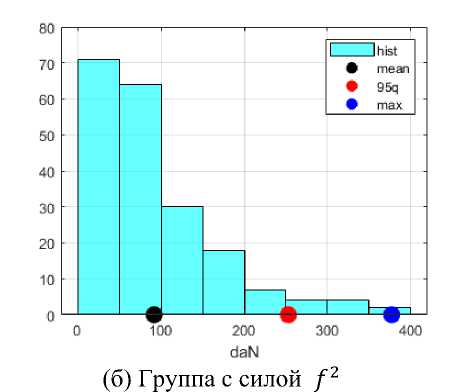
Рис. 4. Примеры полученных распределений для сил в крепежах

Таблица 1. Статистические характеристики для оценки полученных сил в крепежах

Тип крепежа	Цвет отображения			Оценка силы, даН
				Средне значение	95-й квантиль	Максимальное значение
f1		11		78	199	341
f2		2в		92	253	377
f3		22		99	274	515
f4		33		94	238	308
f5		44		150	290	413

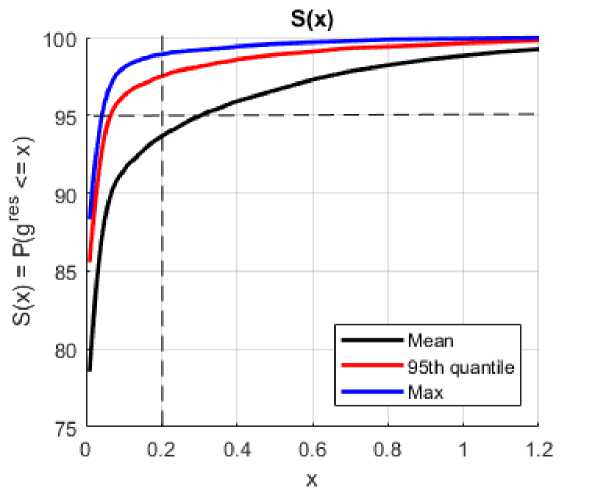
Рис. 5. Полученные функции распределения результирующего зазора (статистические кривые) для разных оценок сил в крепежах

Заключение

В ходе исследования была разработана методика оптимизации процесса сборки деформируемых деталей с использованием крепежных элементов, позволяющая решить проблемы, связанные с вариативностью зазоров между деталями. Применение математического моделирования и метода Монте-Карло дало возможность оценить минимальные силы, необходимые для обеспечения требуемого качества соединения. Результаты практического примера продемонстрировали, что использо- вание статистических оценок, таких как 95-й адаптирован для применения в различных об- квантиль и максимальные значения, является наиболее эффективным подходом для достижения заданных требований к результирующим зазорам. Данный метод может быть ластях машиностроения и авиастроения, спо собствуя улучшению надежности и безопас ности сборочных процессов.