Статистическое моделирование формирования макроструктуры порошковых материалов при одностороннем прессовании

Как известно, существуют целые направления классических исследований, посвященных математическому моделированию процесса прессования порошков [1-10]. В настоящее время с развитием информационных технологий характеристики макроструктуры порошковой среды могут удовлетворительно оцениваться статистическим моделированием с использованием вероятностногеометрических систем моно- и полидисперсных частиц [11-15]. Как показывают работы в этом направлении, статистическое моделирование качественно отражает основные закономерности формирования макроструктуры порошковых материалов в технологических процессах прессования, спекания и напыления. Одной из актуальных задач данных подходов является изучение формирования кластеров макроструктуры при уплотнении, отражающих взаимосвязь элементов макроструктуры прессованных порошковых материалов и, безусловно, связанных с их свойствами переноса и прочности.

Цель работы: выявление  особенностей формирования неоднородной и  анизотропной макроструктуры порошковых материалов при одностороннем прессовании на основе статистического моделирования вероятностно-геометричес кой системой порошковой среды.

Статистическое моделирование формирования макроструктуры порошковых материалов при одностороннем прессовании. На неоднородность и анизотропию физико-механических свойств порошковых материалов существенно влияют технологические процессы прессования, при которых в микрообъеме всегда существует выделенное направление уплотнения макроструктуры порошковой среды [1-10]. Поэтому исследования неоднородности и анизотропии макроструктуры порошкового материала при уплотнении позволяют оценить и прогнозировать его свойства. Неоднородность и анизотропия макроструктуры порошкового материала при формовании в пресс-форме возникают в результате внешнего воздействия ее деталей – матрицы и пуансона.

В работе для исследования формирования макроструктуры порошковых материалов при одностороннем прессовании использована элементарная двумерная модель Монте-Карло сечения порошковой среды. Как отмечено выше, дело в том, что при уплотнении порошковой среды направление прессования является выделенным, что позволяет рассматривать двумерные сечения макроструктуры (рис. 1). Модель построена на основе статистического подхода, предложенного в работе [11], где в качестве количественных характеристик макроструктуры выбраны продольные, поперечные (к направлению прессования) координационные числа частиц и локальная пористость при каждом шаге прессования. Экспериментальное определение данных характеристик макроструктуры в процессе прессования представляется практически невозможным из-за сложности наблюдения за большим количеством частиц порошкового материала. Статистическое моделирование описывает коллективное поведение частиц порошкового материала, на основе которого можно качественно описать процесс уплотнения порошковых материалов при прессовании.

Начальное состояние прессуемого порошкового материала задается прямоугольной матрицей макроструктуры, которая случайным образом заполняется частицами порошка [11]. Следует отметить, что начальная пористость в двумерных моделях макроструктуры задается с учетом заполнения частицами сечения трехмерной порошковой засыпки. Состояние макроструктуры порошкового материала на определенном шаге прессования получается из предыдущего состояния переносом частиц крайнего столбца по горизонтали в ближайшую незаполненную ячейку; после переноса всех заполненных элементов крайний столбец удаляется. Таким образом, процессу одностороннего прессования порошкового материала соответствует последовательное сокращение одного крайнего столбца матрицы. Если все ячейки в строке окажутся заполненными (возникновение перколяции ), процесс прессования считается законченным [11].

Рис. 1. Фрагмент вероятностно-геометрической системы [11]; х – направление одностороннего прессования

В работе по данной модели Монте-Карло при каждом шаге прессования вычислялись распределения одномерных кластеров макроструктуры. Для модели разработаны программы на языках Pascal и Delphi, которые позволяют описать изменение макроструктуры в матрицах размером до 1000x1000 с усреднением по 10000 реализациям. Таким образом, для анализа макроструктуры при статистическом моделировании использован линейный метод: в качестве характеристики макроструктуры выбрано распределение ns одномерных кластеров по размерам s; используются координаты (столбцы и строки матрицы вероятностно-геометрической системы) с осью х вдоль направления прессования, начало координат – на границе прессования (рис. 1).

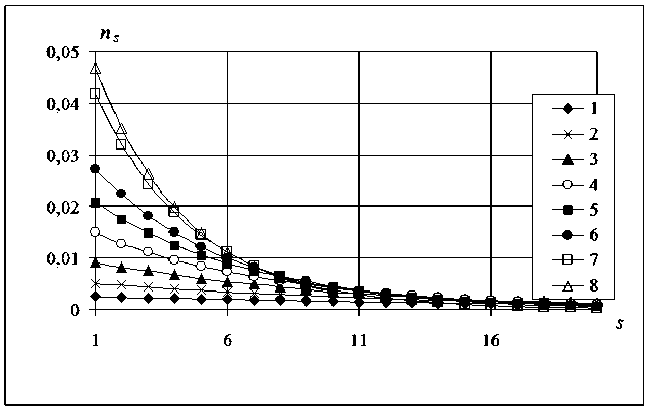
Обсуждение результатов. На рис. 2а показаны распределения кластеров n s в сечениях порошкового материала, перпендикулярных направлению прессования. Как видно из рисунка, при больших значениях х , когда плотность материала близка к начальной, распределение кластеров по размерам (график 7) близко к теоретическому (график 8), рассчитанному для равновесной одномерной цепи [16]; наблюдается преобладающее количество кластеров малого размера. С повышением плотности кластеры объединяются в более крупные, поэтому количество малых кластеров быстро сокращается (графики 6-3). Однако абсолютный рост количества крупных кластеров по сравнению с остальными кластерами незначителен (т.к. для образования крупного кластера требуется большое количество малых кластеров). С дальнейшим повышением плотности (при уменьшении х ) распределение кластеров по размерам становится практическим равномерным, общее количество кластеров значительно сокращается (график 1). Зависимость распределения n s от координаты вдоль направления прессования х указывает на неоднородность макроструктуры порошкового материала.

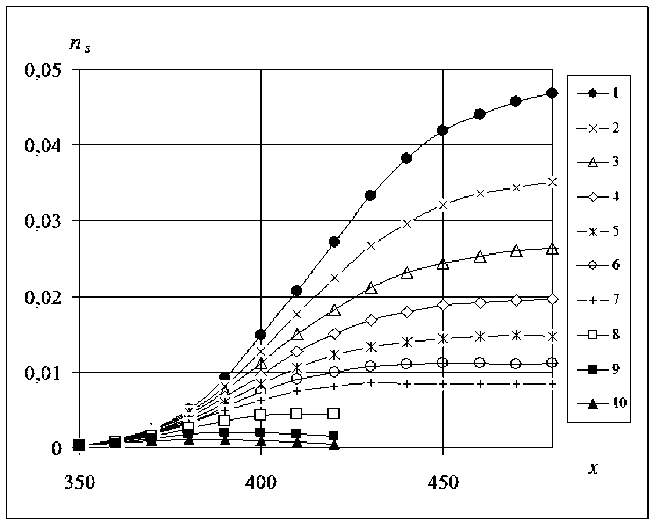
Для более полного исследования влияния стенки пуансона на неоднородность макроструктуры порошкового материала следует рассмотреть распределения n s кластеров поперечных сечений при различных размерах кластера s . Анализ поведения данной характеристики показывает, что в области с высокой плотностью количество кластеров практически одинаково (рис. 2б). При больших расстояниях х по направлению прессования, со снижением плотности наблюдается рост количества кластеров. Далее (примерно с х =380), количество крупных кластеров начинает незначительно снижаться (графики 9,10); распределение малых кластеров продолжает расти, хотя при увеличении размера кластера s скорость роста замедляется (графики 5-7). Вдали от области прессования , где плотность макроструктуры сохраняет своё начальное значение, характеристики n s стабилизируются для всех кластеров, что означает исчезновение неоднородности макроструктуры сечений порошкового материала. Анализ поведения данной характеристики n s в сечениях по направлению прессования, показывает, что количество кластеров убывает с ростом их размера s и является постоянным по сечениям.

а) в поперечных сечениях

• б) по размерам

  Рис. 2. Распределения одномерных кластеров: а) сечения х: 1-370; 2- 380; 3- 390; 4- 400; 5 -410; 6-420; 7- 450; 8 - одномерная цепь; б) размеры 1 - 7 - 5 =1,2,3,4,5,6,7; 8 - 5 =10; 9 - 5 =15; 10 - 5 =21; начальная плотность 0,75; матрица 300*1200; число реализаций модели 6000; шаг прессования 100

Как видно из графиков 8, 9, 10 на рис. 2б, количество крупных кластеров по сравнению с малыми кластерами является небольшим; однако их вклад в макроструктуру порошкового материала из-за большого объема является значительным. Поэтому необходимо подробнее рассмотреть изменение п₅ по сечениям вдоль направления прессования при больших значениях s. На рис. 3 приведены распределения крупных ( s> 25) одномерных кластеров поперечных сечений области уплотнения макроструктуры. Анализ данных распределений показывает, что изменение n 5 по поперечным сечениям происходит по качественно одинаковым закономерностям. Вдали от области уплотнения (справа на рис. 3)

количество кластеров крупных размеров близко к нулю; затем с уменьшением х и повышением плотности макроструктуры наблюдается возрастание п₅ . Далее, (в интервале от 370-380) распределения крупных кластеров достигают своего максимального значения, и далее наблюдается их устойчивое снижение. Это обусловлено формированием сверхкрупных кластеров, сопоставимых с размером сечения, вследствие снижения пористости материала и роста плотности макроструктуры. Таким образом, следует отметить наличие неоднородности макроструктуры порошковой среды при уплотнении в отношении одномерных кластеров сечений, перпендикулярных направлению прессования (рис . 3).

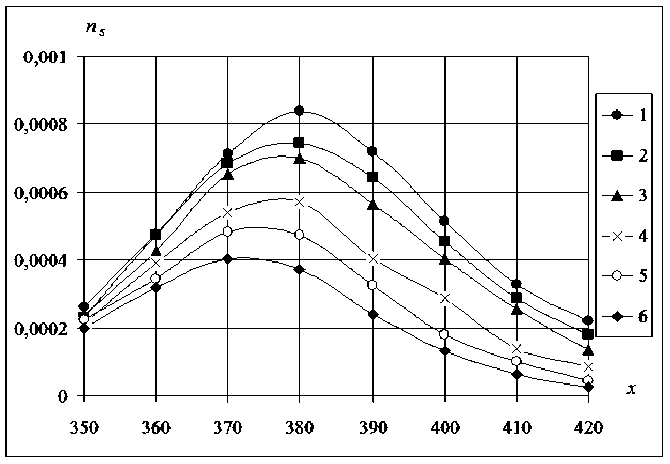
Рис. 3. Распределения крупных одномерных кластеров поперечных сечений в зависимости от размера: 1– s= 25 ; 2– s= 26; 3– s= 27; 4– s= 26; 5– s= 32; 6– s= 35; начальная плотность 0,75; матрица 300×1200; число реализаций модели 6000, шаг прессования 100

Для сравнения неоднородности по кластерам разных размеров более целесообразно рассматривать характеристику s ^ns- долю сечения занимаемых кластерами размера s (рис. 4). Данная характеристика также интерпретируется как вероятность того, что произвольно выбранная ячейка сечения будет принадлежать кластеру размера s [16]. Как и в случае распределения кластеров по сечениям (рис. 2б), при увеличении х наблюдается рост доли кластеров малого размера с дальнейшей стабилизацией при достижении области с начальной плотностью. При этом также наблюдается рост с последующим снижением доли крупных кластеров. Причём изменения исследуемой характеристики s ^ns при s=10–30 сопоставимы с изменениями при малых размерах кластера s (рис. 4). Наибольшее изменение имеет доля сечения, принадлежащая кластерам размера s =4, тогда как ранее для характеристики ns максимальный рост наблюдался у кластеров размера s =1 (рис. 2б). Рассмотренные характеристики дают детальное представление об изменении макроструктуры порошкового материала при уплотнении односторонним прессованием.

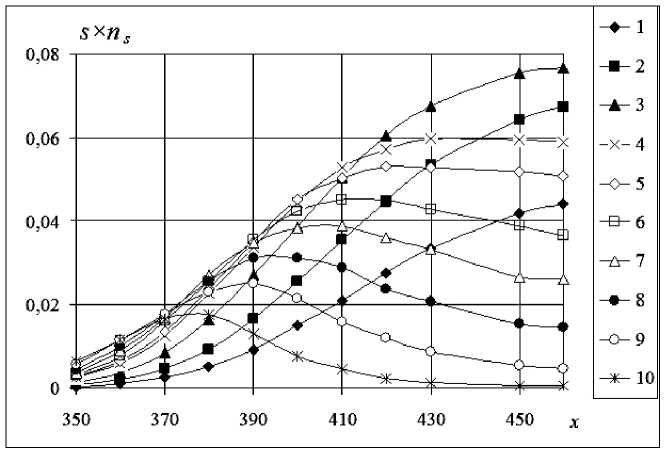
Рис. 4. Изменение доли поперечного сечения, занимаемой кластерами размера s : 1– s= 1; 2– s= 2; 3– s= 4; 4– s= 7; 5– s= 8; 6– s= 10; 7– s= 12; 8– s= 15; 9– s= 20; 10– s= 30; начальная плотность 0,75; матрица 300×1200; число реализаций модели 6000, шаг прессования 100

Выводы:

• 1.    На основе двумерной статистической модели сечения макроструктуры порошковой среды исследовано формирование неоднородной и анизотропной макроструктуры порошкового материала при одностороннем прессовании. Установлено, что с удалением от границы прессования распределение кластеров по размерам приближается к равновесной упаковке; наблюдается преобладающее количество кластеров малого размера. При этом распределения всех кластеров в поперечных сечениях стабилизируются, что означает исчезновение неоднородности макроструктуры сечений порошкового материала. При приближении к границе прессования распределения кластеров по размерам становятся практически одинаковыми и равномерными, общее число кластеров значительно сокращается. Установлено, что в сечениях по направлению прессования количество кластеров убывает с ростом их размера и является постоянным.

• 2.    Выявлено, что для крупных кластеров (при s >25) с приближением к границе прессования изменение распределения является немонотонным из-за механизма формирования сверхкрупных кластеров. С удалением от границы прессования наблюдается рост доли крупных кластеров с последующим снижением; наибольшее изменение имеет доля сечения, принадлежащая кластерам размера s = 4, тогда как для распределения максимальный рост фиксировано у кластеров размера s = 1.