Статистическое моделирование процесса потребления воды животными

Введение. Потребление воды животными на ферме является случайным, вероятностным процессом и характеризуется одновременным воздействием на систему автопоения большого числа животных. Практически невозможно создать типовой детерминированный график потребления воды животными на ферме. Поэтому для более точного описания этого процесса воспользуемся методом статистического моделирования и опишем его на основе статистического анализа графиков суточного потребления, полученного путем экспериментальных наблюдений.

Для получения суточных графиков водопо-требления необходимо проводить длительные, многолетние наблюдения, требующие затрат как времени, так и средств [1, 2].

Материалы и методы исследования. В связи с этим для сокращения длительности наблюдений нами предлагается использовать метод статистического моделирования с применением ЭВМ.

Процесс потребления воды животными можно отнести к системам массового обслуживания, поэтому для постановки задачи воспользуемся терминами этой теории.

Животные, находящиеся в животноводческом помещении и являющиеся основными потребителями воды, служат источниками заявок на обслуживание.

В соответствии с теорией массового обслуживания процесс автопоения представляет собой случайную последовательность заявок на обслуживание, формирующую входящий поток требований.

Входящий поток требований не является неизменным. Он зависит от времени года (осенне-зимний и весенне-летний периоды). В соответствии с положениями, изложенными P.M. Славиным в работе «Автоматизация процессов в животноводстве и птицеводстве» (1991 г.), поточные процессы можно описать методом ста- тистического моделирования. В этом случае основной характеристикой входящего потока является распределение интервала времени между поступлением заявок на обслуживание.

Процесс обслуживания КРС задается следующими параметрами: распределением времени обслуживания поступивших заявок, числом одновременно обслуживаемых заявок и количеством мест обслуживания поступивших заявок [3–6]. Заявки, которые были обслужены, образуют выходящий поток.

Оценка качества обслуживания животных производилась в соответствии со следующими показателями:

– распределение количества одновременно пьющих воду животных;

– распределение длительности потребления воды животными.

Результаты исследования и их обсуждение. При моделировании процесса потребления воды животными были приняты следующие их состояния: животное испытывает потребность в воде, животное частично утолило жажду, животное полностью утолило жажду.

В основу модели процесса потребления воды животными были положены следующие правила:

• 1.    Животное не может начать потребление воды из автопоилки раньше момента времени, относительно которого отсчитываются все последующие события.

• 2.    Животное, полностью использовавшее моделируемое время потребления воды, считается полностью обслуженным и покидает систему автопоения.

Моделирование позволяет описать процесс потребления воды животными из автопоилок, входящих в систему автопоения, при помощи математических зависимостей, полученных на основе экспериментальных данных [7, 8].

Входящий поток требований может быть представлен в виде функции x = x ( т ) , определяющей число заявок на обслуживание в течение промежутка времени (0, т ). Функция x ( т ) является случайной величиной для каждого значения времени т.

Входящий поток требований определяется при моделировании продолжительности промежутков времени между подходами животных к автопоилке и вероятности появления i, j заявки ( Рi, j ), обладающей следующими свойствами [8, 9]:

[ х₁ ] > 0 для всех i

Р [ х или х j ] = Р [ х ] + Р [ х j ]

Плотность распределения f(x) непрерывной случайной величины х процесса водопо-требления определим при помощи интегральной функции распределения [10, 11].

f ( x ) = lim ^{Р (} х х —^А х ' .  (2)

• V      Ах >01           Дх

Функции плотностей вероятностей моделировали в соответствии с нормальным и экс- поненциальным законами распределения, а также законом распределения Вейбулла [10, 12, 13].

Нормальный закон распределения:

ях) =

«г • ЯП

- ( х -ц )) 2 г ²    ,

где ц - математическое ожидание;

• г - среднеквадратическое отклонение;

Г - дисперсия случайной величины.

Экспоненциальный закон распределения:

'ее " ^{2 х}, х >  0,

0,     х<0 ,

f ^{( x} ) =

где х – случайная величина;

λ – параметр, являющийся постоянной ложительной величиной.

Закон распределения Вейбулла:

f^{( х)} =‘

k

1 f X к - 1       I х I

--I х I  -е^-^ е)   х>0

I I е , х V.

по-

0,                    х < 0, где k, λ – параметры;

x – случайная величина.

Закон распределения Вейбулла в отличие от экспоненциального характеризуется двумя параметрами k и λ, являющимися положитель- ными реальными числами. Параметр k характеризует форму кривой распределения, а λ – масштаб распределения случайной величины [14, 15].

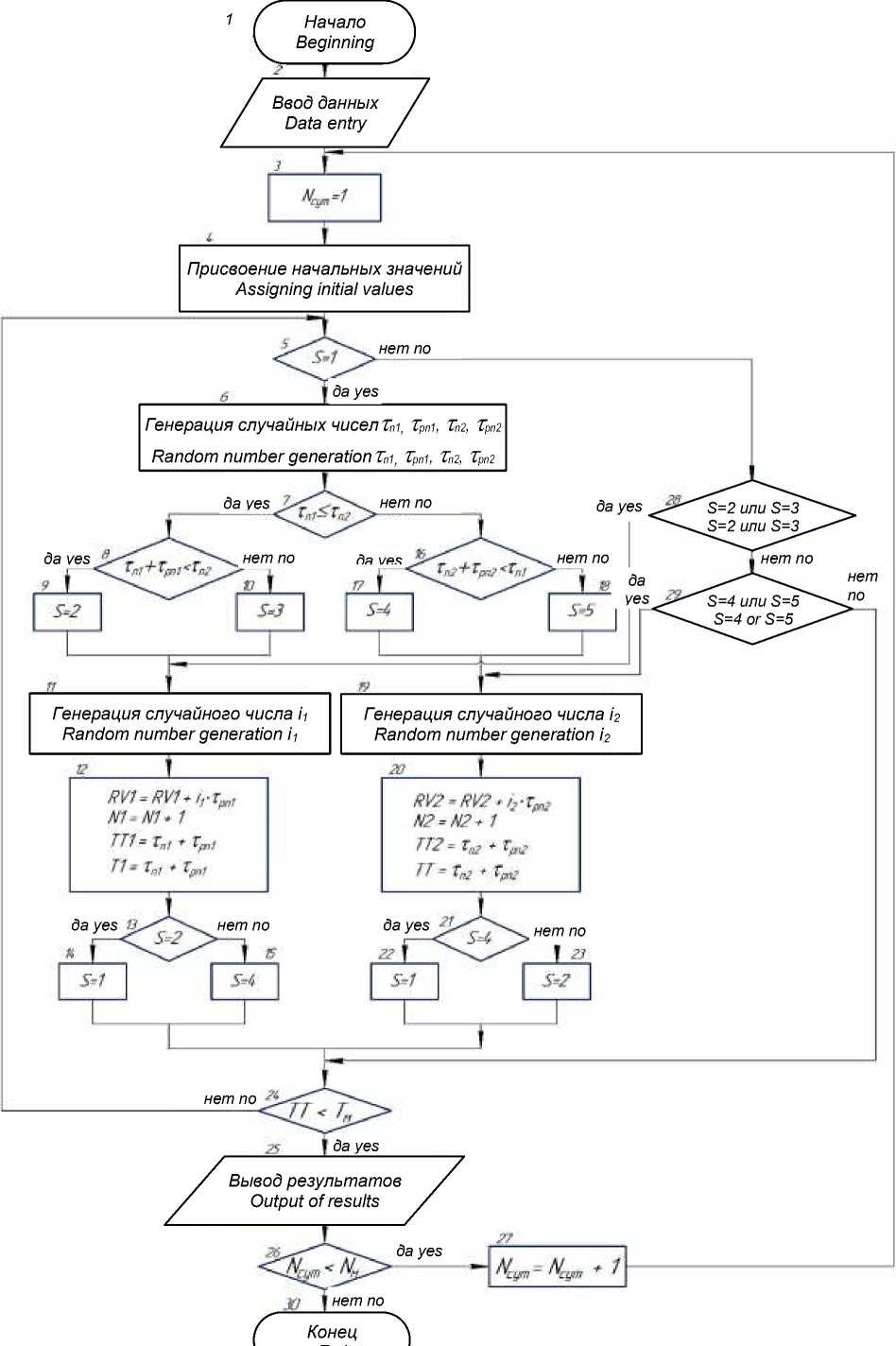
Для описания процесса поения коров составим алгоритм, моделирующий работу системы автопоения. Предлагаемый нами алгоритм включает в себя следующие основные блоки: блок ввода исходных данных для моделирования процесса потребления воды животными; блок присвоения переменным величинам исходных значений (присваивается нулевое значение текущему времени суток Т , числу подходов животных к поилке N i , значению расхода воды в системе автопоения RV i , времени начала обслуживания животных ТТ i ); блоки проверки состояния системы автопоения ( S ); блок генерации случайных чисел характеристик обслуживаемых животных: промежутка времени между подходами животных к автопоилке (т пі ); продолжительности разового потребления воды животным (т рпі ); интенсивности потребления воды одним животным ( i ); блоки проверки возникновения потребности в поении у животных (т пі ^ т п2 ); блоки вычисления характеристик обслуживания животных ( RV i , N i , ТТ i , текущего времени суток ТТ ); блоки, проверяющие достоверность события; блок печати результатов моделирования и останова машины [11].

Для разрабатываемой модели будем задаваться следующими исходными данными:

T м – продолжительность моделирования, час;

N сут – число моделируемых суток, сут.;

М – число обслуживаемых животных, гол.;

П – продуктивность животного, кг;

t в – температура воды в системе автопоения, ^оС;

t возд – температура воздуха в коровнике, ^оС;

т п - промежуток времени между подходами животных к автопоилке, с;

т рп - продолжительность разового потребления воды животным, с;

– интенсивность потребления воды одним животным, л/с;

ТТ – текущее время моделирования, с;

ТТ – моменты времени, в которые животное начинает или заканчивает обслуживаться, с;

N – число подходов животных к автопоилке, раз;

RV i - текущее значение расхода воды животными, л.

В процессе моделирования система автопоения может иметь следующие состояния: S = 1 - система автопоения свободна; S = 2 -первая корова пьет, очереди нет; S = 3 - первая корова пьет, вторая корова ожидает поения; S = 4 - вторая корова пьет, очереди нет; S = 5 -вторая корова пьет, первая корова ожидает поения.

Состояние системы автопоения при моделировании процесса потребления воды животными можно представить в виде следующего графа (рисунок 1).

На начальном этапе процесса моделирования задаются начальные условия, характеризующие процесс потребления воды животными, генерируются значения интенсивности подходов коров к автопоилкам, длительности поения и фиксируется текущее время моделирования.

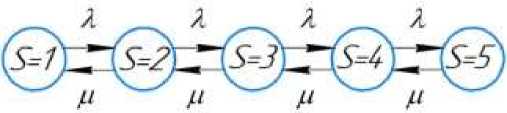
λ – интенсивность входящего потока; μ – интенсивность потока обслуживания Рисунок 1 – Граф состояния одноканальной системы массового обслуживания с ожиданием λ – intensity of incoming flow; μ – service flow intensity

Figure 1 – State graph of a single-channel system of mass service with waiting

Обслуживание животного считается оконченным по истечении моделируемой длительности водопотребления. После каждого изменения состояния системы автопоения определяется расход воды в ней и объём емкости, в которой осуществляется подогрев воды в зимнее время [11].

Длительность процесса моделирования регламентируется заданным числом реализаций или заданной длительностью моделирования.

Воздействие животных на систему автопоения осуществляется в виде однородных дискретных потоков. Животные, поступающие на обслуживание - поток подачи ф п (т) , а обслуженные животные - поток расхода ф р (т). Систему автопоения рассмотрим как регулирующую емкость, с сосредоточенной в ней регулирующей массой Ф(т), куда поступают потоки требований животных на обслуживание ф п (т) и выходят обслуженные заявки Ф р (т) :

^{Ф (т} ) = Ф п ( ^{Т ) -} Ф р ( ^Т ) . ⁽⁶⁾

При разработке модели процесса потребления воды животными будем считать, что поток заявок на обслуживание является стационарным (вероятность возникновения заявок на любом интервале времени от ті до т зависит только от величины этого интервала и не зависит от значения ті), ординарным (события возникают по одиночке, а вероятность одновременного возникновения двух и более заявок пренебрежимо мала) и отсутствует последействие (события возникают независимо друг от друга), то сделаем допущение, что входящий поток является пуассоновским. Количество коров, находящихся возле автопоилки, ограничено [14, 15].

Основными параметрами, характеризующими процесс потребления воды животными, являются максимальная и минимальная частота их подходов к автопоилкам. Интервал времени Т , через который происходит обслуживание животных, является основополагающей величиной.

Промежуток времени Т между случайными точками на временной оси является случайной величиной, которая подчиняется показательному закону распределения с параметром λ :

Ғ(т) = Р(Т < т) = 1 - е-х'т, (7)

f (т ) = ^F(L) = Х' e"‘", (8) ат где Ғ(т) - интегральная функция распределения интервала времени Т при т > 0;

f ( т ) - дифференциальная функция распределения интервала времени Т при т > 0.

Параметр λ является средним количеством заявок, поступающих на обслуживание в единицу времени. Он характеризует среднее число животных, потребляющих воду из автопоилок в единицу времени. Данный параметр позволяет рассчитать среднее значение промежутка времени между подходами животных Т в соответствии со статистическими характеристиками случайной величины Тср [9, 10, 14]:

Т ср = ¹ = ^m T = ^А т = DD .   (9)

л

где т _т - математическое ожидание случайной величины Т ;

D – дисперсия;

плотность поступления животных к автопоилке λ . В практических расчётах, при отсутствии экспериментальных данных, этот параметр определить практически невозможно. Поэтому возникает необходимость поиска параметра λ рас-

а - среднее квадратическое отклонение.

В соответствии с характеристиками случайной величины T ср закон промежутка времени между подходами животных к автопоилке Т можно представить в виде:

-т

Ғ( т ) = P(T < т ) = 1 - e ^ср .  (10)

Так как изменения случайной величины Т могут быть ограничены теми пределами, за которые она практически не выходит, то в практических расчетах этим можно пренебречь (правило трёх с ). Поэтому промежуток времени между подходами животных можно представить в данном виде:

т = m _T + к ■ А_т ,          (11)

четным путем.

Как известно, коровы потребляют воду несколько раз в течение суток. При этом наиболее активное потребление воды приходится на периоды кормления животных. На основании

этого можно сделать допущение, что как минимум одно из потреблений воды животными в течение суток будет приходиться на период кормления. В этом случае средняя плотность подходов животных к автопоилке λ будет равна:

Л = М , т рп

где к - кратность а .

С учётом выражения (9) выражение (11) можно представить в следующем виде:

^т = ^{( 1} + к) ■ а .           (12)

Следовательно, закон распределения случайной величины Т можно рассматривать в зависимости от кратности с_т , что позволяет определить минимальное и максимальное значения Т с вероятностью Р :

Т =Т -1пР(Т>Т А (13) min     ср                 min ,

где М – число обслуживаемых системой автопоения животных, гол.;

т рп - продолжительность разового потребления воды животными, с.

На основании этого получим новые выражения для определения граничных значений случайной величины частоты появления животных у автопоилок q :

M

q min             /1 ,     \ ;

^т рп • ^{( 1 + К)} M

q^max   т ■ lnP ■ (T >  T )

рп                  min

.

Это позволит определить режимные ха-

Т« = m ^mT + k ■ А .        (14)

max         т             т

Зная минимальное и максимальное зна-

чения случайной величины Т , определяем граничные значения случайной величины частоты

появления животных у автопоилок, которая ха-

рактеризует загрузку системы автопоения:

q min

T max

q max

T min

Основным управляющим параметром за-

рактеристики системы автопоения.

На основе предлагаемой статистической модели разработан алгоритм, моделирующий работу системы автопоения, блок-схема которого представлена на рисунке 2.

Генерация случайных чисел т пі (интервал времени между подходами 1-й коровы), т рпі (длительность разового потребления воды 1-й коровой), т п2 (интервал времени между подходами 2-й коровы), т рп2 (длительность разового потребления воды 2-й коровой) производится методом Монте-Карло в соответствии со следующими законами распределения: нормальным, экспоненциальным и Вейбулла [11].

грузки системы автопоения является средняя

да yes

Конец

S=2 или S=3

S=2 или S=3

S=4 или S=5

S=4 or S=5

нет no

Вывод результатов Output of results

”<>>

____[ да yes

26              да yes

<Япт*С>

Начало

Beginning

> 1

Ввод данных

Data entry да yes да yes

JU нет no нет no нет no да yes в

* f нет no нет no

Генерация случайного числа i 1 Random number generation i 1

Генерация случайного числа i 2 Random number generation i 2

нет no да yes L

_______________________I да yes

Генерация случайных чисел τ n1 , τ pn1 , τ n2 , τ pn2

Random number generation τ n1 , τ pn1 , τ n2 , τ pn2

RV2 -RV2 • Ь'^-

N2 = N2 + /

TT2 = T^ * ^

^^ * *^ti * ^pti

RV1=RV1 * trT^

N1- N1. 1

TT1= Tnf * T^)

^"1л Tn; * Tpn)

Присвоение начальных значений Assigning initial values

^cyn ^cym

%=J нет no yes

S-5

! * да нет no да yes

1               *PR? ^c*n!

нет no

-L1L

Рисунок 2 – Алгоритм, моделирующий работу системы автопоения Figure 2 – Algorithm simulating the operation of an automatic drinking system

Нормальный закон распределения:

3n х = Л аҮ(2R + 1) + m ,  (20)

V n    і = 1

где с - среднеквадратическое отклонение;

m – математическое ожидание;

R i – случайное число.

Экспоненциальный закон распределения:

х = —~ ln ( 1 ^- R ) ¹ Ц ,     ⁽²¹⁾

л где А, ц- параметры распределения.

Закон распределения Вейбулла:

(ln (-einRi)A х = e ^ Y ^,              (22)

где в, ү - параметры распределения.

Выводы. Анализ процесса потребления воды животными показал, что он носит случайный, вероятностный характер и может быть описан методом статистического моделирования.

В качестве основных исходных данных для статистического моделирования рабочего процесса системы автопоения необходимо использовать законы распределения интервалов времени между подходами животных к автопоилке, длительности и интенсивности потребления воды животными, определяемыми экспериментальным путём.

Предлагаемая модель позволяет определить суточный, часовой и секундный расходы воды, интенсивность и продолжительность потребления воды животными, при помощи которых можно обосновать конструктивные параметры системы автопоения и мощность нагревателя.

При сравнении результатов моделирования с экспериментальными данными, полученными на действующем объекте (коровнике на 200 голов), установлено, что их сходимость составляет 0,8–0,9. При этом наибольшая сходимость результатов наблюдается при почасовом моделировании процесса.