Статистическое оценивание эпидемии сифилиса 1990-2020

Сифилис – инфекционное заболевание. В России эта болезнь появилась в начале XVIII века, быстро распространилась по территории страны. В XIX веке количество заболевших в российских губерниях изменялось от 0.05 до 1.5% населения губернии. В период эпидемий заболеваемость достигала 50% [1]. Органы управления в разные времена применяли различные методы уменьшения заболеваемости населения [1, 2]. Тем не менее, за последние 200 лет на территории современной России было несколько вспышек заболеваемости. Последняя вспышка началась на рубеже XX и XXI веков в России и странах СНГ. Эпидемия возникла в результате экономического и политического распада СССР, последующего экономического кризиса, роста проституции, отменой мер по борьбе и профилактике инфекций [2]. В 1991 г. было зарегистрировано около 7 заболевших на 100 тыс. населения, а в 1997 г. – около 270. На начальном этапе эпидемии темпы роста составляли около 50% в год. На ликвидацию эпидемии ушло около 20 лет [3].

Сифилис – инфекционное заболевание, вызванное микроорганизмом бледная трепонема. Заболевание передается преимущественно половым путем при непосредственном контакте между людьми. Инфи- цирование может происходить и через переливание крови от больного к лицу восприимчивому к заболеванию, от зараженной матери к грудному ребенку через кормление молоком, к плоду через плаценту. Но эти варианты заражения составляют 2 - 3% от всех заболевших [4]. Таким образом, сифилис является эпидемическим заболеванием. Заболеть могут лица всех возрастов, включая младенцев. Болезнь может распространяться по территории на протяжении нескольких лет.

Данные о числе лиц, впервые заболевших сифилисом и их возрастной структуре, в целом по России публикуются в справочниках федеральной службы государственной статистики [3]. Наиболее полные данные представлены с 1990 по 2020 год. Данные по отдельным регионам публикуются в отчетах местных органов власти, научных публикациях различных авторов [5, 6]. Количество больных на 100 000 населения до 1990 г. держалось на уровне 5-15 человек. Начиная с 1990 г. происходит резкий рост числа больных.

Максимальное количество больных достигалось в западных регионах в 19951996 гг., а в восточных – в 2004-2005 гг. Максимальное количество больных на территории страны изменилось от 150 до 1200 на 100 000 населения. То есть заболе- ванию были подвержены в отдельных территориальных образованиях до 1.5% населения. В отсутствие эпидемии при стабильной медицинской поддержке заболеваемость не превышала 0.015% численности населения. В основную когорту больных входили граждане от 20 до 30 лет (около 70% от всех заболевших). На рисунке 1 отражена динамика заболеваемости сифилисом - число лиц, впервые обратившихся за медицинской поддержкой. Статистические данные отмечены символом «*». Если принять, что в 1990 г. «естественная» заболеваемость составляла 5-10 человек на 100 000 населения, то уменьшение заболеваемости до этого уровня могло произойти к 2025. То есть оценка длительности эпидемии - 25 лет.

Математические модели эпидемий появились в конце XIX в. В модели Кермака и Мак Кендрика учитываются инфицированные лица и восприимчивые к заболеванию. Предполагается, что передача ин- фекции происходит при непосредственном контакте инфицированных и восприимчивых лиц. Все восприимчивые постепенно заражаются, а инфицированные со временем выздоравливают и покидают когорту больных, смертность при контакте не учитывается. Эта модель лежит в основе современных моделей, учитывающих различные особенности протекания реальных эпидемий.

Анализ статистических данных по заболеваемости населения страны за последние 200 лет показывает, что среди населения все эти годы была небольшая когорта больных: в 19 веке около 1% населения [1], в конце XX века около 0.02% [6]. В дополнение к этому часть выздоровевших лиц (до 20% выздоровевших) заболевает повторно. То есть эта группа лиц остается восприимчивой к заболеванию [4]. С учетом этих факторов модель эпидемии сифилиса представлена системой двух дифференциальных уравнений

— — —aSI + у + sj3I, dt

— — aSI — BI, dt

где I - число инфицированных лиц, а S - восприимчивых. a , в , У и £ - параметры.

В уравнениях (1) a SI - скорость роста числа инфицированных лиц, PI - скорость «выздоровления», £ - доля выздоровевших, которые остаются восприимчивыми из-за возможности повторного заболевания. у - скорость пополнения группы восприимчивых за счет изменения численности населения, так как заболеванию подвержены все возрастные группы насе- ления. Поскольку число инфицированных значительно меньше, чем численность населения, то это скорость считается не зависящей от общей численности населения. На параметры £ и у накладываются ограничения:

0 <  £ <  1 , 0 <  у <<  S _o, где S_o - число восприимчивых лиц на момент начала эпидемии.

Системы уравнений (1) имеет единственную стационарную точку

S — в, I —--У—.

a      в(1 — £)

Собственные значения матицы Якоби правой части системы уравнений (1) в стационарной точке являются корнями уравнения

22 + a

в(1 - г)

2 + ay = 0.

Корни этого уравнения имеют отрицательную вещественную часть. В случае комплексно-сопряженных собственных значений возможны локальные колебания численности инфицированных лиц. Это означает, что после убыли инфицированных до стационарного состояния (2) возможен небольшой подъем числа заболевших с постоянным незначительным ростом их числа на протяжении нескольких лет.

Таким образом, модель (1) отражает факт постоянного наличия в обществе больных сифилисом с момента появления этого заболевания на территории страны [1]. В связи с этим одним из вариантов борьбы с эпидемиями сифилиса является мониторинг населения [5, 6] с предвари- тельной оценкой предрасположенности лиц к заболеванию [7].

В качестве начальных данных для функции I ( t ) бралось число больных на 100 000 населения в 1990 году. Система уравнений (1) решалась с применением численных алгоритмов решения нелинейных дифференциальных уравнений. Реализация осуществлялась в среде программирования математического пакета Matlab. На рисунке 1 отражены результаты численного решения – символом «*» отмечены статистические данные, расчетной зависимости соответствует пунктирная линия. Данные приведены для значений параметров a = 0.0018 , в = 0.25 , у = 6 , s = 0.1 .

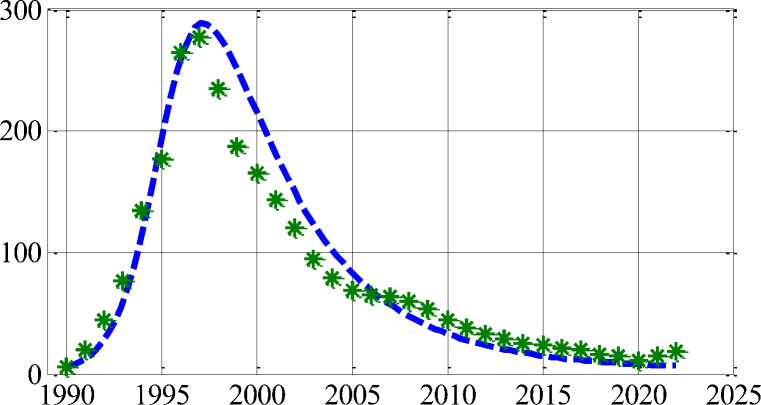
Год

Рис. 1. Динамика заболеваемости сифилисом

Аппроксимация аналогичных статистических данных для нескольких регионов России (Магнитогорск, Санкт-Петербург, Орловская обл., Ставропольский край, г. Астрахань, Иркутская обл. и др. регио- ны) и сопредельных с ней государств (Беларусь, Киргизия, Украина [5, 6]) позволила оценить диапазон изменения параметров, входящих в систему уравнений (1):

0.0005 < a < 0.0030, 0.0005 < a < 0.0030, 0.15 < в < 0.35, 2 < у < 20.  (3)

Распределение вероятностей «больных» «больных» и распределение вероятностей на пике заболеваемости численности времени наступления пика заболеваемости строились на основе имитационного моделирования и статистического метода псевдорандомизации [8]. Выбор параметров для системы уравнений (1) осуществлялся случайным образом из диапазонов (3). Результаты моделирования для 2 000 вариантов выбора параметров приведены на рисунках 2 и 3. На рисунке 2 приведена вероятность распределения «больных» на пике заболеваемости. Пунктирной верти- кальной линией отмечена медиана распределения. Для данных, приведенных на рисунке 1, значение медианы – 53. На рисунке 2 приведена вероятность достижения времени пика заболеваемости. Вертикальной пунктирной линией отмечена медиана распределения. Для данных, приведенных на рисунке 1, пик заболеваемости произошел через 7 лет после начала эпидемии.

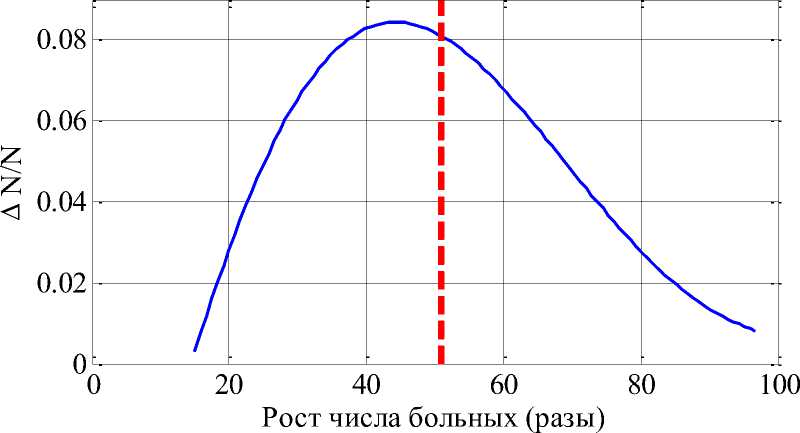
Рис. 2. Распределение вероятностей численности «больных» на пике заболеваемости

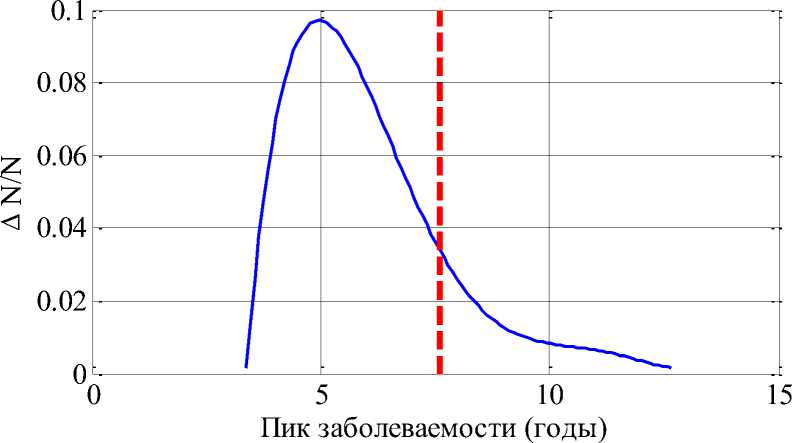
Рис. 3. Распределение вероятностей момента наступления пика заболеваемости

Таким образом, имитационное моделирование эпидемия сифилиса на основе статистических данных эпидемии 19902020 гг. прогнозирует увеличение числа

«больных» по сравнению с числом больных в начале эпидемии от 20 до 80 раз, а пик заболеваемости может достигаться через 5-8 лет после начала эпидемии. По- вторный рост заболеваемости, как след больных может длиться 15-20 лет. эпидемии, с незначительным ростом числа