Статистическое описание формирования микрогеометрии поверхности износостойких порошковых покрытий при трении скольжения

скольжения, износ, поверхность трения, теория систем порошковой среды описываются законами классической теории вероятностей и могут сопоставляться со случайными величинами микрогеометрии поверхности трения, распределение и моменты которых можно оценить обработкой профилограмм, поперечных пути трения.

Цель работы: разработка теоретиковероятностного подхода для описания микрогеометрии поверхности трения износостойкого порошкового покрытия с учетом макроструктуры порошковой среды.

Биномиальная модель для описания изнашивания сечения порошковых покрытий при трении скольжения. В работе для описания микрогеометрии поверхности трения покрытий использована элементарная модель макроструктуры порошковой среды на основе матричной вероятностно-геометрической системы частиц [1], которая ранее развита и использована авторами для моделирования изнашивания порошковых покрытий и материалов при трении скольжения [8]. Вследствие сравнительной простоты выбранная матричная вероятностно-геометрическая система позволяет рассматривать практически неограниченную порошковую среду, между тем более сложные модели допускают описание только до нескольких десятков тысяч взаимодействующих частиц. Так как сопротивление разрушению порошковой среды определяется, в основном, когезией частиц, то для учета макроструктуры при трении скольжения необходимо было связать ее характеристики с вероятностью удаления отдельной частицы на поверхности трения. В модели было предположено, что удаление частиц с поверхности трения при установившемся изнашивании является испытанием Бернулли. За событие принято удаление частицы порошкового покрытия, второе событие - что частица остается в материале, дополнительно к первому. Так как удаления частиц являются независимыми событиями с повторением испытаний, то вероятность удаления из поверхности трения к частиц будет иметь вид биномиального распределения (закон Бернулли) [8, 9]:

P i ( к ) =

l !

к !( I - к )!

Р^к (1 — Р ) l - k

где p - вероятность удаления частицы порошкового покрытия из всей поверхности трения, определяется размерами матрицы вероятностногеометрической системы; l - общее количество испытаний Бернулли [8, 9].

В предложенной модели выражение (1) описывает распределение линейного износа поперечного сечения поверхности трения порошкового покрытия; количество испытаний l соответствует пути трения. Как известно, по теореме Муавра-Лапласа при l^^ биномиальное распределение (1) стремится к нормальному [9], что соответствует известной закономерности профиля равновесной поверхности трения материалов в трибологии.

Двумерное распределение линейного износа поперечного профиля. Как установлено в многочисленных работах по трибологии, металлографические и профилометрические исследования показывают образование характерных продольных борозд по пути трения. Для описания микрогеометрии поперечного профиля поверхности порошковых покрытий разработанная модель развита в следующем направлении.

Для описания характерных борозд вдоль пути трения необходимо рассматривать взаимосвязь значений линейного износа поперечного профиля при двух значениях пути трения l и l + dl с учетом вероятностей (1). С этой целью необходимо построить двумерное распределение случайных величин к(l ) и к ( l + dl ), которые являются зависимыми. Поэтому данное распределение состоит из условных вероятностей случайной величины к(l + dl ), если при пути трения l линейный износ составлял к ( l ). Таким образом, условные вероятности задаются произведениями выражений из распределения (1). Двумерное распределение также зависит от переменных l, dl ; по его виду можно оценить взаимосвязь значений линейного износа в зависимости от пути трения. Здесь можно отметить, что приращение dl является существенно положительной величиной, поэтому увеличение пути трения в выражении (1) означает переход к последующим поперечным профилям порошкового покрытия.

В разработанной модели случайные величины к(l) и к ( l + dl ) являются дискретными; учитывая биномиальное распределение (1) и то, что линейный износ по пути трения не может уменьшаться, двумерное распределение можно выразить матрицей (табл. 1). Здесь случайная величина к ( l ) задана по столбцам, к ( l + dl ) - по строкам, также предположено l > dl . Как видно из табл. 1, матрица является прямоугольной, заполняется сложным образом: в области в виде параллелограмма расположены произведения вероятностей из выражения (1) (ненулевые ячейки матрицы указаны полужирным шрифтом); остальные элементы матрицы тождественно равны нулю.

Таблица 1. Распределение линейного износа поперечного профиля

k ( l ) k ( l + dl )	0	1	2	…	dl	…	l
0	P l (0)P dl (0)	0	0	• • •	0	• • •	0
1	P l (0)P dl ( 1 )	P l (1)P dl (0)	0	• • •	0	• ••	0
2	P l (0)P dl (2)	P l ( 1 )P dl ( 1 )	P l (2)P dl (0)	• • •	0	• • •	0
	…		…	…		• • •
dl	P l (0)P dl (dl)	P l ( 1 )P … dl (dl -1 )	P l (2)P dl (dl -2 )	…	P i (dl)P di (0)	• • •	0
dl +1	0	P l ( 1 )P dl (dl)	P l (2)P dl (dl -1 )	…	P l (dl)P dl ( 1 )	• • •	0
dl +2	0	0	P l (2)P dl (dl)	…	P l (dl)P dl (2)	…	0
				…	…	…
l + dl -1	0	0	0	• • •	0	…	P l (l)P dl (dl -1 )
l + dl	0	0	0	• • •	0	• • •	P l (l)P dl (dl)

Обсуждение результатов. На рис. 1 приведен поверхностный график двумерного распределения. Расчеты проведены при различных значениях пути трения и его приращения, разных вероятностях удаления частицы порошкового покрытия. Как видно из графика, функция имеет узкую область ненулевых значений в направлении, обусловленном ростом среднего значения линейного износа pl, вне области быстро снижается. Ненулевые значения двумерного распределения в области линейного износа свидетельствуют о том, что всегда существует корреляция координат поперечного профиля вдоль пути трения. Таким образом, распределение табл. 1 качественно описывает формирование характерных борозд на поверхности трения порошкового покрытия. При небольших вероятностях удаления частицы p функция распределена в области малых значений k(l) вследствие небольшого уровня среднего линейного износа pl.

k(l)

k(l+dl)

Рис. 1. Двумерное распределение линейного износа; путь трения l =40, dl =30, р=1/8.

Количественные характеристики двумерного распределения в табл. 1 - математические ожидания, дисперсии, среднеквадратические отклонения двух случайных величин - линейных износов k(l) и k ( l + dl ) можно рассчитать по известным общим формулам теории вероятностей [9]. В работе также использованы простые выражения для числовых характеристик двух случайных величин - математических ожиданий:

< k ( l ) >= lp

,

< k ( l + dl ) >= ( l + dl ) p

, и среднеквадратических отклонений:

^ ⁽ l ) = 4 lp ^{(1 -} p )

,

^ ( l + dl ) = V ( l + dl ) p (1 - p )

Как видно из уравнений (2), угловой коэффициент прямой линейной регрессии равен 1, тогда коэффициент корреляции линейных изно-сов двух профилей определяется простым выражением:

g(l )    _ I l

a (l + dl ) " V l + dl

Как видно из данной формулы, коэффициент корреляции не зависит от вероятности удаления частицы, а определяется текущим значением пути трения l и расстоянием между поперечными профилями dl .

На рис. 2 приведены графики зависимостей математических ожиданий и среднеквадратических отклонений линейного износа k ( l + dl) от приращения пути трения при различных параметрах расчетов: пути трения и вероятности удаления частицы. Данные, обозначенные маркерами на рис. 2, получены расчетами в MatCad, линиями - по формулам (2)-(3). Как видно из графиков и в согласии с известными формулами теории вероятностей [9] и (2), математические ожидания биномиального распределения являются линейными функциями, описываются прямыми линиями (рис. 2). Увеличение пути трения l при постоянной вероятности удаления частицы p приводит к параллельному смещению прямой линии вверх. Среднеквадратическое отклонение случайной величины k ( l + dl ) с биномиальным распределением, как видно из (3), изменяется по зависимости ~(l + dl) ¹/² [9], увеличение пути трения и вероятности удаления приводят к его росту (рис. 2).

Далее, для количественной оценки взаимосвязи линейного износа при значениях пути трения l и l + dl можно вычислять коэффициент корреляции случайных величин k(l ) и k(l + dl ) по найденному распределению (табл. 1) с формулой теории вероятностей [9]. На рис. 3 приведены графики зависимостей коэффициента корреляции линейных износов поперечных профилей от приращения пути трения.

Следует отметить, что приращение пути трения означает расстояние между двумя поперечными профилями. Расчеты также проведены при различных значениях пути трения и вероятности удаления частицы порошкового покрытия. Данные, обозначенные маркерами на рис. 3, также получены расчетами в MatCad, линиями -по формуле (4). Как видно из графиков 1, 7, 6 на рис. 3, коэффициент корреляции не зависит от вероятности удаления частицы, что согласуется с формулой (4). При малых значениях пути трения с увеличением приращения dl коэффициент корреляции снижается (рис. 3). Это означает, что линейные износы k(l ) и k ( l + dl) поперечных сечений в начале пути трения слабо коррелируют.

Однако, как видно из графиков, увеличение пути трения приводит к росту коэффициента корреляции. Данная закономерность отражает форми- статистическая модель изнашивания покрытий, учитывающая макроструктуру порошковой среды, позволяет качественно описывать формиро- рование характерных борозд вдоль пути трения вание микрогеометрии поверхности трения по-

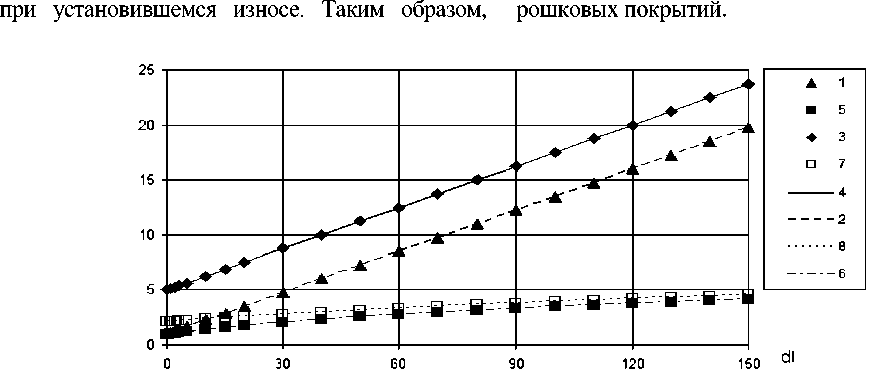
Рис. 2. Характеристики линейного износа - математические ожидания: 1,2- L=8, p=1/8;3,4- L=40, p=1/8; среднеквадратические отклонения: 5,6- L=1/8, p=1/8;7,8- L=40, p=1/8

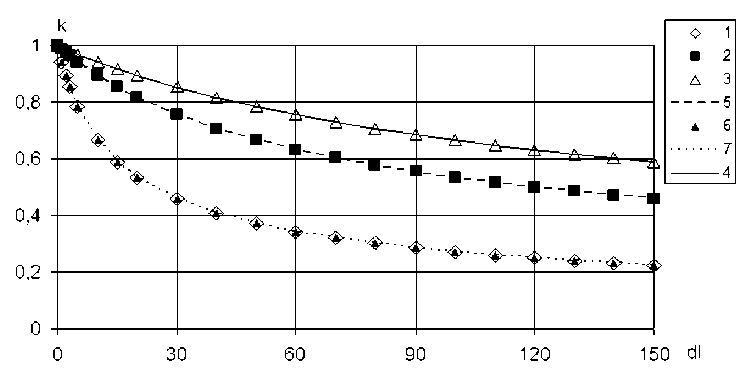
Рис. 3. Коэффициент корреляции линейных износов поперечных профилей;

1,7- L=8, p=1/8; 2,5- L=40, p=1/8; 3,4- L=80, p=1/50; 6- L=8, p=1/50

Выводы:

• 1.    Разработан статистический подход для описания микрогеометрии поверхности трения износостойкого порошкового покрытия, учитывающий случайную макроструктуру порошковой среды. При этом использована матричная вероятностно-геометрическая модель сечения порошкового покрытия.

• 2.    Характерные борозды на поверхности трения описываются взаимосвязью значений линейного износа поперечного профиля, распределенных по биномиальному закону. Вычислениями условных вероятностей линейного износа поперечного профиля построено их двумерное распределение, зависящее от пути трения.

• 3.    Проведены расчеты математических ожиданий, среднеквадратических отклонений и коэффициентов корреляции линейного износа. Показано, что разработанный статистический подход качественно описывает характерную микрогеометрию поверхности трения порошковых покрытий.

Работа проведена при поддержке Российского Фонда Фундаментальных исследований (грант № 12-0898500).