Стеклянно-полимерные микрофлюидные чипы для электрофоретического разделения биомолекул

Развитие и совершенствование технологий и методов оперативного создания микрофлюид-ных чипов (МФЧ) вызывает неослабевающий интерес исследователей, т. к. позволяет изготавливать микрочипы в условиях лабораторий, не оснащенных специализированным оборудованием. Особое внимание уделяется методам "мягкой" литографии (soft lithography) термоотверждаемых полимеров [1, 2]. Наиболее используемым материалом для быстрого макетирования микрофлю-идных чипов является полидиметилсилоксан (ПДМС), в частности Sylgard 184 ( Dow Corning Corporation , США) [3]. Для создания микрораз-мерных структур в этом материале требуется мастер-форма, которая может быть изготовлена в организации, где есть необходимое оснащение для методов фотолитографии. Важными задачами при создании МФЧ являются: обеспечение герметичности микроканалов и реакционных камер; модификация рабочей поверхности ПДМС с целью придания необходимых свойств (например, регулирования и стабилизации электроосмотического потока). Для этого используется ряд физикохимических методов, которые и рассматриваются в данной статье.

Реализация методов электрофоретического разделения биологических проб на МФЧ позволяет достигнуть ряда дополнительных преимуществ по сравнению с классическим методом капилляр- ного электрофореза: сверхмалые объемы анализируемой пробы и дорогостоящих реагентов, высокая скорость анализа, низкое энергопотребление. Поэтому, развитию и совершенствованию методов электрофореза на МФЧ до сих пор уделяется внимание многих исследователей [4, 5]. В работе обсуждается вариант гибридного (стеклянно-полимерного) микрофлюидного чипа для электрофоретического разделения биомолекул и приводятся результаты его апробации при разделении смеси олигонуклеотидов, меченных FITC (Fluorescein isothiocyanate).

ИЗГОТОВЛЕНИЕ ПРОТОТИПА СТЕКЛЯННО-ПОЛИМЕРНОГО МИКРОФЛЮИДНОГО ЧИПА

Процесс создания аналитического МФЧ включает стадии: выбора материалов; разработки топологии и конструкции микрочипа; изготовления микро- и наноразмерных структур; обработки поверхности; герметизации конструкции; контроля и испытаний готового устройства.

В качестве материалов для изготовления прототипов МФЧ применялись:

• •    стекло марки Крон 8 (К8) (ГОСТ 3514-76, Россия);

• •    ПДМС марки Sylgard® 184 ( Dow Corning Corporation , США).

  а

  
  
  

  б

  

  Рис. 1. Прототип МФЧ.

  На эскизе топологии МФЧ (а): Р 1 –Р 5 — резервуары для загрузки пробы и буферного раствора, О 1 и О 2 — пересечения каналов. На изображении герметизированного МФЧ (б): 1 — стеклянная подложка, 2 — пленка ПДМС с системой каналов и резервуаров

  
  

На основании анализа литературных данных была выбрана универсальная топология, объединяющая в себе топологии "Т-инжектор" и "простой крест" [6].

С учетом приборных особенностей (имеющейся системы детектирования, расположения рабочих электродов и необходимой длины сепарационного канала) были определены соответствующие размеры, которые явились основой для топологии мастер-формы, состоящей из трех секций для получения трех реплик из полимера. Эскиз одной секции приведен на рис. 1, а, где О 1 Р 1 = О 1 Р 3 = О 2 Р 2 = О 2 Р 4 = 3.9 мм; О 1 О 2 = 0.5 мм; О 2 Р 5 = 41.0 мм; ширина каналов 60 мкм; диаметр резервуаров для загрузки пробы и слива отработанного раствора 2 мм. Высота полученных на мас-тер-форме структур контролировалась на профилометре Ambios Technology (США) и составила 18 ±1 мкм.

На основании данной топологии методом фотолитографии была изготовлена мастер-форма из кремния и фоторезиста SU-8 2025 ( MicroChem Corp ., США) в Академическом университете — Научно-образовательном центре нанотехнологий РАН (Санкт-Петербург).

Методом "мягкой" литографии [7] осуществлялось получение отпечатков структур в ПДМС, основанное на отверждении раствора полимера, помещенного поверх мастер-формы. Затем проводилась герметизация сформированных микрораз-мерных структур посредством соединения отпечатка (реплики) из ПДМС (размером 54×14×2 мм)

со стеклянной пластиной (стекло К8, размером 60×15×1.5 мм) после их обработки высокочастотной (13.56 МГц) плазмой в среде кислорода при давлении ≈1 мбар на установке Diener Zepto (Германия). Изображение готовой конструкции МФЧ приведено на рис. 1, б.

Для мастер-формы на оптическом инвертированном микроскопе Axio Observer.D1m ( Carl Zeiss , Германия) была измерена ширина каналов в двух крайних точках сепарационного канала О 2 , Р 5 . Для реплик из ПДМС контролировались ширина и глубина каналов. Измерения проводились на оптическом инвертированном микроскопе с объективом 20^х. Было рассчитано среднее значение ширины каналов по трем репликам, среднее квадратичное отклонение (СКО) и оценен коэффициент вариации (КВ). В области Р 5 среднее значение ширины составило 63.5 мкм, СКО — 4.2 мкм, КВ — 6.6 % при заданной ширине канала на мастер-форме 61.3 мкм.

ИССЛЕДОВАНИЕ ФИЗИКО-ХИМИЧЕСКИХ МЕТОДОВ И ВЫБОР УСЛОВИЙ ОБРАБОТКИ ПОВЕРХНОСТЕЙ В ПДМС

Целесообразность исследований физико-химических методов модификации ПДМС продиктована необходимостью придания поверхности гидрофильности, уменьшения степени адсорбции биомолекул, создания функциональных слоев (иммобилизация гелевых сред, ферментов, сенсорных слоев) и др. Трудности при обработке по- верхности связаны с тем, что в процессе отверждения полимера непрореагировавшие компоненты, обладающие высокой подвижностью, диффундируют к поверхности, что вызывает восстановление гидрофобных свойств полимера после обработки. Например, плазменная обработка в различных средах, часто применяемая для создания герметичных конструкций МФЧ, не позволяет получить стабильные во времени свойства поверхности. Поэтому обработка плазмой является лишь предварительным этапом подготовки поверхности к последующему осаждению (из газовой среды или растворов) различных функциональных слоев. В частности, при изготовлении МФЧ для электрофоретического разделения проб необходимым условием для получения воспроизводимых результатов при разделении компонентов является стабилизация электроосмотических свойств, которую можно достичь различными методами физико-химической модификации поверхности.

Все это является мотивацией исследований, направленных на выбор эффективных методов модификации, позволяющих получать требуемые (в зависимости от решаемых задач) стабильные во времени свойства поверхности. Например, в некоторых случаях для разделения нуклеиновых кислот необходимо создать условия для достижения низких значений электроосмотического потока.

Были исследованы следующие способы обработки и модификации открытых поверхностей ПДМС, а также каналов МФЧ:

• 1)    высокочастотной (13.56 МГц) плазмой в среде кислорода (1.5 мин) и аргона (1 мин) при низком давлении ≈1 мбар (установка Diener Zepto, Германия);

• 2)    1 % водным раствором поливинилового спирта (ПВС) ( Sigma-Aldrich Corp ., США);

• 3)    3 % водным раствором Kolliphor ( Sigma-Aldrich Corp ., США).

За основу обработки раствором поливинилового спирта каналов МФЧ для электрофоретического разделения проб была принята методика, описанная в работе [8]. Предварительная обработка плазмой в среде кислорода придает не только выраженные гидрофильные свойства, но и вызывает образование на поверхности различных функциональных групп и свободных радикалов (в том числе С–ОН, Si–OH, СООН и др.). Таким образом, за счет образования водородных связей происходит адсорбция слоя ПВС из водного раствора на обработанную плазмой поверхность ПДМС.

Другим способом, позволяющим снизить краевой угол, а также влияющим на поверхностный заряд, образующийся на стенках канала МФЧ и вызывающий образование слоя противоионов из буферного раствора, является модификация раствором Kolliphor. Обработка аналогичным линейным сополимером описана в [9]. В основе механизма закрепления слоя полимера лежит образование свободных радикалов на поверхности ПДМС в процессе плазменной обработки в среде аргона. Некоторые из этих радикалов взаимодействуют с радикалами, образованными в плазме, что приводит к появлению на поверхности функциональных групп. Активированная таким образом поверхность может реагировать с кислородом или влагой, содержащимися в воздухе, образуя группы SiO2, Si–OH или Si–CH2OH на поверхности ПДМС. После плазменной обработки образцы (полимерные пленки и МФЧ) выдерживались в водном растворе Kolliphor в течение 24 ч при температуре 60 °С для адсорбции на поверхности тонкой пленки.

Метод лежащей капли позволил изучить влияние физико-химических способов обработки на свойства смачивания открытой поверхности ПДМС дистиллированной водой. Измерения краевого угла проводились с помощью экспериментальной установки на базе оптического микроскопа PrimaExpert (ЛОМО, Россия). Для каждого образца было выполнено по 6–8 измерений краевого угла при объеме капли воды 20 мкл.

Оценку величины µ ЭОП подвижности электроосмотического потока (ЭОП) при использовании буферного раствора (50 мМ Na 2 B 4 O 7 , pH = 9.4) в зависимости от способа обработки осуществляли на экспериментальных образцах микрофлюидных чипов с помощью микрофлюидной аналитической системы МФАС-01 (ИАП РАН, Санкт-Петербург). Величину µ ЭОП определяли по методу, описанному в работе [10], и по формуле:

L⋅L µЭОП =U⋅∆t , где L — длина сепарационного канала (L = 45.2 мм), U — напряжение электрофореза (U = 1000 В), Δt = t2 – t1 — время изменения величины тока, которое определялось экспериментально.

Результаты расчетов средней величины краевых углов, а также электроосмотической подвижности буферного раствора в каналах МФЧ (по данным 6–7 измерений Δ t для каждого микрочипа) в зависимости от способа обработки с указанием среднего квадратичного отклонения и оценки коэффициента вариации приведены в табл. 1.

Согласно данным табл. 1, следует сделать вывод о нестабильности свойств поверхности каналов микрочипа после плазменной обработки, о чем свидетельствуют наибольшие значения погрешностей. Наиболее эффективным способом модификации микрочипов с точки зрения получения

Табл. 1. Величины краевых углов ( θ ) образцов пленок ПДМС, µ _ЭОП буферного раствора в каналах МФЧ в зависимости от способа обработки

Характеристика	Необраб.	Обработка плазмой в среде О 2	Обработка раствором ПВС	Обработка плазмой в среде Ar	Обработка раствором Kolliphor
Средн. знач. θ ±СКО (град)	107±1	˂10	61±2	≈20	39±4
Оценка КВ θ (%)	1	–	3	–	10
Средн. знач. μ ±СКО ( см2 /(В ⋅ с) ⋅ 104 )	3.0 ±0.2	4.1 ±0.6	2.1 ±0.1	–	1.8 ±0.1
Оценка КВ μ (%)	7.5	14.9	5.6	—	4.1

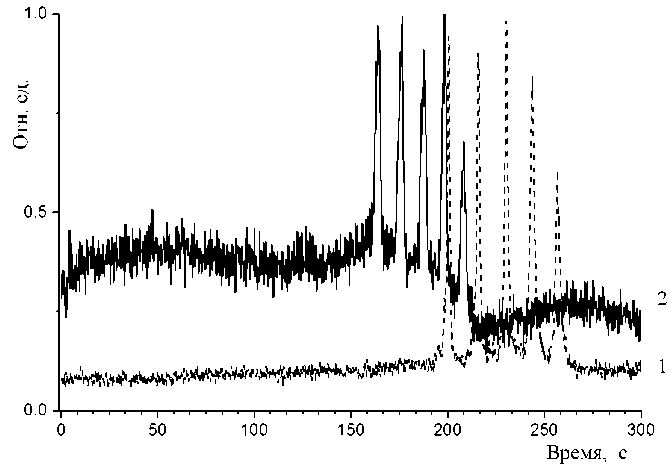
Рис. 2. Электрофореграмма разделения смеси олигонуклеотидов.

1 — зависимость для необработанного микрочипа; 2 — для обработанного раствором Kolliphor (пики нумеруются слева направо и соответствуют компонентам 10, 20, 30, 40 и 50 оснований)

наименьшего значения краевого угла и наименьшей величины ЭОП оказалась обработка раствором Kolliphor. Уменьшение ЭОП желательно. Суммарная результирующая подвижность компонентов при электрофорезе есть разность электрофоретической и электроосмотической подвижностей.

Таким образом, именно обработка раствором Kolliphor была выбрана для модификации микрочипов с целью их тестирования при разделении смеси олигонуклеотидов.

ЭЛЕКТРОФОРЕТИЧЕСКОЕ РАЗДЕЛЕНИЕ СМЕСИ ОЛИГОНУКЛЕОТИДОВ НА СТЕКЛЯННО-ПОЛИМЕРНОМ ЧИПЕ

Для электрофореза на микрочипах в качестве анализируемой пробы была выбрана смесь олигонуклеотидов (полиаденилатов) с длиной цепи 10, 20, 30, 40 и 50 нуклеотидов с флуоресцентной меткой. Электрофорез проводился на микрофлю-идной аналитической системе МФАС-01 с детектором лазер-индуцированной флуоресценции (длина волны возбуждения 473 нм, регистрации — 510–530 нм, напряжение электрофореза 1500 В). В качестве буферного раствора использовался 6 % раствор полидиметилакриламида с добавлением 7 М мочевины. Результаты разделения исследуемой пробы приведены на рис. 2. Зависимости нормированы относительно максимального значения интенсивности флуоресценции.

Согласно полученным зависимостям, можно оценить время, необходимое для проведения электрофоретического разделения смеси олигонуклеотидов. Для необработанного микрочипа (нижняя зависимость) это время составило ≈275 с, тогда как для обработанного раствором Kolliphor (верхняя зависимость) около 220 с. Таким образом, уменьшение величины электроосмотического потока позволяет сократить время разделения пробы.

МОДЕЛИ ИНФОРМАТИВНЫХ СИГНАЛОВ (ЭЛЕКТРОФОРЕТИЧЕСКИХ ПИКОВ) И МОДЕЛЬ

СЛУЧАЙНОЙ СОСТАВЛЯЮЩЕЙ СИГНАЛА

Пики олигонуклеотидов 10, 20, 30, 40 и 50 оснований для обработанных раствором Kolliphor и необработанных поверхностей адекватно аппроксимируются зависимостями вида

У ( x ) = У 0 + — exp f- 2 ⁽ x x c ) ^ ,       (1)

w V n /2    ( w )

где y0 — локальный уровень фонового сигнала; w/2 — корень из дисперсии (стандартное отклонение); xc — центр тяжести пика; x — отсчеты сигнала (интервал отсчетов равен 0.2 с); амплитуда пика равна A,(w^n /2); w также измеряется в отсчетах.

Параметры моделей пиков и квадрат выборочного коэффициента корреляции R как характеристика адекватности модели приведены в табл. 2.

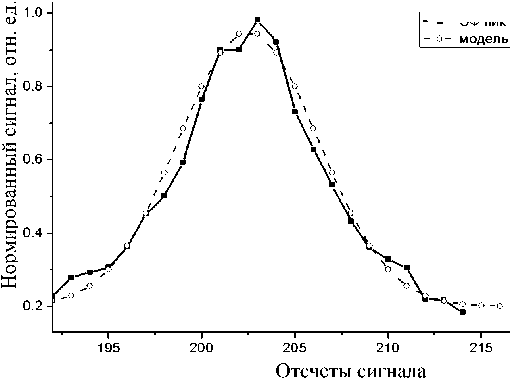
Данные табл. 2 позволяют утверждать, что качество аппроксимации очень высокое. Пример аппроксимирующей зависимости для пика 3 (30 оснований) для необработанного МФЧ приведен на рис. 3. Аппроксимация остальных пиков моделями (1) имеет качественно схожий вид. Во всех случаях сигнал приведен к нормированному виду относительно максимума. Отношение величины фона и амплитуды пика ( y ₀ / A ) для МФЧ, обработанного раствором Kolliphor, по крайней мере вдвое большее по сравнению с необработанным.

Табл. 2. Параметры математических моделей (1) электрофоретических пиков при различных способах обработки поверхностей материалов

Пик	R 2	A	w	x c	y 0	Способ обработки
1	0.9760	5.5801	6.1113	1003.35	0.2042	Необработанный
2	0.9802	5.4413	6.4649	1080.18	0.2298
3	0.9846	6.3828	7.0676	1152.55	0.2157
4	0.9842	7.9662	10.563	1219.51	0.1869
5	0.9687	5.9027	12.120	1285.75	0.1488
1	0.9222	6.8571	11.070	820.07	0.4430	Обработанный рас-
2	0.9114	9.4332	12.745	879.41	0.3399	твором Kolliphor
3	0.9537	11.225	14.951	937.72	0.2625
4	0.9290	7.9503	10.487	991.62	0.3330
5	0.9495	4.6415	10.382	1041.11	0.2972

—■—ЭФ-пик

Рис. 3. Аппроксимация пика 3 (для необработанного МФЧ) зависимостью (1) (нумерация отсчетов сигнала уменьшена на 950)

Анализ связи между x_c — временными положениями центров тяжести (временами выхода) пиков компонент для обработанного и необработанного МФЧ дает высокую корреляцию: оценки выборочного коэффициента корреляции и его медианного аналога равны соответственно 0.99992 и 0.99974. Это свидетельствует об очень сильной линейной связи между временами выхода соответствующих компонент и о линейной связи между соответствующими подвижностями (электрофоретической и электроосмотической). Т. к. также наблюдается пропорциональность времен выхода (коэффициент близок к 0.81), то это может означать соответствующее пропорциональное сокращение продолжительности всех стадий анализа от загрузки пробы до электрофоретического разделения.

Начальная фаза сигнала (порядка 180 с для необработанного и 140 с для обработанного МФЧ) заведомо не содержит аналитических пиков, и ее можно использовать для анализа случайной неинформативной составляющей сигнала. В первом случае математическое ожидание и стандартное отклонение равны соответственно 0.0924 и 0.0137; во втором — 0.3811 и 0.0379. Имеющаяся систематическая составляющая (дрейф фонового сигнала) в виде линейного тренда по критерию Фишера незначима.

Для анализа закона случайной составляющей применен критерий согласия Пирсона (хи-квадрат-критерий). В обоих случаях гипотеза о нормальном (гауссовом) характере распределения принимается с высокой вероятностью: около 83 и 72 %. Тем самым можно полагать, что среди факторов, формирующих случайную погрешность, нет доминирования какого-либо одного. Т. е. все составляющие погрешности сопоставимы друг с другом по вкладу.

Следующий вопрос — достаточность отсчетов для идентификации пика компонент. Если использовать в качестве критерия практически достоверной дискриминации фон/пик разность величин, равную или превышающую 4 σ , то каждый из рассмотренных в табл. 2 пиков содержит не менее 14-ти отсчетов, что представляется достаточным. Пороговый уровень 4 σ расхождения (фон—начало или конец пика) при нормальном законе распределения соответствует вероятности ошибки определения начала (конца) пика менее 0.25 %.

АНАЛИЗ БАЗОВЫХ ТЕОРЕТИЧЕСКИХ ПОЛОЖЕНИЙ, СВЯЗАННЫХ

С КОНВЕКТИВНО-ДИФФУЗИОННЫМ ПЕРЕНОСОМ ВЕЩЕСТВА В МИКРОЧИПЕ

Анализ модельной формы конвективного скоростного профиля может основываться на оцени- вании размывания пиков компонент. Т. к. профиль формируется не гидравлическим, а электрофоретическим (электроосмотическим) способом, то модельный профиль полагаем следующего вида: в пристеночных областях скорость меняется по линейному закону от нуля до максимальной величины, на остальной области она максимальная и постоянна. Эта зависимость имеет вид:

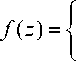
U ( z ) = V * • f ( z ), 1,          0 <  z <  1 - 5 ;           (2)

(1 -z)/5, 1 -5 < z < 1, где V* — максимальная скорость; z — относительная ширина канала, отсчитываемая от оси и нормированная на полуширину h .

Задача состоит в оценивании пристеночной длины ( δ ) и сопоставлении ее с длиной Дебая.

Основой расчетов будут служить ранее найденные зависимости центра тяжести пика и средней по сечению дисперсии пика для случая микроканала — совокупности плоских щелей одинакового размера [11]. Необходимо разложение в ряд +y

Фурье профиля (2): f ( z ) = B ⁰ + £ B^J cos( n jz ).

j = 1

Тогда усредненные по сечению координаты центра тяжести и дисперсии пика равны x_c = u B ⁰ t и

(        +™

(а ²) = 2 + Pe ² £

к

j = 1

^B )

(nJ )² J

D * t +

+

А 2 - 3 Pe 2 f J^jl_ I 3 2 ^£ 1 (nj ) 4 J

.

к

Здесь центр тяжести и корень из средней дисперсии приведены к длинам, нормированным на полуширину канала h ; коэффициент диффузии D и максимальная скорость V ^* преобразованы к безразмерному виду u * = V * / h и D * = D / h ²; А — приведенная длина пробки, равная для нашей схемы загрузки 1; число Пекле Pe = u * / D * . Значения скоростей определяются по соответствующим электрофореграммам (рис. 2), а коэффициенты диффузии олигонуклеотидов от 10 до 50 оснований определены по экстраполяции данных работы [12]. Однако, поскольку в [12] наименьшая длина рассматриваемого фрагмента была 100 оснований, то эта экстраполяция может быть неправомерна для самых коротких фрагментов — 10 и 20 оснований. Таким образом, для дальнейшего моделирования профилей (2) использованы только по 3 пика фрагментов 30, 40 и 50 оснований.

Пересчет дисперсий пиков из табл. 2 в безразмерные длины позволяет сопоставить их с форму- лами (3) и подобрать итерационным методом значение характерной нормированной пристеночной толщины δ . Результаты приведены в табл. 3.

Величина δ выбрана по критерию минимального расхождения стандартных отклонений пиков 3–5 между электрофореграммой и моделью (2). Таким образом, для необработанного чипа характерная глубина δ в абсолютном выражении составляет 0.6 мкм, для обработанного раствором Kolliphor — вдвое большая, т. е. 1.2 мкм. Согласно формальной модели (2), конвективный скоростной профиль меняется только вблизи стенки канала на протяжении порядка 0.6–1.2 мкм, а далее стабилизируется.

Одним из возможных объяснений может быть следующее: при обработке раствором Kolliphor в пристеночной области на границе (твердая стенка—буфер) появляется слой полимера, который может видоизменяться при контакте с буферным раствором. По-видимому, этот слой дополнительно увеличивает толщину пристеночной области.

Следует заметить, что параметры электрофоретического пика были взяты, исходя из гауссовой аппроксимации, адекватность которой подтверждена корреляционным анализом.

Однако, предложенная нами модель (2) носит формально-описательный характер. Далее сопоставим с ней физическую модель распределения скоростного профиля в прямоугольном канале, базирующуюся на уравнении Пуассона—Больцмана.

Уравнение Пуассона—Больцмана представим d ² ^ 2 Flc₀ f 1,вф( z ) )

в форме —у =---‘""°" sh ~----- , где l — валент- dz2     s ( kbT } ность i-го иона; е — заряд электрона (1.6.10–19 Кл), F — постоянная Фарадея (9.65.104 Кл/моль); с0 — молярная концентрация ионов компонент (моль/м3); Т — температура (К); kb — постоянная Больцмана (1.38.10–23 Дж/К); φ — потенциал, z — нормированная пространственная координата сечения; sh — функция гиперболического синуса, в ряде случаев допускает линеаризацию в форме приближения Дебая—Хаскела. Гиперболический синус заменяется своим аргументом, и уравнение сводится к линейному дифференциальному уравнению второго порядка с решениями — гиперболическими функциями. Характерным масштабом расстояния является дебаевская длина ID =

ε ₀ εkT

2 li ² F ² c ^,

составляющая порядка 10 нм [13].

Толщина двойного электрического слоя составляет несколько λD. В частности, в [14] говорится о четырехкратной дебаевской длине, в [15] упоми- нается о единицах–десятках нм по сравнению с микрометровыми размерами канала.

Тогда применительно к плоской или прямоугольной щели электроосмотическая составляющая конвективного скоростного профиля описывается как u (z) = V *

1 -

ch( αz ) ch( α )

где коэффициент пропорциональности α выражается по-разному, но обратно пропорционален дебаевской длине [16, 17].

Сопоставив формальную математическую модель (2), оценки (3) и выражение (4) по принципу эквивалентного размывания пиков; получим, что для необработанного МФЧ соответствующее значение α примерно 99.5, для обработанного — 43. Так как по смыслу величина, обратная α , аналогична пристеночной толщине δ , то в абсолютных величинах характерными расстояниями будут соответственно 300 и 600 нм. Эти расстояния по крайней мере на порядок отличаются от толщины двойного электрического слоя, но малы по сравнению с полушириной микроканала.

Табл. 3. Моделирование конвективного скоростного профиля (2) на основе характеристик пиков олигонуклеотидов 30, 40 и 50 оснований для необработанного и обработанного МФЧ

Способ обработки	Пик	Время выхода, с	Станд. отклонение пика, нормированное h		δ
			Электрофореграмма	Модель
Необработанный	3	230.5	4.7	6.2	0.020
	4	243.9	6.6	5.9
	5	257.2	7.1	5.9
Обработанный раство-	3	187.5	11.2	8.6	0.040
ром Kolliphor	4	198.0	7.6	9.1
	5	208.0	7.1	9.6

ЗАКЛЮЧЕНИЕ

Проведенные исследования позволяют утверждать, что выбранный способ обработки поверхностей стеклянно-полимерного МФЧ раствором Kolliphor позволяет стабилизировать и уменьшить электроосмотический поток, тем самым примерно на 20 % повысить экспрессность анализа смеси олигонуклеотидов (с 275 до 220 с). При этом а) информативный сигнал (совокупность пиков компонент) практически не меняет своих характеристик (высокая вероятность разрешения соседних пиков, малая вариация ширины и амплитуды пика); б) достаточное число измерений (не менее 14), приходящихся на каждый пик позволяет уверенно их распознать на фоне случайного сигнала; в) фоновый сигнал представляет собой малозначимый (по критерию Фишера) систематический линейный тренд и гауссовую случайную составляющую; г) при обработке поверхностей раствором Kolli-phor средний уровень фонового сигнала увеличивается в 2–2.5 раза (от 0.15–0.23 для необработанного чипа до 0.27–0.44 для обработанного раствором), что может быть связано с изменением физико-химических характеристик поверхности (см. динамику величин краевых углов в табл. 1).

Высокая вероятность (более 70 %) принятия гипотезы о нормальном (гауссовом) характере случайной составляющей сигнала позволяет утверждать, что формируемая погрешность не имеет преобладающего (доминирующего) источника.

Рассматриваемая формальная модель (2) профиля конвективной скорости в микроканале позволяет предположить изменения скорости от нулевой (прилипание к стенкам) до максимальной лишь в малой пристеночной области (порядка сотен нм). Эти толщины примерно на 1–1.5 порядка превосходят оценки толщины двойного электрического слоя. Однако формальная модель (2) хорошо сочетается с теоретически обоснованной зависимостью (4). При подборе эквивалентных параметров моделей одновременно удается согласовать как положение центра тяжести, так и дисперсию пиков. Рассматриваемые режимы переноса характеризуются доминированием конвективной составляющей над диффузионной (числа Пекле в диапазоне 40–180).

Итак, способ обработки поверхностей стеклян-но-полимерного микрофлюидного чипа, включающий применение раствора Kolliphor, позволил стабилизировать электроосмотический поток и уменьшить его величину, что обусловило примерно на 20 % уменьшение времени электрофоретического разделения смеси олигонуклеотидов 10, 20, 30, 40 и 50 оснований без существенного ухудшения идентификации пиков компонент, т. е. характеристик информативного сигнала.

Работа выполнена в рамках программы Фундаментальных исследований Президиума РАН № 9 "Создание и совершенствование методов химического анализа и исследования структуры веществ и материалов", проект "Микрофлюидные чипы для анализа биомолекул методами электрофореза" и при частичной государственной финансовой поддержке ведущих университетов Российской Федерации (субсидия 074-U01).

Авторы выражают особую признательность канд. физ.-мат. наук А.С. Букатину (АУ-НОЦ нанотехнологий РАН) за оперативное изготовление мастер-форм для МФЧ.