Stochastic Leontieff type equations and mean derivatives of stochastic processes

In papers [1, 2] a new approach to investigation on dynamically distorted signals is suggested that is based on Leontieff type differential equations. Further development of this approach requires taking interference (noise) into account that yields the transition to Stochastic Differential Equations. Here the correspondent stochastic differential equation takes the form

^^                    ^^

L£ ( t ) = M

j £ ⁽ s ) d

s + f ( t ) + Bw( t ) ,

where L is a, degenerate matrix n x n. M and B are non-degenerate matrices n x n. £ ( t ) is an n -dimensional stochastic process, f ( t ) is a smooth n -dimensional vector-function and w ( t ) is a Wiener process in R ⁿ. The physical meaning of these objects is as follows: f ( t ) is the signal incoming into the device described by the matrices L and M , while Bw(t ) (where w ( t ) is « derivative » of Wiener process, i.e., white noise) describes the noise (interference).

The equations of such sort are called the Leontieff type stochastic differential equations.

The features of Leontieff type equations require dealing with the derivatives of f ( t ) and w ( t ) of any order. In paper [3] in the simplest case, where the incoming signal is absent, B is the unit matrix and the equation has been reduced to canonical form, the so called current velocities (symmetric mean derivatives) of Wiener process are involved for describing the derivatives of Wiener process. As a result some physically reasonable analytical formulae for the solutions are obtained.

Ю.Е. Гликлих, Е.Ю. Машков

The notion of mean derivatives was introduced by E. Nelson [4, 5, 6] for the needs of the so-called Nelson’s stochastic mechanics (a version of quantum mechanics). Later a lot of applications of mean derivatives to some other branches of science were found. The investigation of Leontieff type stochastic differential equations is a new field of application of mean derivatives. Note that by general ideology of the theory of Nelson’s mean derivatives the current velocities are natural analogues of physical velocity of deterministic processes.

In this paper by the use of current velocities we investigate the general situation and do not suppose the equation to be already reduced to canonical form. Some constructions connected to reducing the equations to canonical form are announced in [7].

An alternative approach to investigation of Leontieff type stochastic equations, also based on the use of current velocities, is suggested in [8].

Besides the Introduction the paper contains three Sections. The first one is devoted to basic preliminary fact from the theory of mean derivatives necessary for the purpose of this article. In Section 2 we investigate the transition of Leontieff type stochastic differential equations to canonical form. In Section 3 we find formulae for the solutions of equations under consideration.

Throughout the paper we use Einstein’s summation convention with respect to shared upper and lower indices.

We refer the reader to [9, 10] for details on the machinery of mean derivatives.

The research is supported in part by RFBR Grants 10-01-00143 and 12-01-00183.

1.    Preliminaries on the mean derivatives

Consider a stochastic process £ ( t ) in R n, t E [0 , l ], given on a certain probability space (Q , F, P) and su

£ ( t ) is L 1-random variable for all t.

Every stochastic process £ ( t ) in R n, t E [0 ,l ], determines three families of ст -subalgebras of ст -algel>ia F;

• (i)    the « past » P¹ generated Irv pre-images of Borel sets in R ⁿ Irv all irtappings £ ( s ) : Q ^ R ⁿ for 0 < s < t;

• (ii)    the « future » F¹ generated Irv pre-images of Borel sets in R ⁿ Irv all mappings £ ( s ) : Q ^ R ⁿ for t < s < l;

• (iii)    the « present » (« now ») N generated Irv pre-irnages of Borel sets in R ⁿ Irv the mapping £ ( t )-

• All families are supposed to be complete, i.e., containing all sets of probability 0.

For convenience we denote the conditional expectation of £ ( t ) with respect to N¹ bу Et ( • ).

Ordinary ( « uncondilioiml » ) expectation is denoted by E.

Strictly speaking, almost surely (a.s.) the sample paths of £ ( t ) are not differentiable for almost all t. Thus its « classical » derivatives exist only in the sense of generalized functions. To avoid using the generalized functions, following Nelson (see, e.g., [4, 5, 6]) we give

Definition 1. (i) Forward mean derivative Df ( t ) оft ( t ) at time t is an Li-random variable of the form

D^ (t )= lim E| (^(t + A t) ~ ^(t))(1)

• s v '   дt»+0 tv        At'

where the limit is supposed to exists in L i(Q , F, P) and A t ^ +0 means that A t tends to 0 and A t >  0.

• (ii)    Backward mean derivative D*^ ( t ) о ft ( t ) a11 is an Li-random variable

D^ (t ) = Jim E (^(t' - At^ A t')<21

where the conditions and the notation are the same as in (i).

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ

Note that mainly D£ ( t ) = D*£ ( t ), but if, say, £ ( t ) a.s. has smooth sample paths, these derivatives evidently coinside.

From the properties of conditional expectation (see [11] ) it follows that D£ ( t ) and D*£ ( t ) can be represented as compositions of £ ( t ) and Borel measurable vector fields (regressions)

Y 0( t,x ) = lim E ( f ( £ ±^ t ) ^M|£ ( t ) = x ) ^v , ’   д t^ +0 ^v       A t

Y 0( t,x )= lim E ( ^£^LJ⁽L_|£ ( t ) = x )

* v , ' дt^+0 v        At on Rn. This means that D£(t) = Y0(t,£(t)) aiid D*£(t) = Y*o(t, £(t)).

The derivatives introduced in Definition 1, is a particular case of the objects defined as follows. Let x ( t ) aiid y ( t ) be L i-stochastic jprocesses in R n. given on (Q , F, P). Intrc)duce y -forward mean derivative of x ( t ) lay the formula,

Dy x (t )= lim Ey (x(t ± A')   x(t))( 4 )

v '   д t-++0             At'

and y -backward mean derivative of x ( t ) lay the formula

Dy x (t ) = д!™0 E (x1 t^ A^ A t')

where the limits must exist in L i(Q , F, P).

Recall that a process £ ( t ) is called martingale (in о nr case - with respect its « past » Ptb ^ for every time instants 0 < s < t < l the relation E ( £ ( t ) | Pl ) = £ ( s ) takes place.

Lemma 1. Let £ ( t ) be a martingale with respect to its «past» P¹. Tllen D£ ( t ) = 0.

Proof. By the properties of conditional expectation E¹ ( E ( • | P¹ )) = Et ( • ). Then E¹ ( £ ( t ± A t ) — £ ( t )) = E| ( E ( £ ( t ± A t ) — £ ( t ) Ф,¹ )) = E, ( £ ( t ) — £ ( t )) = 0                                      _Q

Definition 2. The derivative D s = 2( D ± D* ) is called symmetric mean derivative. The derivative D a = 2( D — D* ) is called anti-symmetric mean derivative .

Consider the vector fields v¹ ( t,x ) = 2( Y ⁰( t,x ) ± Y* ^o( t,x )) and u¹ ( t,x ) = |( Y ⁰( t,x ) — ^Y* ^{0( t,x} ))-

Definition 3. v¹ ( t ) = v¹ ( t,£ ( t )) = D s £ ( t ) is called current velocity o/ £ ( t ); u¹ ( t ) = u¹ ( t,£ ( t )) = D a £ ( t ) is called osmo tic velocity of £ ( t ).

For stochastic processes the current velocity is a, direct analogue of ordinary physical velocity of deterministic processes (see, e.g., [4, 5, 6, 9, 10]). The osmotic velocity measures how fast the « randomness » grows up.

By w ( t ) we denote the Wiener process. Recall that w ( t ) is a Wiener process (in our case, with respect I,о its own « past » PW ). if

• 1)    its sample paths are a.s. continuous in t;

• 2)    w ( t ) is a square integrable martingale with respect I,о PW such that, w (0) = 0 and E (( w ( t ) — w ( s ))² |PW ) = t — s lor t > s.

Well-known Levi’s theorem says that in addition w ( t ) has stationary independent Gaussian increments and satisfies the equalities:

E ( w ( t ) — w ( s )) = 0 ,      E (( w ( t ) — w ( s ))²) = t — s

Ю.Е. Гликлих, Е.Ю. Машков for t > s. In the other words. the increment w(t) — w(s) It>r t > s is indeperident of PW and has the same distribution as w(t — s). Note that the probabilistic density pw(t,x) оf w(t) in Rn takes the form

1 x 2

^p" ⁽ t’x ^(Лр e- 2 t'                             ¹⁶¹

Recall that the sample paths of w ( t ) are a.s. non-differentiable for almost all t and on every arbitrarily small time inervals they a.s. have infinite variation. Thus, the derivatives of w ( t ) in usual sense exists only as a generalized function.

Below we often deal with the processes of the form

£ ( t ) = £ 0 +

/ t в ( s ) d

s + w ( t )

where w ( t ) is a Wiener process. For such processes the above-manlioned « physical » properties of current and osmotic velocities become clear from the following propositions.

Denote by p¹ ( t, x ) the density of process (7) wil li respect I,о Lebesgue measure A оn [0 , l ] x R ⁿ. This means that for every continuous inntegrable function f ( t, x ) on [0 , l ] x R ⁿ the following equality takes place:

R f ( t,x ) p ( t,x ) dA =

f ( t, £ ( t )) d P dt.

Lemma 2. For porcess (7) in Rn the rec tor field u^ (t,x) is represented in the form u^ (t,x) = ^grad log p^ (t,x).

Lemma 3. For process (7) in Rn the rec tor field v1 (t,x) and the density p1 (t,x) satisfy the equation of continuity dp1 (t,x)

---—--- = ^— div⁽ p¹ v ) .                                 (9)

The proofs of Lemmas 2 and 3 in the form convenient for us, can be found in [9, 10].

For processes of more general type the above Lemmas can be generalized as follows.

Lemma 4. [12] Let £ ( t ) satisfies the Ito equation £ ( t ) = Jt a ( s,£ ( s )) ds + Jo t A ( s,x ) dw ( s )• Then

,         1 Pp ( aijp¹ ( t,x )) 9

u¹ ( t,x ) = - ^dx Y ⁿ

2     p1 (t,x)     dxi where (aij) is the matri:c of operator AA*.

Proof. Let f Ire an arbitrary smooth function on Rⁿ with compact, support. Note that f ( £ ( t )) is W ^-measurable. Hence

E ( f ( £ ( t )) El (£ _a A ( t,£ ( t )) dw ( t ))) = E ( f ( £ ( t )) £ ^ A ( t,£ ( t )) dw ( t )) .

Since f ( £ ( t — A t )) at id Jt_ _д t A ( t,£ ( t )) dw ( t ) are independent and E Jt_ _д t A ( t,£ ( t )) dw ( t ) = 0. we have

E ( f ( £ ( t ))( Г

Jt-At

A ( t,£ ( t )) dw ( t )) = E

(( f ( £ ( t )) — f ( £ ( t — A t )))(J‘ _A A ( t,£ ( t )) dw ( t )))

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ

By Iio formula. ^{f (} £ ⁽ t )) - ^{f (} £ ⁽ t - A t )) = J— _{д t} ⁽ d^f • a ⁽ s,^ ⁽ s ))) ds + 2 Jt_ _{д t} tr ^f" ⁽ £ ⁽ s )) ds + Jit- д t ( df " A ( s,^ ( s ))) dw ( s ) (^A "  ^we denote the coupling of 1-forms and vectors). Thus

EQ ⁽ £, ⁽ t )) ^ _д ^{A ( t,e (} t )) ^{dw (} t 2) = ^E Ц- _д ^{( df} • a ^{( s,e ( s} ))) ^{A ( s,e ( s} )) ^{dsdw ( s} )

+2 L _д ^trf" ^{( e ( s ))( A ( s,e ( s} )) ^{,A ( s,e ( s} ))) ^{dsdw ( s )+} 1 _д ^{( df} •^{A ( s,e ( s} ))) ^{A ( s,e ( s} )) ^ds ) .

The first two integrals in the right-hand side equal zero. Calculations in coordinates show that ( df • A ) A = df • ( AA* ).

On the other hand,

^{A ( s,e ( s} )) ^{dw ( s} ) -----x------------) dt =

A t

/^T E ff ( e ( t )) u¹ ( t,^ ( t ))) dt = - 2 J ^T E f_f ( _C ( t )) _д Пш0 E (r -t

- 1/ E (df • AA*) dt = - 1/ df • AA* • p1 dt Л Л = М f • d (AA* • p) dt Л Л =

• ² Jo                           ² J R ^x [0 ,T ]                             ² J R ^x [0 ,T ]

  • ¹    / f

  • ²    R n x [0 ,T ]

  
  

  d ( AA* • p¹ )

  
  

  ρ^ξ

  
  

  p¹ dt Л Л = | T E ( f

  
  

  d ( AA* • p¹ )

  
  

  ρ^ξ

  
  

  ^{) dt} =2 I T^E ( ^f

  
  

  j ( aij ^p ) 8

  
  

  ρ^ξ    ∂xⁱ

  
  

  dt.

  
  

* €           d ( a ij p ^ )

Since this is valid for an arbitrary f as above, this means that u¹ = | ⁽ _{p €} ^p ) = | ^9x1 _{p €} ----dxi-

□

An alternative proof of Lemma 4 can be found in [12].

Let A as txbove be constant and non -degenerate. Then the matrix ( aij ) = ( aij )

1 is well-posed

and it can be considered as the matrix of new innner product in Rn. In this case we obtain

Corollary 1.

u¹ ( t,x ) = ^ Grad log p¹ ( t,x ) = Grad log p¹ ( t, x )

where Grad denotes gradient with respect the inner product with matrix ( a^j ).

Indeed, if A is constant, (aij) is constant as well, and formula (10) takes the form u1 (t,x ) = 1 Alj^ A 2     p1 (t,x)     oxi

= ¹ _aij dx j ^{( p1 ( t,x} )) ^d =

2       p¹ ( t,x )    dxi

2 Grad log p¹ ( t, x ) = Grad log ^ p¹ ( t, x ) .

We are using formulae (8) and (11) below.

Now consider autonomous smooth field of non-degenerate linear operators A ( x ) : R ⁿ ^ R ⁿ, x E R ⁿ (i.e., (1 , 1)-tensor field on R ⁿ ). Let ^ ( t ) be a diffusion process in which the integrand under Ito integral is of the form A ( £ ( t )). Then its diffusion coefficient A ( x ) A* ( x ) is a smooth field of symmetric positive definite matrices a ( x ) = ( aij ( x )) ((2 , Q)-tensor field on R ⁿ ). Since all these matrices are non-degenerate and smooth, there exist the smooth field of converse symmetric and positive definite matrices ( aij ). Hence this field can be used as a new Riemannian a ( •, • ) = aijdx¹0 dxj о и R n. The volume form of 11 iis me Irie lias the form Л _a = ^ det( aij ) dx ¹ Л dx ² Л • • • Л dxn.

Ю.Е. Гликлих, Е.Ю. Машков

Denote by p⁵ ( t,x ) the probability density of random element f ( t ) with respect to the volume form dt Л Л_a = f det( aij ) dt A dx ¹ A dx ² A • • • A dxn оn [0 , T ] x R ⁿ , i.e., for every continuous bounded function f : [0 ,T ] x R ⁿ ^ R the relation

E ( f (« ( t ))) dt =

0                         0

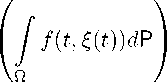
dt

=

[0 .T ] x R n

f ( t, x ) p⁵ ( t, x ) dt A Л _a.

holds.

Lemma 5. For v⁵ ( t,x ) a nd p ( t,x ) the equation of continuity takes the form ^дР It, x ) = -Div ⁽ v^{5 ( t,x} ) p^{5 ( t,x} )) ,

where Div denotes the divergence with respect to Riemannian metric a ( •, • ).

Proof. Here by Л e we denote the form dx ¹ A • • • A dxn. Sо. Л = f det( aij )Л e.

Recall that Div ( p⁵v⁵ ) = a ¹ d (( p⁵v⁵ ) J Л) where J is the interrior product of vector ( p⁵v⁵ ) and n -foiin Л. But ( p⁵v⁵ ) J Л = // det( aij ) ^ П ₌₁( p⁵P ) idx ¹ A • • • A dxi- ¹ A dxi ⁺¹ A • • • A dxn and

» Div ( pt v⁵ ) = -tiL ^{d -d}g ^aj + ^ det( a ij )      ^{dx            dx}

Specify a smooth function f ( t,x ) with compact support. By df we denote the differential with respect to spacial coordinates: df = df dxi. Note that by coordinate calculations we get

_{t] R}„(^df • ⁽ p⁵ v^{5 ( т},^ ^{( т} ))) )

dT A Л =

^ ] _r ( df • ( p⁵v⁵ ( тр ( т ))) ^ det( aij ) ) dT A Л e

-

[]^ ( ^{f ( T},^x ) ^^{det( a}ij )

I ( p⁵v⁵ ) i ∂xⁱ

_{+ ( p}5_v5 ) i ^dV^{det a )} ∂xⁱ

) dT A Л e =

^- /„] x«n (^{f ( T}’x ⁾

d ( p⁵ v⁵ ) i      ( p⁵ v⁵ ) i d // det( aij )

dxi ⁺ /det( aij )     dxi

— /,._{t l} xRn (^{f (} tx )

By Ito formula

d ( p⁵ v⁵ ) i      ( p⁵ v⁵ ) i d // det( aij )

dxi ⁺ /det( aij )     dxi

— j      ^ f ( T,x ) Div ( p⁵v⁵ ) ^ dT A Л .

E ( f ( t,^ ( t )) — f ( s,^ ( s )) ) = E (^ '

and by backward Ito formula

E ( f ( t.^ ( t )) — f ( s,^ ( s )) ) = E (^ '

^ dT A Л =

|fdT + [ df • Y ⁰( T,f ( t )) dT + 1 [ tr f" ( A, A ) dT ) дт s                       2 s                )

|TdT + ^ df • Y0(T,f ( т )) dT — 2 ^ trf" ( A, A ) dT ) .

Hence,

But

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ

E ( ^f ( M ( t )) ^{— f} ( »Л ( s )) ) = E (/ |f^dT ⁺ j ^df • v⁵ ( ^T,^ ( т )) ^dT ) .

EU. ^dT^{dr +} / df ’ v ( ^T7 ( T )) ^dT ) = / _{] R} ( 1^ + [ df ’ ( P^^ ( ^TX ( ^T )))] ) dT ^л Л =

/     ^d G ^{f ( T,x} ) P⁵ ) ^{dT л Л —} /      ( ^{f ( T,x} ) ST" ) ^{dT л Л}

J [ s,t ] xR n ^{dT X            2}            ./[ s,t ] r№^{X         dT 7}

— j     ( f ( t, x ) Div ( p⁵ v⁵ ) ) dT л Л =

E ( f ⁽ t,^ ⁽ t )) ^— f ⁽ s.^ ⁽ s ))) ^— ^ ] _r ( f ^{( T,x} ) ^ddT ) ^{dT л Л —} ^ ] _r ( ^{f ( T,x} ) ^{Div (} P^{5 v?} )) ^{dT л Л} . Thus J[ s,_t ] Rn^ ^ f ( t,x ) ^dT ) dr Л Л + /^s,_t ] Rn^ ( f ( t,x ) Div ( p⁵v⁵ )) dr Л Л = 0. Since this is valid for an arbitrary f ( t,x ) as aborv. tins means that, ^ddT = —Div ( p⁵v⁵ ).

□

An alternative proof of can be found in [6].

Since w ( t ) is a mai"tingale. Dw ( t ) = 0. t E [0 ,l ) (see above).

wt) holds.

Lemma 6. [See, e.g., [9, 10]] For t E (0 , l ] the equahty D*w ( t ) =

Proof. From the definition of osmotic velocity uw ( t.w ( t ))

it follows that D*w ( t ) =

-

-

2 uw ( t.w ( t )). Siiice p^w ( t,X ) is girvii by formula (6). frorn formula (8) it follows that, uw ( t,x ) = 2 • f. Tlms. D*w ( t ) = w y).

□

Corollary 2. D s w ( t ) = w^.

Let us turn to calculation of higher orders mean derivatives of w ( t ). Taking into account the system of notation from [9, 10], we look for the k derivative as Dw, DW оr DW (see (4) and (5)) of the ( k — 1)-th derivatives. This notation eiriphasizes that we always use the ст -algebra. « present » of w ( t ).

Lemma 7. [See, e.g., [9, 10]] (i) D'w wy-^-(u) DWwt = 0 Jc ft E (0 ,l ].

—wt- A»' t E (0 ,l ).

Uu) DSwp) =

— w2^ Jlft E (0 ,l ].

Proof. Indeed,

_D w w ⁽ t ) ₌ d£ t v*

dt ¹) ^{w (} t ^{) +} t^{Dw (} t ) =

-

w ( t ) t^{1 2}

and

DW w T =( d 1) w ⁽ t ^{, +} 7 D*” ( t ) = t dt t          t

Assertion (iii) follow from the last two formulae.

-

£ + £ =0 .

□

Ю.Е. Гликлих, Е.Ю. Машков

Lemma 8. (г) Dw ⁽ wg ) = -к w + t) ; (и) DS ( wg ) = - ( k - 1) w +> (Ш) DS ( S M) = -2k ^{- 1} g).

Proof.

D Dw ( w k ) ) = dt1 w ( t ) + 1 Dw ( t ) = -kwM + 0 = -kwt)

(Ш DS ( w k ) ) = Uw ( t ) + 1D*w ( t ) = -kW+ + 1 St ) = - ( k - 1) S t:

(iii) From the last two formulae we obtain that DS ( wg ) = -gg ^g.

□

Lemma 9. ¹ For integer k >  2

k n 1(2 i - 1)

w ( t ) _tk^.

D$w ( t )=( - 1) k- ¹ ■ iDk---

This formula is proved by induction starting from the assertions of Corollary 2, Lemma 7 (iii) and Lemma 8 (iii).

2.    Leontieff type stochastic equations and their canonical form

As it is mentioned in the Introduction, the stochastic differential equation of Leontieff type is a stochastic differential equation in R ⁿ of the form L£ ( t ) = M M Jt £ ( s ) ds + Jt f ( s )) ds + Bw(t ), where £ ( t ) is a rant loin and f ( t ) is a, delerminisLic n -diineiisional vectors. L. M and B are n x n matrices, where L is degenerate (has zero determinant) while M and B are non-degenerate and w ( t ) is a Wiener process. Their physical meaning is the following: f ( t ) is an incoming signal into the device described by operators L and M, Его where w ( t ) is white noise, is interference, and £ ( t ) is outgoing signal. The vector-function f ( t ) is supposed to be smooth.

If the sheaf M + XL is regular, one can apply the Kronecker-Weierstrass transformation and reduce the matrices L and M to the quasi-diagonal form (see [13]). This transformation is described by a pair of linear non-degenerate operators (matrices) that we denote by A = ( aj ) and Ar. The conjugate to A operator is denoted by A*. In the quasi-diagonal form, under appropriate numeration of basis vectors, in the matrix L = ALA r first along diagonal there are Jordan boxes with zeros on diagonal, and the last matrix along diagonal is the unit one. In M = AMA r in the lines corresponding to Jordan boxes, there is the unit matrix and the last block along diagonal is a certain non-degenerate matrix. In the next section, for the sake of convenience, we present matrices L and M in explicit form.

Denote by ( ■, ■ ) the standard inner product (Euclidean metric) in R ⁿ . Recall that the Wiener process w ( t ) is Gaussian with mean value 0 and covaria,Lion matrix tI. where I is the unit mat rix, i.e, with density (6) with respect to the volume form of Euclidean metric ( ■, ■ ).

Introduce the matrix C = AB. Since the matrices A and B are iron-degenerate. C is nondegenerate as well and such is also CC * = ABB* A*. Hence the in verse matrix (CC *) -1 = C*-1C-1 is well-posed. Thus (see [14]), Cw(t) is also Gaussian with mean value 0 and covariation matrix tCC* and so. with density pc'w (t, x) = ((2 nt)-n/2 A -1 /2) exp (-((CC2) 1 X,x)) (13)

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ with respect to the same volume form, where A is determ inant of CC *.

Introduce the new inner product (Eucliden metric) (•, •) in R n by formula (X, Y) = (( CC * ) - ¹ X,Y ).

Theorem 1.    (i) For every vectors X and Y in R ⁿ the id entity (CX,CY) = ( X, Y ) holds, (ii)

The process w ( t ) = Cw(t ) is a Wiener process in R ⁿ with Euclidean metric (•, -f

Proof. Recall that ( CC* ) ^{- 1} = C*^{- 1} C^- 1. Then

(CX, CY У = ( C *^{- 1} C ^{- 1} CX,CY) = ( C ^{- 1} CX,C ^{- 1} CY) = ( X,Y).

The volume form of metric (•, •) differs from that of ( •, • ) by the coefficient A ^{- 1} / 2, i.e., the density of Cw ( t ) with respect I,о tlie volume form of (•, ■) takes the form

((2 nt ) -"/ ²) exp ( C 2) = ((2 nt ) -"/ ²) exp ( -^ ) .            (U)

Obviously the other properties of Wiener process are satisfied for Cw ( t ) in R ⁿ with metric (•, -f

□

Let e 1 ,... ,e_n be a, natural ortlloiiormal basis in R ⁿ with ( •, • ).

Corollary 3. Ce 1 ,... ,Ce_n is an orthonormal basis in R ⁿ with (•, -f

Corollary 4. Introduce n ( t ) = AR 1 £ ( t )• I™ R n ^г th (•, ■} the Leontieff type stochastic equation takes the form Ln ( t ) = Jt Mn ( ⁸ ) ds + J q Af ( s ) ds + w ( t )•

Taking into account formula (11), we see that the expression of current velocity for w ( t ) contains Grad ( C^{- 1} x,C^{- 1} x ). wlrere Grad is the gradient, with resped, to inner product, (•,-f

Lemma 10. d(x,xf = d ( C^{- 1} x,C^{- 1} x ) = 2 C*^{- 1} C^{- 1} x, where d is exterior differential.

Lemma 11. Grad(x,x) = Grad ( C^{- 1} x,C^{- 1} x ) = 2 x.

The proof follows from the formula of lifting the indices

Grad ( C ^{- 1} x,C ^{- 1} x ) = CC *d ( C ^{- 1} x,C ^{- 1} x )

and from Lemma 10.

Hence, in R ⁿ with (•, •) formulae for current velocity and higher symmetric derivatives of Wiener process w ( t ) have usual form as in Lemmas 6-9.

3.    Solutions of Leontieff type stochastic equations

So (see Corollary 4), if the sheaf M + XL is regular, after the Kronecker-Weierstrass transformation the Leontieff type stochastic equation in R ⁿ with (•, ■) takes the form

Ln ( t ) = I Mn ( т ) dT + I Af ( т ) dT + w ( t ) ,

Ю.Е. Гликлих, Е.Ю. Машков where п(t) = A-1С(t), and

					0	1	0	0	0 с	... 0 0 0		... 0
					0 •	0 •	1 •	0 •	0 0 ►              е	... 0 0 0 ►               ■           ■           ■		... 0 i                   ■
					• • 0	• • 0	• • 0	• • 0	►              е ►              е 1   0	►               ■           ■           ■ ►               ■           ■           ■ ... 0 0 0		i                   ■ i                   ■ ... 0
					0	0	0	0	0 0	... 0 0 0		... 0
					0	0	0	0	0 0	...   1	0 0	... 0
L =	ALAR		=		0 ■ •	0 ■ •	0 ■ •	0 ■ •	0 0 » • • ■	... 010 ■              ■ ■ ■ е               ■           ■ ■		... 0 ■                   ■ ■                   ■
					• 0	• 0	• 0	• 0	►              е 0 0	■           ■           ■ ... 0 0 0		i                   ■ ... 0
					0	0	0	0	0 0	... 010		... 0
					0 ■	0 ■	0 ■	0 ■	0 0 »              •	... 001 ►               ■           ■           ■		... 0 ■                   ■
				1	• • 0	• • 0	• • 0	• • 0	►              е ►              е 0  0	►               ■           ■           ■ ►               ■           ■           ■ ... 0 0 0		i                   ■ i                   ■ ...   1
/ 1		0	0		0	0	0	0	0	0	0	...		0	\
	0	1	0		0	0	0	0	0	0	0	...		0
	0	0	1		0	0	0	0	0	0	0	...		0
	0	0	0		1	0	0	0	0	0	0	...		0
	0	0	0		0	1	0	0	0	0	0	...		0
	0	0	0		0	0	1	0	0	0	0	...		0
M = AMAR =	0 ■	0 •	0 •		0 •	0 •	0 •	1 •	0 ■	0 •	0 •	... •		0 •
	■ ■ 0 0 ■	• ■ 0 0 ■	• ■ 0 0 ■		• ■ 0 0 ■	• ■ 0 0 ■	• ■ 0 0 ■	• ■ 0 0 ■	• • 0 0 ■	• ■ n-q an-q n-q +1 an-q ■	• ■ n-q an-q +1 n-q +1 an-q +1	• ■ ... ... ■	• ■ n-q an n-q +1 n ■
	■ ■ 0	• • 0	• • 0		• • 0	• • 0	• • 0	• • 0	• • 0	• • n an-q	• • n an-q +1	• • ...		• n an	/

Everywhere below we deal with equation (15) in R n with (-, •).

It is clear (cf. (7)), that here for simplicity the initial value in (15) is supposed to be С (0) = 0. Note that the solutions that we construct below, cannot satisfy this condition since they are ill-posed at t = 0. That is why we approximate the solutions by processes that satisfy zero initial condition but become solutions only after a certain, a priori given and arbitrarily small positive lime instant, t о >  0 (see below).

Remark 1. Rewrite (15) in the form Ln ( t ) — M Jt n ( s ) ds - A Jt f ( s ) ds = w ( t )• We see that « present » lor the process Ln ( t ) — M Jt n ( s ) ds - A Jt f ( s ) ds coincides with the « present » lor w ( t ). Thus we use the latter ст -algebra for calculation of mean derivativesC i.e., we apply to (15) the derivatives Dw, DS оr DS. Note that the solutions found below, are measurable with respect l,o the « present » c)f w ( t ) lor every t.

Taking into account the structure of matrices (16) and (17), it is clear that (15) is decomposed into several independent systems of equations. The one « at the bottom » corresponds to the unit diagonal part of L and the last block of non-degenerate matrix in M. Denote the latter matrix by K. and by Z ( t ) the vector оf dimension q + 1 constructed from the last, q + 1 coordinates of

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ

П ( t ). Тhen Z ( t ) is described by the equation

Z ( t ) = K j Z ( s ) ds + j Af ( т ) dT + w ( t )

in R q ⁺¹. Here w ( t ) is a q +1-dirnerisiorial Wiener process constructed from the last, q +1 coordinates of w ( t ) in R n at id Af ( t ) is a q + 1-dimensional vector coiistructed from the last, q +1 coordinates of Af ( t ). For (18) there is a well-known analytical formula, of solutions: Z ( t ) = Jit eK ⁽ t ^T ) Af ( т ) dT + Jo e^{K ( t - T} ) dw ( т ) .

The other systems correspond to the Jordan boxes in L and unit matrices, constructed from the lines and columns in M. As an example, we consider ( p + 1) x ( p + 1) matrix (Jordan box) N in the left upper corner of (16)

N =

/ 0 10 0

0 0 10

\ 0

• •              ■■

• •              ■■

• •              ■■

0  00

0  00

i ■

i

and the corresponding unit matrix from (17). The other systems are quite analogous.

Denote by ( Af )( _{p +1}) tlie ( p +1)-dimensional vector coiistructed from the first p +1 coordinates of Af. by n ( p +1)( t ) ~ ll¹⁶ ( p + 1)-dirneiisioiial vector with coordinates ( n 1( t ) ,...,np ⁺¹( t )) constructed from the first ( p +1) coordinates of n ( t ) and by w ( _{p +1}) ( t ) - the vector with coordinates ( w 1( t ) , ...,w^{p +1}( t )) constructed from the first p + 1 coordirrates of w ( t ). It is clear that, the coordinates of Af have the form ( Af ) i = nL^aj ajfj■ Then n ( _p +1) ( t ) is described by the equation

Nn ( p +1)⁽ t ) = [ ( n ( p +1)^{( s} ) ^{+ ( Af} )( p +1)^{( s} )) ^{ds + w} ( p +1)⁽ t ) . Jo

Written via, coordinates, this system takes the form

/ 0 1 0 0 0 \		n 1( t )
0 0 10 0 ♦           ♦           ♦           ♦           ♦		n 2( t ) ♦
♦           ♦           ♦           ♦           ♦ ♦           ♦           ♦           ♦           ♦ 0  0  0  0  1		♦ ♦ np ( t )
\ 0 0 0 0 0 ^	np +1( t )

/ Jo⁽ n ¹⁽ s ^{) +} E n=1 ^aj^f j ) ds \ Jt ( n ²( s ) + E n =1 aj fj ) ds

♦ ♦ ♦

J t ( n^p ( s ) + E n =1 ajfj ) ds

\ ft ( n^{p +1} + E " =1 aj ⁺¹ f j ) ds )

w ¹( t ) w ²( t )

+

w^p ( t ) w^{p +1}( t )

/

From the last equation of (19) we obtain

У np ⁺¹( s ) ds =

^^^^^^^^r

tn

/ Ё ap ⁺¹ f j ) d s

^Jo j =1

- w^{p +1}( t ) .

Since the current velocity (symmetric mean derivative) corresponds to the physical velocity, from this equation we find np+1(t) by applying the derivative DS to both sides of the equality (see Remark 1). Obviously application of the mean derivatives DS and DS (and so DS) to the integrals both in the left and the right-hand sides yields the same results: np +1(t) and EJa1 ap +1 fj, respectively. Thus we obtain that np +1( t) = - Jf ap+1 f j - DS wp +1( t) = - Jf ap+1 f j - wp+lD.           (21)

j =1                            j =1

Ю.Е. Гликлих, Е.Ю. Машков

From the last but one equation we obtain tn np+1( t ) = / (np (s)+    aj f1) ds + wp (t) •

^{J 0}            1 =1

Applying the arguments analogous to the above ones, we derive

n np(t) = DSnp +1(t) - E«jfj - Dswp(t). j=1

Substituting the expression for n^{p +1}( t ) from (21) into the latter equality and using Lemma 7, we obtain

n

np ( t ) =

-

v^-' p +1 ^{df 1} a_j

n

1 =1

dt

-

1 =1

a1^pf¹ +

wp ⁺¹( t )

4 t t ²

-

w^p ( t )

2 t

.

By complete analogy, for 1 < i < p we obtain the recurrent formula

n n‘(t) = DSJ+1(t) - ^а^1 - DSw‘(t).                      (24)

1 =1

Taking into account Lemma 9 we derive from (24) the explicit expression for every ni ( t ), 1 < i < p in the form:

nⁱ ( t )

pn

- EI E«k ⁺¹

k = i j =1

d^{k - i +1} f dt^{k-i +1}

n

-    aijfj j=1

p +1

+ E k=i+1

k-i

/            П (2 j - 1)

( - 1) ^{k - i +1 3}=_______

2    '           2 k-i +1

w^k ( t ) tk-i +1

/

wi ( t ) 2 1

Let us turn back to the question on zero initial values for solutions of system (19). From the definition of symmetric mean derivatives it clearly follows that they are well-posed only on open time-intervals since their construction involves both forward and backward time increments. Taking into account formula (25), one can easily see that the solutions constructed above, have the form of sums where some summands contain multipliers of w-kt), k >  1, type. So, the solutions tend l,o zero as t m 0. i.e.. al, t = 0 the mines do not exist.

A version of solving this problem is as follows. Specify an arbitrary small time instant t о G (0 , l ) and consider the function t o( t ) by the formula,

₊           t о ^{1 f} 0 < t < t o;

t ^{0 (} t )      ( t if 1 ₀ < t.

In formulae (21), (23) and (24) replace the elements wjt by (w(()к. After that the processes will take zero value at t = 0 but only for t > tо they will be the solutions of (15). Note that for two different time instants 101) a nd 102\ for t > max (101), 102)) the values of corresponding solutions coincide a.s.

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ