Stochastic Leontieff type equations in terms of current velocities of the solution II

We understand the differential equations of Leontieff type as a special class of algebraic-differential systems in R ⁿ of the form

Lx( t) = Mx (t) + f (t), where x (t) at id f (t) at -e n-diniensional vectors. L and M are constant n x n matrices where L is degenerate and M is not degenerate. With the use of such equations in papers by A.L. Shestakov and G.A. Sviridyuk (see e.g. [1,2]) the dynamical distortion of signals in radio devises is described. In the papers by L.A. Vlasenko T. Sickenberger and R. Winkler A.G Rutkas, M.S. Filipkovskaya and others such equations arise in mathematical models of oscillations and electric nets.

For applications of the above mentioned models it is important to take into account noise in the right-hand side of the Leontieff type ecpiation, i.e., random perturbation of white noise type. Recall that the white noise is well-posed in the space of generalized functions. In papers [3-5] a new approach for investigation of Leontieff type equations with noise is suggested that replaces the white noise by Nelson’s symmetric mean derivative (current velocity, see e.g. [7-9]) of the Wiener process that allows one to avoid using the generalised functions. The current velocities are natural analogues of usual physical velocities of deterministic processes. In this paper we investigate the processes that are described by Leontieff type equations in terms of the current velocities of the solutions. In should be pointed out that in such setting the current velocities of Wiener process are not involved from the very beginning.

The Leontieff type differential equations in terms of current velocity of solution are introduced and investigated in [6] under the additional assumption that the pencil of constant matrices satisfies the so-called "rank-degree" condition. Here we deal with the systems that do not satisfy this condition.

For simplicity we consider ecpiations, their solutions and other objects on a finite time interval t E [0 , T ].

Everywhere in the text we use Einstein’s summation convention in repeated upper and lower index.

1.    Preliminaries on the Mean Derivatives

Consider a stochastic process £ ( t ) in R ⁿ, t E [0 , l ], given on a certain probability space (Q , F, P ) and su£(t) is L 1-random. variable for all t.

Every stochastic process £ ( t ) in R ⁿ, t E [0 , l ], determines three families of a -subalgebras of a -algeIrra F:

• (i)    the "past" P generated by pre-ini ages of Borel sets in R ⁿ by all mappings £ ( s ) : Q ^ R ⁿ for 0 < s < t:

• (ii)    the "future" Ft¹ generated by pre-images of Borel sets in R ⁿ by all nlappings £ ( s ) : Q ^ R ⁿ fc>r t < s < l:

(Ш) the "present" ("now") Nt generated by pre-images of Borel sets in R ⁿ by the mapping £ ( t )•.

All families are supposed to be complete, i.e., containing all sets of probability 0.

For convenience we denote the conditional expectation of £ ( t ) with respect to Nt¹ by E ( • ).

Ordinary ("unconditional") expectation is denoted by E.

Strictly speaking, almost surely (a.s.) the sample paths of £ ( t ) are not differentiable for almost all t . Thus its "classical" derivatives exist only in the sense of generalized functions. To avoid using the generalized functions, following Nelson (see, e.g., [7-9]) we give

Definition 1. (i) Forward mean derivative D£ ( t ) оf £ ( t ) at time t is an L 1-random variable о/ the form

D£ ( t ) = lim E_t¹ ( ^{£ (} t ^{+ A} t ) —^) ^{s v 7} д t^ +o ^tv        A t        ⁷

where the limit is supposed to exists in L 1 (Q , F, P) and A t ^ +0 means that A t tends to 0 and A t >  0.

(ii) Backward mean derivative D*£ ( t ) оf £ ( t ) a1t is an L 1-random variable

t₍^{£ (} t ) ^{— £ (} t ^{— A} t h

^D*^{£ (} t ’ = д ^ +о Et (------A t ------)

where the conditions and the notation are the same as in (i).

Note that mainly D£ ( t ) = D*£ ( t ), but if, say, £ ( t ) a.s. has smooth sample paths, these derivatives evidently coinside.

From the properties of conditional expectation (see [10]) it follows that D^ ( t ) and D*К ( t ) can be represented as compositions of К ( t ) and Borel measurable vector fields (regressions)

Y0(t,x)= lim E(К(t + At) ~ К(t) К(t)= x), v , 7   дt^+0 v        At

Y0(t,x )=       E ( t ( t l ~| ⁽ t~ T t ) |_€ ( t ) = x )                  _(:i)

on R n. This means that DК ( t) = Y0(t, К ( t )) ^ai fo D*К ( t) = Y* ^o( t,К ( t ))•

Definition 2. The derivative DS = 2 ( D + D* ) is called symmetric mean derivative. The derivative DA = 2 ( D — D* ) is called anti-symmetric mean derivative.

Consider the vector fields

v ^{( t,x} ) = 2^{( Y0(t,x ) + Y} °^{( t,x} ))

and

1 u ^{( t,x} ) = 2^{( Y 0( t,x} ) ~ ^Y*^{( )( t,x} )) •

Definition 3. v^ ( t ) = v^ ( t, К ( t )) = DS К ( t ) is called current velocity of К ( t );

U ( t ) = U ( t, К ( t )) = DAK ( t ) is called, osmo tic. velocity of К ( t ).

For stochastic processes the current velocity is a direct analogue of ordinary physical velocity of deterministic processes (see, e.g., [7-9,11]). The osmotic velocity measures how fast the "randomness" grows up.

Recall that Ito process is a process К(t) of the form tt

К ( t ) = К 0 +

j a ( s ) ds + У A ( s ) dw ( s ) ,

where a ( t ) is a preicess in R ⁿ whose sample paths a.s. have bounded variation: A ( t ) is a, process in L (R ⁿ, R ⁿ ) such that for any element Aj ( t ) of inatrix A ( t ) the condition P ( ш| fT ( Aj )² dt <  to ) = 1 liolds: w ( t ) is a Wienei• process in R n the first integral is Lebesgue integral, the second one is Ito integral and all integrals are well-posed.

Definition 4. An Ito process К ( t ) is called a process of diffusion type fa ( t ) a nd A ( t ) are not anticipating with respect to pj and the Wiener process w ( t ) is adapted to P_t’. If a ( t ) = a ( t, К ( t )) aiul A ( t ) = A ( t, К ( t )). wh.arc a ( t,x ) aiul A ( t,x ) are Borel measurable, mappings from [0 , T ] x R ⁿ tо R ⁿ and to L (R ⁿ, R ⁿ ), respectively, the Ito process is called a diffusion process.

Below we are dealing with smooth fields of non-degenerate linear operators A(x) : Rn ^ Rn. x G Rn (i.e.. (1, 1)-tensor field on Rnf Let К(t) be a diffusion process in which the integrand under Ito integral is of the form A(К(t)). Then its diffusion coefficient A (x) A * (x) is a smooth field of symmetiic positive definite matrices a (x) = (aij (x)) ((2, 0)-tensor field on Rn). Since all these matrices are non-degenerate and smooth, there exist the smooth field of converse symmetric and positive definite matrices (aij). Hence this field can be used as a new Riemannian a(•. •) = ai-dx ® dx- оn Rn. The volume form of this metric has the form Лa =   det(aij)dx1 Л dx2 Л • • • Л dxn.

Remark 1. Below we deal with constant matrices A and a. Please note that in this case the field a ( •, • ) becomes a new Euclidean metric (inner product) on R n.

Denote by p⁵ ( t.x ) the probability density of random element e ( t ) with respect to the volume form dt Л Л _a = det( aij ) dt Л dx ¹ Л dx ² Л • • • Л dxn оn [0 , T ] x R ⁿ . i.e.. for every continuous bounded function f : [0 , T ] x R ⁿ ^ R the relation

T

T

j E ( f ( t.i ( t ))) dt = j I [ f ( W ( t )) d P

0Ω

dt

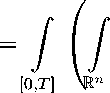
f ( t.x ) p⁵ ( t.x )Л a

dt

holds.

Lemma 1. [5,12] Let e ( t ) satisfy the Ito equation

Then

e ( t ) = e о +

f a ( s,e ( s )) ds + /

t

A ( s.e ( s )) dw ( s ) •

_x 1 j ^{( a}i^jP^{5 ( t,x} )) d u⁵ ( t. x ) = —

2     p⁵ ( t.x )      dxi

where ( aij ) is the matri.r of operator AA*.

Corollary 1. If A (and so also the matrix ( aij) is constant and non-degenerate,

1 . ,8                d 1

u = 2 aj gx- log p⁵ ( tx ) — = 2 Grad log p⁵ ( tx )

where Grad is the. gradient with respect to the. inner product a ( •, • ).

Note that (5) is valid in the case where A and so ( aij ) may be de generate. If A and so ( aij ) are not degenerate, the following proposition takes place.

Lemma 2. [9,11]] Let the matrices ( aij ) be non-degenerate. Vorix ( t.x ) a nd p ( t.x ) the following interrelation

^dp d t’ x ) = —Div ( v⁵ ( t.x ) p⁵ ( t.x ))

(known as the equation of continuity) takes place where Div denotes the divergence with respect to Riemannian metric a ( •. • ).

Following [11,13] we introduce the differential operator D2 that differentiates an L 1 random process e ( t )- t ^ [0 . T ] according to the rule

D  ( t ) =  i_im E5 (^{( e (} t ⁺ At ) ^—< ⁽ t ⁾⁾⁽ < ⁽ t ₊ At ) ^-< ⁽ t)У ) .

^2SV ’    △ t^ +o ^tv                   At                   ’

where ( e ( t + At ) — e ( t )) is considered as a cohrmii vector (vector in R ⁿ ). ( e ( t + At ) — e ( t )) * is a row vector (transposed, or conjugate vector) and the limit is supposed to exists in

L 1(0 , F, P). We emphasize that the matrix product of a column on the left and a row on the right is a matrix so that D2£ ( t ) is a symmetric positive semi-definite matrix function on [0 , T ] x R n. We call D2 the quadratic mean derivative.

Theorem 1. [11, 13] For an Ito diffusion type process £ ( t ) as (4) the forward mean derivative D£ ( t ) exists ат id equals Et ( a ( t )). In particular. if £ ( t ) a diffusion process. D£ ( t ) = a ( t,£ ( t )).

Theorem 2. [11,13] Let £ ( t ) be a diffusion type process as (4). Then D2£ ( t ) = Et [ a ( t )] where a ( t ) = AA* is the. diffusion coejfic-lent. In particular, if £ ( t ) is a diffusion process. D2£ ( t ) = a ( t,£ ( t )) where. a = AA* is the. diffu,sion coefficient.

Theorem3. [11,13] Let a ( t,x ) be a jointly continuous (measurable, smooth) mapping from [0 , T ] x R „ tо S₊( n ) (i.e., those matrices are non-degenerate). Then there exists a jointly continuous (measurable, smooth, respectively) mapping A ( t, x ) from [0 , T ] x R „ to L (R „, R „ ) such Un.it for all t E R. x E R „ the equality A ( t,x ) A* ( t, x ) = a ( t, x ) holds.

2.    The Main Result

We start this section with a glossary of some facts from matrix theory. Detailed explanation of this material can be found, e.g., in [14,15].

Definition 5. Let two n x n constant matrices A and B be given. The expression XA + B where X is a real or complex valued parameter, is called the matrix pencil. The polynomial det( XA + B ) (with respect to X) is called the characteristic polynomial of the pencil. If det ( XA + B ) is not identical zero, the pencil is called regular.

Theorem 4. Let the matrix pencil XA + B be regular. Then there exist non-degenerate matrices P and Q such that

^P ( ^{XA + B} >  Q = ^X(o ^) + ( J •               ¹⁹¹

where Id атid. I„-d are. unit matrices of the corresponding dimensions. N is an upper triangle matrix consisting of Jordan boxes with zeros on diagonal and J is a certain d x d block.

Let L be a degenerate n x n matrix and M be a non-degenerate n x n matrix such that the pencil XL + M is regular. Introduce a certain symmetric positive semi-definite n x n matrix 0 and consider the matrix 0 = Q 0 Q*. Evidently 0 is symmetric and positive semi-definite.

For C^ -smooth vector-function f ( t ) we consider the system

( LDs £ ( t ) = M£ ( t ) + f ( t )

I D 2 £ ( t ) = 0

that we call the stochastic Leontieff type equation with current velocities.

Take matrices P arid Q from Theorem 4 and construct matrices L = PLQ and M = PMQ. From formula (9) it follows that

^L (o n) ^alld M ( 0 I„_-d ) ■                   ⁽¹¹⁾

Note that since M is non-degenerate, J is also non-degenerate.

Consider n ( t ) = Q 1 € ( t ) ^and f ( t ) = Pf ( t )• Then according to the transformation of equation (10), explained in Theorem 4, we obtain the first line in (10) in the form LDSn ( t ) = Mn ( t ) + f ( t )• Siiice n ( t ) = Q- ¹ € ( t )• Roni the definition of 0 and definition of D2 by formula, (8) we get that the second line of (10) for n ( t ) takes tlie form D2n ( t ) = 0. Thus, equation (10) is transformed into the equation for n ( t ) in the form

Г LD s n ( t ) = Mn ( t ) + f ( t ) [ D 2 n ( t ) = 0 .

Thus, taking into account formula (11), one can easily see that the first equation in (12) splits into two independent equations: D_Sn ₁ ( t ) = Jn 1 ( t ) + f ₁ ( t ) and NDSn 2( t ) = n 2( t )+ f 2( t ) where n i( t ) aiid f ₁( t ) are constructet.1 from the first d coordinates of vectors n ( t )

and f ( t ). respect!vely. and n 2( t ) arid f ₂( t ) are constructet.1 from the last n — d coordinates

of n ( t ) arid f ( t ). respectively. Tins means that (12) might be solvable only if the matrix 0

takes the form

(

α 1

)

where a 1 = ( ai ) is a symmetric positive semi-definite d x d

matrix and a2 = ( ai ) is a symmetric positive semi-definite ( n — d ) x ( n — d ) matrix.

Hence (12) splits into two independent systems:

( ds n i⁽ t ) = Jn i⁽ t ^{) + f} i⁽ t ) D 2 n 1 ( t ) = a 1

and f NDsn2(t) = n2(t) + f2 (t) D2n1(t) = a2.

Let us first consider (13). Suppose that the matrix a 1 is non-degenerate (i.e., positive definite). For convenience we denote C^ -smooth vector field Jx + f (₁)( t ) in R ^d bу v ( t, x ) and denote its flow by g_t. Consider a probability density p ₀ in R ^d such that it nowhere equals zero. In this case it follows from [16, Theorem 3] that the density p ( t ) of the solution to (13) with initial density p ₀ takes the form p ( t ) = e^{p (} t ) where p ( t, x ) = p ₀( g_-t ( x )) — J ₀( Div v )( s,gs ( g_-t ( x )) ds, p ₀ = In p ₀. Here Div denotes the divergence with respect to inner product a ₁( •, • ) (see Remark 1). Note that p ( t, x ) is well-posed for all t G [0 ,T ]. By the construction v is the current velocity of n ₁( t ). Since the quadratic mean derivative is given as a 1 and we have foi.uid the density p. we can also find the osmotic velocity u by formula (6) and so the forward mean derivative a = v + u . Since a 1 is non-degenerate, by Theorem 3 there exists a matrix A such that a 1 = AA*. Then n 1 must satisfy the following stochastyic differential equation in Ito form:

n 1 ( t ) = n 1 (0) + I a ( s,n 1 ( s )) ds + j A ( s,n i ( s )) dw ( s )                (15)

in R ^d where n ₁(0) is the random variable with density p ₀. Equation (15) evidently has a strong and strongly unique solution well-posed on the entire interval [0 , T ]. .

Now let us turn to (14). Consider this equation on the example of (p + 1) x (p + 1) Jordan box in the upper left corner of N. In coordinates, equation (14) in this blok has the form:

•

«

« «

1 ... 0

I                                       I

I                                       I в . . . •

0 ... 1

0 ... 0/

DS

_n d +1_{( t ) n} d + _{( t )}

nd ⁺ p ( t )

_n d + p +1_{( t )}

( nd ⁺¹( t ) + / 2¹⁺¹ \ nd ⁺² ( t ) + / 2¹⁺²

nd ⁺ p ( t )+ /d ⁺ p

\n₂' ^{+ p +1}( t ) + /2 ^{+ p +}7

.

Thus nd ⁺ p ⁺¹ ( t ) =

^^^^^^^^^r

fd ⁺¹ and so

nd ⁺ p ⁺¹( t ) is n°t

random. Note that for non-random

processes DS coincides with f^. Then from the last but one line in (16) we see that

d + p          dn dd ^{+ p +1} ( t )

ⁿ 2   ⁽ t ) = ft

^^^^^^^^^r

t f + p / ₂

dfdd ⁺ p ⁺¹ ( t ) dt

^^^^^^^^^r

/d ⁺ p and so nd ⁺ p ( t ) is ⁿ°t random either.

Analogous arguments show that all other coordinates of n₂(t ) in (16) are not random. Note that (14) splits into independent equations corresponding to the Jordan boxes in N and for all those equations the above arguments are valid. Hence the process n₂(t ) is not random. But for any non-random process its quadratic derivative is equal to zero. So, (14) is solvable only if a ₂ = 0.

Note in addition that since n ₂( t ) is non-random, the "present" a -algebra for n ( t ) coincides with that for n ₁( t )•

Thus we have proved the following statement:

Theorem 5. Let L and M be degenerate (rankL = d) and non-degenerate, respectively, n x n-matnees. such that the. pencil XL + M is regular: let P an Q be n x n matrices that transform the. pencil XL + M into canonical form with L = PLQ and M = PMQ: let a 1 be a symmetric, positive definite, d x d matrix а/nd n x n ma trine 0 have the form 0 = a1 0

0 0

Then for every finite interval [0, T] and for every CMmooth n-dimensional vector-function /(t) equation (12) will 1, initial conditions n2(0) = x0 In Rn -d anul n 1(0) equal to a random variable with density p0 nowhere equal to zero in Rd, has a solution that is well-posed on the entire interval [0,T].

If n ( t ) is the. above-mentioned solution of (12). the. process f ( t ) = Qn ( t ) is a solution of (10).

Acknowledgements. The research is supported by Russian Science Foundation (RSF) Grant 14-21-00066, being carried out in Voronezh State University.