Стохастическая модель разделения зарядов в фотовозбужденных молекулярных триадах

DOI:

В последние несколько десятилетий все больше внимания уделяется исследованию детальных механизмов фотоиндуцированных реакций переноса электрона в супрамолекуляр- ных системах [2; 5–10; 14–17]. Примерами таких систем являются фотосинтезирующий реакционный центр, в котором под воздействием света происходит последовательный перенос электрона по цепочке вторичных акцепторов от хлорофилла-донора до вторичного хинона [6; 8], а также искусственно синтезированные донорно-акцепторные триады, включающие в качестве донора молекулу цинк-порфирина и два акцептора, ковалентно связанных с ней и находящихся на противоположных сторонах порфиринового кольца [10; 17]. В таких системах можно управлять фотоиндуцированным переносом электрона между отдельными компонентами, варьируя, например, длину волны фотовозбуждения и заселяя либо первое, либо второе электронно-возбужденное состояние. На основе таких молекулярных систем в настоящее время разрабатываются оптоэлектронные молекулярные переключатели типа «оn1-on2-off» [10; 17].

Детальное всестороннее исследование таких молекулярных систем имеет принципиальное значение для понимания механизма разделения зарядов на молекулярном уровне. Актуальным представляется исследование быстропротекающего неравновесного переноса заряда в донорноакцепторных триадах, индуцируемого светом и протекающего по схеме:

D A 1 A 2 ——— D * A 1 A 2 —— D + A ^- A 2 — >  D + A 1 A - .                 (1)

В рамках данной работы, используя хорошо апробированный стохастический подход [1–5; 7–16], выполнен аналитический расчет вероятности горячего переноса электрона с первичного акцептора на вторичный. Сделаны количественные оценки влияния распада продуктов на вероятность данного процесса и показано, что распад конечных ( D + A i A - ) и промежуточных ( D + A ^- А ^ ) продуктов реакции может заметно повлиять на вероятность разделения зарядов в триаде на неравновесной стадии.

Модель

Для количественного описания динамики двухстадийного разделения зарядов (РЗ) в электронно-возбужденных донорно-акцепторных триадах ограничимся рассмотрением трех состояний: электронно-возбужденного состояния донорно-акцепторной триады D ^* A ₁ A ₂, образующегося вследствие фотовозбуждения донора (реагенты), и двух состояний продуктов, промежуточного и конечного, заселяемых вследствие первичного и вторичного разделения зарядов (стадии I и II и на рис. 1А). Далее для дебаевских растворителей будет исследована динамика переноса заряда на вторичной стадии D + A ^- A 2 ——• D + A i A - с учетом их возможного распада.

Свободные энергии Гиббса U _а ( Q ) для рассматриваемых состояний триады выбираются в виде (рис. 1) [4; 5; 7]:

U 1 = ( Q - Q mu ) 2 /2 + А С 1₂ , U 2 = Q 72 , U 3 = ( Q - Q i« ) 2/ 2 + А G ,3 .         (2)

Здесь O minn = ^ 2 E^ , Q miin = ^2 E¹^ , E rr '¹, Б Г^и) - энергии реорганизации на первичной и вторичной стадиях разделения зарядов (см. рис. 1А). Параметры Δ G ₁₂ и Δ G ₂₃ определяют движущие силы реакции переноса электрона для этих стадий (рис. 1). Релаксационные свойства растворителя в рамках модели Дебая описываются автокорреляционной функцией K ( t ) [18], которая может быть измерена экспериментально:

^{K (} t ) = exP (^- t /Т L ),                                        (3)

где τ _L – время продольной релаксации среды.

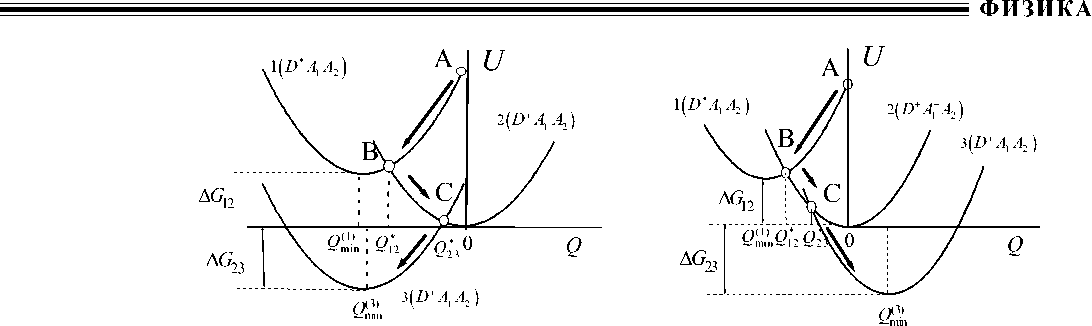
А

Б

Рис. 1. Схематическое изображение профилей поверхностей свободной энергии вдоль координаты реакции Q для электронных состояний триады ( D * A 1 A 2 ), ( D ⁺ A - A 2 ) и ( D ⁺ A 1 A 2 ).

Релаксация среды схематично показана стрелками. Вторичная стадия РЗ протекает в нормальной (панель А) и инвертированной (панель Б) областях Маркуса

Вероятность разделения зарядов в триаде на горячей стадии

В рамках стохастического подхода в квазистационарном случае с учетом распада промежуточного (τ _{V 1}) и конечного (τ _{V 2}) состояний продуктов в одноэкспоненциальном приближении релаксации среды (3) динамика электронных переходов в триаде описывается системой уравнений для функций распределения вероятностей электронно-колебательных состояний реагентов ( a = 1) и продуктов ( a = 2, 3) p _a ( Q , t ) [2-4; 11; 13]:

.f 8 ( Q - Q ,) + -^ P -P 1 ) 8 ( Q - Q *, ) + L P= 0 ,

• -    2 П т 2 ( й-P 1 ) ⁸ ( Q - Q 1*2 ) - ^( P-Р з ) 8 ( Q - Q -з ) + L - p - -^ = 0,        (4)

• -    2^ ( P-P 3 ) 8 ( Q - Q -з ) + L 3 P 3 "Г³- = 0.

• 11                                               1 ^ 3

Здесь V 12 , V 23 - матричные элементы электронных переходов 1 ^ 2 и 2 ^ 3, локализованных в точках пересечения термов Q ₁ ^* ₂ и Q ₁ ^* ₂ (рис. 1) соответственно. Следует отметить, что в рамках этой модели процесс фотовозбуждения явно не рассматривается, а считается, что триада в результате фотовозбуждения уже перешла в возбужденное состояние D ^* A ₁ A ₂ (состояние 1). В уравнениях (3) это описывается 8 -образным источником, локализованным в точке A c координатой Q , и имеющим мощность f .

Для расчета вероятности двухстадийного разделения зарядов будем использовать приближение, основанное на линеаризации термов в окрестности их пересечения. В этом случае операторы диффузии L _a ( a = 1, 2, 3) имеют вид: L _a = B d ²/ d Q ² + A _ad / d Q , где параметры A _a , определяющие наклоны касательных к термам в точках их пересечения Q ₁ ^* ₂ и Q ₂ ^* ₃ , равны средним значениям скорости движения частиц в окрестности этих точек. Параметр B = k _B T т^-1 связан с коэффициентом диффузии частиц по параболическим термам U _a ; T - температура; k_B - постоянная Больцмана; 1 — постоянная Планка. Распад промежуточных и конечных продуктов на временах τ _{V 1} и τ _{V 2} может быть вызван, например, процессами релаксации высокочастотных внутримолекулярных колебательных мод триады [9; 10; 12; 13], активных на данных стадиях.

Применяя Фурье-преобразование

P a ( Q ) = +f R a ( k ) e dk , a = 1,2,3,                               (5)

-« систему дифференциальных уравнений (4) сводим к системе алгебраических:

2*

f_ - ^- ike 0 ₊ _ i2 ( p ₂( q ) - _A( q )) e- i ^{( k +} i ^s )^Q _{+ ik}A i R — _k ² BR = o, 2 n h

• —% (P2 (Q*) -P1 (Q*))e-i(k+is)Q12* + k2 A2R2 - k2BR2 - -R- = 0,

h

2*

- Q ) -P 2 ( Q )) e" i ⁽ k ⁺ i ^{s ) Q 23} + k²A 3 R 3 - k²BR 33- = 0,

h решая которую, получаем:

_{R (} k ) = f    exp { - ikQ 0 }    ₊ _ V ^ex< i ( ^{k +} i ^{s) q} .2}

^Л    2n kB [ k - i ( A 1 / B ) ]    h     kB [ k - i ( A 1 / B ) ]

1 / 12 ^A P * _l ^ex p { i ( ^{k +} i ^s ) ^Q 2*1 }

R 2(k) = -U--------------------- h

- ,²₃ Ap *₂ exp { - i ( k + i s ) Q ₂ * ₃ }

kB ( k - iA 2 / B ) + 1] t _ ₂

_{R ( k} ) =- _ 3i ^A P 3*2^e xp { ^- i ( ^{k +} i ^s ) ^Q *3 } 3⁽ ) h kB ( k - iA 3 / B ) + 1 t _ ₃ ^.

Здесь используются следующие обозначения: Ap * =P 3 ( Q ₂*₃ ) -p ₂ ( Q ₂*₃ ) , AP 21 =p ₂( Q 1*₂ ) -p ( Q 1*₂ ) .

Выполняя обратные преобразования Фурье, находим аналитические решения для функций распределения вероятностей всех рассматриваемых состояний

^{P (Q} ) = A

6 ( ^{Q - Q} 0^)e xp

[ I A 1| ( Q - Q o ) b

<

+ 6 ( Q o - Q ) -

^- WC^- 9 ( ^{Q - Q} *2 ) exp

W ₂₃

P 2 ( Q ) =

fW CS

^W 23 ^A 2

-

I A 1I ( Q - Q 12 )

B

6 ( ^{Q - Q} 1*2 ) ⁺ exp

fW CS A 2

^{R( Q} ) =l^ AW C 3

- -CS- o ( Q 12 - Q )

W ₂₃

-   (q в (^2

6 ( ^{Q - Q} 2*3 ) ⁺ exp

exp «

- Q ) ^e ( Q 12 - Q )

-

^; - V^{( Q} 23 - ^Q ) | ^{e ( Q} 23 - ^Q )

^;- 1 AB ( f _ 3 - 1 ) ( Q - Q *2 ) } ^e ( Q - Q *2 )

—

+

+ exp «

^;- 1 AB ( 1 + f _ 3 ) ( Q *2 - Q ) ^e ( Q 32 - Q ) ,

—

и аналитическое выражение для вероятности разделения зарядов в триаде, протекающего в неравновесном режиме [4]:

6 6               Стохастическая модель разделения зарядов в фотовозбужденных молекулярных триадах

W =       W 12 W 23 exp { - ( f v 2 — 1> G 2I/ k B T }

CS   1 - W 12 W 23 exp { - f V 2 |A G *21/ k B T } ( A i]\A.| f v 2 )*

Параметр A G *2 в формуле (11) определяет величину вертикального энергетического зазора между стоками B и C A G ^ = U 1 ( Q* 12 ) - U ₃ ( Q *₃ ) (см. рис. 1), а W ₁₂ и W 23 - это вероятности переходов на каждом из стоков, рассчитываемые по формулам [1; 4; 11; 13]

W 12 = 2 п v 2 / [ h A 1 (1 + g 12 ) ] , W 23 = 2 п V 23 / [ h| A2 1 f_v 2 (1 + g 23 ) ] .                 (12)

Здесь g ₁₂ и g ₂₃ – параметры неадиабатичности переходов [1, с. 9; 3, с. 1503; 4, р. 124]

g 12 =

2 n V 2    1 ,      1

h [| A  A 2I f v 2

2 n V 2I      1

h [| Al f_v 3

⁺ I A 2 I f v 2

зависящие не только от наклонов термов, но и от факторов, учитывающих распад продуктов f_{v a} = V 1 + 4 B / t _{v a} A a ( a = 2, 3). Следует заметить, что полученные соотношения (12) справедливы только для реакций переноса заряда с большими значениями энергии активации прямого и обрат- *2                          *        (1) 2                          *2

ного переходов на каждой стадии: Q 12 /2 >>  k_BT , ( Q₁₂ + Q min ) /2 >>  k_BT , Q ₂₃ /2 >> k_BT , ( Q *3 - Q >2 >> k_BT [1; 11; 13], что накладывает ряд ограничений на параметры модели. Так, для реакции (1), протекающей в нетермическом (неравновесном) режиме, должно выполняться условие: Q тП <  Q *₂ <  Q *₃ <  0. Нетрудно также показать, что формулы (12), (13) являются естественным обобщением результатов, полученных ранее [1; 11; 13], и преобразуются в хорошо известные выражения в пределах т _v 1 ^да , т _{v 2} ^да [11], когда распад продуктов отсутствует.

Аналитические выражения (11)–(13) позволяют количественно оценить масштаб влияния основных параметров модели (энергий реорганизации среды E_r ^(I) , E_r ^(II) , времени ее релаксации τ _L , параметров электронной связи V ₁₂, V ₂₃, времен распада продуктов τ _{V 1}, τ _{V 2}, движущих сил реакции Δ G ₁₂ и Δ G ₂₃) на процесс двухстадийного РЗ в донорно-акцепторной триаде после ее фотовозбуждения.

Обсуждение результатов

Численное исследование W_CS проводилось в рамках Дебаевской модели среды с временем релаксации τ _L = 1 пс при комнатных температурах k_BT = 0,025 эВ. Энергии реорганизации растворителя на каждой стадии во всех расчетах полагалась фиксированными E^ = Е^ = 1 эВ, что характерно для сильных полярных растворителей. Величина свободной энергии реакции для горячего перехода на первичной стадии Δ G ₁₂ варьировалась в диапазоне от 0 до 0,8 эВ, что гарантировало протекание этого процесса на неравновесной стадии (0 < A G ₁₂ <  Е⁽¹⁾). При выборе параметра A G 23 проверялось выполнение условия Q *₂ <  Q 2₃ <  0 , что также соответствует неравновесному электронному переходу на вторичной стадии РЗ. При этом рассматривались конфигурации термов, соответствующие протеканию вторичной стадии РЗ как в нормальной области (рис. 1Б), так и в инвертированной (рис. 1Б). Параметры электронной связи V ₁₂, V ₂₃ выбирались в диапазоне до 0,06 эВ.

Некоторые результаты численного исследования влияния свободной энергии реакции на 2-й стадии разделения зарядов (ΔG23) на вероятность переноса электрона на вторичный акцептор (WCS) показаны на рисунке 2. Как следует из этих результатов, распад конечного состояния молекулярной триады (на временах τV3 порядка 50 фс) увеличивает эту вероятность (из сравнения сплошных и пунктирных линий). Наиболее заметно влияние параметра τV3 на WCS проявляется в нормальной (|AG23| < Er) области Маркуса (достигает 30 %), а в инвертированной области (Er <|AG23| < 2Er) WCS изменяется слабо при вариации тv3. Механизм влияния тр3 достаточно прозрачен: распад конечного состояния сдерживает обратный реакционный поток, что приводит к увеличению скорости прямого процесса и, следовательно, к росту вероятности WCS. При данном анализе не учитывался распад промежуточных состояний триады, но нетрудно показать, что в пределе быстрого распада (тг2 ^ 0 фс) фактор f „ ^ да, поэтому дальнейшее разделение заря-т ^0 V 2                        22 2

дов блокируется W CS —V——> 0.

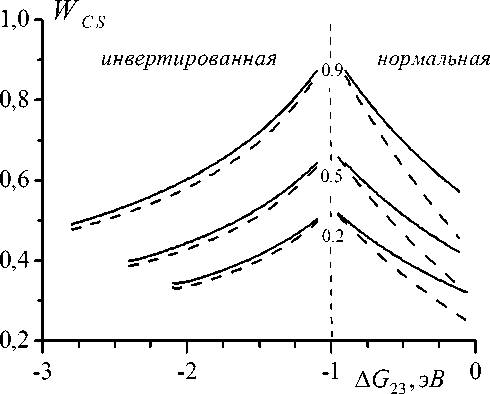
Рис. 2. Зависимость W_CS от параметра Δ G ₂₃. Варьируется Δ G ₁₂ (значения указаны возле кривых в эВ). Расчетные параметры: V ₁₂ = 0,02 эВ; V ₂₃ = 0,02 эВ;

τ _{V 3} = 50 фс (сплошные линии); τ _{V 3} = 10³ пс (пунктирные линии)

Для количественной оценки масштаба влияния распада конечного продукта τ _{V 3} на вероятность РЗ горячего перехода введем величину 8 W _C s , характеризующую относительное изменение данной вероятности при вариации времени распада продуктов в диапазоне от 50 фс до бесконечности:

• 5 W cs = ( W cs ( т V з ) - W_cs ( да ) ) / W_cs ( да ).

  
  

Как показало исследование, 5 W CS не зависит от движущей силы A G ₁₂ и параметра электронной связи V ₁₂ первичной стадии РЗ, поскольку вариация τ _{V 3} влияет только на вероятность переноса электрона на вторичный акцептор. Поэтому при анализе 5 W CS варьировались только параметры A G ₂₃ и V 23 . На рисунке 3 видно, что с ростом параметров электронной связи 5 W CS выходит на насыщение. Это обусловлено тем, что вероятность переноса электрона на вторичный акцептор W_CS перестает зависеть от V ₁₂, V ₂₃, когда реакция выходит на раствороконтролируемый режим.

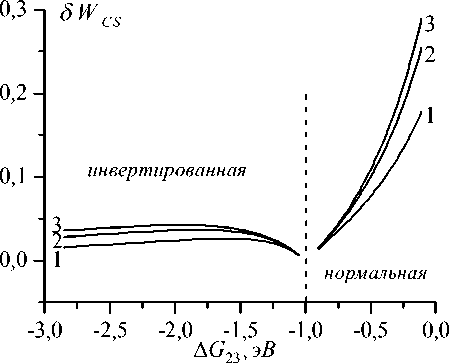
Рис. 3. Зависимость 5 W_CS от параметра A G ₂₃. Варьируются параметры электронной связи:

1 – V ₁₂ = V ₂₃ = 0,01 эВ; 2 – V ₁₂ = V ₂₃ = 0,02 эВ; 3 – V ₁₂ = V ₂₃ = 0,05 эВ. Параметр Δ G ₁₂ фиксирован: Δ G ₁₂ = 0,9 эВ

Рисунки 4 и 5 демонстрируют этот эффект насыщения при фиксированных значениях свободных энергий первичной и вторичной стадий разделения зарядов в триаде.

0,6

0,4

0,2

WCS

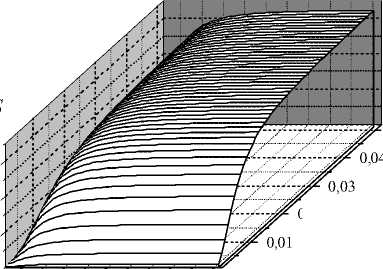
0,05

0,02 V ₂₃ , эВ

0,0 0,01 0,02 0,03 0,04 0,05

V ₁₂ , э в

Рис. 4. Зависимость вероятности РЗ W_CS от параметров электронной связи V ₁₂, V ₂₃. Расчетные параметры: Δ G ₁₂ = 0,8 эВ; Δ G ₂₃ = –1,5 эВ; τ _{V 3} = 50 фс

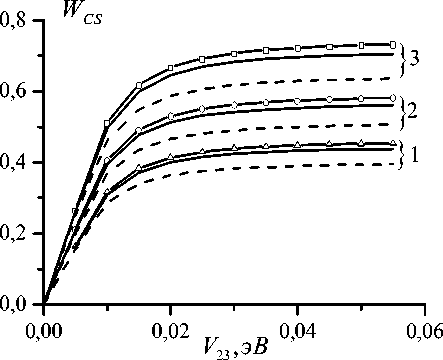
Рис. 5. Зависимость вероятности РЗ W_CS от параметра электронной связи V ₂₃.

Расчетные параметры: V ₁₂ = 0,02 эВ (серия 1); Δ G ₁₂ = 0,2 эВ (серия 2); Δ G ₁₂ = 0,5 эВ (серия 3); Δ G ₁₂ = 0,8 эВ; Δ G ₂₃ = –1,5 эВ; τ _{V 3} = 50 фс (сплошные линии); Δ G ₂₃ = –0,5 эВ; τ _{V 3} = 50 фс (символьные);

Δ G ₂₃ = –1,5 эВ; τ _{V 3} = 10³ пс (пунктирные)

Таким образом, показано, что ускорение реакции разделения зарядов в триаде, протекающей на неравновесной стадии, обусловлено распадом конечных продуктов, а ее торможение распадом промежуточных продуктов. Следует также подчеркнуть, что полученные выражения для вероятности разделения зарядов (11)–(13) можно обобщить на случай неэкспоненциальной релаксации среды, описываемой несколькими временами. Это позволит проанализировать зависимость W_CS от угла между направлениями координат реакции, соответствующих переносу электрона на первичный акцептор и с первичного акцептора на вторичный [5; 7].