Стохастическое описание смазки в искусственном и естественном тазобедренном суставе после ушиба

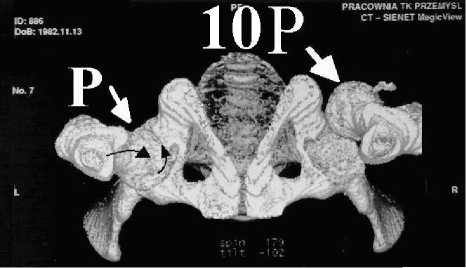
Данная статья посвящена численному анализу в области теории смазки поверхностей искусственного и естественного тазобедренного сустава при стохастических, нестационарных и импульсивных условиях. Статьи, приведенные в библиографии, не касаются проблемы смазки поверхностей искусственного тазобедренного сустава после ушиба при случайных условиях [1, 3, 4, 7–11, 19, 20]. Новые значения нагрузки тазобедренного сустава человека, происходящие в течение нескольких секунд после ушиба, очень часто решают вопрос о дальнейшем развитии вызванных этой травмой болезни или повреждения искусственного или естественного сустава. Поэтому для дальнейшей диагностики или терапии необходимо знание параметров смазки на основании случайных условий, например, изменения в течение нескольких микросекунд после травмы. Сосредоточенная сила P , приложенная к внешней поверхности кости, вызывает ушиб естественного тазобедренного сустава человека. Намного большая сосредоточенная сила P , приложенная к внешней стороне бедра человека, может повредить головку естественного сустава (см. рис. 1a) или искусственный сустав (см. рис. 1б).

а

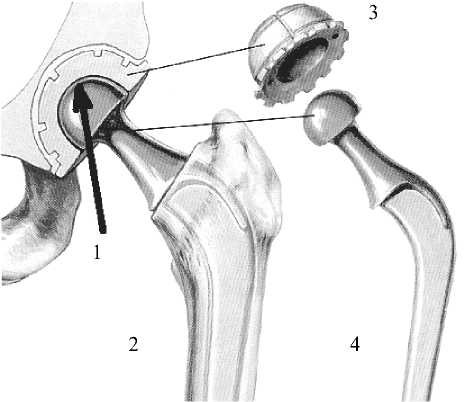
Рис. 1. a) Пренебрежимо малые изменения высоты щели, вызванные силой P , и большие деформации, вызванные силой 10 P , в естественном тазобедренном суставе человека; б) Искусственный тазобедренный сустав, нагруженный силой P : 1 – импульс силы, 2 – полный эндопротез тазобедренного сустава, установленный на месте, 3 – тазовый компонент (высокомолекулярный полиэтилен), 4 – бедренный компонент (металл)

• 2.    Определяющие уравнения и искажения высоты щели

Течение синовиальной жидкости в щели естественного тазобедренного сустава человека и течение биологической жидкости в щели искусственного сустава описывается уравнениями сохранения импульса и уравнением неразрывности. Эти уравнения вместе с приближением второго порядка общего определяющего соотношения Ривлина и Эриксена можно записать следующим образом:

div S = p —, div v = 0, S = - p I + ПоAi + « ( Aj ) 2 + P A₂ , dt                                   0 1         1           2

где S - тензор напряжений, p - давление, I - единичный тензор, A 1 и A ₂ - первые два тензора Ривлина-Эриксена, п , а , в - три материальные константы синовиальной жидкости, где п обозначает вязкость. Тензоры A 1 и A 2 даны в виде симметричных матриц, определенных в [12, 17]:

T                 d v

A1 = L + LT , A2 = grad a + (grad a) + 2LT L , a = Lv + —, где L - тензор градиента вектора скорости смазочной жидкости (в с-1), LT -транспонированный тензор, v - скорость (в м/с), t - время (в секундах), a - вектор ускорения (в м/с2).

Предполагается, что произведение чисел Деборы и Струхала, т.е. DeStr, и произведение числа Рейнольдса, безразмерного зазора и числа Струхала, т.е. ReyStr, имеют одинаковый порядок величины. Кроме того, DeStr >> Aа = аюп0, где ю -угловая скорость головки бедра. Мы предполагаем также вращательное движение головки бедра человека с окружной скоростью U = юR , где R - радиус головки бедра, несимметричное и неустановившееся течение синовиальной жидкости в щели, вязкоупругие и нестационарные свойства синовиальной жидкости, постоянную величину плотности синовиальной жидкости р, характерную величину высоты щели тазобедренного сустава 80 и условие прилипания на поверхностях кости [20-26]. Мы полагаем, что размерные и безразмерные величины связаны между собой следующими соотношениями:

r = 80r1, 9 = R91, t = t0ti, 8T = 808T1, vф = UvФ1, vr = U V vr 1, v9 = Uv91, p = p 0 Pi, p 0 = U^R ,(3)

( 8 0 )

а число Рейнольдса, модифицированное число Рейнольдса, числа Струхала и Деборы имеют вид:

Re =PU£0, Rev=pro(s0)2 , Str = A, De = ₽U,(4)

n              П 0           Ut 0

P^o)

DeStr =     , RevStr = V 0) .(5)

ⁿ 0 t 0                  ⁿ 0 t 0

Для синовиальной жидкости справедливо неравенство 0 <Р/ 1 _{0 0}, и псевдовязкость в в основном имеет значения от 0.0000001 до 0.001 Па^с². Безразмерные величины обозначены нижним индексом 1. Пренебрегая выражениями радиального зазора V = 8 ₀ / R ® 10^-3 и принимая во внимание вышеупомянутые предположения, получаем систему уравнений в сферических координатах ф , r , 9 [16,17]:

Re uStr — =— dp + — f—^ + DeStr ^v^,(6)

5 1 1       sin 9 1 5ф 5 r 1 ( 5 r 1 J         5 t 1 5 r 1 ²

0'p-(7)

d r 1

Re vStr ^VaL = -9pL + AfAl) + DeStr     ,(8)

5 1 ,        59 , 5 r I 5 r J          d t , 5 r ²

дVфL + sin (91 )dv7k +      V91sin (91 )] = 0,

5ф           5 r1   591LJ

0 <ф< 2 n0 1 , 0 <0 1 <  1, п/8 <9 1 <  л/2, 0 < r 1 T 1 , 8 T 1 - безразмерная высота щели. Символы v _{ф 1} , v r 1 , v 9 1 обозначают соответственно безразмерные компоненты скорости синовиальной жидкости в окружном, радиальном (по высоте щели) и меридиональном направлениях головки бедра.

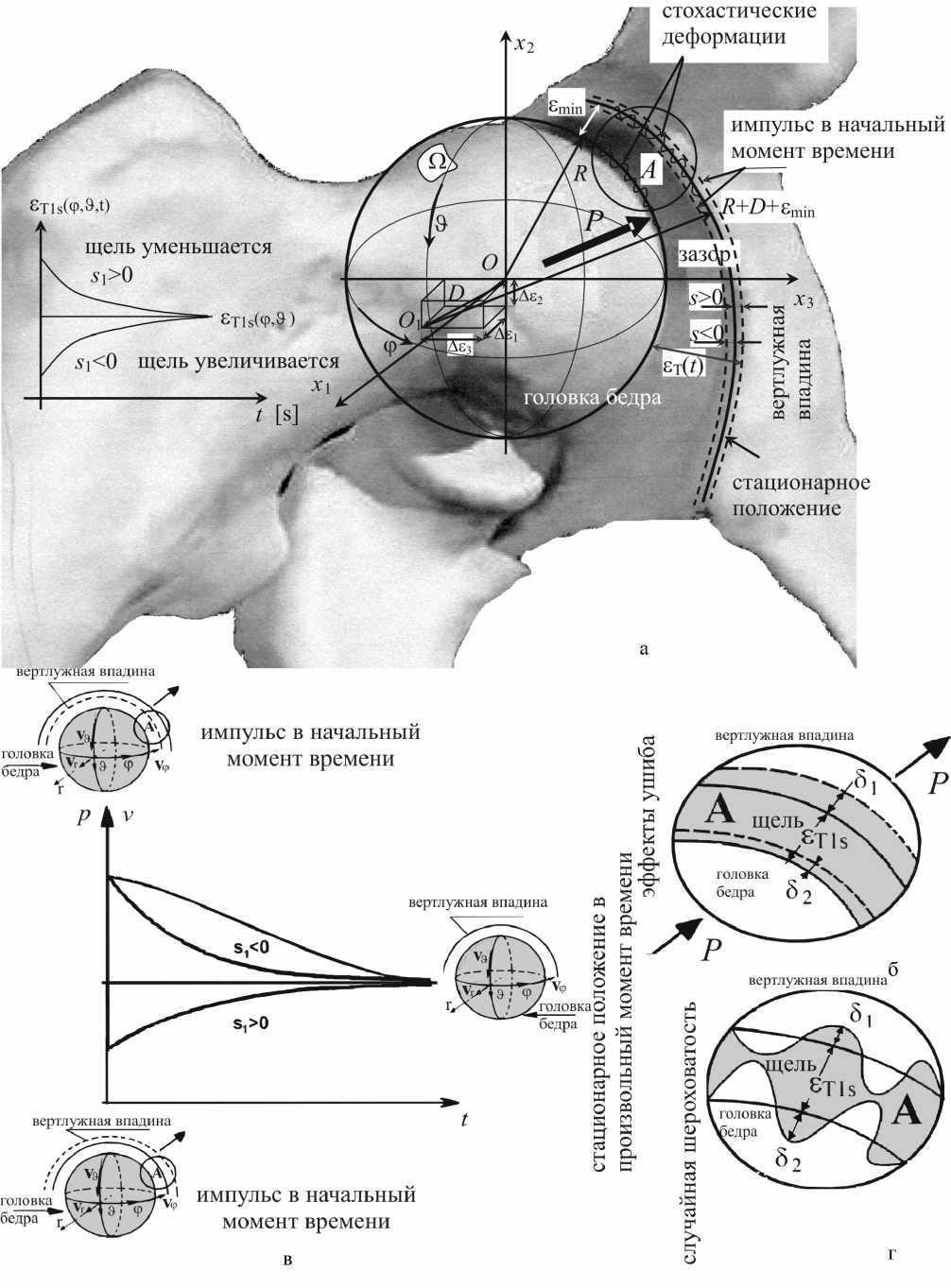
Рис. 2. a) Область смазки, эксцентриситеты, изменения высоты щели с течением времени после ушиба, б) положение в стационарном и импульсивном движении, в) графики зависимости от времени давления и скорости синовиальной жидкости, г) стохастические деформации, влияние ушиба, случайная шероховатость

Рис. 2a показывает изменения высоты щели сустава, вызванные импульсной нагрузкой при неустановившемся движении и стохастических эффектах [12, 17, 18]. Нестационарный импульс, который начинается в начальный момент времени, через некоторое время исчезает, и головка бедра или головка искусственного тазобедренного сустава возвращается в стационарное положение (см. рис. 2б).

Графики зависимости от времени скорости и давления представлены на рис. 2в. Рис. 2г показывает случайные эффекты шероховатости и волнистости, вызванные случайной фибрилляцией поверхностей хряща и склерозом субхондральной кости. В случае искусственного сустава мы имеем случайные эффекты шероховатости, вызванные следами от абразивных частиц. Безразмерная высота щели ел зависит от переменных ф , 9 и времени t и состоит из двух слагаемых [15, 26]:

8 T 1 = 8 т i s ( ф , 9 , t ) + 5 1 ( ф , 9 , ^ ),                                 (10)

где 8 _т 1 s обозначает полную безразмерную однородную часть геометрии тонкого слоя жидкости. Эта часть высоты щели содержит безразмерные поправки высоты щели, вызванные деформациями хряща. Символ 5 1 обозначает безразмерную случайную часть изменений высоты щели, возникающую в результате нестационарного нагружения неровностей поверхности хряща, измеряемую от номинального среднего уровня (см. рис. 2б). Символ ^ описывает случайную величину, характеризующую расположение неровностей. Оператор ожидания определяется выражением:

+∞

E (*) = ] (*) х f 1 ( 5 1 ) d 5 1 ,                                (11)

-∞ где f1 - безразмерная функция плотности вероятности.

• 3.    Поверхности головки и описание случайности

Реальное описание изменений высоты щели в естественном и искусственном суставе зависит от вариаций поверхностей хряща и от следов абразивных частиц. Случайные изменения поверхности хряща и поверхностей искусственного сустава описываются функциями плотности вероятности на основе сравнения между экспериментами автора и исследованиями Доусона [1], Моу [11] и Вежхольского [25] (см. рис. 3 и 4).

Изменения поверхностей образцов эндопротезов искусственного тазобедренного сустава проведены с помощью лазерно-механического сенсора. Измеряемые образцы были изготовлены из металла, циркония и алюминиевой керамики (см. рис. 3a, 3б). При измерениях использовались образцы из металла или циркония длиной 1.25 мм и шириной 1,25 мм, или даже длиной 2,50 мм и шириной 2,50 мм. Образцы, изготовленные из алюминиевой керамики, имели длину 0,988 мм и ширину 0,988 мм.

В случае искусственного эндопротеза Веллера металлическая поверхность головки покрыта хаотическими царапинами случайной формы, являющимися следами абразивных частиц [13].

Измеренные величины St для металлических головок эндопротеза Веллера едва составляли величину в 1 микрометр.

а

мкм

16,4 мкм

0,998 мм

0,998 мм

Рис. 3. a) Контурная диаграмма неэксплуатируемой поверхности металлической головки эндопротеза Веллера; б) Поверхность неэксплуатируемой головки эндопротеза из алюминиевой керамики

б

мкм

Измерения величины изменений на поверхности образцов (2 мм х 2 мм) нормального хряща, лежащего на сфере головки бедра естественного тазобедренного сустава человека, проведены с помощью механического сенсора в аппарате Rank-Taylor-Hobson-Talyscan-150 и обработаны с помощью компьютерных программ Talymap Expert и Microsoft Excel . Результаты приведены на рис. 4a и 4б.

Отсюда мы получаем следующую безразмерную функцию плотности вероятности [2, 14]:

/ 1 ( 5 1 ) ^

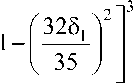
для |5 1| <+ 35/32 = 1,09375,

0 для |5 1| >  1,09375.

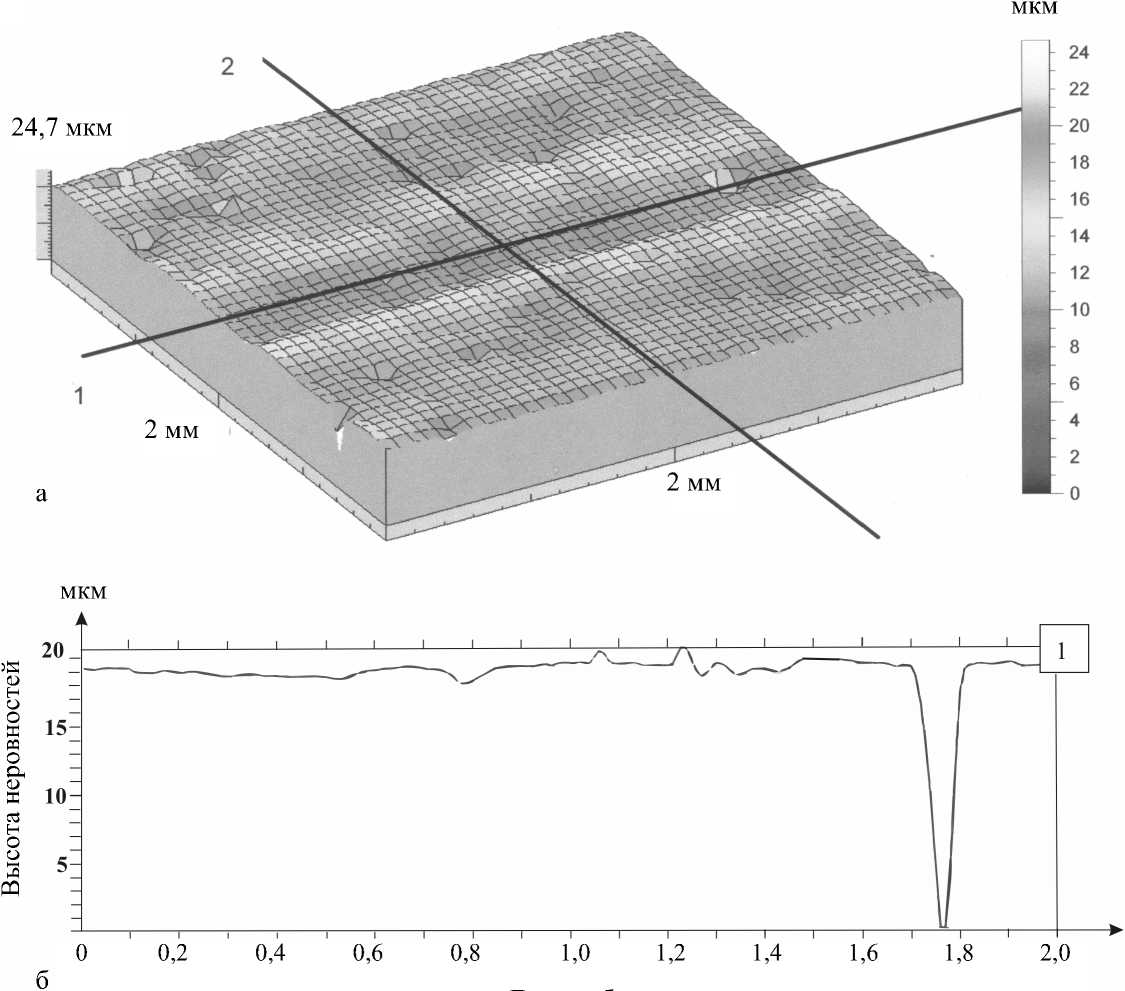
Длина образца

Рис. 4. а) Измерение шероховатости образца хряща (2мм х 2мм) из бедренной головки тазобедренного сустава человека; б) Неровности поверхности нормального хряща вдоль сечения 2-2 образца естественного хряща

• 4.    Интегрирование задачи гидродинамики для импульсивного движения

Введем новую безразмерную переменную [5, 6, 16]:

1 Re V Str X = Г 1 N , N = -

t ₁

DeStr

, t1 > 0,0 <------< 1, t1

и предположим решение системы (6)–(9) в виде следующих сходящихся рядов [3, 17]:

DeStr vФ1 = vФ02 (X, Ф, 91)+ —-— Vф12 (X, Ф, 91)+ t1

-eStr k t 1    7

v _Ф 2 2 ⁽ X , Ф , ⁹ 1 ) ⁺......... ,

DeStr v91 = vS0Z (X, Ф, 91) + —--- t1

V ₉ 1 2 ( x , Ф , ^ 1 ) +

DeStr k t 1    7

v 9 2 2 ( X , Ф , ⁹ 1 ) ⁺......... ,

DeStr vrl = vrO2 (X, Ф, 91) +-------vl2 (X, Ф, 91) +

t

DeStr v t 1 J

v r 2 2 ⁽ X , Ф , 9 1 ) +.........,

DeStr

P1 = Р10(Ф, 91, t1) + —---Р11(Ф, 91, t1) + t1

DeStr v t 1 J

Р 12⁽ Ф , 9 1 , t 1 ) +.........,

где t 1 >  0 , 0 <  DeStr <<  1, 0 <  DeStr/ 1 1 <  1 . Заменим в уравнениях (6)-(8) производные по переменным t 1 и r 1 производными только по одной переменной x , используя следующие зависимости:

e t

e

—^X = — 17Re у Str eX e t 1      4'

re)

r ₁    е х е

—

г e ex) ex Re у Str e

• 5    r 1 ²

^{e r} 1 v^{e r} 1 J

ex (ex 5 r 1 Je r 1

• ⁴    t 1 ex ²,

e Г Re у Str e ² '

е t 1 e r 1 ²     е t 1

—

•1 V ⁴ t 1

Re у Str г e ² + _vdx 2

4 t ₁ ²

^X J

X '

2 -У J

.

—

Re у Str д ²

4 t ₁ ²

дХ 2

+

Re у Str e

Ге2)

eX

• ⁴    t 1    ^eX^eX ² J^e t 1

После этого мы подставляем ряды (14)–(17) в измененную систему (6)–(9), где переменные t 1 и r 1 заменены переменной x • Кроме того, мы приравниваем выражения, умноженные на одинаковые степени параметра ( DeStr/ 1 1 ) k для k =0, 1, 2,... Таким образом, мы получаем следующую последовательность систем обыкновенных дифференциальных уравнений:

d ² v i 0 2 + _{2 x} ^d v 0 2 = ^{1 e} P 10 d X 2         ^d X     N i ^{2 ea} i ’

d ² v,_1y    , dv, .     1 e p,,    d ² v,_ny ,. 1 .

---i ^{1 2} + 2 x -^ + 4( v_{n y} ) =    -^1 + (1 + - X ), d X ²       d X            N 2 e« i    d X^{2 V} 2^

d v dv              1 e p     d v 1 d v

---if2 + 2x —i22 + 8(vi22 ) = —r -^2 + 2---i!2 + -X---i22, dX2       dX           Ni^ eai     dx2   2 dx

где i = ф , 9 ; а_ф = ф , а₉ = 9 1 и

( N ф ) 2 = N ² sin 9 1 , N ₉= N .

5. Стохастические уравнения Рейнольдса и среднеквадратичное отклонение

Сферическая головка бедра естественного сустава и головка искусственного сустава движутся только в окружном направлении ф . Поэтому компоненты скорости

синовиальной или биологической жидкости на поверхности головки в окружном направлении равны окружной скорости сферической поверхности головки бедра. Компонента скорости жидкости на сферической поверхности головки бедра в меридиональном направлении 9 равна нулю, так как сферическая головка не движется в направлении 9 . Вязкая синовиальная жидкость течет вокруг головки. Тогда на поверхности головки компонента скорости синовиальной жидкости в радиальном направлении (по высоте щели) равна нулю.

Таким образом, мы имеем следующие граничные условия:

v ф 0 ! ( X = ⁰⁾ = sin ⁹ 1 , v 9 0 ! ( X = ⁰⁾ = ⁰ , v r 0 ! ( X = ⁰⁾ = ⁰ ; для r 1 = 0 о х = 0 и 0 <  t 1 <  1 ₂ < да , N >  0.

Сферическая поверхность вертлужной впадины не движется в окружном и меридиональном направлениях, но совершает некоторые колебания в радиальном направлении (по высоте щели). Следовательно, высота щели изменяется с течением времени. Таким образом, компоненты скорости жидкости на поверхности вертлужной впадины в окружном и меридиональном направлениях равны нулю. Компонента скорости жидкости в радиальном направлении r (по высоте щели) равна первой производной по времени от высоты щели. Отсюда мы имеем следующие граничные условия:

d8„„ vф0! (X = M) = 0, v90! (X= M) = 0, vr 0! (X= M) = Str ^f1;

d t1

r 1 ^8 1 о x ^ N 8 _T 1 ^ M and 0 <  t 1 <  1 ₂ < да , N >  0,

где 8 _T = 8 0 8 _T 1 - высота щели, 8 _T 1 - безразмерная полная высота щели, Str ^ 1/ го 1 0 .

В силу граничных условий (23), (24) компоненты скорости синовиальной жидкости в направлениях ф и 9 для нестационарного течения имеют следующую безразмерную форму:

v ф 0 ! ⁽ Ф , ^r 1 , ⁹ 1 , t 1 ) = + ^{sin 9} 1 ^— 1 ^{sin 9}:

—

П ⁹ Р 10

¹ 2 N ² sin 9 1 5ф

Y ⁽ X = N ⁸ T 1 ) ^X

X

erf( r ₁ N )

п дРю

erf ( 8 1 N ) 2 N ² sin 9 1 5ф

Y ( X = N 1 ),

v 9 0 ! ( Ф , r 1 , ⁹ 1 , t 1 ) =

^{n d} Р 10

2 N ² 59 1

Y (x = N8 t 1 )X

erf( r 1 N )     Пк 5 p ₁₀

erf ( N 8 _T 1 ) 2 N ² 59 1

Y ( X = N 1 ),

где

X .2                             X .2

Y (x) = J eX1 erf X1 d X1 — erf xj eX1 d X1

1 Re w Str N =   ------,

2        t 1

2 ^Х 1 .2 erf ( X 1 ) = ^ J e  d X 2 ,

vn 0

и 0 < t 1 <да , 0 < r <8 T 1 , b m1 <9 1 < b s 1 , 0 <ф< 2 я6 _1? 0 <6 1 <да , 8 t 1 =8 t 1 ( ф , 9 1 , t ^, ⁰ < X 2 1 ^r 1 ^N <⁸ t 1 ^N = M .

Подставим компоненты скорости (25), (26) в уравнение неразрывности (9) и проинтегрируем обе части этого уравнения по переменной r ₁ . На поверхности головки бедра радиальная компонента скорости синовиальной жидкости v _{r 0 !} (в направлении высоты щели) равна нулю. Поэтому, подставляя граничное условие v _{r 0 !} = 0 для r 1 = 0, получаем компоненту скорости синовиальной жидкости в направлении высоты щели в следующем виде:

v r 0 ! ⁽ Ф , ^Г 1 , ⁹ 1 , t 1 )

Ne ‘²¹N¹ r Г ef r N ) dr erf( h 1 N ) ^J erf( s T 1 N ) ²

^ Я 1  '- -p +3^ p )  ' T1Ne z2erf d5ф 2 ^ sin2 91 5ф 5ф   591 591 J N J

—f-4-' p +^ + ^d p O cot 9

2 ^ sin² 9 1 5ф     59 2    59 1

1                      ^r;

J-2- Y ( x = h l ^N ) J

N            0

erf( r 1 N ) _dr erf( h ₁ N ) ¹

- J Y (Xi = r2N)

^dr2 *

где 0 <  t 1 <« , я/ 8 <9 1 <я/ 2, 0 <ф< 2 ^0 1 , 0 ₂ 1 r 1 N _T 1 N = M , 0 <0 1 <  1, 0 <  r <  r i < s t i .

Компонента скорости синовиальной жидкости в направлении высоты щели v _{r 0 !} не равна нулю на поверхности вертлужной впадины. Поэтому, интегрируя уравнение неразрывности (9) по переменной r ₁ , накладывая на компоненту скорости в направлении высоты щели граничное условие (24) при r 1 = s 1 и принимая во внимание условия (23) при r 1 = 0, получаем следующее уравнение:

1 5 ^s Т ¹ . , 1 5 ⁸ T ¹ . _n , _ 5s_n ——— I ^V ф 0 Z ^dr1 +—— — I sin ⁹ 1 v 9 0 ! ^dr1 = ^{- Str} "ГТ¹ sin 9 1 5ф 0 sin 9 1 59 1 0 5 1 1

.

Если подставить выражения (25)–(26) в (30) и взять ожидаемые величины обеих частей уравнения (30), мы получаем следующее модифицированное уравнение Рейнольдса:

vn   1

2 N ² sin 9 1

E ^

55ф

J ( s T 1 N ) - p ¹⁰

5ф

n+

2 N ²

E ^

J ^{( s} t 1 ^N ) I p psin ⁹ 1

—

(sin 91) E < — H(sT 1 N) * — Str [5ф

5 E(s_T J . _ — T  sin 9,,

5 1 1             ¹

где

⁸ T 1

J ( s _T 1 N ) ^ W ( s _T 1 N ) Y ( s _T 1 N ) — J Y ( r 1 N ) dr 1 , H ( s _T 1 N ) ^ s _T 1 — W ( s _T 1 N ),       (32)

^S T 1

j erf r 1 N ) dr 1

W ( s T 1 N ) -

erf( s T 1 N )

и s T 1 = s T 1 s ( ф , 9 1 , t 1 ) + 5 1, 0 < r ₂ <  r 1 T 1 , я/8 <9 1 <  л/2, 0 <ф< 2 я0 1 , 0 <0 1 <  1, 0 <  t 1 < да , 0 < x ₂ < X i <  s T i N , 0 <  N ( t 1 ) = 0.5^/ReStr/ t 1 < да .

Модифицированное уравнение Рейнольдса (31) определяет неизвестную функцию давления p₁₀ ( ф , 9 1 , t 1 ).

Используя функцию оптимума f 1 распределения плотности вероятности для стохастических изменений щели, вызванных шероховатостью и нестационарными изменениями (см. уравнение (10)), получаем, что математическое ожидание полной толщины слоя E ( s T 1 ) и математическое ожидание функции давления E ( p ₁₀) могут быть представлены с помощью оператора ожидания в следующей форме [26]:

+да

E ( * ) = J ( * ) ^х / i ( 5 i ) d 5 i , f , ( 5 i ) -

1 -

5| c1 )

для - c 1 <5 1 <+ c 1 ,

0 для |51| > c1, где символ c1=1,09375 обозначает половину полного диапазона случайной величины толщины тонкого слоя для нормального тазобедренного сустава. Безразмерное среднеквадратическое отклонение высоты щели (*), представленное уравнением (10), имеет вид:

• a ,    = V E ( . ) ² - E ²( . ) = -35- = 0,3645.                      (35)

32 • 3

Чтобы получить размерную величину среднеквадратического отклонения, нужно умножить безразмерное среднеквадратическое отклонение a1 на характерную величину высоты щели s0 .

В соответствии с экспериментальными величинами, относящимися к искусственному суставу, мы имеем размерное среднеквадратическое отклонение a 1 =1 мкм . Чтобы получить безразмерное среднеквадратическое отклонение a 1 =0,3645, мы должны предположить характерную величину высоты щели равной s ₀ =3 мкм.

Экспериментальные данные для естественного сустава дают размерное среднеквадратическое отклонение a 1 =3 мкм . Для того, чтобы получить безразмерное среднеквадратическое отклонение a 1 =0,3645, нам нужно предположить, что характерная высота щели составляет величину порядка s ₀ =10 мкм .

Принимая во внимание соотношение (34), мы можем переписать уравнение (31) в следующем виде:

л/л    1    5

2 N ² sin 3 1 do

И

- c l

1 -

I

cl )

J ( s t i N )

d op

5ф

H

V п d +

2 N ² 53 ₁

И

^- c l

1 -I

c1 )

J ( s t 1 N )

d 5, - p ¹⁰sin 3]

¹ 53 ₁       ¹

-

+ c 1 f     ^2

( sin 3 1 )^J 1 -^ H ( s T 1 N ) d 5 1 1 ^ф — ' ( c )

-

-

C1 ^

+ ^C 1 Л    e2 V^

Str— J 1 —T

⁹ t 1 - C 1    c 1 )

^(s T 1 s ⁺⁵ 1 ) d ⁵ 1

sin 3 ₁.

где - c ₁ < 5 ₁ <  c ₁, л/ 8 < 3 ₁ < л/ 2, 0 < ф <  2 п .

Зависящую от времени высоту щели с учетом возмущений и стохастических изменений можно записать как:

s T 1 = s T 1 s ( ф , 3 1 , t) + 5 1 = s T 1 s ( ф , 3 1 ) [ 1 + se ^- ‘ ⁰ ^ ]+5 1 .                (37)

Не зависящая от времени постоянная часть значения высоты щели в размерной форме имеет вид:

s ₀ s _{T 1 s} ( ф , 3 ₁) = s _Ts ( ф , 3 ₁) ^ As ₁ cos ф sin 3_t + As ₂ sin ф sin 3 + As ₃ cos 3_t - R + +^(A.£ ₁ cos ф sin 3 ₁ +As 2 sin ф sin 3 ₁ +As ₃ cos 3 ₁ ) 2 + ( R + s _min )( R + 2 D + s _min 5.

Предполагается, что центр сферической головки бедра расположен в точке O (0,0,0), а центр сферического хряща - в точке O ₁ ( x -Ae ₁, y -As ₂, z + As ₃ ) ; эксцентриситет имеет величину D (см. рис. 2).

Безразмерная функция s ₁ = s ( ф , 3 _{1 s} )/ s _Ts ( ф , 3 ₁) (где 3 _{1 s} =3 _s/ R , 3 ₁ =3/ R ) описывает изменения высоты щели при импульсивном движении, вызванном приложенной силой P . Высота щели возрастает при s ₁ >  0 и убывает при s ₁ <  0. Символ го ₀ обозначает угловую скорость в с " ¹ и описывает временные изменения возмущений при нестационарном течении синовиальной жидкости в щели сустава в радиальном направлении. Если безразмерное время 1 ₁ возрастает, то при s ₁ >  0 увеличенная высота щели уменьшается, а при s ₁ <  0 уменьшившаяся высота щели возрастает; в обоих случаях через достаточно большой промежуток времени после импульса она достигает одного и того же не зависящего от времени значения s _Ts (см. рис. 2).

Если t 1 стремится к бесконечности, т.е. N стремится к нулю, то уравнение (36) стремится к виду классического уравнения Рейнольдса в сферических координатах, но для случайных условий. После заключительных вычислений получаем уравнение:

1^ sin 31 5ф

(s T1 s + 332 s T1 s )дф

+ ^|" (sT1 s + 3°2sT1 s )|p0sin 31 d31 Lv               ' d31

= 6 ^{ds T 1 s} sin 3 ₁, (39) 5ф

где п/8 < 3 ₁ <  л/2, 0 < ф <  2 л0 ₁, 0 < 6 ₁ <  1.

Если среднеквадратическое отклонение стремится к нулю ( σ ₁ → 0 ), уравнение (39) принимает вид классического уравнения Рейнольдса для стационарного течения без случайных условий.

• 6.    Численные результаты

  Модифицированное стохастическое уравнение Рейнольдса (31), (36) определяет безразмерное давление p 10 для импульсивного движения в смазочной области Ω (0 ≤ ϕ≤ 2 πθ ₁, π/ 8 ≤ ϑ ₁ ≤ π/2) с учетом соотношений для высоты щели (37), (38). Численные расчеты проведены с помощью метода конечных разностей [14]. В расчетах принят одинаковый радиус сферической головки бедра естественного сустава и сферической головки искусственного сустава R =0,0265 м . Кроме того, для естественного и искусственного сустава мы принимаем одинаковые величины угловой скорости импульсивных возмущений вертлужной впадины ω ₀ =0,5 с^-1 и угловой скорости сферической головки бедра ω =1,5 с¹, а также одинаковое характерное размерное время t ₀ =0,000001 с. Высота щели взята в виде (37), (38), где для естественного и искусственного тазобедренного сустава мы принимаем следующие компоненты эксцентриситета головки: Δε ₁ =4,0 мкм, Δε ₂ =0,5 мкм, Δε ₃ =3 мкм. При расчетах мы взяли безразмерное среднеквадратическое отклонение σ ₁ =0,3645 для искусственного и естественного сустава.

Характерная размерная величина высоты щели равна ε ₀ =10 мкм для естественного сустава и ε ₀=3 мкм для искусственного сустава.

В естественном суставе мы принимаем динамическую вязкость синовиальной жидкости равной η ₀ =0,40 Па∙с . Кроме того, мы принимаем следующие данные: коэффициент псевдопластичности β =0,0000003 Па∙с², плотность синовиальной жидкости ρ =1010 кг/м³ . В интервале времени 0,000001 с ≤ t ≤ 100 с минимальная безразмерная величина высоты щели min( ε _{T 1 s} ) изменяется в пределах от 0,464 до 0,697 (соответствующая размерная величина изменяется от 4,6 мкм до 6,97 мкм) .

Для искусственного сустава мы предполагаем, что динамическая вязкость биологической жидкости имеет величину η ₀ =0,15 Па∙с и принимаем коэффициент псевдопластичности β =0,0000001 Па∙с² и плотность биологической жидкости ρ =1010 кг/м³. Минимальная безразмерная величина высоты щели min( ε _{T 1 s} ) изменяется в интервале времени 0,000001 с ≤ t ≤ 100 с и достигает величин от 0,933 до 1,399 (размерная высота щели изменяется от 2,798 мкм до 4,197 мкм) .

Средний относительный радиальный зазор ψ = ε₀ / R имеет величину 3,8 ⋅ 10 ^{- 4} для естественного сустава и 1,1 ⋅ 10 ^{- 4} для искусственного сустава.

Характерное размерное давление p ₀ = ωη ₀ I ψ ² достигает величины 4,2135 МПа для естественного сустава и 17,55625 МПа для искусственного сустава.

Для естественного сустава мы имеем следующие величины: число Струхала Str=666666, Re ⋅ Str=0,252, De ⋅ Str=0,7503. Для искусственного сустава имеем Str=666666, ReStr=0,061 и De ⋅ Str=0,667. В обоих случаях мы имеем 0 ≤ β/η ₀ t <  1 .

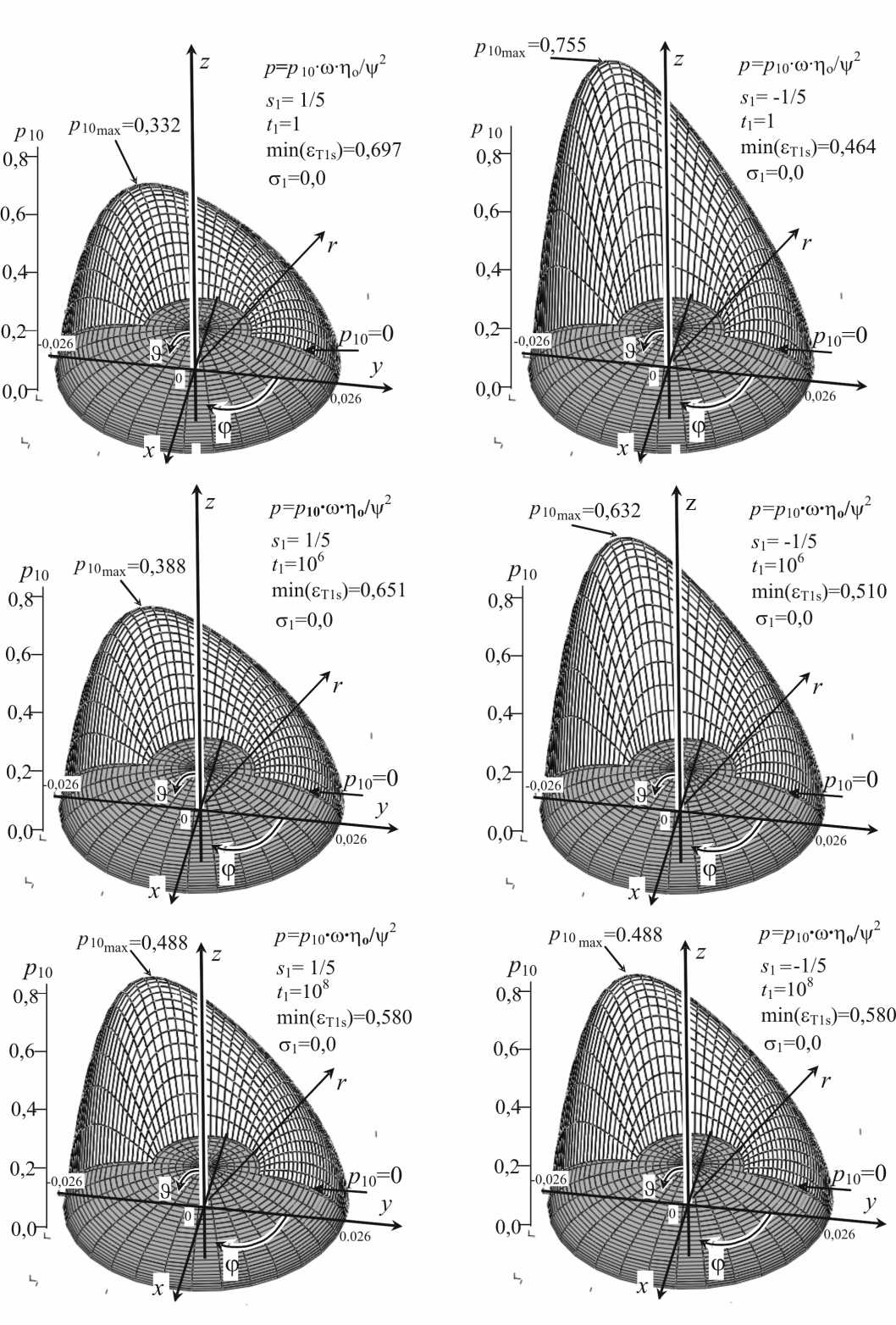
Рис. 5. Распределение размерного гидродинамического давления внутри щели естественного сферического тазобедренного сустава человека в области Ω : 0 ≤ϕ≤π , n R /8 <3<п R /2 без стохастических изменений ( о ₁=0) в моменты времени: 1 1 =1 (т.е. 1=0,000 001 с), 1 1 =1000 000 (т.е. 1 =1 с), 1 1 =100 000 000 (т.е. 1 =100 с) после приложения импульса для случаев уменьшения (слева) и увеличения (справа) высоты щели, Результаты получены для следующих исходных данных: R =0,0265 м; п 0 =0,40 Па^с; в =0,0000003 Па-с²; р =1010 кг/м³; £ _o=10 мкм , Ае ₁=4 мкм; Ае ₂=0,5 мкм; Ае ₃=3 мкм ; у=е / R ^ 3,8 - 10 ⁴; ш =1,5 с ^{- 1} ; to _o=0,5 с ^{- 1} ;

Str=666 666; Re - Str=0,252; De - Str=0,7503

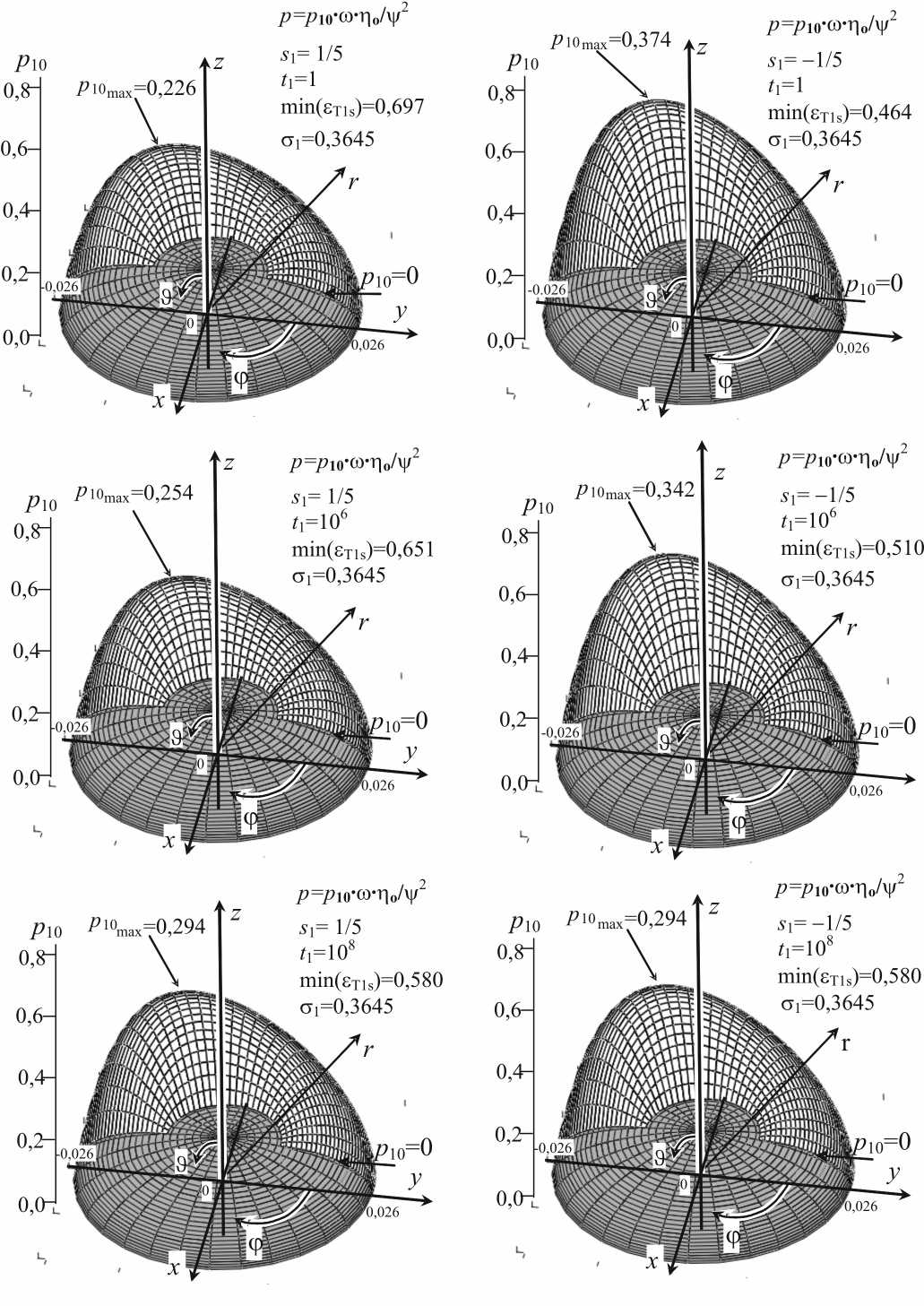
Рис. 6. Распределение размерного гидродинамического давления внутри щели естественного сферического тазобедренного сустава человека в области Ω : 0 ≤ϕ≤π , n R /8 <3<л R /2 для стохастических изменений со среднеквадратическим отклонением 0 1 =0,3645 (т.е. 3,36 мкм ) в моменты безразмерного времени: 1 1 =1 (т.е. 1 =0,000 001 с), 1 1 =1000 000 (т.е. 1=1 с), 1 1 =100 000 000 (т.е. 1 =100 с) после приложения импульса для случаев уменьшения (слева) и увеличения (справа) высоты щели, Результаты получены для следующих исходных данных: R=0,0265 м; η 0 =0,40 Па∙с; β =0,0000003 Па∙с²; ρ =1010 кг/м³; г _о=10 мкм , Ас 1 =4 мкм; Аг ₂=0,5 мкм; Аг ₃=3 мкм ; у-с R « 3,8 - 10 - 4 ; ю =1,5 с ^{- 1} ; ю _о=0,5 с ^{- 1} ;

Str=666 666; Re - Str=0,252; De - Str=0,7503

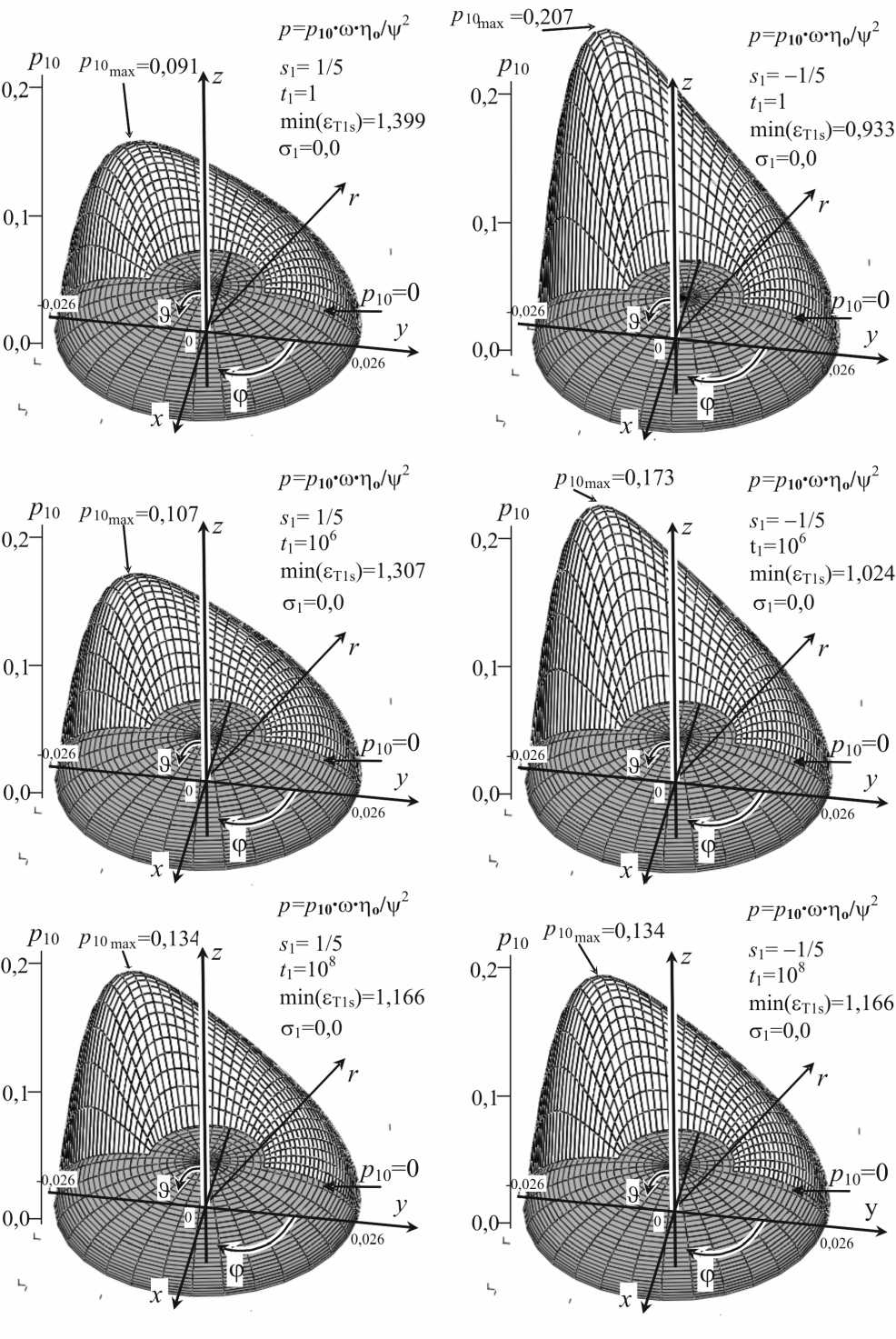
Рис. 7. Распределение размерного гидродинамического давления внутри щели искусственного сферического тазобедренного сустава человека в области Ω : 0 ≤ϕ≤π , n R /8О <п R /2 без стохастических изменений ( с 1 =0) в моменты времени: 1 1 =1 (т.е. t =0,000 001 с), 1 1 =1000 000 (т.е. t=1 с), 1 1 =100 000 000 (т.е. t =100 с) после приложения импульса для случаев уменьшения (слева) и увеличения (справа) высоты щели, Результаты получены для следующих исходных данных: R =0,0265 м; п 0 =0,15 Па^с; в =0,0000001 Па^с²; р =1010 кг/м³; s _o=3 мкм , As 1 =4 мкм; As ₂=0,5 мкм; As ₃=3 мкм ; v=s / R ~ 1,1 - 10 - 4 ; ю =1,5 с ^{- 1} ; w _o=0,5 с ^{- 1} ;

Str=666 666; Re - Str=0,061; De - Str=0,667

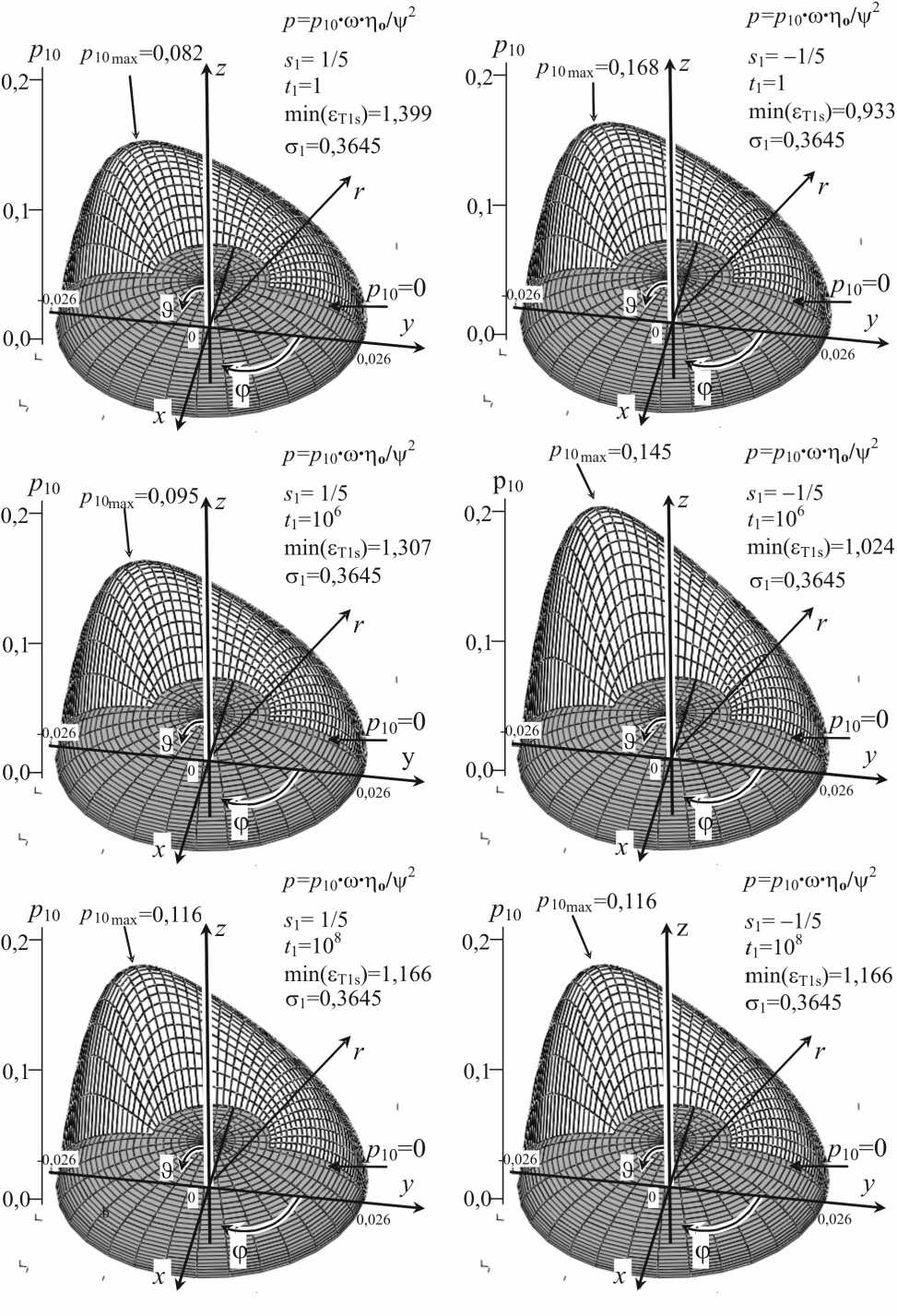
Рис. 8. Распределение размерного гидродинамического давления внутри щели искусственного сферического тазобедренного сустава человека в области Ω : 0 ≤ϕ≤π , n R /8О <п R /2 для стохастических изменений со среднеквадратическим отклонением с 1 =0,3645 (т.е. 1,08 мкм) в моменты времени: 1 1 =1 (т.е. 1=0,000 001 с), 1 1 =1000 000 (т.е. t=1 с), 1 1 =100 000 000 (т.е. 1 =100 с) после приложения импульса для случаев уменьшения (слева) и увеличения (справа) высоты щели. Результаты получены для следующих исходных данных: R =0,0265 м; п 0 =0,15 Па^с; в =0,0000001 Па^с²; р =1010 кг/м³; £ o =3 мкм , Дв 1 =4 мкм; Де ₂=0,5 мкм; Де ₃=3 мкм ; ^=е / R « 1,1 - 10 - 4 ; ® =1,5 с ^{- 1} ; ш _о=0,5 с ^{- 1} ; Str=666 666;

Re ⋅ Str=0,061; De ⋅ Str=0,667

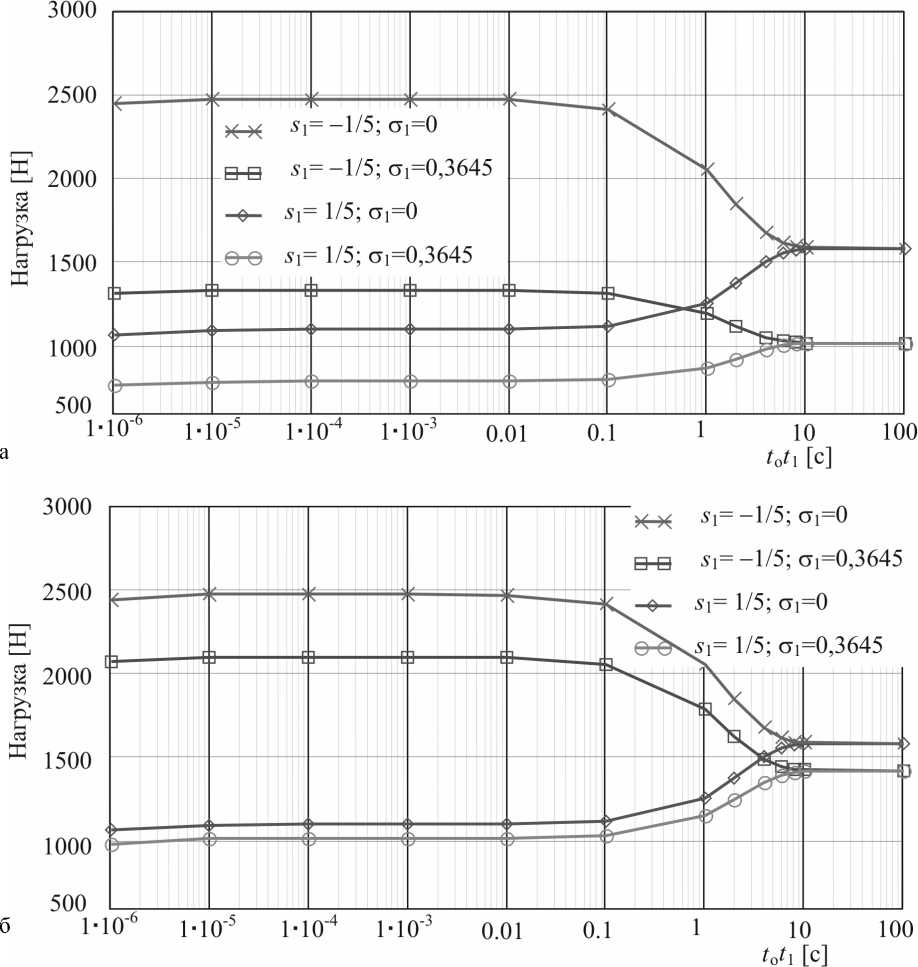
Рис. 9. Зависимость размерных величин нагрузки от размерного времени от 10^-6 секунд до 100 секунд после импульса внутри щели сферического тазобедренного сустава человека в области Ω : 0 ≤ϕ≤π , π R /8 ≤ϑ≤π R /2 для случаев: a) естественного сустава со стохастическими изменениями шероховатости поверхности хряща со среднеквадратическим отклонением σ 1 =0,3645 (т.е. 3,36 мкм) и без случайных эффектов (при σ 1 =0). Результаты получены для следующих исходных данных: R =0,0265 м; η 0 =0,40 Па∙с; β =0,0000003 Па∙с²; ρ =1010 кг/м³; ε o =10 мкм , Δε 1 =4 мкм; Δε 2 =0,5 мкм; Δε 3 =3 мкм ; ψ≡ε / R ≈ 3,8 ⋅ 10 ^{- 4}; ω =1,5 с ^{- 1} ; ω o =0,5 с ^{- 1} ; Str=666 666; Re ⋅ Str=0,252; De ⋅ Str=0,7503; б) искусственного сустава со стохастическими изменениями шероховатости поверхности хряща со среднеквадратическим отклонением σ 1 =0,3645 (т.е. 1,08 мкм) и без случайных эффектов (при σ 1 =0). Результаты получены для следующих исходных данных: R =0,0265 м; η 0 =0,15 Па∙с; β =0,0000001 Па∙с²; ρ =1010 кг/м³; ε o =3 мкм , Δε 1 =4 мкм; Δε 2 =0,5 мкм; Δε 3 =3 мкм ; ψ≡ε /R ≈ 1,1 ⋅ 10 ^{- 4}; ω =1,5 с ^{- 1} ; ω o =0,5 с ^{- 1} ;

Str=666 666; Re ⋅ Str=0,061; De ⋅ Str=0,667

Для значений безразмерного времени t 1 =1, 1000000 и 100000000, что соответствует значениям размерного времени t =0,000001 с, 1,0 с и 100,0 с, и для s 1 = ± 0,20 мы получаем распределения безразмерного давления для естественного сустава (рис. 5 и 6) и для искусственного сустава (рис. 7 и 8).

Чтобы получить реальные значения времени, нужно умножить безразмерные величины t1 на характерное время t0=0,000001 с. Например, t1=1000 000 означает 1 с после импульса. Чтобы получить размерную величину давления, нужно умножить безразмерное давление (см. рис. 5, 6, 7, 8) на величину характерного давления p0 .

На рис. 5 и 7 представлены величины безразмерного давления без случайных эффектов (при с 1 =0). Безразмерные величины давления, приведенные на рис. 6 и 8, получены для стохастических изменений высоты щели при безразмерном среднеквадратическом отклонении с 1 =0,3645. Распределения безразмерного давления, вычисленные при 5 1 >  0, представлены в правом столбце чисел на рис. 5, 6, 7 и 8. Эти величины давления получены для эффекта увеличения высоты щели, вызванного импульсивным движением. В этом случае с ростом времени после импульса высота щели уменьшается, а давление возрастает, и при достаточно большом времени после импульса стремится к стационарному давлению.

Распределения безразмерного давления для 5 1 <  0 представлены в левом столбце чисел на рис. 5-8 и получены для эффекта уменьшения высоты щели, вызванного импульсивным движением. В этом случае время после импульса растет, щель увеличивается, а давление падает, и при достаточно большом времени после импульса стремится к стационарному давлению.

На рис. 9 представлены зависимости безразмерной величины нагрузки от безразмерного времени для естественного и искусственного сустава в интервале времени от момента импульса до 100 секунд после импульса.

• 7.    Заключение

  • •    Если травма увеличивает высоту щели ( 5 1 >  0) для нормального сустава, то с течением времени после импульса высота щели уменьшается и давление растет. Если, наоборот, травма уменьшает высоту щели ( 5 1 <  0), то с течением времени после импульса высота щели возрастает и давление падает. В обоих случаях при достаточно большом времени после импульса высота щели и давление достигают стационарных значений.

  • •    Если время после импулься достаточно велико, т.е. при t 1 ^ да , и если мы берем оптимальные среднеквадратические отклонения высоты щели, то распределения давления для эффектов увеличения ( 5 ₁ >  0 ) или уменьшения ( 5 ₁ <  0 ) высоты щели из-за импульса стремятся к идентичным распределениям давления. Это граничное распределение давления можно получить также из классического уравнения Рейнольдса (39) при с 1 =0.

  • •    В результате численных расчетов мы отмечаем, что оптимальное среднеквадратическое отклонение с 1 =0,3645, определенное путем измерений поверхностей нормального хряща тазобедренного сустава человека, понижает давление и нагрузку примерно на 30% по сравнению с давлением и нагрузкой, полученных для гладкой поверхности хряща без неровностей и случайных эффектов.

  • •    Численные расчеты показывают, что наибольшие изменения нагрузки и распределения давления в человеческом суставе возникают в интервале времени от 0,1 до 10 секунд после импульса.

  • •    Из анализа численных результатов, представленных на рис. 9, легко видеть, что различия между величинами давления, полученными с учетом случайных эффектов

и без их учета, при ушибе естественного сустава значительно больше тех же различий для искусственного сустава. Этот феномен мы можем объяснить тем фактом, что поверхность головки искусственного тазобедренного сустава имеет намного меньшие неровности, чем поверхность головки бедра естественного сустава. Отсюда среднеквадратическое отклонение случайных неровностей поверхности для головки искусственного сустава намного меньше, чем для естественной головки бедра.

Благодарности

Эта статья финансировалась из фонда KBN в 2003-2006 г. как Научный Проект KBN 411E-030-25. Настоящее исследование финансово поддержано Проектом TOK– FP6-517226.