Стоячие конвективные волны в слабопроводящей жидкости

Объектом изучения электрогидродинамики являются так называемые слабопроводящие жидкости, обладающие малой электропроводностью ( σ ≤ 10 ^{- 7} - 10 ^{- 12} Ом^–1см^–1) [1]. Таковыми можно считать широкий класс жидких материалов, активно используемых в промышленности и технике: топлива, углеродные масла и жидкие диэлектрики. Малая проводимость позволяет рассматривать в них лишь электростатические взаимодействия и пренебрегать магнитными эффектами [2].

Механизм возникновения течений в подобных жидкостях под влиянием электрического поля напрямую связан со способом генерации в жидкости свободных или поляризованных зарядов [2–9]. Если генерация вызывается инжекцией, то свободный заряд появляется на границе жидкость–электрод вследствие окислительно-восстановительных электрохимических реакций [5, 10]: в приграничных зонах образуется скопление зарядов со знаком, совпадающим со знаком электродов. Вследствие одинаковости знаков заряды начинают отталкиваться от электрода, то есть в жидкости наводятся силы, влияющие на ее элементарные объемы и способные привести их в движение, возбудить течение жидкости в электрическом поле [10–12]. Этот эффект в последнее время c успехом используется в микрофлюидике [13–15].

В данной статье рассматривается униполярная инжекция с катода. В этом случае находящаяся у электрода нейтральная примесь захватывает электроны и превращается в смесь отрицательных ионов [10]:

M + (X+Y")^M(e) + (XY_)^ Yfee,

где M — металлический электрод, отдающий ионной паре ( X ⁺ Y ) электрон e , Y f _ree — инжектируемый ион. Схема (1) представляет классический пример униполярной инжекции с катода.

Отрицательный заряд, инжектируемый в жидкость вблизи катода, начинает распространяться вглубь сплошной среды. Сила Кулона, действующая на заряд в жидкости, выступает в роли возбудителя массопереноса.

В изотермической жидкости присутствие постоянного электрического поля может привести к возникновению стационарной конвекции путем обратной бифуркации [11, 12]. В зависимости от напряжения на электродах жидкость находится либо в состоянии ионной проводимости и отсутствия движения сплошной среды, либо в режиме конвективного течения под действием силы Кулона с наличием гистерезисного перехода между этими двумя состояниями. В неизотермическом же случае, кроме этих состояний, существуют надкритические нелинейные волновые структуры, разнообразие которых представляет интерес и с теоретической, и с практической точек зрения. Важным для приложений результатом подобных исследований является возможность управления теплопереносом в жидкости как в сторону его усиления [16, 17], так и ослабления [18]. С позиции теории имеют интерес, например, наблюдения хаотических колебательных течений при нагреве замкнутой полости сбоку [19].

Результаты анализа надкритических режимов конвекции в электрическом поле при нагреве сверху, проведенного в безындукционном приближении для заряда на катоде, пропорционального приложенному полю [10, 20, 21], демонстрируют возникновение в жидкости колебательной неустойчивости и повышение порога при переходе к стационарным режимам. В результате прямой бифуркации Хопфа рождаются волновые конвективные течения: стоячая волна (SW), бегущая волна (TW), модулированная бегущая волна (MTW), модулированная стоячая волна (MSW), которые могут реализоваться в горизонтальном слое или кольцевом канале. Такое поведение слабопроводящей жидкости связано с перераспределением заряженной примеси в объеме и в некотором смысле представляется аналогом конвекции бинарных смесей [22], в которых при эволюции колебательных возмущений могут образовываться стационарные и волновые структуры, в том числе стоячие и бегущие волны, активно изучаемые путем численного моделирования [23, 24].

Текущее исследование является продолжением работы [25], в которой изучаются нелинейные устойчивые режимы конвекции в постоянном электрическом поле при униполярной автономной инжекции заряда и нагреве сверху в полной электрической постановке. В данной работе найдены и проанализированы режимы неустойчивых стоячих волн, а также построена полная бифуркационная диаграмма волновых конвективных решений.

2.    Постановка задачи

Вязкая несжимаемая слабопроводящая жидкость с динамической вязкостью п , температуропроводностью % , подвижностью зарядов K и диэлектрической проницаемостью б помещена в плоский бесконечный конденсатор толщиной d . На обкладках конденсатора поддерживается постоянная разность температур 0 и постоянная разность потенциалов V 0 таким образом, что жидкость нагревается сверху, и на верхней же обкладке конденсатора производится автономная униполярная инжекция отрицательных зарядов с плотностью q ₀ (верхняя обкладка является катодом). Помимо прочего, на жидкость действует сила тяжести g .

Рассмотрим вертикальный разрез конденсатора. Проведем ось x вдоль верхней обкладки конденсатора, а ось z внутрь слоя жидкости. Тогда получим геометрию задачи (Рис. 1). Положим линейной зависимость

0(0)=6, Ф(0)=0

л © © © © © © © © © © ^

между плотностью жидкости ρ и отклонением температуры от средних значений 9 : р = р₀ ( 1 - в9 ) ,

v

ею=о, Ф(бО=г0

Рис. 1. Геометрия задачи и граничные условия

где ρ0 — плотность жидкости при средней температуре, а β — коэффициент объемного расширения жидкости. Жидкость считаем несжимаемой, так что зависимость плотности жидкости от давления во внимание не принимаем.

В силу малости в уравнении динамики жидкости как коэффициента объемного расширения жидкости, так и

конвективных слагаемых по сравнению с массовыми силами, неоднородность плотности можно учесть лишь в слагаемых, связанных с этими силами (то есть следует воспользоваться приближением Буссинеска [26]). Другим важным приближением является так называемое ЭГД-приближение, согласно которому, ввиду малой электропроводности жидкости и токов зарядов в ней, игнорируются магнитные эффекты [1]. Кроме того, при электропроводности жидкости в пределах 10-9 -10-11 Ом-1м-1 и напряженности электрического поля E|2 < 105 В/м в уравнении теплопроводности можно пренебречь слагаемым, связанным с джоулевым нагревом [2].

Для записи основных уравнений системы в безразмерной форме применим при обезразмеривании параметров следующие масштабы: для длины — d ; времени — d ²р ₀ /р ; скорости — п/ ( р ₀ d ) ;

температуры — 0 ; давления — п 2 Др₀ d ² ) ; электрического потенциала Ф — V ₀; плотности заряда q —

£ ₀ £ V 0 [d ², где £ 0 — диэлектрическая постоянная.

Система физических уравнений, решением которой являются стоячие конвективные волны в слабопроводящей жидкости, включает уравнение Навье–Стокса, закон сохранения заряда, уравнение теплопроводности, условие несжимаемости жидкости и дифференциальный закон Гаусса в терминах потенциала и объемной плотности заряда (уравнение Пуассона) [11, 16, 26]. С учетом принятых приближений они выглядят так:

• — + (vV) v = -Vp + Av - T— qVO - Ra 0e, dt V ’               M2 Pr

  <

  
  

⁺⁽v^V ) q = M ( q ² -^{V Ф} '^V q ) •

—+ (vV)0 = — A0, dt V ’ Pr div v = 0,

АФ = - q,

где t — время, v — скорость, p — давление, q — плотность заряда, Ф — электрический потенциал, e — единичный вектор, сонаправленный с осью z , V и А — стандартные дифференциальные операторы. Наличие уравнения Пуассона в системе (2) свидетельствует о том, что во внимание берется изменение электрического поля внутри конденсатора, обусловленное перераспределением заряда, то есть задача рассматривается в полной электрической постановке.

Запишем граничные условия. Считаем обкладки конденсора идеально проводящими с условием прилипания жидкости, тогда на горизонтальных границах имеем:

z = 0 : v = 0, 0 = 1, Ф = 0, q = С , z = 1: v = 0,   0 = 0, Ф = 1.

Система уравнений (2) и условия (3) содержат ряд безразмерных комплексов, имеющих следующий

,, D   ро gРd 30      _                      , £ £ V Ро /_ смысл: число Релея Ra = —0-----; электрическое число Релея T = ———- (параметр, характеризующий

ПХ конвекцию в электрическом поле и пропорциональный напряжению на обкладках); число Прандтля п                                                 / £0£    „ _       - „      _

Pr =--- ; параметр подвижности ионов M = —0—; постоянный параметр инжекции С = —⁰— ,

Р0Х                                                K Р0

где q ₀ — плотность заряда, инжектируемого на катоде.

Необходимо отметить, что течения заряженных сред часто представляются другой моделью — моделью Нернста–Планка [27], где физические носители заряда (анионы и катионы) имеют разные знаки. Для униполярной инжекции (1) характерен только один тип носителей — отрицательный заряд, который создается на катоде за счет окислительно-восстановительных электрохимических реакций. Диэлектрическая жидкость не обладает остаточной проводимостью и, следовательно, не имеет положительных носителей.

Проанализируем систему (2) совместно с граничными условиями (3). В уравнении Навье–Стокса, описывающем динамику сплошной среды, присутствуют слагаемые, отвечающие за внешние силы, действующие на элементарный объем жидкости, то есть за силу Кулона и за силу плавучести (силу Архимеда).

Сила Кулона совпадает по направлению с силой тяжести, и растворенный в жидкости отрицательный заряд от верхней обкладки конденсатора (катода) перемещается вниз. Если бы жидкость была изотермической, то при превышении напряжением на обкладках конденсатора некоторых критических значений произошло бы жесткое возбуждение конвективного движения [11, 12]. Однако в рассматриваемой задаче жидкость находится под постоянным нагревом сверху, силы плавучести возвращают ее обратно к катоду, что приводит к существованию области надкритических волновых режимов. Вместе с тем, если бы силы Кулона отсутствовали или были незначительными по сравнению с силами плавучести, то при умеренном нагреве сверху жидкость оставалась бы устойчивой и движение бы в ней не возникало.

Таким образом, в данной постановке ответственным за конвекцию в жидкости можно считать инжекционный механизм, а термогравитационный механизм неустойчивости (при нагреве сверху) сам по себе конвекцию не вызывает, но порождает колебательные режимы течения.

3.    Метод решения задачи

Сформулированная постановка задачи подразумевает ряд упрощений, которыми необходимо воспользоваться для подготовки к численному решению.

Во-первых, имеет смысл рассмотреть лишь двумерные возмущения: v = ( v x ,0, v z ) . С одной стороны, это корректно по причине отсутствия в системе (2) слагаемых, содержащих силы, направленные перпендикулярно вертикальной плоскости задачи, а значит уравнения инвариантны относительно выбора направления оси x . С другой стороны, в реальных задачах определенной геометрии (например, в кольцевых зазорах большого радиуса) возникают именно квазидвумерные волновые режимы [21, 25]. Двумерность задачи позволяет прибегать к классическому двухполевому методу, исключающему из уравнений Навье–Стокса давление.

Согласно двухполевому методу, введем две функции, связанные со скоростью жидкости:

Ш       ОШ

к =--, v, = —, го = ( rot v) = -Аш,

x дz          дx        V ’ y где ш(x,z , t) называется функцией тока, а го(x,z, t) — вихрем скорости. Тогда условия на горизонтальных границах примут вид:

z = 0: _v = 0, ^Ги 0, 0 = 1, ф = 0, q = C д z

z = 1: _v = 0, ^Ги 0, 0 = 0, ф = 1. д z

Второе допущение, принятое в постановке, — бесконечность слоя вдоль горизонтального направления, требует введения определенных граничных условий, которые будут представлены в следующем разделе.

Систему дифференциальных уравнений с граничными условиями, записанную для функций ш , ^ю , q , 0 и Ф , проинтегрируем численно, при помощи методов конечных разностей [12, 31].

В [28] показано, что явная схема с центральными разностями, применяемая к конвективным и вязким слагаемым в уравнении Навье–Стокса, будет зависимой от локального критерия устойчивости, в качестве которого здесь выступает сеточное число Рейнольдса. При превышении этим числом некоторого критического значения для сохранения устойчивости решения необходимо переключаться на схему с разностями против потока, которая имеет меньший порядок аппроксимации, чем центрально-разностная, но устойчива при достаточно малых шагах по времени. Гладкий переход между двумя явными схемами реализует специальная процедура.

Уравнения теплопроводности и закон сохранения заряда аппроксимируем явными схемами против потока. Оба уравнения Пуассона (для электрического потенциала и для функции тока) разрешим методом последовательной верхней релаксации на каждом временном шаге. На горизонтальных границах для вихря скорости го применим условия Тома [12, 28].

Для дискретизации расчетной области используем сетку с 21×41 узлами и шагом по пространству h = 0,05, шаг по времени выберем в соответствии с критериями устойчивости конечноразностных схем в зависимости от скорости движения жидкости. Измельчение выбранной сетки не приводит к качественным изменениям в результатах [25].

Для анализа решения задачи рассмотрим как локальные, так и интегральные характеристики системы. Основной исследуемой функцией является функция тока ш , поэтому возьмем ее максимальное значение внутри ячейки в каждый момент времени: ш _тах ( t ) = max [v i j ( t k ) ] ■ Координаты максимального значения функции внутри ячейки отвечают положению центра одного из конвективных валов. Помимо этого, построим распределения основных функций системы внутри ячейки.

Пространственно-временное распределение полей функции тока в ряды Фурье по гармоникам F n ( t ) (например, в горизонтальном направлении в сечении, соответствующем середине высоты слоя z = 1/2 ):

F lx, z = -, t| = f° (t )+£fn (t)    ,                                    (6)

V ² 7              n = 1

позволяет охарактеризовать особенности различных течений жидкости. Для описания возникающих в жидкости структур в анализируемом случае достаточно информации о первой — у ₁ ( t ) , и второй — ф ₂ ( t ) , модах разложения функции тока; вклад третьей гармоники \j/ 3 ( t ) в общее решение мал (не превышает 1%).

4.    Результаты исследования

Для численного моделирования системы использовались те же значения безразмерных параметров, что и в [25]: число Релея Ra = - 2500 ; число Прандтля Pr = 10. Параметр подвижности ионов M , способный принимать широкий набор значений 4 <  M <  120, в рассматриваемой задаче принимался равным 14,14 (это наиболее часто применяемое значение [8, 10, 15]). Параметр C = - 0,224 соответствовал умеренной униполярной инжекции (0,2 <  C <  5) [11]. В качестве жидкости с подобными параметрами может выступать этиловый спирт с ионами хлора, в размерных величинах значения параметров системы отвечали толщине зазора d ~1,5 мм и напряжению на обкладках конденсатора V ₀ ~ 4,2 кВ.

• 4.1.    Покоящаяся жидкость

В случае, когда управляющий параметр системы (электрическое число Релея) мал, жидкость покоится (конвективный массоперенос не возникает). Кроме того, в данной задаче в слое жидкости отсутствует горизонтальная анизотропия, и все функции зависят лишь от вертикальной координаты. Таким образом, задача поддается аналитическому решению. При этом уравнение теплопроводности сводится к тривиальному дифференциальному уравнению с решением для отклонения температуры от средних значений в равновесном состоянии в виде линейной зависимости:

• ^О ° = ¹ - z ,

а уравнение сохранения заряда — к одномерному нелинейному дифференциальному уравнению, которое имеет псевдоаналитическое решение для равновесного распределения заряда q ₀ и потенциала Φ₀ :

3 C ² ( 2 Cz + 1 )^{- 1/}2               1 - ( 2 Cz + 1 ) 32

1 - ( 2 C + 1 ) 32 ,         °    1 - ( 2 C + 1 ) 32

3 C ²

где С =----₌---== . Видно, что получить обратную аналитическую зависимость C = f ( C ) нельзя, однако

1 - ( 2 C + 1 ) 32

можно для каждого рассматриваемого значения C численно определять величину C . Например, принятому в данной работе значению С = - 0,224 соответствует значение C = 0,25 . Стоит отметить, что найденные для q ₀ и Φ₀ решения качественно и количественно совпадают с таковыми в том случае, когда инжектируемый заряд зависит от напряженности электрического поля [10]. Они позволяют анализировать поведение параметров системы с точки зрения отклонений от равновесных значений.

• 4.2.    Периодические граничные условия по горизонтали

В работе [25] изучались бегущие волны в задаче аналогичной геометрии (см. Рис. 1) при периодических граничных условиях по горизонтали с периодом l = 2 (такому периоду отвечает волновое число к = 2л/ 1 = п — критическое значение возникновения термогравитационной конвекции). При этом жидкость нагревалась снизу в отсутствие электрических взаимодействий:

F ( x , z , t ) = F ( x + 1 , z , t ) ,

где F — любая из функций системы (2)–(4). Кратко напомним результаты, важные для дальнейшего изложения. Далее используются обозначения, принятые в работе [25].

При последовательном увеличении управляющего параметра T в равновесной жидкости образуется конвекция путем прямой бифуркации Хопфа в виде смешанного режима (M) при значении T _c 1 = 6805. С увеличением значения электрического числа Релея жидкость переходит к режиму бегущих волн (TW), характеризующемуся смещением конвективной структуры (смещением полей функции тока, температуры, электрических заряда и потенциала) вдоль горизонтального направления с постоянной фазовой скоростью. Режим бегущих волн является основным режимом конвекции в надкритической области и существует при T е [ T _c 2 = 6818,7037 ] . Перед тем, как перейти к высокоинтенсивному режиму стационарной конвекции

(SOC) при T > T _c 4 = 7061, в системе непродолжительное время наблюдается режим модулированных бегущих волн (MTW) при T е [ T _c 3 = 703 8,7060 ] . Остановимся на смешанном режиме (M) более подробно.

Смешанный режим M во многом похож на стоячие волны (Рис. 2). В течение большей части периода в ячейке наблюдаются два конвективных вала, закрученных в противоположные стороны. Интенсивность конвекции в них периодически то уменьшается, то увеличивается, а при достижении интенсивностью конвекции минимальных значений конвективные валы меняются местами. Отличие от «чистых» стоячих волн обнаруживается как раз в те моменты времени, когда интенсивность конвекции в валах мала и конвективная структура смещается вдоль горизонтального направления скачком, что и приводит к перестановке валов. Скорее всего такой режим возникает из-за того, что две волновые компоненты функции тока, двигающиеся во встречных направлениях и образующие итоговое распределение, не идентичны друг другу и в них проявляются высшие гармоники.

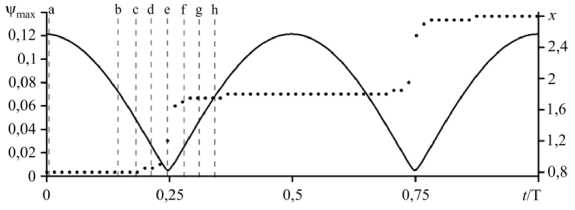
Рис. 2. Зависимость от времени максимального значения функции тока в ячейке (сплошная линия и левая вертикальная ось) и x -координаты максимума функции тока в ячейке (пунктирная линия и правая вертикальная ось) в смешанном режиме M; T = 6815; буквами a, b, …, h обозначены характерные моменты времени

Смешанный режим показывает, что в системе есть потенциал для существования чисто стоячих волн (SW), как в задачах конвекции в постоянном [8, 16] или переменном поле [23, 24]. Но при использовании полностью периодических условий в данной постановке, и даже при модуляции потенциала на обкладках со временем [31], стоячие волны являются неустойчивыми. Поэтому, для их отыскания требуется задание специальных граничных условий на вертикальных границах, исключающих существование бегущих волн.

• 4.3.    Граничные условия для моделирования стоячих волн

Для температуры, потенциала и заряда, как и ранее, запишем периодические граничные условия, а для функции тока будем иметь:

V ( nl , z , t ) = 0, n е N .

Такие граничные условия из всего набора периодических по горизонтали решений выделяют решение с узлами функции тока на вертикальных границах, что соответствует стоячей волне. Можно представить, что внутрь конденсатора на расстоянии l друг от друга помещаются вертикальные мембраны, которые

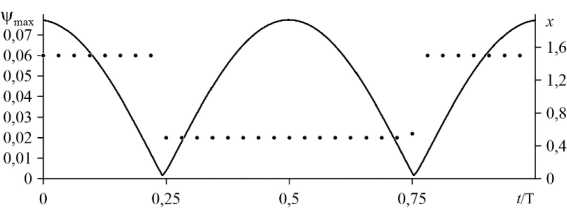
Рис. 3. Зависимость от времени максимального значения функции тока в ячейке (сплошная линия и левая вертикальная ось) и x -координаты максимума функции тока в ячейке (пунктирная линия и правая вертикальная ось) в режиме стоячих волн SW; T = 6810

идеально тепло- и электропроводны, но не пропускают через себя жидкость. С таким ограничением конвекция в жидкости появляется при том же критическом значении электрического числа Релея — T _c 1 = 6805 , путем прямой бифуркации колебательным образом, но теперь в виде чисто стоячих волн SW (Рис. 3).

Сравним поведение системы в режиме стоячих волн (SW) и смешанном режиме (M) (Рис. 3 и 2). Как можно заметить, на графиках обнаруживается два существенных различия. Во-первых, в режиме стоячих волн при смене положения конвективных валов интенсивность конвекции в них действительно стремится к нулю, а не к какому-то малому значению, как в смешанном режиме. Во-вторых, положение максимумов функции тока (центров конвективных валов) меняется скачкообразно, а не плавно в режиме смешанных волн.

На рисунке 4 изображено пространственное распределение некоторых характеристик системы вблизи максимума интенсивности конвекции в режиме стоячих волн SW. Качественно они не отличаются от аналогичных распределений в смешанном режиме M [20].

Рис. 4. Распределения в ячейке отклонений от равновесных значений: отклонения температуры (а), плотности заряда (б), электрического потенциала (в) в режиме стоячих волн SW, T = 6810 ; на каждом из распределений показаны изолинии функции тока (сплошная линия – положительные значения, штриховая – отрицательные)

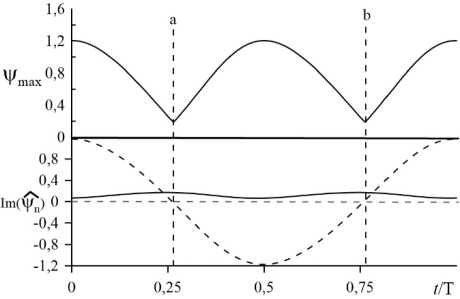
Рис. 5. Зависимость от времени максимального значения функции тока в ячейке (верхний график) и коэффициентов при мнимых гармониках разложения в ряд Фурье функции тока (нижний график, штриховая линия – первая гармоника, сплошная линия – вторая гармоника) в режиме модулированных стоячих волн MSW, T = 6910

Режим стоячих волн существует при T е [ Т _с 1 = 6805,6864 ] . При T g [ T ' 2 = 6865,6018 ] в системе реализуется режим модулированных стоячих волн (MSW). Символом со штрихом обозначены критические числа T, соответствующие переходам между различными неустойчивыми решениями. Режим MSW отличается от режима стоячих волн тем, что при уменьшении интенсивности конвекции в ячейке перестановка конвективных валов выглядит как появление в системе второй пространственной гармоники. Видно, что в те моменты времени, когда интенсивность конвекции в ячейке достигает минимальных (но ненулевых) значений (см. моменты a и b, Рис. 5), мода первой пространственной гармоники становится равной нулю, но при этом мода второй пространственной гармоники (7)

положительна и максимальна. Ввиду этого в ячейке наблюдаются две пары закрученных в противоположные стороны конвективных валов (Рис. 6).

Рис. 6. Распределения в ячейке отклонений от равновесных значений: отклонения температуры ( а ), плотности заряда ( б ), электрического потенциала ( в ) в режиме модулированных стоячих волн MSW; T = 6910 ; распределения соответствуют разрезу a рисунка 5, на каждом из них показаны изолинии функции тока (сплошная линия – положительные значения, штриховая – отрицательные)

При значениях T >  Т' _с 3 = 6019 система переходит к высокоинтенсивному режиму стационарной конвекции SOC. Обобщить данное исследование можно добавлением обнаруженного неустойчивого режима стоячих волн (Рис. 7) к бифуркационной диаграмме устойчивых надкритических режимов конвекции, описанных выше в разделе 4.2 и в статье [20].

Здесь имеет смысл обратить внимание на два наблюдения: во-первых, в случае как устойчивых, так и неустойчивых режимов конвекция возникает одинаково, при одном и том же критическом значении управляющего параметра путем прямой бифуркации колебательным образом; во-вторых, переход к высокоинтенсивному режиму движения жидкости происходит в тот момент, когда максимальное значение функции тока в ячейке достигает одинакового критического значения у max = 1,31.

Ранее конвекция в слабопроводящей жидкости рассматривалась для случая нагрева сверху и униполярной инжекции в зависимости от напряженности электрического поля: q ( z = 0 ) = - A • Ez [10, 20]. Однако, в дополнение к бегущим и модулированным бегущим волнам, карта бифуркаций содержит решения в виде устойчивых стоячих волн, которые при автономной инжекции отсутствуют. Следует отметить, что в обеих задачах (с постоянной инжекцией и с зависящей от напряженности электрического поля) на картах бифуркаций имеются общие черты: волновые режимы конвекции возникают в результате прямой бифуркации; при достаточно больших значениях электрического числа Релея волновые решения становятся неустойчивыми и происходит интенсивная стационарная конвекция.

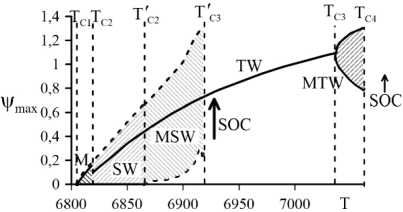
Рис. 7. Бифуркационная диаграмма режимов конвекции в виде зависимости максимального значения функции тока от электрического числа Релея; сплошные линии соответствуют устойчивым режимам конвекции, штриховые – неустойчивым; заштрихованные области подразумевают, что в них максимальное значение функции тока с течением времени меняется в некоторых пределах

5.    Заключение

Обнаружены и изучены режимы стоячих и модулированных стоячих волн в заполняющей плоский горизонтальный конденсатор слабопроводящей вязкой несжимаемой жидкости при наличии автономной униполярной инжекции заряда с катода и нагреве жидкости сверху. Анализ пространственных распределений и гармоник функции тока показал, что в режиме модулированных стоячих волн в ячейке периодически появляется структура, содержащая две пары закрученных в противоположные стороны конвективных валов (четыре конвективных вала).

Построена полная бифуркационная диаграмма волновых режимов течения жидкости при нагреве снизу/сверху и при воздействии/в отсутствие электрического поля. Показано, что условия возникновения и исчезновения (разрушения) надкритических режимов одинаковы для устойчивых и неустойчивых решений.