Стратегическая рефлексия в матричных играх
Автор: Воробьев Альберт Анатольевич, Данеев Алексей Васильевич
Журнал: Известия Самарского научного центра Российской академии наук @izvestiya-ssc
Рубрика: Информатика, вычислительная техника и управление
Статья в выпуске: 6-1 т.19, 2017 года.
Бесплатный доступ
Практическое применение матричных игр исторически существенно ограничивается принципиальной невозможностью в большинстве случаев реализации несовместных смешанных стратегий. С целью расширения области применения результатов решения матричных игр в статье разработана новая классификация игр двух лиц с нулевой суммой и конечным числом стратегий. Показаны практические трудности реализации решений теоретико-игровых моделей конфликтных ситуаций типа «оборона-нападение» в смешанных стратегиях. Для матричных игр этого класса на основе проведенных экспериментальных исследований сформулированы правила целенаправленного улучшения решений на основе применения стратегической рефлексии. Для итеративного метода Брауна-Робинсон решения матричных игр исследовано применение показателя оценивания точности результата непосредственно в ходе итеративного процесса.
Итеративный метод, конфликтная ситуация, матричные игры, статистические игры, улучшение стратегий
Короткий адрес: https://sciup.org/148205381
IDR: 148205381 | УДК: 519.83
Текст научной статьи Стратегическая рефлексия в матричных играх
Существующая три четверти столетия теория игр в XXI веке переживает свой ренессанс. Стремительно развиваются принципиально новые направления теории, такие как эволюционные, алгоритмические, экспериментальные, рефлексивные, сетевые и другие игры. Возникновение новых теоретических направлений обусловлено, прежде всего, практическими потребностями исследования современных явлений, процессов, систем, имеющих нередко междисциплинарную природу и объединяющих в себе организационные, социальные и технические (экономические) аспекты человеческой деятельности. Наряду с этим, развитие теории игр стимулировали традиционные проблемы, ограничивающие ее практическое применение. Общими проблемами являются сложности формализации самой теоретико-игровой ситуации (построение адекватной модели и обеспечение достоверности исходных данных выходит за рамки теории игр), а также практической реализации решений в смешанных стратегиях. Для некооперативных (некоалиционных) игр критичными стали «классические» ограничения на информированность сторон (игроков, агентов), а также существование множества равновесных ситуаций и трудности их нахождения.
Основные признаки различных игровых постановок с развитием теории также существенно трансформировались. Новые классы игр стали различаться не только по структуре математических моделей, но и по характеру исследуемого объекта и/или по степени информированности сторон (как о состоянии моделируемых процессов, так и о взаимных возможностях). Отличиями неоклассических теоретико-игровых постановок, по сравнению с традиционными классическими, явились, в частности, возможности исследования:
-
- существенно новых объектов - например, сетевые игры для исследования различных процессов в социальных сетях [1-3];
-
- поведения больших однородных групп агентов в типичных повторяющихся конфликтных ситуациях, при достаточно слабых предположениях относительно их информированности – эволюционные игры , как раздел теории коллективного поведения [4-7];
-
- процессов взаимодействия принимающих решения субъектов, обладающих различными (в том числе - иерархическими) уровнями информированности о параметрах моделируемой ситуации, или о принципах принятия решений оппонентами – рефлексивные игры [8, 9];
-
- равновесных ситуаций в бескоалиционных играх, в том числе в условиях отсутствия априорной информации о динамически развивающейся моделируемой ситуации, а также робастных алгоритмов поиска решений – алгоритмические игры [10-12];
-
- процессов из области так называемой экспериментальной экономики, или из иных новых областей, например, связанных с выявлением
эффективного поведения игрока или команды в спортивных соревнованиях самого различного вида - экспериментальные игры [13-16].
Наряду с этими, активно формируется целый ряд ещё более новых направлений в теории игр. Большинство из таких направлений указаны в обзоре [17], затрагивают процессы междисциплинарной природы и не имеют пока устоявшейся терминологии.
Характерное для неоклассических игровых постановок существенное усложнение моделей привело к появлению алгоритмических проблем нахождения решений, в силу высокой сложности самих моделируемых процессов. В подобных случаях единственным способом нахождения решения может являться декомпозиция конечных игр на совокупность взаимосвязанных матричных (биматричных) [18, 19]. Следует, однако, отметить, что и сами матричные (биматричные) игры бурно развиваются и также приобретают новые черты, характерные для неоклассических постановок. Наиболее известными примерами новых постановок матричных (биматричных) игр сегодня являются:
- динамические матричные (биматричные) игры, представляющие собой совокупность взаимосвязанных матричных (биматричных) игр, распределенных на временной оси [20, 21];
- матричные (антагонистические) игры с неполной информацией, в которых известны вероятности (частоты) применения стратегий игроками, но не определены некоторые элементы платежной матрицы [22];
- различные расширения постановок задач типа «игры полковника Блотто» – при дополнительных условиях о несимметричности ресурсов, стратегической (степень знания принципов принятия решений оппонентом) или информационной (степень знания параметров моделируемой ситуации и информированности об этом оппонента) рефлексии [23].
2. КЛАССИФИКАЦИЯ И ПРАКТИЧЕСКОЕ ПРИМЕНЕНИЕ МАТРИЧНЫХ ИГР
Естественно полагать, что сложившаяся практика применения неоклассических игровых постановок позволяет расширить возможности применения и ряда классических игровых моделей. В статье исследован простейший класс теории игр – классические матричные игры (они же – игры двух лиц с нулевой суммой), продолжающие находить широкое применение в самых различных областях человеческой деятельности (см., например, [24-28] и др.). Существенным преимуществом матричных игр является относительная простота построения математической модели и нахождения (оптимального) решения. Традиционным ограничением является невозможность (в случае антагонистических интересов сторон) практического применения решения в смешанных стратегиях. Отчасти именно этим обстоятельством объясня- ется появление ряда неоклассических постановок матричных игр.
На основе предлагаемой классификации моделируемых ситуаций и порядка интерпретации результатов далее рассмотрены новые возможности поиска детерминированной стратегии позволяющие в определенной степени расширить область практического применения матричных игр.
Матричная игра Г задается тройкой
Г=<Х, Y, Ф> , (1)
где X={x1, x2,..., x,.., x m } - множество стратегий первого игрока; Y={y 1 , у,,.., у,™, yn} - множество стратегий второго игрока; Ф=Ф(xi, у . ) - функция выигрыша первого игрока, Ф = ф ру |, i = 1, m, j = 1, n .
В ходе игры стороны независимо друг от друга выбирают соответственно некоторые чистые стратегии x i е X и у . е Y , в результате чего складывается ситуация (x i , у) . Первая сторона получает выигрыш ф ц , вторая столько же проигрывает. Целью решения игры является нахождение ситуации равновесия, для которой
V = V = V,(2)
min max Ф(x,, у, )=V(З)
yje Y x, е X , max min Ф(x, yj)= V ,
-
x , е X y j e Y
где V - цена игры; V - верхняя цена игры; V -нижняя цена игры.
Решение матричной игры возможно в чистых стратегиях при условии maxmin »i = minmax »i, ijji или в смешанных стратегиях, при условии maxmin Vi ^ minmaxVi.(6)
ijji
Обозначим x и h - смешанные стратегии соответственно первого и второго игрока, тогда m
^ = ( 5 1 , 5 2 ,..., ^ m ), ^ ^ 0, X ^ = 1, (7)
i=1
где x i - вероятность выбора первой стороной чистой стратегии i ;
п = ( п х, П 2 ,-, П п ), 7 , ^ 0, X П = 1, (8)
j =1
где h . - вероятность выбора второй стороной чистой стратегии j .
В существующей литературе классификация матричных игр проводится, как правило, по числу возможных стратегий игроков, а также по их отношению к друг к другу. По первому признаку отдельно выделяют игры размерности 2*2, имеющие арифметическое решение, и игры размерности 2*n (или m*2), допускающие геометрическое решение. По второму – рассматривают различные уровни допустимого риска («благожелательности» соперника) при принятии решения. Это позволяет применять различные критерии для поиска решения, от пессимистического до оптимистического. При условии «равнодушия» соперника к результату матричную игру называют «игрой с природой», и её же без достаточных оснований (в силу соответствия игровой постановки задачам теории статистических решений) отождествляют с так называемой статистической игрой.
Практика показывает, что существующие классификационные признаки матричных игр являются малоинформативными и не способствуют правильной интерпретации полученных результатов. В связи с этим целесообразно применение иной классификации матричных игр. по типу моделируемой ситуации:
-
1) статистические игры;
-
2) игры с природой;
-
3) конфликтные ситуации типа «оборона-нападение»;
2.1. Статистические игры
Покажем принципиальное различие введенных классов матричных игр в плане практической реализации полученных результатов .
Статистической игрой будем называть одношаговую игру двух лиц, имеющих противоположные интересы, целью которой является выбор рациональной стратегии поведения или принятие решения о целесообразности (выгоде) участия на основе полученных статистических оценок. Широко известными в теории игр примерами статистической игры являются игра «в орлянку» и многие достаточно простые карточные игры. Решение в статистических играх находится по максиминному критерию (критерию Вальда) – условие (4). Выбор единственного критерия и является основным отличием статистических игр от игр с природой в предлагаемой авторами классификации матричных игр. Достаточно наглядной иллюстрацией статистической игры является задача «обдираловка» из [29].
Пример № 1 .
У первого игрока (банкующего) имеются три карты: пиковый и трефовый тузы и двойка треф. У вступающего в игру второго игрока также имеются три карты: пиковый и трефовый тузы и пиковая двойка. Игроки откладывают по одной карте и одновременно вскрывают их. При совпадении мастей выигрывает банкующий, в противном случае – второй игрок. При вскрытии двух двоек игра считается ничейной. Требуется определить целесообразность участия в этой игре.
Для определенности будем считать, что при комбинации «туз-двойка» выигрыш равен 2, а при комбинации «туз-туз» равен 1. Матрица выигрышей имеет вид
Вступающий игрок
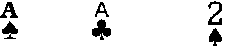
( 1 - 1 - 2
A *

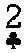
V
-
-
О
>
Рис. 1. Матрица выигрышей карточной игры
Решение игры: £ = ( О; О.6О; О.4О ) , П = ( О.4О; О.6О; О ) , V = О.2О. Следовательно, участие в игре для вступающего игрока будет заведомо невыгодно.
2.2. Игры с природой
Игра с природой в приводимой классификации матричных игр в полной мере соответствует игре с природой, известной в классической теории игр (с той лишь разницей, что теперь она не называется статистической игрой). В постановках таких задач второй игрок («природа») безразличен к выигрышу первого игрока. В большинстве случаев принятие решений на основе модели игры с природой обусловлено неопределенностью действий второго игрока («природы»).
Решение игровой ситуации может осуществляться различными способами, в зависимости от степени информированности о возможных действиях «природы» и от уровня допустимого риска. При этом используются соответственно различные критерии принятия решений:
-
1) критерий Байеса – если известны удовлетворяющие условию (8) значения вероятностей (частот) применения стратегий hj для второго игрока «природа» (например, на основе статистических данных). Тогда по критерию Байеса выбирается стратегия x i * ∈ X , соответствующая максимальному математическому ожиданию выигрыша по условию
∑ n η j ϕ ij ⇒ max ; (9) j = 1
-
2) критерий недостаточного основания Лапласа – при предположении о равной вероятности для любых стратегий игрока «природа», т. е.
∀ j = 1, n - 1 η j = η j + 1, η j ≥ 0, ∑ n η j = 1. (10) j =1
По этому критерию выбирается стратегия,
для которой средневзвешенная сумма элементов платежной матрицы максимальна:
n
Ls>i
—— ^ max; (11)
n
-
3) максиминный (Вальда) критерий - определяет решение игровой ситуации, являющееся гарантирующим, т. е. обеспечивающим минимальный (расчетный) выигрыш при наихудшем стечении обстоятельств. Критерий Вальда, называемый также пессимистическим , задается условием (4) и является основным при нахождении решения матричных игр в общем случае;
-
4) критерий Ходжеса-Лемана , являющийся смесью критериев Байеса и Вальда. Критерий определяет выбор (чистой) стратегии x , е X в соответствии с условием
max | i jr п , Ф , + ( 1 - в ) min Ф , | , (12)
1 ( j = 1 j )
где b е [0, 1] - коэффициент доверия, или реализма.
Достаточно очевидно, что при b =1 критерий (12) превращается в критерий Байеса (9), а при b =0 - в критерий Вальда (4);
-
5) критерий максимума, или оптимистический критерий - определяет выбор стратегии при допущении о максимальной благожелательности игрока «природа» по условию
maxmax ф ( x. - у, ) (13)
-
x , е X у , е Y
-
6) критерий Сэвиджа, или минимаксного риска – обуславливает выбор решения по условию min l max r d , (14)
i V j )
с использованием вспомогательной матрицы риска
R =14 r y = max j ? y v i = 1 m - j = ls n ; (15)
7) критерий пессимизма-оптимизма Гурвица
2.3. Конфликтные ситуации типа «оборона-нападение»
определяется выражением maxi a min ^. + (l - a)max^.
V j j j j где a е [0,1] - коэффициент оптимизма.
Критерий соответствует некоторой промежуточной позиции между ожиданием наихудшего и наилучшего поведения «природы». При a =1 критерий Гурвица превращается в критерий Вальда (4), а при a =0 - в критерий максимума (13).
Достаточно удачный пример использования различных критериев при исследовании игры с природой приводится, в частности, в [30]. Неоклассическим развитием этого класса игр являются соответствующие динамические игры с природой [21].
Универсальным критерием при исследовании игр с природой традиционно является критерий Вальда. Однако невозможность (в большинстве случаев) практической реализации решения игры в смешанных стратегиях определяет растущий интерес к альтернативам максиминного критерия. В свою очередь, применение иных правил нахождения решения требует определенной ответственности от лица, принимающего решение, при выборе конкретных экспертных значений коэффициентов для критериев (12) и (16), или при допущении о возможностях игрока «природа» для критериев (9) и (11). Ошибочность решений на этом этапе может существенно снизить адекватность теоретико-игровой модели и, в конечном итоге, привести к недостоверности полученных результатов.
Матричные игры этого класса, по сути, являются усложнением рассмотренных в п. 2.1 статистических игр. Усложнение относится, прежде всего, к существенному развитию самой игровой ситуации, как правило, имеющей большую размерность, а также к необходимости выбора и практической реализации конкретной (детерминированной) стратегии. Типовым примером игры типа «оборона-нападение» является так называемая «игра полковника Блот-то», впервые сформулированная в [31] и решенная в общей постановке сравнительно недавно [32]. В классическом варианте «игра полковника Блотто» состоит в распределении ограниченных ресурсов («отрядов») по нескольким объектам («полям битв»). Игрок, имеющий наибольшее количество ресурсов на объекте, владеет этим объектом. Требуется найти такое распределение ресурсов по объектам, при котором будет захвачено максимальное количество объектов.
Постановка «игры полковника Блотто», успешно примененная в наше время при организации ряда предвыборных компаний, сегодня переживает второе рождение, дополняясь различными условиями о степени взаимной информированности сторон и приобретая множество самых различных практических приложений [14, 23]. Применительно к классическому дискретному варианту задачи, основными практическими проблемами оставались трудности применения решений в смешанных стратегиях. Следует отметить, что в известной литературе указанной проблеме неизменно уделялось некоторое внимание. Например, в [30] рекомендуется комплексное (одновременное) применение различных образцов вооружения на одном самолете, или различных снарядов к одной пушке. Вместе с тем, авторам так и не удалось избежать результатов решения задач в формате «с вероятностью 0.3 наступать двумя полками, с вероятностью 0.7 наступать тремя полками».
Проведенные исследования показали, что, например, различные комбинации критериев (4), (9) и (11) также не приносят желаемого результата. В частности, в [33] предпринималась попытка применения использующего теорему о минимаксе в матричных играх критерия
∑n ϕijηj m j=n1 ⇒ max. (17)
∑∑ ξ i ϕ ij η j i = 1 j = 1
Рассмотрим более подробно проблему реализации смешанной стратегии в конфликтной ситуации типа «оборона-нападение».
Пример № 2 .
Пусть задана платежная матрица
|
' - 24 |
17 |
33 |
7 ' |
|
2 |
- 22 |
21 |
41 |
|
18 |
12 |
3 |
- 24 |
|
V 31 |
23 |
- 19 |
11 , |
Интерпретация игры может задаваться следующим образом. Первый игрок имеет четыре несовместных варианта проведения воздушной операции с целью поражения объекта. Второй игрок имеет четыре несовместных варианта противодействия воздушной операции, заключающиеся, например, в комплексном использовании средств ПВО, авиации и маскировки. Платежная матрица отражает выгоду при (частичном) поражении объекта, или ущерб при боевых потерях.
Решение игры (полученное, например, с помощью комплекса программ Tora [34]):
§ = ( 0.23; 0.24; 0.26; 0.27 ) ,
П = ( 0.36; 0.17; 0.40; 0.07 ) , V = 8.12.
Обозначим левую часть выражения (17) как Qi . Получим Qm =(0.9655; 1.016; 0.990; 1.006).
Аналогично обозначим
Q * j =
m
∑ξiϕij i =1
mn
∑∑ ξ i ϕ ij η j i = 1 j = 1
и получим Qn =(0.985; 0.980; 1.020; 0.945).
Очевидно, что выбор сторонами чистых стратегий x2 и y3 , соответствующих значениям ξ 2 = 0.24 и η 3 = 0.40, не выглядит рациональным и вообще пригодным. Однако при отсутствии на практике альтернативных стратегий следует делать именно такой выбор, с учетом аналогичных трудностей выбора стратегии действий у соперника.
Наряду с этим, целесообразно попытаться улучшить решение. Для этого могут применяться два альтернативных или взаимно дополняющих друг друга способа:
-
- рассмотрение других возможных стратегий;
-
- целенаправленное улучшение характеристик имеющихся стратегий.
При введении в рассмотрение новых стратегий моделируемая ситуация кардинальным образом изменяется. По сути, осуществляется переход к новой матричной игре, решение которой начинается заново. Подобный подход может иметь существенную практическую значимость, однако в теоретическом плане не представляет каких-либо трудностей и далее не рассматривается.
Целенаправленное улучшение параметров игровой ситуации логично осуществлять на основе применения стратегической рефлексии. Под последней будем понимать процесс и результат размышлений одной стороны (игрока, агента) о том, какие принципы принятия решений использует другая сторона (другой игрок, или агент) в рамках той информированности, которую он им приписывает в результате информационной рефлексии. Соответственно, под информационной рефлексией будем подразумевать процесс и результат размышлений одной стороны (игрока, агента) о том, каковы значения неопределенных параметров, что об этих значениях знает и думает другая сторона (другой игрок, или агент).
Следовательно, информационная рефлексия обычно связана с недостаточной взаимной информированностью сторон (прежде всего - о тех или иных параметрах игровой ситуации), в то время как стратегическая рефлексия имеет место при полной информированности [9].
При целенаправленном улучшении параметров игровой ситуации на основе стратегической рефлексии естественно предположить, что изменяться в первую очередь должны те значения V ij , для которых п j ^ max. Проверим это утверждение экспериментально. Для матрицы примера № 2 будем последовательно изменять элементы V ij на одну и ту же величину и наблюдать изменение основного параметра – цены игры. Значения цены игры при последовательном увеличении элементов v ij сначала на 10, а затем на 30 показаны в табл. 1 в формате V+10 /V+30 .
Полученные экспериментальные данные подтверждают пропорциональную зависимость цены игры от вероятностей (частот) выбора стратегий. Таким образом, действительно, при возможности корректировки своих стратегий следует, в первую очередь, «улучшать» параметры тех элементов v ij стратегий, использование которых наиболее вероятно другой стороной, т. е.
V ij : j = arg(max n j ) . (19)
Вместе с тем, изучение табл. 1 показывает, что различные по модулю или по знаку элементы платежной матрицы v j могут вносить существенно различный вклад в формирование значения цены игры. В рамках исследования соответствующих закономерностей рас-
Таблица 1. Значение цены игры V+10/V+30 при увеличении значений элементов платежной матрицы ϕ ij (выделены значения цены игры при увеличении отрицательных элементов ϕ ij )
|
x i \ y j |
y 1 |
y 2 |
y 3 |
y 4 |
|
x 1 |
9.14/13.35 |
8.47/8.94 |
9.04/10.87 |
8.27/8.54 |
|
x 2 |
8.92/10.26 |
8.62/10.70 |
9.03/10.62 |
8.27/8.52 |
|
x 3 |
8.91/9.94 |
8.63/10.20 |
9.02/10.25 |
8.34/9.58 |
|
x 4 |
9.15/11.82 |
8.54/9.12 |
9.54/15.22 |
8.28/8.52 |
смотрим, например, изменение цены игры при изменении элементов платежной матрицы ф 21 = 2 , ф 23 = 21, ф АХ = 31 и ф ^г =- 19 .
Очевидно, что значение DVij в табл. 2 существенно зависит от значения соответствующей вероятности (частоты) η j . В связи с этим в табл. 2 представлены вариации значений различных по модулю элементов матрицы ф 21 и ф 41 из одного столбца. Аналогично различные по знаку, но близкие по модулю элементы матрицы ф 23 и ф 43 также взяты из одного столбца. В целом анализ таблиц 1 и 2 позволяет сделать следующие утверждения (для матричных игр).
Утверждение 1 . Изменение положительного элемента платежной матрицы с большим модулем приводит к более существенному изменению значения цены игры.
Утверждение 2. Увеличение отрицательного элемента платежной матрицы приводит к большему увеличению цены игры, чем уве- личение положительного элемента платежной матрицы (при одинаковых модулях этих чисел).
Таким образом, при исследовании конфликтной ситуации типа «оборона-нападение» при наличии решения в смешанных стратегиях, в котором сложно выделить предпочтительную стратегию, целесообразно целенаправленное улучшение своих стратегий в соответствии со следующими правилами:
1) следует улучшать возможности действий, приводящие к увеличению таких элементов платежной матрицы, для которых вероятность (частота) их выбора противником максимальна (условие (19));
2) при возможности выбора различных вариантов своих действий, приводящих к увеличению различных положительных элементов платежной матрицы (при выполнении условия (19)) следует стремиться к увеличению наибольшего элемента платежной матрицы;
3) при возможности выбора различных ва-
Таблица 2. Значение цены игры при вариации элементов ф21, ф23, ф41 и ф43
№
п/п
ф21
V
ΔV21
ф41
V
ΔV41
ф23
V
ΔV23
ф43
V
ΔV43
1
-8
7.22
-0.90
21
7.18
-0.94
11
7.12
-1.00
-29
7.21
-0.91
2
-7
7.31
-0.81
22
7.27
-0.85
12
7.22
-0.90
-28
7.28
-0.84
3
-6
7.41
-0.71
23
7.36
-0.76
13
7.33
-0.79
-27
7.37
-0.75
4
-5
7.50
-0.62
24
7.46
-0.66
14
7.43
-0.69
-26
7.45
-0.67
5
-4
7.59
-0.53
25
7.55
-0.57
15
7.53
-0.59
-25
7.53
-0.59
6
-3
7.68
-0.44
26
7.64
-0.48
16
7.63
-0.49
-24
7.62
-0.50
7
-2
7.77
-0.35
27
7.74
-0.38
17
7.73
-0.39
-23
7.71
-0.41
8
-1
7.86
-0.26
28
7.83
-0.29
18
7.83
-0.29
-22
7.81
-0.31
9
0
7.91
-0.17
29
7.93
-0.19
19
7.93
-0.19
-21
7.91
-0.21
10
1
8.04
-0.08
30
8.02
-0.10
20
8.03
-0.09
-20
8.01
-0.11
11
2
8.12
0
31
8.12
0
21
8.12
0
-19
8.12
0
12
3
8.21
0.09
32
8.22
0.10
22
8.22
0.10
-18
8.23
0.11
13
4
8.29
0.17
33
8.32
0.20
23
8.31
0.19
-17
8.35
0.23
14
5
8.37
0.25
34
8.42
0.30
24
8.40
0.28
-16
8.48
0.36
15
6
8.45
0.33
35
8.52
0.40
25
8.50
0.38
-15
8.61
0.49
16
7
8.53
0.41
36
8.62
0.50
26
8.59
0.47
-14
8.74
0.62
17
8
8.61
0.49
37
8.73
0.61
27
8.68
0.56
-13
8.89
0.77
18
9
8.69
0.57
38
8.83
0.71
28
8.77
0.65
-12
9.04
0.92
19
10
8.77
0.65
39
8.94
0.82
29
8.86
0.74
-11
9.19
1.07
20
11
8.84
0.72
40
9.04
0.92
30
8.94
0.82
-10
9.36
1.24
21
12
8.92
0.80
41
9.15
1.03
31
9.03
0.91
-9
9.54
1.42
3. МЕТОДЫ РЕШЕНИЯ МАТРИЧНЫХ ИГР
риантов своих действий, приводящих к увеличению различных, в том числе отрицательных, элементов платежной матрицы (при выполнении условия (19)), следует стремиться к увеличению элементов платежной матрицы, имеющих отрицательные значения (наибольших по модулю среди элементов матрицы с отрицательными значениями).
Рассмотрим применение сформулированных правил на примере № 2. В соответствии с первым правилом (условие (19)) следует изменять элементы платежной матрицы из третьего столбца. На практике это означает стремление к приоритетному ослаблению наиболее опасной стратегии противника.
По третьему правилу при наличии в столбце элементов с отрицательными значениями следует стремиться к увеличению, прежде всего, именно этих элементов. В примере № 2 таким элементом является ф 43 =- 19 . Отрицательный элемент ф ij (наибольший по модулю среди элементов матрицы с отрицательными значениями) платежной матрицы в столбце, удовлетворяющем условию (19), соответствует, по сути, наиболее неблагоприятной для нас ситуации при выборе противником стратегии у . е Y в ответ на нашу стратегию xt е X .
Предположим, нам удалось целенаправленно улучшить свою стратегию x4 таким образом, что значение Ф 43 стало равняться -2. Решение игры при этом существенно изменится и станет равным £ = ( 0.24; 0.22; 0; 0.54), П = ( 0.36; 0.06; 0; 0.58 ) , V = 11.46.
В результате корректировки стратегии x4 цена игры заметно возросла, а основная стратегия y3 утратила актуальность. В то же время стратегия x4 стала более привлекательной.
Подобное «улучшение» стратегий, в совокупности с моделированием новых игровых ситуаций на основе рассмотрения новых стратегий, по всей видимости, является наиболее перспективным направлением практического применения матричных игр для исследования конфликтных ситуаций типа «оборона-нападение».
Матричные игры имеют хорошо апробированные на практике методы решения. Универсальным методом решения матричной игры является сведение её к задаче линейного программирования. Вместе с тем, для матричных игр размерностей 2*2 и 2*n (или m*2 ) существуют более простые методы решения. В частности, решение матричных игр размерности 2*2 находится по арифметическим формулам
^ = ^ 22 - Ф 21
1 Ф 11 + ^ 22 - Ф 12 - Ф 21 '
е ______ Фи ф12 _____
Ъ 2 = ,
Ф 11 + Ф 22 - Ф 12 - Ф 21
п = Ф 22 - Ф 12
-
1 Ф 11 + Ф 22 - Ф 12 - Ф 21 ,
% = 1 - %,
V = Ф 11 Ф 22 - Ф 12 Ф 21
Ф 11 + Ф 22 - Ф 12 - Ф 21
Общеизвестным также является геометрическое решение матричных игр размерности 2*n (или m*2 ).
При решении матричных игр путём сведения их к задачам линейного программирования на основе платежной матрицы ф = Ц ф . ^ Ц формулируется пара взаимосопряженных задач
|
m X^^i> v , i = 1 i |
||
|
m X t = 1, i = 1 |
и |
(25) |
Й > 0
n
X ФП ^ v j=1 ij j
n
X n j = 1, [ .
j = 1
n j > 0.
Решение задач (25) и (26) позволяет получить значения вероятностей выбора смешанных стратегий и цены игры, равной, в силу основной теоремы теории игр, совпадающим экстремумам целевых функций Ф(xi, yj) и -Ф(xi, yj) . Применение методов решения задач линейного программирования (например, симплексного метода и его модификаций) на сегодняшний день существенно упрощено наличием комплексов специализированных программных средств, например, комплекса программ Tora [34].
Вместе с тем, во многих практических ситуациях не требуется получения точного решения игры, а достаточно приближенных значений. Наиболее целесообразным применение итеративных методов решения матричной игры становится для задач размерности 103≤( m * n )≤106, так как с ростом числа возможных стратегий m и n объем вычислений при решении задач (25) и (26) стремительно (например, экспоненциально для симплексного метода) возрастает.
Одним из наиболее простых в плане наглядности и практической реализации для решения матричных игр является обладающий приемлемой сходимостью итеративный метод Брауна-Робинсон, впервые сформулированный в [35]. Идея метода основана на построении одной из сторон конфликтной ситуации гипотетической последовательности партий, с учётом опыта розыгрыша всех предшествующих фиктивных партий. После проведения ряда итераций относительные частоты применения чистых стра- тегий приближенно можно принять в качестве оптимальных смешанных стратегий участников конфликта, а средний выигрыш является приближенным значением цены игры.
Поиск итеративного решения матричной игры основан на расчетных соотношениях
Известная априорная оценка 5 s ) погрешности решения (цены игры) в зависимости от числа итераций [36]
^ S ) = S n + m - 2 (32)
R S + 1 )= R^ ) + V j , (27)
|
R S + 1 )= R S ’ + ф 1 в , |
(28) |
|
min RS) |
|
|
. S j |
(29) |
|
L = s ’ |
|
|
V S ) max R S1 |
(30) |
|
S ’ |
|
|
v(S) 4_vS V ( S ) V + V |
(31) |
|
2 ’ |
является слишком грубой. Сложность получения хороших теоретических оценок погрешности метода обусловлена существенной зависимостью априорной оценки от элементов платежной матрицы. Вместе с тем, в [37] доказана пригодность (см. рис. 2 и 3) практического использования значения погрешности 5 s , вы-
числяемого непосредственно в ходе итератив-
ного процесса по формуле
5 s =
и
где 3 - номер итерации (номер партии игры); R1j – суммарный выигрыш при применении стратегии xt Е X ; R2i - суммарный проигрыш при использовании стратегии у Е Y .
Основной проблемой на практике является определение достаточного количества итераций для достижения требуемой точности результата.
V S ) - V S
V S + v S)'
Примем V 3 ) - V 3 ) = а V ( 3 ) . Тогда
5 S ) = и
а V ( 3 )
2 V ( 3 ) .
Предложенная оценка (34) погрешности результата для итеративного метода Брауна-
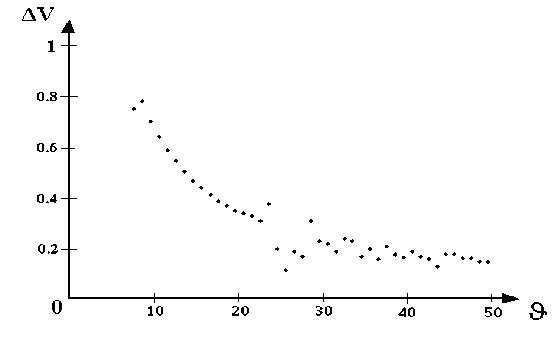
Рис. 2. Изменение значения а ^ в ходе итеративного процесса (для матрицы размерности 3*3)
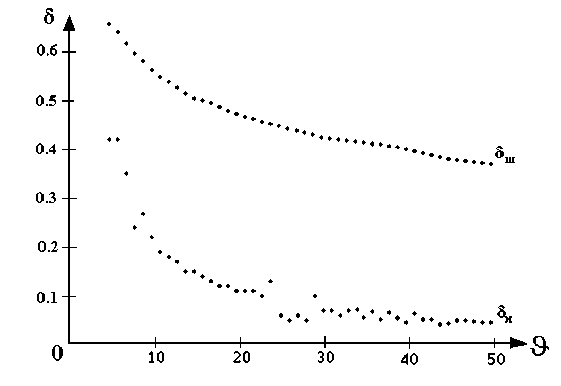
Рис. 3. Изменение значений априорной 5 s ) и апостериорной 5 s ) оценок погрешности результата в зависимости от количества итераций (для матрицы размерности 3*3)
Робинсон существенно повышает привлекательность практического применения метода. Вместе с тем современные задачи, являющиеся предметом исследования матричных игр, в ряде случаев могут иметь размерность ( m * n )>106. Для подобных задач разрабатываются новые методы поиска решения, по-прежнему основанные на применении итеративных процедур [38, 39].
ЗАКЛЮЧЕНИЕ
Появление и развитие новых направлений современной теории игр стимулируется практическими потребностями решения принципиально новых задач, характерных для объектов междисциплинарной природы. Вместе с тем дальнейшее существенное усложнение теоретико-игровых постановок усугубляет известные теоретические трудности как адекватной формализации исследуемых процессов, так и поиска решения в ситуациях с множеством равновесных ситуаций, характерных, в частности, для некоалиционных игр. В этой связи растет актуальность разработки общих подходов для исследования сложных игровых моделей на основе различных методов их декомпозиции, в частности – путем разбиения на совокупность взаимосвязанных более простых игр, вплоть до матричных (биматричных). Однако матричные игры исторически имеют свои известные особенности, заметно ограничивающие область их практического применения. В статье предложена новая классификация матричных игр и некоторые оригинальные методические приемы, позволяющие расширить границы использования результатов решения матричных игр на практике.
Список литературы Стратегическая рефлексия в матричных играх
- Губанов Д.А., Новиков Д.А., Чхартишвили А.Г. Социальные сети: модели информационного влияния, управления и противоборства . М.: Издательство физико-математической литературы, 2010. 228 с.
- Michalak T., Rahwan T., Skibski O., Wooldridge M. Defeating Terrorist Networks with Game Theory//IEEE Intelligent Systems, vol. 30, no. 1, 2015, pp. 53-61.
- Торопов Б.А., Тагиров З.И. Модели террористических сетей и теоретико-игровой подход к оценке центральности их участников//Вопросы безопасности. 2016. № 6. С. 77-89.
- Weibull J. Evolutionary Game Theory. Cambridge: MIT Press, 1995.
- Васин А.А. Некооперативные игры в природе и обществе. М.: МАКС Пресс. 2005. 412 с.
- Suriya Sh. Kumacheva, Elena A. Gubar. Evolutionary model of tax auditing//Contributions to Game Theory and Management, 2015, Volume 8, 164-175.
- Wang, Min. Mathematical and statistical models in evolutionary game theory, 2015, Graduate Theses and Dissertations, 14449. URL: http://lib.dr.iastate.edu/etd/14449 (дата обращения 15.04.2017)
- Новиков Д.А. Модели стратегической рефлексии//Автоматика и телемеханика. 2012. № 1. С. 3 -18.
- Новиков Д.А., Чхартишвили А.Г. Рефлексия и управление: математические модели. М.: Издательство физико-математической литературы. 2013. 412 с.
- Algorithmic Game Theory/Eds. Nisan N., Roughgarden T., Tardos E., and Vazirani V. N.Y.: Cambridge University Press, 2009. 776 p.
- Mansour Y. Computational Game Theory. Tel Aviv: Tel Aviv University, 2003. 150 p.
- Robert Adkins. Algorithmic Game Theory. Final Report for CMSC451 Honors Option. Fall 2015, 13 p.
- Roth A.E. Game Theory as a Tool for Market Design. Game Practice//Contributions from Applied Game Theory. Theory and Decision Library. 2000. Vol. 23. P. 7-18. ( ) DOI: 10.1007/978-1-4615-4627-6_2
- Горяшко А.П. Теория игр: от анализа к синтезу. Обзор результатов//Электронный журнал Cloud of Science. 2014. T. 1. № 1. С. 112-154. URL: http://cloudofscience.ru (дата обращения 15.04.2017).
- Dechenaux E., Kovenock D., Sheremeta R.M. A Survey of Experimental Research on Contests, All-Pay Auctions and Tournaments//Experimental Economics. 2015. Vol. 18, No. 4. P. 609-669.
- Bocharov P., Goryashko A., Nikulchev E.V. Partition Games as Contests: Numerical Simulation Results//Applied Mathematical Sciences. 2015. Vol. 9, No. 104. P. 5149-5167.
- Шубик Мартин. Настоящее и будущее теории игр//Математическая теория игр и ее приложения. 2012. Т. 4. № 1. С. 93-116.
- Widger J. and Grosu D. Computing Equilibria in Bimatrix Games by Parallel Support Enumeration. In Proceedings of the 2008 international Symposium on Parallel and Distributed Computing (July 01-05, 2008). ISPDC. IEEE Computer Society. Washington, DC, 2008. Р. 250-256.
- Нестеренко М.Ю., Кириллов А.С. Разработка и анализ высокопроизводительного параллельного алгоритма решения кооперативных игр сведением к биматричным играм//Бюллетень Оренбургского научного центра УрО РАН (электронный журнал). 2014. № 2.
- Данилов Н.Н. Динамические матричные игры. Обоснование применения принципа минимакса в классе чистых комбинированных стратегий//Вестник КемГУ. 2012. № 2 (50). С. 42-48.
- Данилов Н.Н. Математическая модель менеджмента в условиях неопределенности в форме динамической игры с природой//Вестник КемГУ. 2012. № 3 (51). С. 110-114.
- Сигал А.В. Игровые модели принятия решений с учетом риска//Проблемы анализа риска. 2012. Т. 9. № 4. С. 54-64.
- Корепанов В.О., Новиков Д.А. Рефлексивная игра полковника Блотто//Системы управления и информационные технологии. № 47 (1). 2012. С. 55-62.
- Берднова Е.В., Корсунов В.П., Самышин А.В. Математическое моделирование продуктов питания для здорового образа жизни методом матричного структурирования//Аграрный научный журнал. 2016. № 2. С. 44-47.
- Калиниченко Е.Ф., Кузнецова С.А., Ярыш В.А. Матричные игры//Комплексные проблемы развития науки, образования и экономики региона. 2012. № 1. С. 161-166.
- Малолетко А.Н., Малолетко Н.Е. Обеспечение экономической безопасности предприятий гостиничного бизнеса с применением теории игр//Инновационное развитие экономики. 2013. № 6 (17). С. 121-124.
- Павлова Т. А., Уварова М.Н. Матричные игры как метод решения экономических задач//Ресурсосберегающие технологии при хранении и переработке сельскохозяйственной продукции. 2016. С. 38-42.
- Пуртов А.М., Чанышев О.Г. Имитация матричных игр как метод анализа практических стратегий принятия решения//Омский научный вестник. 2013. № 1 (117). С. 229-233.
- Гасс С. Путешествие в Страну Линейного программирования. М.: Мир. 1971. 176 с.
- Вентцель Е.С. Исследование операций. М.: Советское радио, 1972. 00552 с.
- Borel E. La theorie du jeu les equations integrales a noyau symetrique. // Computes Rendus del Academie. 1921. Vol. 173. No.19. P. 1304-1308 (English translation by Savage L.: The Theory of Play and Integral Equations with Skew Symmetric Kernels // Econometrica, 1953. Vol. 21. No. 1. P. 97-100.
- Roberson B. The Colonel Blotto game//Economic Theory. 2006. Vol. 29. No. 1. P. 1-24. ( ) DOI: 10.1007/s00199-005-0071-5
- Воробьев А.А. Теоретико-игровой подход к оцениванию качества системы защиты информации от несанкционированного доступа в автоматизированных системах//Информатика -машиностроение. 1999. № 3. С. 12-17.
- Таха Хемди А. Введение в исследование операций. М.: Издательский дом «Вильямс». 2005. 912 с.
- Brown G.W. Iterative Solutions of games by fictitious play, Activity Analisys of Production and Allocation, ed. By Koopmans, Cowles Commission for Research in Economics Monograph, №13, Wiley, New York, 1951.
- Shapiro H.N. Note on a computation method in the theory of games. Comm. Pure and Appl. Math. 11, 4, 1958.
- Воробьев А.А. Практические методы принятия решений в конфликтных ситуациях с неполной информацией//Информатика -машиностроение. 1999. № 4. С. 22-25.
- Зубов А.Ю. Решение некоторых классов матричных игр//Прикладная дискретная математика. 2016. № 4 (34). С. 17-37.
- Чижонков Е.В. Многоуровневый метод решения больших матричных игр//Вычислительные методы и программирование. 2009. Т. 10. С. 327-339.


