Strongly continuous operator semigroups. Alternative approach
Бесплатный доступ
Inheriting and continuing the tradition, dating back to the Hill-Iosida-Feller-Phillips-Miyadera theorem, the new way of construction of the approximations for strongly continuous operator semigroups with kernels is suggested in this paper in the framework of the Sobolev type equations theory, which experiences an epoch of blossoming. We introduce the concept of relatively radial operator, containing condition in the form of estimates for the derivatives of the relative resolvent, the existence of C 0-semigroup on some subspace of the original space is shown, the sufficient conditions of its coincidence with the whole space are given. The results are very useful in numerical study of different nonclassical mathematical models considered in the framework of the theory of the first order Sobolev type equations, and also to spread the ideas and methods to the higher order Sobolev type equations.
Sobolev type equation, strongly continuous semigroups of operators with kernals, approximations of semigroups
Короткий адрес: https://sciup.org/147159210
IDR: 147159210
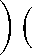
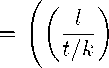
Список литературы Strongly continuous operator semigroups. Alternative approach
- Хилле, Э. Функциональный анализ и полугруппы/Э. Хилле, Р. Филлипс. -М.: ИЛ, 1962.
- Sviridyuk, G.A. Linear Sobolev Type Equations and Degenerate Semigroups of Operators/G.A. Sviridyuk, V.E. Fedorov. -Utrecht; Boston; Köln; Tokyo: VSP, 2003.
- Demidenko, G.V. Partial Differential Equations and Systems not Solvable with Respect to the Highest Order Derivative/G.V. Demidenko, S.V. Uspenskii. -N.Y.; Basel; Hong Kong: Marcel Dekker, Inc., 2003.
- Favini, A. Degenerate Differential Equations in Banach Spaces/A. Favini, A. Yagi. -N.Y.; Basel; Hong Kong: Marcel Dekker, Inc., 1999.
- Lyapunov-Schmidt Methods in Nonlinear Analysis and Applications/N. Sidorov, B. Loginov, A. Sinithyn, M. Falaleev. -Dordrecht; Boston; London: Kluwer Academic Publishers, 2002.
- Al'shin, A.B. Blow-up in Nonlinear Sobolev Type Equations/A.B. Al'shin, M.O. Korpusov, A.G. Sveshnikov. -Series in nonlinear analisys and applications, 15, De Gruyter, 2011.
- Свиридюк, Г.А. Линейные уравнения типа Соболева и сильно непрерывные полугруппы разрешающих операторов с ядрами/Г.А. Свиридюк//ДАН. -1994. -Т. 337, № 5. -С. 581-584.
- Sviridyuk, G.A. The Phase Spaces of a Class of Linear Higher-order Sobolev Type Equations/G.A. Sviridyuk, A.A. Zamyshlyaeva//Differential Equations. -2006. -V. 42, № 2. -P. 269-278.
