Structural Identification of Dynamic Systems with Hysteresis

Published Online July 2016 in MECS DOI: 10.5815/ijisa.2016.07.01

The problem of structural identification occupies one of the basic places in control theory. In the theory of parametric identification considerable results are received. Research in the domain of structural identification demands the further advancing. The problem has not obtained the final decision. Such condition of the problem structural identification (SI) explains complexity of mathematical statement the problem and lack of regular methods of its solution. The majority of approaches to SI are grounded on search of models from the give set or approximation of a nonlinear part system on the class of polynomials. The basis of the specified approaches is parametric identification.

Methods of an estimation structure are widely applied to the systems described by integral equations of Wiener and Wiener-Hammerstein. In [1] structure of model is set a priori. Nonlinearity is described by polynomial function of the second order. Basic virtues of Wiener and Wiener-Hammerstein models: (i) transformation of models to the regression form; (ii) application of parametric methods identification for their construction. Application Wiener and Wiener-Hammerstein models is given in [2]. Authors consider the a priori information on nonlinearity framework. The piecewise-linear approximation is applied to the nonlinearity description. Different approaches to identification of nonlinear plants on the basis of Wiener and Wiener-Hammerstein models are considered in [3, 4].

In the review [5] is given the analysis of the condition problem identification nonlinear processes in structural dynamics. Many nonlinear processes in a structural dynamics are described by the equations with a hysteresis. Time and frequency methods of parametric identification are considered. Methods of an estimation of type nonlinearity are analyzed. Different physical and frequency methods, and procedures for handling results of an experiment are used for the construction of parametric models. Typical methods, applicable for studied subject domain, are considered in review. Methods of the correlation analysis [6] and error localization in a linear model updating framework [7, 8], and also pattern recognitions [9] were applied to an estimation of type nonlinearity. The problem of an estimation of type nonlinearity solves on the class of the specified models. The problem of a choice the dependence describing nonlinearity is considered. Application of polynomial approximation the initial stage in the presence of the a priori information is justified. The choice of the order polynomial is the main problem of this approach. Criteria and algorithms of an estimation of an order polynomial are considered. They are based on the calculation of the significance factor [10] and the coherence function [11]. Shortages of such approach are noted. The models received by means of these approaches, not always adequately describe examined processes. In [12] Bayesian approach is applied to the estimation of the polynomial order. In [5] limitation of the polynomial approach is noted. Models does not allow describing the wide class of nonlinearities.

The role of the a priori information at structure choice is noted in [5]. If the a priori information is insufficient, and the physical model does not reflect the essence of processes, then apply the concept of "black box» [13, 14] and methods of parametric identification.

Nonlinear Hammerstein-type neural network model in

• [15]    is applied to identification of nonlinear system. The Lipschitz criterion is used for estimation an order of system. Algorithms of adjustment weights a network are offered.

A considerable quantity of publications is devoted identification of systems with a hysteresis (look, e.g. [1618]). The Bouc-Wen model (BW) is widely applied to hysteresis description. Various parametric models, approximating parameters of the hysteresis, are considered in [16-18]. In [16] is offered the variant Volterra/Wiener Neural Network model for an estimation of parameters the hysteresis of dynamic system the second order. The model is described by the regression equation. The adaptive algorithm is offered for identification of parameters the equation.

In [17] models for approximation of a symmetric and asymmetrical hysteresis with use of piecewise-linear functions are considered. The model is described by a discrete difference equation of first order. Iterative procedure is offered for an estimation of the model parameters. The system of the second order with the hysteresis described by BW model is considered in [18]. Modification of the self-adjusted differential evolutionary algorithm for the estimation of the hysteresis parameters is proposed. Approaches to the parametric identification hysteresis, which is described by various nonlinear functions, are considered in [19-21].

Except the Bouc-Wen model other dependences are applied to hysteresis description. Examples of the parametric identification such models of a hysteresis are considered in [see for example 22-24].

So, the analysis of publications shows that the problem of structural identification systems with the hysteresis demands the further study. Now the main direction of researches is various methods of approximation nonlinearity and the account of a priori information. The proposed methods are based on the application of parametric identification procedures. Some authors examined problems of structural identification (choice forms of nonlinear function, nonlinearity type) for plants with the known class of nonlinearity. These inferences are fair for systems with the hysteresis. The main difficulty of identification a hysteresis in the conditions of uncertainty is the lack of methods of obtaining the a specific information. This information reflects nonlinear properties of the system. Such condition of the theory identification we explain the prevalence of methods approximation. But the main tasks of structural identification, despite the effectiveness of application such schemes in several of applications, remains unsolved. First unsolved problem is the estimate of the form (type) nonlinearity. Approaches to its solution in the conditions of a priori uncertainty were not offered. The second problem is the estimation of a class of nonlinearity. It is class single-valued or multi- valued functions. The solution of this problem gives a contraction of the class considered nonlinearity. The third problem is obtaining of preliminary representation about a form of nonlinearity (hysteresis) in the conditions of uncertainty.

In this work, we offer methodology of structural identification dynamic systems with the hysteresis in the conditions of uncertainty. It is based on the analysis of virtual structures S . S are offered in [25, 26] for structural identification of static systems. Here we give the development and generalization of the obtained results on the dynamic system. S -structures of dynamic systems, unlike statics systems are closed character. S is a transformation of a phase portrait of system. We describe the method of construction S . The method of obtaining the set containing the information on nonlinear properties of system is offered. This set is the basis for construction of the structure S or its transformation S . We introduce ey                                        e the concept h -identifiability system. h -identifiability gives conditions of the estimation framework hysteresis on the basis of the analysis S . We offer algorithms of estimation the structural parameters of the hysteresis. They are based on the analysis S -structure. If system complicated we search for hysteresis parameters, analyzing framework S . S is a transformation of structure S . We proposed structurally-frequency method for verification of the results. Modification of the proposed approach for unstable systems with the dynamic law of a change of a hysteresis is considered.

The work has the following structure. We gives the problem statement and stages of its solution in section II. The first stage is obtaining of the special set containing the data about a nonlinear part of system. The method of construction the set is described in section III. This set is the basis for the formation of structures S , S . They ey     e are the basis of the problem solution about a class of nonlinearity system. The method of construction these structures is described in section IV. The introduction of these structures is associated with the solution of problem structural identifiability of nonlinear systems. This concept is first introduced in this paper. Consideration of structural identifiability is given in section V. Sections VI, VII contain the main results of work. We describe algorithms for decision making about a hysteresis class. They are based on application of sector sets and secant method. Next, we describe of an estimation procedure of the hysteresis framework. Results of modeling are presented. The structurally-frequency method is proposed for decision-making about a hysteresis framework in the conditions of uncertainty. Next we consider SI of an unstable system with a dynamic hysteresis.

• II.    Problem Statement

Consider dynamic system

X = AX + ^ ( y ) I + Bu y = C^TX ,

where u g R , y g R are input and output system; A g R q ^x q , B g R q , I g R q C g R^q ; ф (y ) is the scalar nonlinear function belonging to the class of the hysteresis F_h ; I = [0,0,... ,0,1] ^T . We suppose that A is the Hurwitz matrix.

Concerning function structure % = ф (y ) various assumptions made. They are determined by the level of a priori information. Methods of linearization [27] apply at a priori definiteness. In the study of absolute stability of nonlinear systems suppose that [28]

%g F ^ ( § ) § >  § ², § * 0, ^ (0) = 0 } , (2)

where § g R is input of a nonlinear element. § is a linear combination of the state variables (the vector X ).

For approximation of function % is used the sector condition

% G F = {Y1§ < ^(§)§ < ?2§\ § * 0, ^(0) = 0, y > 0, Y < ^}.

In control systems often apply static nonlinearity. Therefore next we consider the class of the static (algebraic) functions describing a hysteresis.

Let for system (1) we have set of the data

I o = { u^(t ), y ⁽ t X t G J = [ t 0 , t_k ] } .            (4)

Problem: determine a form and parameters of function ^ ( y ) g F on the basis of the analysis and handling of set I o (4).

To the problem solution apply the approach proposed in [25]. Realize following steps.

• 1.    Generate the set I containing the data about a nonlinear part of system (3).

• 2.    Analyze I and construct structure S reflecting properties of the nonlinear part of system.

• 3.    Design algorithm of decision-making about the class of nonlinearity F on the basis of the analysis S _ey .

• 4.    Design procedures of an estimation parameters nonlinearity on class F .

Go to the first step of solving the problem of structural identification. Apply the approach offered in [29].

• III.    Formation of Set I

We present a method of formation set I . This set is a basis for the further analysis of framework a hysteresis.

Apply to y ( t ) the operation of differentiation and designate the obtained variable as x . Generate information^al set I ent = { I o , x 1} .

Remark 1. If variables u , y are measured with an error at first apply filtering or smoothing procedure.

Select the subset of the data I _gc I_ent describing the particular solution of system (1) (steady state).

To obtaining I = I^ XI^ apply mathematical model x\ (t) = HT [1 u(t) y(t)]T.              (5)

Model (5) is determined on the time gap J_g = J X J_tr and gives an estimation of the linear component x . Here H g R ³ is the vector of parameters model. Choice of an interval J depends on value of criterion Q ( e ).

Determine the vector H as min Q(e)  4   ^ Hnn.,

H      \ 7 | e=;x| -x1          opt ’ where Q(e) = 0.5e2.

Apply model (5) and determine the forecast for the variable x ₁ ( t ) V t g I . Compute an error e(t ) = x_x'(t ) - x_x ( t ). e ( t ) depends on nonlinearity ^ ( y ) in system (1). Obtain set

IN,g ={у(t), e(t), t G Jg } , which we will use next. Apply the designation y(t), supposing that y(t) g In,g .

The further solution of the problem is based on the analysis of structures S , S , reflecting the state of the nonlinear part of the system (1).

Remark 2. Choice of the structure model (5) is one of the stages of structural identification. Results of simulation show that model (5) is applicable in systems of identification plants with static nonlinearity. For other classes of nonlinearity, this problem demands the further research. We suppose such approach in section VII.С.

• IV.    Structures S , S

ey     ek

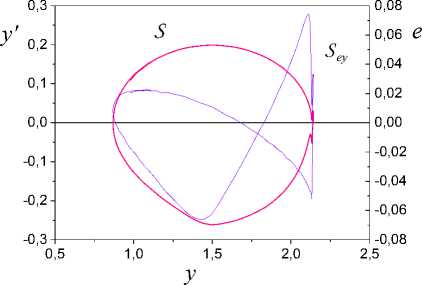
Go into space P = ( y , e ) and construct the phase portrait S of the system (1). The structure S corresponds to the phase portrait. S is described function

Г : { У } ^ { e} V t g J_g . S can have a closed form. The property of closure trajectories S is the main difference S from the frameworks applied to the analysis of static systems [25, 29].

For decision making, we will use also S -structure. SEk is described by function Гек : {ks (t)} ^ {e(t)} , where ks (t) g R is a coefficient of structural properties [25, 29] systems (1) in space P ks (t) = 7..

y ( t )

Generalize results of work [30] which were applied to structural identification of static systems. The obtained results are the basis for the realization of the next stage solving the problem.

We construct sector sets in space P_k = ( k , e ) for system (1) and we will be a make a decision about the class F . The solution of this problem is based on the analysis of property proposed above structures. But at first, study properties of the set I , defining structural identifiability of the system (1). Next consider implementation of the third stage of the solution the problem.

• V.    About Properties I

We will determine the properties of set I giving the solution of the problem structural identification of a hysteresis ^ ( y ). The analysis I_{w g} determines the important property of the informational set I defining a possibility of fulfillment structural identification of nonlinear system (1).

Let following conditions are satisfied:

• 1)    the set I gives the solution of the problem parametric identification of model (5). It means that the input u ( t ) is extreme non-degenerate on the interval J ;

• 2)    the input u ( t ) ensures obtaining of informative frameworks S ey ( I N , _g ) or S ek ( I N , _g ) . It means that the analysis S gives the problem solution of estimation nonlinear properties the system (1).

Input u(t) name representative if it has these proper- ties.

Let the structure S is closed and its area is not zero.

Designate altitude S^ as h (S^) where the altitude is distance between two points of the opposite sides of structure S .

Statement 1. Let: 1) the linear part of system (1) is stable, and nonlinearity p (y ) satisfies the condition (3); 2) the input u ( t ) is piecewise continuous, limited and extremely non-degenerate; 3) exists such # _s >  0 that h ( S ey ) >  5_S . Then the structure S is identified on set I .

Proof. Consider input u ( t ) satisfying to the condition 1). u ( t ) corresponds Fourier series containing a sinusoid of frequency с ц. . The output y ( t ) g I_w contains components of this spectrum and has phase shift rather u ( t ). The variable x is obtained as a result of derivation y ( t ). Hence, x contains components of this frequent spectrum. Therefore, the structure S (phase portrait) on the phase plane ( y , x ) has a closed form. The S_E -structure has the same form. Determine the distance h ( S^ ) between opposite points of the structure S . y ( t ), x ( t ) satisfy the condition 2) statement 1. Therefore, for almost all t ^{g J}n , g ^h ( S ey ) > ⁵ s .

The structure S having the specified properties, we will name h -identified. Further, we believe that S has the specified properties.

Consider the features of the concept h -identifiability.

• 1.    h -identifiability is concept not parametric identification, and structural identification.

• 2.    The demand of parametric identifiability is the base h -identifiability.

• 3.    h -identifiability sets more stringent demands to the system input.

The feature 3 means that "the bad" input can satisfy to the extreme nondegenerate condition. Such input can give so-called "insignificant" S -structure (structure NS ). But NS -structure can have to be h -identified. Property of insignificance in the conditions of uncertainty can lead to an identification of nonlinearity, atypical for examined system.

Consider the conditions of existence NS -structure.

As we consider the class F hysteresis functions to them homothety operation is applicable. The homothety [31] is the operation of obtaining one part of a geometrical figure from another part on the basis of its rotation and extension around a certain point on a plane ( y , e ) .

Consider the structure S^, . Let S„,, = Fl и FГ , where ey             ey       S _ey        S _ey

F^l , F^r are left and right fragments S . Determine for S ey     S ey                                                             ey

F^l , F^r secants

S ey     S ey

Y s = a‘y Y S = a^ry ,              (6)

where a^l , a^r are the numbers determined by means of the method of least squares (LSM).

Theorem 1. Let: 1) the structure S is h -identifiable; 2) the structure S, have the form S_, = F l u F , where ey                                ey        S _ey         S _ey

Fl,Fr are left and right fragments S ; 3) for Fl,Fr Sey    Sey                                                           ey                   Sey    Sey secants (6) are obtained. Then S is NS -structure, if

| al - ar| > §h, where ^ > 0 is some number.

The proof of the theorem 1 like the proof of statement from [30] and is based on application of the homothety and sector sets. Next we will consider the example illustrating a emersion NS -structures.

Remark 3. Theorem 1 can be proved on the basis of ho-mothety sets. Estimate in this case proximity of sets F_S^l , F_S^r . The approach based on secant method, is more simple in realization.

Remark 4. NS -structures are characteristic for systems with many-valued nonlinearities. They are the result of inadequate use of inputs.

Definition 1. If the structure S is h -identified and the condition | a^r - a^r | <  ^ is satisfied, then S^ is structurally identified or h -identified.

Go now to an estimation of the class nonlinearity , ( y ). This is one of the main tasks of structural identification.

• VI. Estimation of Class Nonlinearity , ( y )

Consider classes of single-valued F and many-valued F nonlinearity. These classes contain the set of nonlinear functions. We propose criteria and indexes for a definition of a subset of these classes. We apply obtained result to decision making about a class of nonlinearity function ; (y ) in (1).

Fragment of structure S for the estimation of the class nonlinearity ,(y) on the basis of analysis subset I c I^  . I adequately reflects the change of the func tion % = ,(y) in structural space Pe.

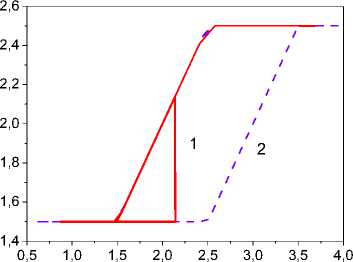
The problem of obtaining the subset I is nontrivial and depends on the available a priori information [29]. In the conditions of uncertainty, it is reduced to a selection of a variation interval the variable y e I _; c I^ on which features of a variation of the function % are showed.

Select set I on the basis of the analysis the change structure Sey . I^ correspond fragments FR^ c S^ . Ob tain set of intervals Ijy (j = 1, s) on the basis of the analysis fragments FR^ c Se. I j is the base for the analysis of features ;(y) . Intervals I j can contain subsets which do not reflect the feature of the nonlinear function ;(y). Under the function features we to understand the loss of continuity, the appearance of flexes points, function extremes on an interval I j . All these features are indications of nonlinearity examined function. Name the set I j having such features, informative [25, 29].

Statement 2 [25]. Let on some interval Ij functions i x    de(t) 1   (        x

Me (t) =—— M Mk (t) = dy J < s dks (t) 1 dy J

V j = 1, s   (7)

are not continuous or in their behaviour there are features. Then the interval I ^j is the informative.

Property of informative value depends from h -identifiability of structure S .

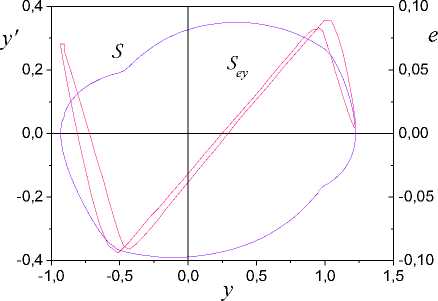
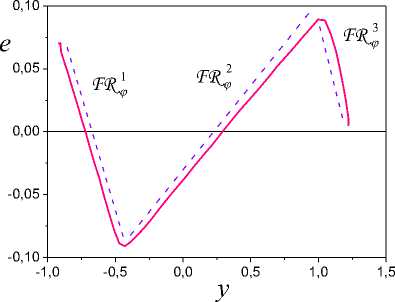
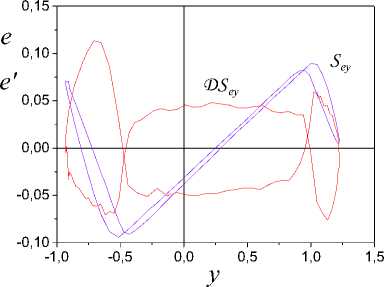
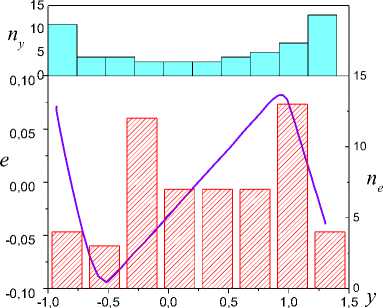
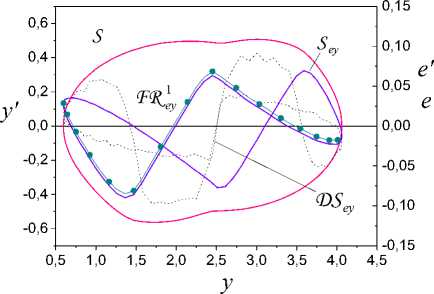
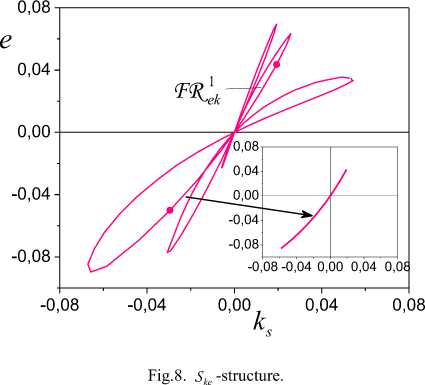
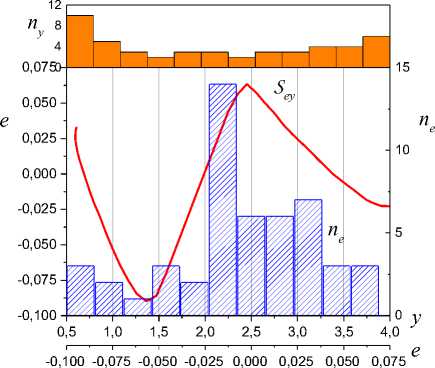
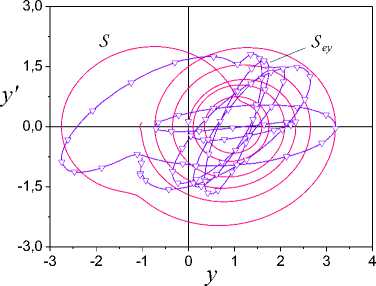
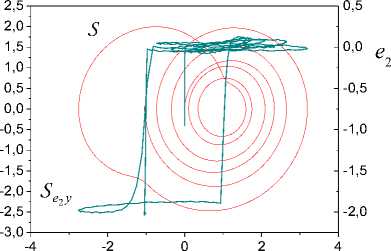
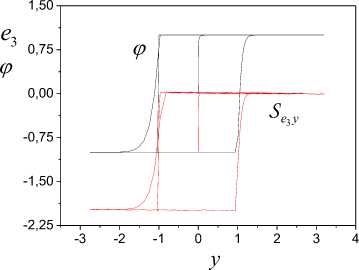
On the basis of the analysis the change parameters (7) eliminate spurious subsets Ij . The remained sets Ij include in I v i,=ui;(iy),    v

i

So, the informational set I c I^ is obtained. Consider the problem of estimation the class nonlinearity ,(y) on the basis of the analysis I . Apply results of work [30] for construction of sector set for FR^ c S^ in space Pye =⁽y, e).

Consider a fragment specified on Ii for 3i > 1. Apply LSM and determine the secant y, for FR, on I,.

Y = у (y (t)) = ay (t)+bi.      ⁽⁸⁾

Compute on Ii c I^ mean y for y(t). Let y is a centre FR¹_ф on Ii_y c I^. Draw on the plane (y, e) the straight line Y = y parallel an axis of ordinates. Obtain on the intersection of this straight line and the secant Y the point a = (y, e(y )). Through the point a draw straight lines

• ^Y, - = a,-y⁽t)+b,

• Yi, + = a,+y^(t)⁺bi,

where a_{i +(}= a_i ± c, c > 0 is a specified value.

Obtain set

Seca,( FRY ) = ( Yi,-, Y,+ ), which we name sector set for FR i . Present sector Sec (FRY) as

Sec (FRY ) = Sec„,i (FRY )^ Sec«,r (FR. ), where Secal (FRY), Seca,r (FRY) are subsets Sec (FRY) which are disposed at the left and on the right point а .

Construct secants

Yi = a.,iy⁽t)⁺b,i, l,r = a,гУ⁽t)⁺bi,r          (9)

for each of parts FR     of the fragment FR . Here

• a, b are some numbers. Next, apply the following modification of statement from [30].

Let exists such ^ > 0 that

I ai, l ^-ai\^ ^Si-   all,r ^-ai\^ ^l.           ⁽¹⁰⁾

Theorem 2. Let for system (1) in space P = (y, e) :

• i)    structures FR ⁱ FR ⁱ , described by mappings

Гey,l(r) : {У}1,l(r) ^{e}i,l(r), {У}i,l(r) ' IY , Mi,l(r) ' IY , and corresponding to them secants (9) are obtained;

• ii)    for FR ⁱ the secant (8) is obtained.

Then: 1) function y(У) £ F_ov if it is fulfilled (10); 2) function y(У) £ F_mv if it is not fulfilled (10).

The proof of the theorem 2 is like the proof of statement [30].

From the theorem 2 follows, if conditions (10) are fulfilled, then for y(У) fair the Helder-Lipschitz condition. Therefore to sectors Sec_a;(FR^), Sec_{a r} (FR^,) operation of a homothety [31] is applicable.

Another approach to the estimation of the class nonlinearity F_h is based on construction of sector for y(У) in space P_fe = (k_s,e). It is based on proposed in [30] method..

Let y(У) £ F c F_m„. Consider methods of identification structure (form) hysteresis y(У) on the class F_mv.

• VII. Estimation of Structure Hysteresis

The problem of structural identification nonlinear systems is complicated. The general approach of its solution is not designed. Each class of nonlinearity has the features. They in a behaviour of trajectories system are reflected. Detection of these features in the conditions of uncertainty gives the detailed analysis S . Despite the specified complexities, we will describe procedure for estimation structure of the hysteresis. It on the phenomenological analysis S is based.

Procedure SP for the estimation of structure hysteresis Y⁽У).

• 1.    Determine model (5) on set I = I . \I and form g      ent tr

• 2.    Check h -identifiability of system (1) on the basis of the analysis structures S , S . If the system (1) is h -identifiable, then go to step 3, otherwise end the procedure.

• 3.    Check the condition of structural identifiability of system (1). Apply results of section 5. If the system (1) is h -identified, go to step 4, otherwise end the procedure.

• 4.    Determine the belonging y(У) to the class of multiple-valued functions. Apply to the analysis of structure S the method proposed in [30]. If Y(У) £ F_mv, go to the step 5, otherwise end the procedure.

• 5.    Perform a phenomenological analysis of the structure S_ey. It determines change features y(У) ■

the variable e(t) on I .

The obtained parameters which describe features of the hysteresis on the step 5 are the base of the decisionmaking about structure y(У).

Consider examples of systems with the hysteresis Y(У) and apply procedure SP.

• A.    System with saturation

Consider the system (1) of the second order with the following parameters

-4

x(0) = 2, x'(0) = 1,

u(t) = 2sin(0.1^t), у = x, x e R .

The system was integrated with the step 0.2s on the segment [0; 30]s. Were formed sets Io, IWg . y(У) was described as и if у > 1,

ф(у) = sat(у)  к if у < 1, и if у < -0.5, where и = 2, к = 2, и = -1.

The structures described the steady-state of work system are shown on Fig. 1.

The phenomenological analysis shows that nonlinear function has on Js linear growth. Function ф(у) is restricted for Vу £ Js . The minimum distance between two fragments S does not exceed 0.025. Therefore, identifiable function has no loop. Explain the existing distance between fragments S dynamic properties of the system.

Fig.1. Structures S , S systems of the second order with saturation.

Fig.3. Fragments S on a time gap [17.2; 27.4]s.

From Fig. 1 we see that at the left and to the right of the pointsу = -0.5, у = 1 (structure S ) function e(y) sharply changes the properties. Variable e on the interval (-0.5; 1) has linear growth. The variable e out of the specified interval has fast growth (decrease). The structure analysis S confirms this conclusion.

Fig.2. The structures confirming properties ф(у).

Introduce the framework DS described by function Г_е,: {у} ^ {e'} , for verification of the obtained inferences. The change of structure DS is shown in the Fig. 2. Function e'(у) for Vу e Js c J_y has quasi-stationary value ±0.04 . Explain quasi-stationary e'(у) on the interval Js = (-0.5; 1) effect of dynamic properties the system on DS and the uncertainty which gives model (5). Out of a range J ^s , we observe transition from one operating mode of the system in another.

Go to an estimation of parameters ф(у). Partition the upper part of the framework S defined on the time gap [17.2; 27.4]s, on fragments FR^ , i = 1,2,3 . They are showed in the Fig. 3.

Fragments FR ⁱ correspond to fragments FR ⁱ on S_Ek . Consider the fragment FR2 _k c S_ek for determination of the angle inclination function ф(у). Apply secant method [26] and for the angle of inclination ф(у) obtain 2.03. The linear part ф(у) is defined on the interval (-0.5;1). For areas of saturation ф(у), we have estimations U = 2, и = -1.

Remark 5. We use structure S and secant method for identification of structural parameters ф(у).

-0,10        -0,05         0,00         0,05         0,10 e

Fig.4. The Structural-frequency chart for ф(у).

We give the representation of the identified hysteresis in the form of structurally-frequency charts (SFC) as the confirmation of the obtained results. This class of chart is offered in [32] and on the structurally-frequency analysis of the data is based. SFC is one of the effective methods of decision making under uncertainty. The frequency analysis is the development of the method histograms applied in statistics. Difference from statistical interpretation of frequency: frequency of occurrence the determined signal certain level is reflecting of properties function. Example SFC shows on Fig. 4. Here n, n are the appearance number y, e.

Fig.5. Structurally non-identifiable system of the second order (11).

Remark 6. Structural-frequency analysis is applied for solving various problems of analysis dynamic systems. The example shows that correct interpretation of results expands decision-making possibilities in systems of structural identification. SFC is applicable also in the system of identification eigenvalues dynamic system.

• B.    System with static hysteresis

2.5

Consider system of the second order with a matrix A from section VII.A and the hysteresis

a (y - d)

Ф⁽У) ='

1.5

2.5

a y

1.5

if((У^-d)>^u)&(y'>0), if((У^-d)<^u)&(У'>0), if((У^-d)<и)&(y'>0), if (У > ^u) & (У' < 0), if (У < ^u) & (У' < 0), if (У < и) & (У' < 0),

where d = 1, и = 2.5, и = 1.5, a = 1.

Consider the example NS -structure. Let

u(t) = 3 -2sin(0.Ut), y(0) = 3.5, y'(0) = x'(0) = 2.

Apply the proposed approach and obtain phase portrait S and the structure S for the steady state of system (Fig. 5). Structures on the time gap J = [8.4; 29.2] s are obtained.

From Fig. 5 we see that structures S and S are asymmetrical comparatively the straight line y = 1.5. The asymmetry difference between the left and right parts of the structures S , S gives. Appearance of uncharacteristic features in the change of the structure S (the change e in the neighborhood of the point y = 2.15) name S_e--defectiveness of structure S . Such behaviour of system explains inadequate choice of an input u(t). Structures S , S are h -identified, but they not are h -identified. For fragments F^l,F^r of structure S secants (6) are determined and for them are obtained parameters a =-0.038, a^r = 0,041.

Let ^ = 0.02 . Apply the theorem 1 and obtain that S is NS - structure. The confirmation of the “defectiveness” of the hysteresis gives Fig. 6. Curves 1 and 2 in the Fig. 6 are "the defective" and reference hysteresis Ф⁽У ).

Fig.6. Defectiveness ф(y).

Fig.7. Structural identifiability of system the second order with (11)

Let u(t) = 5 - 5sin(0.1^t). Show for this case corresponding structures in Fig. 7. Defectiveness of structure S is absent. Hence, the system is h -identified.

Go to the identification of the structure ф(y). Execute the phenomenological analysis of structures. We also consider DS -structure shown on Fig. 7. DS shows the rate of change ^(y). Se-structure has 3 critical points Icr ={1.5, 2.5, 3.5}.

We accept value d = 2.5 -1.5 = 1 for the distance of hysteresis. The segment J{ = [1.5,2.5] for y‘ < 0 growth ^(y) corresponds. This follows from behavior y‘(t) and structure DS^ on J} . Function ^(y) on the interval J² = (2.5,3.5) on which y‘< 0, goes into saturation. The structure DS transitions on the lower and upper parts of the hysteresis loop describe. This conclusion is true for a case y ‘ > 0.

Determine the angle of inclination ^(y) on the interval J¹ . The range of values framework S does not give an adequate estimation of the parameter a in (11). In [25, 26] the secant method in space P is applied to the estimation the angle of inclination function ^(y) .

Consider the upper part of structure S . On Fig. 7 it is the curve with a marker. Select on this curve the fragment FR¹ defined onJ¹ . Approximate FR¹ the secant

Yc = cy + d .                   ⁽¹²⁾

S corresponds the structure S described by function Г_ек : {k_s (t)}^{e(t)} . Here k_s (t) is the coefficient of structural properties. Select on S the fragment FR¹ (Fig. 8). It is transformation FR¹ . FR¹ is defined on the interval J¹ and to it there corresponds the secant

Ya = a^ks^{+ b} .                  ⁽¹³⁾

parameters function ^(y) in space P_ke.

Definition 2. The estimate of parameter a is a_y -acceptable if it is the result of the analysis the fragment structure S .

Definition 3. The estimate of parameter a is a -adequate if it is obtained on the basis of application the secant (13).

Statement 3. If the estimation a in (13) is a -acceptable estimation of parameter a in (11), then the secant (13) gives a -adequate estimation of the change of a corresponding fragment of the function ^(y).

Proof. Structures S , S describe the change of variable e . Hence, secants (12) and (13) should give the equal forecast of a change e(t).

Therefore we have aks + b = cy + d .(14)

Obtain from (14) for a expression a = —(cy + d - b) = -(cy + d - b) y .(15)

ks

As a is a -acceptable estimation, then we can believe a = y, where y e J{ is some number. From (15) obtain e = “(cy + d - b) y .

Therefore

From (13) follows that the factor a has dimension y . The range of values function (11) is defined changing of the variable y . Therefore, we realize identification of e = 4( cy + d - b) y ~ cy + d, where c, d are some numbers.

So, use a -acceptable estimation a in (13) is adequate to the construction of a secant (12) in space P .

So, we have shown that obtaining a -adequate estimations ^(y) is based on hysteresis identification in space Pke =(^k,^e).

On Fig. 8 show S -structure for the system and the fragment FR¹ between two markers.

We define for the fragment FR1 secant (13) with parameter a e[1;1.22] . Calculate on the ends of the segment J1 of value function ^(y) . Estimations are obtained for и and и : и = 1.5 , U = 2.5 . We have deter mined secants SEk for y 6 J1 and have obtained confirmation of these estimations. Calculate parameters of the loop for the case y' > 0 on the base d. Define diameter of the hysteresis as diam ^( y) =  sup | ^( y) - ^( yj )|, j * i,

(y,yj )eIN,g where y = y (t i), ti e Jg .

The hysteresis has extremes in the saturation region. Therefore diam<^( y) = ф(й ) - ф(и) = 1.

Fig.9. SFC for function (11).

Present in the Fig. 9 SFC for the case y'< 0 . Frequent function n_e confirms nonlinearity of function ^(y). The laws of change n and n have correspondence on the level of values frequencies.

• C.    System w th Dynam c Hysteres s

In the sections VII.A, VII.B we first presented the equation of the original system. Next we have applied the offered method and algorithms. In this section realize the offered approach and suppose that the system equation is not known. In the end of section the equation of examined system present for confirmation of the obtained results.

So, let for system (1) is the set I (4). Construct the model (5) and form the variable e(t) for t e[0;7]s. The model has the form x (t) = [-0.12;14.68;0.1]T [1 u(t) y(t)]T.

Coefficient of determination r_x²= 0.97 . Show the structures S , S in Fig. 10. We cannot make the solution about the class of function ф(y) by the form structure S . Consider two hypotheses.

• 1.    Model (5) is inadequate to system.

• 2.    Model (5) is not applicable for the given class of systems.

We reject the first hypothesis, as the coefficient of determination is very high. Therefore, the second hypothesis is true. Hence, the model has more complicated structure. Suppose that nonlinearity is described by a differential equation (compare S and S ). Examine this hypothesis.

Fig.10. Structures S , S_ey .

Determine second derivative y(t) by means of numerical differentiation. Designate the obtained variable as x . Consider model

5c^ (t) = H [1 u (t) y(t)]^T .

Let the variable x is more informative, than x . Apply LSM and obtain

5cl, (t) = [0.961;1.91; -0.982]^T [1 u(t) y(t) ]^T,      (16)

r₂² = 0.987 .

Model (16) is obtained for t e[0;7.8]s. Introduce the variable e₂ (t) = 55l (t) - x₂ (t) .

y'

y

Fig.11. Structures S , S_ey .

Show on the Fig. 11 frameworks reflecting the state of the identification system. We have presented in Fig.11 the framework S described by mapping

Ге2y :{y} ^ teh

The Fig. 11 allows to make the solution on the hysteresis form in system. This confirms the structure S . S e2 y      e2 y is the modification of the ideal hysteresis. We see that the variable e in the saturation region contains small fluctuations. Analyze the nature of these fluctuations.

Assumption. The fluctuations are property of the system or the effect of the uncertainty caused by the inadequacy of the model (16).

Apply to check of the assumption model x2(3)(t) = HT [1 u(t) y(t) x/t)]T .            (17)

Obtain the estimation of vector H on the time gap [0;7.8]s: H = [0.99; 1,06; -1; 0,06]T , r₂²= 0.996.

Let e₃(t) = x2₍₃/t)-x₂(t). Show in Fig. 12 the framework S_e^_y describing the change of the hysteresis ф(y).

Fig.12. The original hysteresis ф(y) and its evaluation e₃ (y).

Compare S , S and obtain that framework fluctua-e2 y e3 y tions S are effect of inadequacy of model (16) in the saturation area. Show in Fig. 12 the change of original hysteresis ф(y) . S^y coincides with ф(y) . Displacement is result of transition in structural space.

Remark 7. We do not consider the problem of choice the time gap for identification of models (5), (16), (17). Its choice depends on the properties of the system and is determined on a simulation stage.

So, the offered approach to structural identification is efficient at the estimation of various types a hysteresis. Begin at the initial stage of identification with the analysis of structure S . If the analysis does not give information about the hysteresis form, then realize the procedure described in this section.

Now determine parameters of structure S and obtain the equations describing the original system. Apply the approach stated in section 7.B. Estimate the diameter and the distance of hysteresis. The hysteresis is described by the dynamic law. Therefore, determine a form of input variables which form the hysteresis.

Apply numerical differentiation and find the first derivative e(t). Designate the obtained derivative as v(t). Consider structure S for identification of dependence between v(t) and y(t). Describe S function

^Гvk : {kv,y (t)}^{v(t)}, kv,y (t) = v(-) .

Determine the secant S . Simulation results show inadequacy of structure S . Hence, nonlinear dependence is between v and y . Therefore, consider structure S with

Гs. : {ЧXt)U{v(t)}, 4 (t) = -^(t)

^{vksy        sy                          sy}        sgn(y(t))

where sgn(-) is the sign function.

Results of simulation show that the structure S is linear for almost all k . Therefore, we suppose that the dynamic law of the change ф(y) depends from sgn(y(t)) . This inference is fair and for function ф(sgn(e3 (t))). So, we have the following law of formation the hysteresis v = -аеъ + ^sgn(y) + уsgn(e3).          (18)

Fulfils verification of the proposed structure of the hysteresis at the stage of parametric identification. Here this problem is not considered.

We examined RC-OTA chaotic oscillator [33] described by the system of equations

x - 0.1 x + x = ф

Ф = 10 (-ф + sgn (x + sgn(ф) )),

x (0) = 0, x (0) = 0,ф(0) = 0.

The system (19) was integrated with a step т = 0.08s. The spectrum of eigenvalues of system is (0.05 + .99i;0.05 - .99i;-10). The system (19) is unstable. But the proposed approach identifies the structure of the hysteresis. Notice that the law (18) also is applicable for description RC-OTA of an oscillator.

• VIII. Conclusion

The method of structural identification of dynamic systems with a hysteresis is developed. It is based on selection of the set containing the information on properties of the nonlinear part system. On the basis of this set is obtained the virtual structure S which gives the solution of problem estimation to hysteresis structure. The concept of structural identifiability system at level S -structures is introduced. The demand of structural identifiability is the necessary condition of estimation the form of hysteresis. Criteria allowing to estimate the structural identifiability of system, are proposed. The problem the selection of the class hysteresis functions is solved.

Procedure of structural identification hysteresis is designed. Procedure implementation on the phenomenological analysis of structure S is based. We the phenomenological analysis understand as selection in S features and the properties, allowing to identify the hysteresis. Nonlinearity has the features. Therefore, their identification gives only the specific phenomenological analysis of structure S еу . We show effectiveness of such approach. Algorithms of estimation structural parameters of the hysteresis are described. They are based on the transition in special structural space and the application of secant method virtual structures. We show that this approach adequate to estimate the parameters of the hysteresis is gives. The method of the structurally-frequency analysis for check of the obtained results and estimations is offered. It gives the representation of fragments structure S еу in two planes and ensures conducting comparative the analysis of correspondence of parameters fragments. We show that the proposed methodology to unstable dynamical systems is applicable.

In conclusion, we will note that the proposed approach to structural identification demands certain qualification from the researcher.