Structural Identification of Nonlinear Static System on Basis of Analysis Sector Sets

Published Online December 2013 in MECS

Various approaches and methods are applied to identification of nonlinear static systems. In [1-3] the statistical methods based on the correlation and dispersive analysis are used. Application of adaptive methods of identification is considered in [4]. Wide application have genetic and network algorithms [5, 6] and their combinations with various methods of approximation [7, 8]. In [9, 10] the aprioristic information and the subsequent approximation on the set class of functions [2, 11, 12] is used. The choice of a class of nonlinear functions is not always given.

Difficulties of structural identification of static objects explain following factors [13]:

• i)    the system output is the integrated magnitude reflecting influence of set of input variables;

• ii)    absence of the methods, allowing to allocate necessary interrelations "input-output" for the purpose of classification of a form of nonlinearity. Approaches to an estimation of degree of nonlinearity of system are stated in [1, 3]. The solution of a problem of an estimation of degree of nonlinearity is a key to a choice of a class of nonlinear static models. It is based on application of a complex mathematical ap-

• paratus and do not allow to offer approaches to structural identification;

• iii)    attempt of the a priori representation of nonlinear structure [2, 14] on set of existing inputs within the limits of the parametrical approach demands a solution of a problem of a multicollinearity [14-16]. The problem is complicated, and it’s solution simple. It is explained by conditions of practical realization of models. This simple decision (exception of dependent variables) is applied widely in real control systems. But such approach does not allow to solve a problem of structural identification. Unfortunately, such interrelation not always is understood and in existing methods practically is not considered;

• iv)    application of parametrical methods on the specify class of polynomials [2, 17]. Efficiency of such approach depends on experience and intuition of the researcher. It demands performance of preliminary labour-consuming researches. Such approach does not allow to define nonlinearity structure in an explicit form. Wide application of parametrical methods in problems of structural identification explain their simplicity which in considered specific area not always givens effective results.

For the decision of the specified problems in [18] the methodology of structural identification of nonlinear static systems with a vector input in the conditions of uncertainty is offered. Systems can contain singlevalued and multiple-value nonlinearities. In [19] the method of structural identification of nonlinear static systems on a class of single-valued nonlinearities with a vector input in the conditions of uncertainty is offered. On its basis the algorithm of decision-making on nonlinearity structure is developed. The decision is searched in special structural space [18]. The approach to structural identification of nonlinear systems with a vector input [18] has allowed to make the decision in the conditions of a multicollinearity [14]. Despite essential advancement in the given direction of researches there is a set of problems of structural identification of nonlinear systems.

One of such problems is decision-making in systems of structural identification about a class of nonlinear functions. The given problem in the conditions of uncertainty was not studied.

In work the decision of the given problem for static systems with a nonlinear input and several nonlinearities is given. For this purpose we work in special structural space (SS), which reflects properties of a nonlinear part of system. Into the SS work in structures S v (vir tual portraits) [20]. We analyze properties Sv on set of linear functions (secants). Offer a method of construction of sector sets, to which belongs Sv . Analyzing sector sets, we make the decision of a class of nonlinear functions (single-valued or multiple-valued). Unlike [18, 20] for construction of sector we use a Holder condition. Further we describe the criteria of decisionmaking, based on the theory of proximity of sets, and procedures of an estimation of structural parameters of nonlinear functions.

• II.    Problem Statement

Consider the system, described by the equation

У п = AU n, + B T f (U , n ) + - . ,               (1)

where U_n e R^k , y_n e R are an input and an object output; и _n e U_n is the limited irregular function depending from n and possessing property limiting nondegenerate; n e J_N = [0, N ] is discrete time; A e Q₍ c R^k is the vector of the parameters, belonging limited, but a priori to unknown area Q_A ; B e R m ; ^ e R is a perturbation, | ^ | < w ;

f ( U , n ) = [ f ( U^ n ), f 2 ( u _{p 2}, n ), ^fm ⁽ u p m , n ) ] ^T ,

f ( ^up и) is a limited function, p. e [1, m ] , m <  k .

For (1), (2) the information set is known

I o = I o ( y , U ) = { y , , U n , n e J n = [0, N ] }    (3)

and mapping corresponding to it

Г.:{Un}^{yn}. VneJN describing an observable information portrait [18].

It is necessary on the basis of the analysis (3) and F_o to estimate structure of vector function f ( U , n ) .

• III.    Set for Estimation f ( U , n )

For data acquisition for the decision of a problem of structural identification f(U,n) we will use the approach offered in [18,  20]. Consider a variable sn = ITUn, where I e Rk is an unit vector, and apply model y5 n = assn . Define parameter as e R from a condition arg min (ys,n — у, )2 =

From made above assumptions estimation existence follows a ˆ .

The variable e^ = г и — y^ contains the data about n       s,n       n nonlinear function f(U,n) . Generate set

• ¹    e = { e n , ^U n , n ^{E N} } ,                       ⁽⁴⁾

Such method of construction I excludes domination of any input object.

Mapping F_e : { u_z.} ^ { e „} does not allow to solve a problem of structural identification of system [18]. Explain it to that e_n e R has irregular character and does not satisfy to Holder condition. We will write down this condition [21].

Let on a segment [ a , b ] continuous function z ( х ) , belonging to limited set Q , is specify. Then function z ( х ) satisfies to Holder condition of an order i 9 , if is such constant X , that for any the ( x_x , x ₂ ) e [ a , b ] inequality is carried out

| z ( x_x ) — z ( x ₂ )| <  X X i — X 2 Г , 0 <  ^ <  1.      (5)

As norm in (5) we use a maximum of the module of a difference of coordinates.

At Г = 1 from (5) receive Lipschitz condition. For irregular functions Г «0 . Sometimes (5) name the Holder-Lipschitz condition.

We explain irregular character of a variable e_n e R in the method of its reception. It does not allow to apply any regular procedures to the analysis e . Therefore to the decision of a problem of structural identification apply results of processing of set I . Further we will offer algorithms of structural identification and decision-making on the basis of the set analysis I^ (I_e) .

Here we do not consider methods of an estimation of degree of nonlinearity of object (1), (2) and a choice of arguments of a vector function f (U, n) . They are described in [19]. Therefore further we believe, that the object is nonlinear. Let the subset Un c Un, on which the vector function f (U,n) is defined, is known. Further we will consider function components f (ut) e f (U) , having ordered in appropriate way vector elements U . We believe, that the index i not necessarily should coincide with number of an element of a vector U .

• IV.    Decision-making on Class f ( u )

Consider the structural space P = ( k_{e u} , e ) , specify on set

Ik ={ke,щ,n , en , i = 1, m, n G JN } , where k „ g R there is a coefficient of structural e,ui ,n properties on a u system input

e ke,u,,n = ki,n = -----,                                   (6)

i i,n en e R is a variable, reflecting a state of processes in nonlinear system of identification.

On J arrange k     on increase. Generate set

N                      e , u_i , n

{ ^k v _q } , where A _q = k s ( e ^v , u " , q ) , q e J N = [0, N ] . The symbol v designates ordering of values k . To everyone k ^v there corresponds value e ^v , therefore we will receive

• ¹ V = { e’ v , k Vq , i = 1 m q e J N } .

Consider on I k mappings Г v , k : { k v _q [ ^ { e ^ } , i = 1, m and structures corresponding to them S k , _e . S ^v reflects change of processes in nonlinear system of identification object. Properties S ^v are researched in [18, 20]. The virtual structure S ^v has universal character for single-valued and multiple-valued nonlinearities.

For development of criteria of decision-making on a class of nonlinearities execute clustering sets Iv . De- fine the first difference Au,. „ = u. „.! — u. „ and I di, n         i, n 1          , ne vide into two subsets

I e = I e, +     I e, — , where

(en,u,n) e Ie, + = {en e R,ui,n e R | Au,,n>

(e„,u,n) e Ie, — = {en e R,u,,n e R | Au,.,n<

#I e , + + #I e , — = #I e ,

# designates a cardinal number of set.

Generate the sets IV + (Ie + ), IV (Ie ) ordered on kv , kv . Consider the structure Sv  set by map- ping Гvek . In [19] it is shown, that for multiple-valued nonlinearities of the analysis Sv it can appear insuffi- ciently for a structure estimation f(u  ). Therefore in

• [18] at the decision of a problem of structural identifica-

• tion of a hysteresis mapping

г ; .,: { k V, .— } ^ {     .

and structure corresponding to it was applied SK ^v Further we develop and generalize the given approach.

Consider sets I V ₊ ( I_{e +} ) , I V ( I_e ) and structures (virtual portraits) S ^v , S ^v corresponding to them, described by mappings

Г V , k , , + : { ^k'q , . } ^ { e ; ,} ,                          ₍₇₎

^г V , . . . :{ k q, , [    ’ e V .} . ’

For each structure S ^v , S ^v find a secant

• Y . , q, + = Y ( e q , + , k- q , + ) = a - + k .V „,

,             .                 I = 1, m ,    (8)

Yi. q,— = Y (eq., k-q.)=aV—kq.,—, where av , av define by means of a least-squares method. We will designate coefficients of determination for secants Y , Y as r2., r2 .

, + , — , + , —

Factors av , av are estimations of average values u , u an input u , belonging to sets I , I . Owing to an irregularity u these estimations can not coincide. We will designate the average value u re ceived on the basis of processing I , as u . Let exists such 5V > 0 , that

| a ^V ± - U , J ^ 5 , ,

Statement. Let for  object (1),  (2) in space

P = ( k„,, , e ) structures Sv , „ , S v  „ , described by

• e , U i                                      k ^ , + , e         k , , e

mappings (7), and secants corresponding to them (8) are received. Then:

• i)    function f ( u  ) belongs to a class of single

valued nonlinearities F , if (9) is trule;

• ii)    function f ( u  ) belongs to a class of multiple

valued nonlinearities F , if (9) is false.

Proof. At partition I into two subsets I ,I we have two estimations u , u (their values give a ^v , a ^v ) average value of a variable u . As the variable u is irregular function, values u , u is possible to consider as admissible estimations u . u , u are received on the basis of the analysis of structures S ^v , S ^v . Performance of a condition (9) says that, a variable e , and, hence, and f ( u ) satisfy to a condition of Lipschitz (5) with a constant X on set of secants.

If the inequality (9) is false, nonlinearity f ( u ) has the complex form. Hence, on set I ^v function f ( u ) can be presented two structures S ^v , S ^v , which there correspond parameters a ^v , a ^v . As the condition (9) is false, function f ( u i , n ) e F _mv . ■

From the statement we receive, that in space P = ( k_e „. , e ) for irregular function e we can construct the Holder condition.

Consider mapping Г V ₊ : { k v_ } ^ { k v ₊ } and structure SK ^v corresponding to it.

Let J, v  is a change interval kv , and J „ g J „ kq,-                                                  q,                   kq,-          kq,- is some subinterval J v . kq,-

Definition 1 [18, 20]. The structure SK v contains a islet IS of level n , if for Vkv  e J  g J'    k,  is n                                          qkq,—         kq,—      q,+ quasistationary.

Depending on properties of studied system we the structure SK ^v , described by mapping

Г;.,: {<:...:>■: k can be analyzed also.

Theorem 1. Let: 1) structures S ^v , S ^v , described by mappings (7), and secants corresponding to them (8) are set; 2) the condition (9) is not satisfied. Then f ( u ) belongs to a class hysteresis functions, if the structure SK V ₊ contains islets IS^ , j >  1 .

The proof of the theorem 1 follows from the theorem 3.15 [18] and statements.

As shown in [18], if f ( u ) is an element of structure of system (1), (2), secants (8) adequately describe change S ^v . Further we suppose, that this condition is carried out.

Definition 2. Let in space the P = ( k_{e H} , e ) structures Sv с e , ( с = + , — ) , described by mapping (7), are set and secants y_{t c} (8) are defined. Then we will say that function e v ( k / _c) satisfies to Holder-Lipschitz condition with a constant X = а'_с and 9 = 1 .

On the basis of definition 2 construct sector for S kV , c , e . Designate it ^as Sec_z ( S v, , _c , e ) ^:

Sec. (Sy, c, e ) = ( Yi, c,-, Yi, c,+ ), where Yi,c,- =( aVc - £c ) kVc , Yi,c,+ =( aVc + £c ) ki,c , ^, > 0 are some numbers.

Remark 1. In [20] the approach to construction of sector on the basis of the analysis of set of secants for a finding of borders of sector has been offered. The approach offered here is more simple. We believe that the secant adequately describes change S ^v . In this case secant parameters use for formation of sector on the basis of a condition of Holder-Lipschitz.

Further we will use concept of proximity between sets. Proximity estimation between sets receives on the basis of application of several approaches [22]. They are based as on topological, and metric proximity. Various metric approaches to a proximity estimation are described in [23]. They are based on a distance estimation between points of sets. For a considered problem the metric approach is ineffective. Explain it to that sets

Sec , ( S L -, , ) , SecJ S V .+. , )

are crossed in the be-

ginning of coordinates Euclidean plane. Therefore make following definition of proximity of sets Sec, ( SV. _ _e)

^{and Sec} , ( ^S V ,+. e ) .

Definition 3. Consider in space P = ( k_{e u} , e ) structures

’V _ e c Sec, (sV _ J. Sk' + e c Sec, (sv' + J k.,  . e               , —  \    k.,  , e /       k.. +. e               , +  \    k., + , , / and secants Ytq -. Ytq +. described by the equations (8). Then structures SV.—.e. SV.+,e we will name approximate and we will write SV _,e 5 SV + . if d (SV,—,e. SV,+,e ) = min |<+— ai, — I .

Definition 4. We will say, that sets S ^v , S ^v are

5 -approximates and we will write SV __>e 5 SV _{+ e} , if

d. (SV..—,. Sk... e ) = aV.— a^s =5 . =. a 0 (10)

Consider the structure Sv , described by mapping ГV k : {kviq } ^{, }. and a secant corresponding to it Yt.q = a. Ц,q, where aV there is an average estimation U n. Apply to sector Sec, (SV + e) transformation of homothetic [24] with the factor equal to unit, and turn of the beginning concerning of coordinates on a corner of 180 degrees. The received set designate as H (SecJ S,,)). Let quarters of a plane E . Let aV+ < a^_ that is the angle of slope of a secant y q _ is more than at y q + . Apply to set Secx (SV, + e) operation of homothetic and receive set H(Secx (Sk + e)) . Let the condition (9) is satis fied. We find intersection of sets Secx (SV _ e) and

h (Sec». ( s;.+,)).

R Se.- (SV,_,)ПH(Sec,, (SV+,)).

Considering theorem conditions receive R ^ 0 . Consider the structure S ^v , described by mapping ^{Г V} . k, ^: { ^ki,q } ^ { e V } . Define ^for a ^SV.,e secant Yt_q = a^Vik^v_iq . where aY is an estimation of average value on an interval J ^v . From a condition (9) we receive Y_t . q e R . Then

I a',,— aV—|= |aV+— aV— ± a-     25,-

Designating 2 . = = . receive (10). So. sets Sec , ( ^S V ,—, e ) and H ( ^Sec , ₊ ( ^S k , + , e ) ) are . = -appro-ximates. ^

Theorems 2 gives conditions of decision-making on a function class f ( u ) .

i i , n

Corollary 1 from theorem 2. If SV. _ _e . SV. + _e. then f. ^{( U}t, n ) ^e FmV .

Corollary 2 from theorem 2. If SV. _ _e 5₀ SV. _{+ e}. then sets Sec , ( S kV. , _— , _e ) and H ( Sec , ( SkV. , ₊ . _e ) ) are approximate with the metrics

R=Seci_( SV,—, )n H (Sec, ( SV . ,)).

d ( e_ . e . ) = inf | e . — e^V |.

Theorem 2. If the condition (9) is satisfied and the secant Y _q = a^k^ structure S V. _e belongs to set R . then structures SV _., SV _{+ e} are . - approximates.

So, we have offered methods of decision-making on a class of identified nonlinearities. The received results allow defining a quantitative estimation of nonlinearity of system (1), (2) on set an input. Also it is possible to enter relative indicators

Proof. Consider a Euclidean plane E . As shown in [18]. structures S ^v , S ^v locate in the first and third

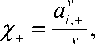
a t —

X — = -v . a^v

which values compare with 1. If X- — X | — ^ , where e >  0 is some specified value then f. ⁽ U n n ) ^e F mv .

Application of the approach, based on the analysis S v to an estimation of structure f(u ), has shown that for each function f(u ) the specific approach should be used. Therefore further we will consider a case, when f (U, n) e R2 contains a power function f (и „ ) e Fov and saturation function fJ (Uj, n ) = fs (Uj, n ) e Fsat C Fmv max r^v  ^ P *,                       (14)

j     e Y1, p where r2 is a coefficient of determination between e У1, p ev and kv .

Let

5 * = r k ( p * ) ,

Describe the approach to structural identification f ( u)) e F_v with the definition of boundary for change of coefficient of determination. Consider mapping

^Г Vk 1 ( K ) : { k 1 Vq ( к )    < e q } .              (16)

^{f ( U} i ) = u ,

^fs ^{( U}j , n HaU ^Uj , n ) = <

в, uj,n, a,

« <  ^Uj,n <  ^в , u, „ <  a ,

where k v_q ( к ) is a coefficient of structural properties system identification with an input u K .

Г V k , ( к ) corresponds structure S v _е( к ) in space P = ( k v , e v ) • We will construct for a S^ _e ( к ) secant

where к >  0, a >  0, в >  0 are some numbers. received results generalize on the general case.

The

Let two inputs u, e U, u; e U with the maximum coefficients of determination are defined with e e R . Further we will designate these inputs as ц, i = 1,2 , where 1 is i , and 2 is j . For everyone u construct structures Sv, Sv. Let by means of the statement i , , e               i , +, e and the theorem 2 f(u) are carried to classes F or ii                     ov mv .

• 5.1    Case ^{f ( U} 1 ) ^e F

Let f (uv) e Fov is described by the equation (11). For the f (u,) e Fov structure SX with application mapping is constructed ГV and the secant, described by a polynom of degree is defined p , pj

/1, p ( e , k1, q )= Y1, p = a 0,1 +^ a 1, j ( k1, q ) • j=1

Order of a polynom (13) define as

Y (ev , kvq (к))= Ук = a 1 kvq (к)

and define a coefficient of determination r2v.

^e У к

Theorem 3. Let for system (1) with f (U, n) e R2 and f(u), described by the equation (11), in space P : i) the structure S v , described by mapping (16), and a secant у p (ev, kvq ) (13) is constructed; ii) the order of a polynom (13) satisfies to a condition (14); iii) for the S^ ?(к) secant (17) is constructed and the coefficient of determination is defined r22_ . Then f (ux ) e F , if e ук                       -,n-        ov the parameter к of function (11) choose of a condition

' v — e У к

- 5 * 1 ,

where A, — 0 is some size, 5 2 is defined from a condition (15).

The proof of the theorem 3 is based on application of the theorem 3.6 [18].

The condition (18) allows making the decision on a form f ( U j _n ) e F_ov in the conditions of uncertainty.

Corollary 1 from theorem 3. If f (ux й) e Fov and Sv ^c Sv + D then for a secant Y structure Sv (к) kl, ,e о ki,+,e                                           к                               ky,e condition is satisfied

Y e Sec , . ( S N-, )П H ( Sec , + ( S ) ) .

We modify the described approach. We will show that the adequate choice of parameter к > 0 of function f (uY n) e Fov is analogue of proximity sets Sec; (SV,-,e ) , H(Se<\ (SV,+,e )) • Corollary of it is structure straightening Sv . The term straightening is offered in [18]. It means, that the choice к adequate to that, the secant ук of structure Skе(к) has higher coefficient of determination, than a secant for Sv .

k ₁ , e

Theorem 4. Let: 1) are carried out a corollary 1 of the theorem 3; 2) the parameter к > 0 of input u choose of a condition (18). Then: i) S^ _ e (к)^ SVk^,e (к) ; ii) for a secant ук the structure Sk е(к) condition r2  > r2  is satisfied, where 5„ is a proximity of sets e Ук      e Y1                                 U with norm (10) and о - О .

The theorem 4 gives conditions, at which degree of proximity of sectors S_k _Д к ) and S_{k +}Д к ) heighten. It is true only at alignment of structure S V _е( к ) concerning a bisector of angle of the first quarter Euclidean plane.

Straightening follows from a condition r 2_ >  r 2_ .

So, we have offered criteria of decision-making on function parameters f ( u_{x n} ) e F_ov .

• 5.2    Case f ^{( u} 2 ) ^E F sat ^c F mv

Let f (u2) EFsat c Fmv is described by dependence (12). To decision-making on a belonging f(u) to a class Fsat c Fmv apply the theorem 1. Apply the theorem 2 and receive, that the secant y2,q = aVkV,q struc- ture     Skv ,e does not belong to set

R =^Sec X. ( ^S X , - , e )A H ( ^Secx₊ ( ^S V , + , e ) ) . Hence, struc^-

Consider structures S^v and S^v , described by mappings (7), and corresponding secants y₂ +, Yq-

• (8) . As estimations а, в in (12) we use [25] parameters of secants у_{г +} , y₂ _ . Let a\ _ >  a\^ . Then for а , в receive estimations

а = av+, в = a^,.(19)

For hysteresis use two parameters [26]:

(nj ,ni )e Jn j ^ l;

• 2)    distance

d (u, и , u, и ) = min | u9 и - u? и |.(20)

V 2, nj , 2, nJ    (nj, n )e jN I 2, n      2, ni I diam f(u  ) defines area of change of function.

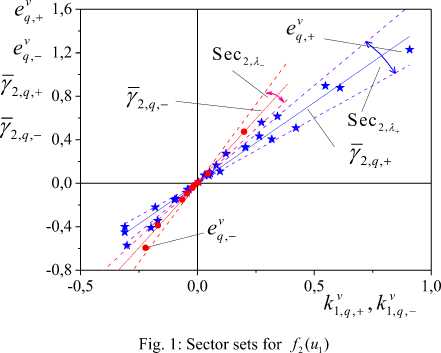
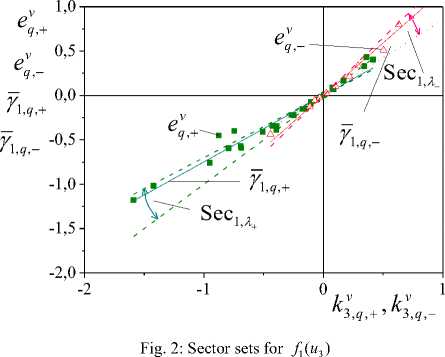
On the basis of the analysis of a distance d(u ,u ) we define a hysteresis class, to which researched function belongs. For diameter receive diam f (u2 и) = в-

As elements u_{2 n}e U_n we consider irregular, application (20) gives an incorrect estimation. Therefore we will use the set analysis I^v .

Theorem 5 [18, 25]. Let

(kV,qj,k;,qi) eql cQk c R, where k^ is monotonously changing function, j ^ l, QL is an interval of growth function f (u2 n) on a plane (kvq, evq ) . Then

d( u2,q, , u2,q. ) > П  min  । Ak2,q„ h j         '           (qj,qi )e JN            jl where AkV  = k,  - k^ ,

2,qjl        2,qj        2,ql tures Svk^,.,e and SV,+,e are not Sg - approximates.

П =

min| u _n — n | v      2,q_l

max | k2v,q  |  , k2, qj e^ k

П > 0 .

If d(u^ quu2  ) < £2 , where ^ > 0 is some set number, and Aeq > 0 for almost Vq > 0, then f2(U2,n ) G Fsat

Show how to estimate area of linear change f>(U2,n ) e Fsat . Consider mapping

Гk,.: {    .  • ^

and structure corresponding to it SK ^v . On the basis of the analysis S^v , S^v we have received estimations for а,в (19) and have generated subsets corresponding to these structures I^M_M^₊ (IM₊ ) , IM₂ _(IM _) variable change u .

Consider a plane E = (k^vv, u

) , c = +, — . Designate:

• i)    the area, limited to straight lines u₂  = а ,

u_{2 q} = 0 on a plane E, as Q_L ;

• ii)    the area limited to the graph of function

^U2,q,c = Фе (kq,c ) , as ^c •

Let L+ =QLn^+, L_ =Q,AQ •

SS allow to solve problems of structural identification of nonlinear static systems. Attempts to extend this approach on systems with the distributed lag have appeared unsuccessful. Explain it to that the distributed lag is result of the decision of difference equations. Received decisions are somewhat approximate to a variable which is a basis for reception of a lag. Therefore SS in structural space for a base variable and its lags will differ not strongly. It does not allow developing effective algorithms of decision-making. Presence of the distributed lags on variables y , is the reason of decrease a coefficient of determination between input variables and a system output.

• VII. Example

Consider object (1),  (2) with A = [1;2;3]⁷  ,

B = [0.3;1]r, f1(u3) = u°06, f;(uj = sat(U1). а = 1.5, f = 2.5 . ^ is a random variable with a zero expectancy and a final dispersion, |^ | < 0.3 . Inputs u1 n e Un are normally casual variables with a final expectancy and a dispersion. The analysis of a regularity of a variable en gives 9 = 0.11. Therefore according to (5) e is an irregular function and for its analysis execute transition in structural space P . Applying the theorem 1 [19], we receive nonlinearity of system on variables u , u . For decision-making on a class of functions f , f apply results of section 4. Define Lipschitz constants for structures Sv and Sv . Construct sector sets for structures Sv and Sv and show them k1 , e               k2 , e in Figure 1, 2.

Theorem 6. Let: a) the structure SK ^v is described by mapping Г^v_k^ : {kv_}•{kv₊ } and contains islets IS_n , j > 1; b) on the basis of the analysis structures Sk,_{+ e} and Sk, __e estimations (19) for a,f of function f (u_{2 n} ) e F_sat are defined. Then areas of linear change ^f,^(u2,_n ) ^eFsat are specify on those u_{2 q +} e L₊, u_{3 л}e L , on which there are islets IS_n .

• 2,    q^{,— — n}j

The proof of the theorem 6 is based on the analysis of change of a coefficient of structural properties k^v .

• VI. Sector Sets in Systems with the Distributed Lag

On the basis of the analysis of sector sets (SS) [18, 20] we can make the decision on a nonlinearity class. Despite complexities their construction for irregular inputs

In figures we will designate Sec₂₂ =Sec₂(S^M^^_e), ^Sec2,A_ =^Sec2_—(^Sk₂,—,e ) .

Receive estimations for parameters of secants Y : a^+ = 1.18 , a^_ = 0.75 , a^ = 0.88 , and for parameters  of secants y :   a^+ = 1.49 , й2- = 2.37 , av = 1.73 . From a basis of figures, estimations for parameters of secants and the theorem 2 we make the decision: /1 (u3) e FoV and f,(uj e Fmv . Sectors in a Fig. 1 are not approximate. To an estimation of parameter К of function f (u3) apply the theorem 2. Construct a secant (13) and receive p = 2, r2_  = 0.983. Further e Y1, p we define a secant (17) and find an estimation К = 0.52, r2_ = 0.982 . Application of the theorem 6

e Yk allows to allocate intervals of linear growth f(u).

From the Figure 1 for f(u) receive estimations of structural parameters /? = 2.38, a = 1.48 . To distance definition apply theorems 5. We receive value d = 0.1, that allows us f(u) to consider as saturation.

So, results of modelling have confirmed efficiency of the offered methods and algorithms.

• VIII. Conclusion

We are offered methods of structural identification of static systems with a vector input and several nonlinearities in the conditions of uncertainty. The problem decision is searched in special structural space. Virtual portraits of a state of a nonlinear part of system are work in. For the analysis of virtual portraits we have offered sector sets (SS). Criteria of a belonging of nonlinearity are offered a class of single-valued or multiple-valued nonlinearities. They are based on the proximity analysis SS. The received results are applied to structural identification of system by saturation and a power function. Results of modelling confirm efficiency of the offered approach.

• [1]    N.S. Raybman, and V.M. Chadeev. Construction of models of production processes. Energiya, Moscow, 1975.

• [2]    D. Graupe Identification of systems. Robert E. Krieger Publishing Co., Huntington, New York, 1999.

• [3]    L. Ljung. System identification – theory for theuser (2nd ed.). Prentice-Hall, Upper Saddle River, New York, 1999.

• [4]    N.N. Karabutov. Adaptive identification of systems: Information synthesis. Librokom, Moscow, 2006.

• [5]    M. Norgaard, O. Ravn, N.K. Poulsen, and L.K. Hansen. Neural networks for modelling and control of dynamic systems: a practitioner's handbook. Springer-Verlag, London, 2001.

• [6]    J. Madár, J. Abonyi, and F. Szeifert. Genetic programming for the identification of nonlinear input-output models. Ind. Eng. Chem. Res., v44, 2005, pp.3178–3186.

• [7]    E. Righeto, L.H.M. Grassi, and J.A. Pereira. Nonlinear plant identification by wavelets. In ABCM Symposium Series in Mechatronics, v1, 2004,

pp.392-398.

• [8]    T. Sato, and M. Sato. Structural identification using neural network and Kalman filter algorithms. Structural Eng./ Earthquake Eng., JSCE, v14, 1997, pp.23s -32s.

• [9]    S.F. Masri, J.P. Caffrey, T.K. Caughey, A.W. Smyth, and A.G. Chassiako. Direct Identification of the State Equation in Complex Nonlinear Systems. In ICTAM04-Complex Nonlinear Systems, 2003, pp.1-2.

• [10]    L.A. Aguirre, M.F.S. Barroso, R.R. Saldanha, and A.M. Mendes. Imposing steady-state performance on identified nonlinear polynomial models by means of constrained parameter estimation. IЕЕE Proc. Conlrol Theory Appl., v151, 2004, pp.174179.

• [11]    M. Espinoza, J.A.K. Suykens, and B. De Moor, Kernel based partially linear models and nonlinear identification. IEEE Transactions on Automatic Control, 50, 2005, pp.1602-1606.

• [12]    S.A. Billings, and Hua-Liang Wei. A new class of wavelet networks for nonlinear system identification. IEEE Transactions on neural networks, v16, 2005, pp.З62-874.

• [13]    N.N. Karabutov. About structures of state systems identification of static object with hysteresis. Int. J. Sensing, Computing and Control, v2, n2, 2012, pp.59-69.

• [14]    F. Mosteller, and J.W. Tukey. Data analysis and regression: A Second course in statistics. Reading, MA: Addison-Wesley, 1977.

• [15]    J. Johnston. Econometric methods (2nd ed.). McGraw-Hill Book Company, New York, 1972.

• [16]    N.R. Draper, and H. Smith. Applied Regression Analysis (3rd ed.) By John Wiley & Sons, Inc., 1998.

• [17]    A.G. Ivachnenko, and J.A. Muller. Selbstorganisa-tion von vorhersagemodellen. Veb Verlag Technik, Berlin, 1984.

• [18]    N.N. Karabutov. Structural identification of static objects: Fields, structures, methods. Librokom, Moscow, 2011.

• [19]    N.N. Karabutov. Decision-making on structure of univalent nonlinearities in system of structural identification of static systems. Int. J. Sensing, Computing and Control, v2, 2011, pp.103-110.

• [20]    N.N. Karabutov. Structures, fields and methods of identification of nonlinear static systems in the conditions of uncertainty. Intelligent control and automation, v1, n2, 2010, pp.59-67.

• [21]    E.G. Shilov. Mathematical analysis. Fizmathlit, Moscow, 1961.

• [22]    V.A. Efremovich, and A.K. Tolpygo. Geometry of proximity. FIMA, Moscow, 2007.

• [23]    A.B. Petrovsky. Space of sets and multisets. Editoral, URSS, Moscow, 2003.

• [24]    G. Choquet. L'Enseignement de la geometrie. Hermann, Paris, 1964.

• [25]    N.N. Karabutov. Structural identification of static processes with hysteresis nonlinearities in civil engineering. J. of Civil Engineering and Science, v1, n4, 2012, pp.22-29.

• [26]    Krasnoselskiy, M.A. and Pokrovsky, A.V. Systems with hysteresis. Nauka, Moscow, 1983.

Nikolay Karabutov is the professor of department Problem of control of Moscow state institute radio engineering, electronics and automation. The professor chair of mathematics of Financial University under the Government of the Russian Federation. Dr.Sci.Tech. The research area is the automatic control theory, identification, adaptive control and decision-making.