Structural Identification of Systems with Distributed Lag

Published Online October 2013 in MECS

Models with the distributed lags are widely applied in an econometrics and economy [1-4], the engineering [57] and medicine [8-10]. Delay can have both independent, and dependent variables. The account of the distributed lag activates autocorrelation between variables [1, 2, 4] and complicates process of identification parameters object. To identification of parameters system apply various models of approximation parameters at the distributed lags. Such approach allows reducing number of estimated parameters of system. The Koyck scheme [2, 12], based on a change of factors of model on a decreasing geometrical progression is most widely applied. The Fisher model [1, 11] is based on a change of factors model on the set decreasing arithmetical progression. Fisher scheme are applied in that case when object parameters decrease from the first members of a progression. S. Almon [13] modified Fisher model, having applied the polynomial law of change factors. Other approaches to the definition of laws change parameters at the distributed lags are described in [4, 11, 14, 15]. The accounting of a priori information on dependence between the distributed lags in the form of some rational polynom is stated in [16].

The considered models of factors minimize number of unknown parameters. To an estimation of parameters apply a method least-squares method [1-4]. In these works the model structure is postulated a priori and the problem of parametrical identification is considered. In [17] the interactive algorithm of an estimation parameters static plant with the distributed lags is offered. The length of a lag is set and does not become any assumptions of interdependence between system parameters. The case of a piecewise monotonic change of parameters plant is considered. In a number of works methods of a choice maximum length a lag are offered. They are founded on application the statistics, the rests based on the analysis [1, 15, 18]. In [19, 20] various methods of an estimation parameters model with the distributed lag in a case of a priori set structure of model are considered. In [21] influence of a priori information, received from the analysis of the empirical data, on a choice of structure model with the distributed lag on an output variable is researched. Polynomial schemes for estimation parameters are offered. In work [22] are described algorithm of an estimation parameters model with the distributed lag. On the basis of results modelling the structure of model which explains a mismatch of model applied now in the American interest rate on federal funds is selected. In [23] process of inflation with the help autoregressive models is researched. The choice of length a lag is carried out on the basis of consecutive magnification delays and an estimation of adequacy the received model. The choice of length a lag is based on step-by-step increase in delays and an estimation of adequacy the received model. Then the Akaike criterion and Bayesian information criteria are applied and the solution is made on model structure. The case of a priori uncertainty concerning structure and plant parameters was not study.

In work [24] the review of existing approaches to construction of models of an econometrics is executed. The analysis is based on methodology general-to-specific. It is based on simplification of the general theoretical model for the purpose of its conformity to experimental data. The methodology is based on statistical modelling and application of known statistics for a choice of length a lag. Authors consider application of the given approach to construction of models both with the dynamic specification of lag, and with a lag in an independent variable. The combination of methods of modelling to application of various statistics is most widely applied to a choice of structure the distributed lag [for example, 25, 26, 27]. In the majority of works disadvantages of existing statistics are considered and the area of their application is underlined.

In work [28] the information-set approach to structural identification of systems with the distributed lag in case of an irregular input [29] is offered. It is based on the analysis of static structures (visual portraits), reflecting nonlinear properties of system in special structural space [29]. Algorithms of decision-making on the maximum length of the distributed lag are offered. Algorithms do not demand calculation of statistical criteria. The analogue of Durbin-Watson criterion for a considered case is offered.

In the given work the approach offered in [28] develops. Criteria of decision-making on length of the distributed lag on input and output variables of system are described. It is shown, that for structural identification of systems with the distributed lag sector sets [28, 30] are not applicable. The approach to parametrical identification of system in the conditions of uncertainty is offered.

Article has the following structure. At first the method of an estimation of degree of linearity of system is described. The following section contains the description of a method of reception of set of the data for an estimation of structure of the distributed lag. In the subsequent sections the received results are applied to a choice of length of a lag on the basis of input and output variables. It is shown that sector sets are inapplicable for a choice of structure of a lag. In final section the problem of identification parameters of system with the distributed lag is analyzed. Results of modelling are resulted.

• II.    Problem Statement

Consider plant yn =AnTUn+ξn, (1)

where y ∈ R is an exit; U ∈ R^k is the input vector which elements are limited, is limiting nondegenerate functions; n ∈ J = [0, N ] is discrete time, N <∞ ; X = X ( u ∈ U , y ) ∈ R ^m is a vector of the distributed lags on u ∈ U and y ; A ∈ R^k , B ∈ R^m are vectors of constant parameters; ξ ∈ R is a perturbation, | ξ | <∞ for all n ∈ J .

We believe, as u∈ U  (i= 1 k) and ξ ∈ R are ir- i,n         n              ,                    n regular functions of time.

For (1) the set of the measured values is known

I o = { y n , U n ∀ n ∈ J N }                             (2)

and map Γ: {U}×{y}  ∀n∈J describing an ob servable informational portrait [7, 29].

It is necessary I, Γ to estimate on the basis of analysis structure of system (1). It means that it is necessary to estimate degree of linearity and dimension of vector X n .

• III.    Estimation of Degree of Linearity System (1)

Consider restriction of an observable information portrait Γui ⊂ Γ I     ∀i=1,k and for every Γui con struct a secant

γ(y,ui)=aiui,n , where a are some real numbers.

Introduce set on (2) set of secants for Γ

S( U , y ) = { γ ( y , u i ) ∀ i = 1, k }.

Definition 1 [7, 29]. Field of structures S of system (1) name set of maps γ ( y , u ) : { u } → { y } ∀ i =1, k on Euclidean plane Ε

S S = S( U , y ).

Designate

Φ =[γ(y u ) γ(y u )    γ(y u )]T n γ yn , 1,n , γ yn , 2,n ,   , γ yn , k,n and consider the equation yˆn= ΨTΦn,                                      (3)

where vector ^{Ψ ∈ R k} define by means of a leastsquares method. Estimation Ψ exists on the basis of the suppositions made in section 2 concerning input U .

Completeness of system (1) in the field of structures S follows from the following statement [29, 31].

• Theorem 1. Consider a vector of informative variables U_n e R^k and a field of structures 5 _$ c S( U , y ) for (1). Then the field of structures S of system (1) is full, if

k

Z ^ = 1,                                 (4)

i = 1

where ^ is i -th element of vector T in (4).

The theorem 1 gives sufficient conditions of linearity (nonlinearity, collinearity) systems (1) on the set field of structures. If the condition (4) is fulfilled, that field S is full. Hence, S is a linear span of an exit system (1). Otherwise make a solution on presence of nonlinearity or collinearity (autocorrelation) in system (1).

Let k Z^ = X . i=1

Magnitude A ( T ) = X — 1 name level of nonlinearity of system (1) in parametrical space P_T = ( A , B ) . As the distributed lags are the multicollinearity reason in (1), then A ( T ) will accept small values.

e ke, u,, n = ks (e, U, n) = ---- .                                (6)

i , n

Generate set

I k = I k ^{( k} , e ) = { e n , ^k n , n ^e J N = ^[0, N ] } , ^k n =^k_eA, n .

Definition 2. Name p = ( k , e ) structural space of the system (1), allowing to identify structure of vector X .

On will order k on increase. Generate kv , N                      e,u ,n                                            q where kq = ks (e, up q), q e JN = [0, N]. As to every kq corresponds value ev receive

I q = { e q , k q , q e J N, } .

In p define map Г ^q _ek : { k q } ^ { eq } and structure S ^v  corresponding to it.

Now estimate structure X on the basis of the analysis I ^v and S ^v .

Such approach well works at an estimation of structure nonlinear static systems [7, 29]. For systems with the distributed lag it demands modification.

• IV.    Set for an Estimation of Structure of Distributed Lag

Consider at first a case, when X_n = X ( u, _n). Apply the approach, offered in [7, 29]. Generate set for an estimation of structure (1). Introduce a variable s_n = I^TU_n , where I e R^k is a unit vector. Apply model y^ = a_ss_n . Find parameter a_s e R from a condition

aˆs

Let e„ = Ус - y„ is a variable which contains the dan       s,nn ta about structure of a lag of system (1). As argument

X(Uj) use variable uln e U„ , which ensures maxi mum value of coefficient of determination r2 between e,u e and u . It is true and for y . As shown in [7, 29], set {e„, U; „} does not allow to solve a problem of structural identification. The given statement follows directly from this that the index in an inequality of Holder [32] for e is close to zero. Therefore introduce coefficient of structural properties (CSP) [7]

• V.    Decision-Making on Length of a Lag in ^{X ( u , n )}

Set I = { e ,u. } contains uncertainty N_r and N,„ . e , u        n    , n                                           L             Lg

N is an incomplete account of linear component system (1). N _Lg reflects influence of disturbance from the distributed lag. For an exception N [28] construct a secant for e n

У (e, u-) = a о + a1 u-, n , where a, a define as a solution of a problem (5).

Introduce new variable p, = e_n — у ( e , u ,) which does not contain N . For estimation N _Lg analyze set { ^p n , u , n } .

To reception of a tentative estimation of the maximum lag m apply algorithm CD from [28].

In work the set-functional approach to structural identification is applied. Therefore known methods of a choice length the lag, based on statistical criteria (section 1 see), we do not consider.

To an estimation of independence of elements of a vector X apply the theorem 1. As the set analysis I is inefficient to eat apply results of section 4 and generate set

d =

N

E ■ n=1

.

I e , k x = { ⁵ п , ^k e , x„ ,i = 1, m ^V n ^{e J} N } ,

N

E e2

n = 1

where к_е^_{х л} calculate on the basis of (6) and designate en = e _n , x n e X .

On I introduce transformation 5 , ^k x

^Г , k _£ , xi : ^{{ k} _£ ,X inn ^} ^^{s n ^} .

Г , in space P = ( k ,e ) corresponds structure ,k^k 5 , xi          ^{1              s , 5}      \ ^e , x t,n ⁷ /

S . Construct secants for S ^k e , xi ,^{5                                                            k} e , xi ,⁵

Y ^{( e} n , ^ks ,x i,_n ) = PK x i,_n   V z = 1, m * ,                  (8)

where в are defined as the solution of a problem (5); m is a value m received by means of algorithm CD .

Generate a vector

Ф

5 , n

Y ^{( 5} n , ^kS, x in, ), Y ^{( 5} n , ^kS ,x 2, ,. ),

... , Y ( 5 , k_6I   )

^{n e} , ^x m *, n

and apply model 5_й = T T Ф_{5 n} to change forecasting 5 , where a vector T e R m define on the basis of results section 3.

Theorem 2 [28]. Let on set the Ie k field of secants is constructed for en

m _*

E ^W .... i * 1, i =1

where m. is defined by means of algorithm, CD_p ,

W e , i e^T 5 •

Remark 1. As 8_n contains the information on vector influence X_n at statistical treatment U_n , ^ use analogue of criterion Durbin-Watson criterion [28]

Level of nonlinearity of system (1) in the presence of the distributed lag on X define as

m _*

A ( T 5 )   V „ ,i - 1.

i = 1

Theorem 3. Consider the set of secants S£ set on Ie, kx , and a secant Y(e,k ,, ) = ak„ for S . Let for se-e,ui             1 e,ui                ke,u ,e cants coefficients of determinations are known r2   ,

• ^e , ^k xj

j = 1, m and r2k . Then the vector X(ut й) e Rm is an element of structure system (1), if Vz = 1, m

I r 2 k — r2k 1^ ^ ,

I e, kxz        e, kui I        x where ^ > 0 is a set value.

At the structure analysis the distributed lag of system (1) interpret as a nonlinear component (1). It follows from the theorem 1. Therefore develop the procedure, allowing making the decision on an uncertainty class N . More low the method of an estimation the distrib-

Lg uted lag, based on development of the approach from [28] is offered.

Between u_kn and u_iin_j (j >  1 ) is a dependence and disturbance works ^ . Therefore application of secants a linear class у can appear inefficient for decisionmaking. Consider set

• ¹    e , k x = { e n , ^k e , x p , n , P = 1, m ^V n ^{e J} N } ,             ⁽¹⁰⁾

where x p , n ^e X ⁽ u , n ^).

For every p = 1, m pair ( e_n , k_{e x}  ) will order on increase on k    and receive set

• ^e ’ ^x p , n

IV,k, ={ep,q, ke,x,,, q e JN}, xp                        p,q where the index p in ev is introduced to underline ■            p,q dependence eqv from kev,

Corresponding set Iv construct for u . Consider mappings

^Г Ve /{ e ; } ^ ( e p , q } • p >  1,                      (11)

Which describe structures Sv . For every Sv  cone, ep                     J      e, ep struct a secant

/ 2, p ⁽ e q , e p, q ) = a p,0 e q ⁺ a pl ⁽ e q )                       ⁽¹²⁾

and define a coefficient of determination r ²    .

² , e , e p

Theorem 4. Let for system (1) with X(u_{t n} e U_n ) e R m : i) on sets I ^v    and I ^v structures S ^v , described by

• ^e , k x p               k                           ^e , ^e p

mappings (11), are constructed; ii) for S ^v secants y^ Д e v , e v ₇)  (12) are defined. If for a secant

Yd ^( e V , e V „) structure the S v„   ( p >  1 ) condition is

* 2,p \ q    p,q /                              e,ep    N*        / executed

2,ev,eV        v , where 5 > 0 is some set number, then is x = u v                                                             p, n      l, n — p element of structure system (1).

The theorem 4 allows to define length of the distributed lag m * of a variable u . e U . The decision accept on the basis of the interdependence analysis between a virtual variable e and its forecast by means of variables x .

P , n

The decision on lag presence on u can be received on the basis of the analysis of the data in space p = ^{( k} , ^e ).

Consider set IV = {ev, k^, q e Jv} and define on it mapping Гve,^ : {kl,q }^{eqv} , where kVq is a coefficient of structural properties on an input u,. On a basis ГV,k set structure Sv . Generate sets Iv and on them de-e,k                                      e,k l’ fine ГV, and SY   , p > 1 . Define for SV,and e,k                    e,ke

’ xp                        ’ e, xp

S ^v secants

• e , k e , x p

v   v           vv    vv

• Y2 ( el,q , kl,q ) = Y2,i = al,0kl,q + al,1 (kl,q )  ,

  /2 (< -,, kV. -. ) = /2.,, = a;.,0 kL, + ■    k.V.,, )2,(14)

where alV0, alV1, avp,0, avp,1 are some numbers defined by means of least-squares method. For y2 (e^q, k^q ) and Yd (eV ., kV , j coefficients of determinations also are / 2 I xp ,q     xp ,q J known r2    , r2    . Designate average values x

2,Y2,i ,e ’    2,Y2,p,eV             °                     °                     p,n as xp,n

Theorem 5. Let for system (1) with X(ut n e Un) e Rm in space p = (k,e) : i) on sets IV k , IV structures Svek and S , described by mappings Г and Г , are , i                                                                                           , xp                          , constructed; ii) for S and S      secants (13), (14)

,l                          , e, xp are defined. If for a secant                 structure the

^{Y 2} \ x p , q ,    x p , q )

S^v_ek   ( p >  1 ) condition are executed

² , / 2, x _p , e^{V       2} , / 2, l , e^V

P

I a^V ,1 - x p , n | ^ ⁿ p ,

where 5_p >  0 and n_p are some set numbers, then is x_{p n} = u_{z n}__p element of structure of system(1).

The proof of the theorem 5 is obvious. It is based that structures S and S     describe variable change e .

• ^e , k l                 ^e , k e , x p                                                                 ^q

Therefore the decision on inclusion in structure of system (1) accept concerning that variable x_p e X_n , which ensures necessary level of a coefficient determination. Values r ²     should belong to the set interval, as re-

2,/2,p ,e flects (15). If values r2     are approximate, then use restriction (16) on a received estimation of average value xp,n = U,n—p .

Other approaches of a choice of length the distributed lag u are described in [28].

• VI.    Choice of Length Lag for X ( y ⁿ )

Let in system (1) X_n = [ x 1,n , x 1, n ,..., x_z , n f , where xi,n = Уп- и l = 1, l . To a prior estimation l apply algorithm CD . One of methods of a choice of length the distributed lag is described in [28]. It is based on application of the theorem 1. As show results of modelling, to make the decision on structure of the distributed lag on y_n in space p = ( k , e ) on a class of linear secants for virtual portraits S_{e , k} not always it is possible. Therefore we describe the approach based on application of theorems 4, 5.

Consider space p p =( eV,eV„), where eV,ex. n are el-s,e          q i,q                        q i,q ements of sets

I Vy, = { e ; . k :., q . q e J N } .

I V ,, = ( e v, ^{, k} :,., q e J N } , ^l > 1.

On I v , k , ,I V , k„ introduce mapping ^г V , e . : { e V j >  * e- vq } , i >  1. The method of its construction is described in section 5. Г v corresponds structure S v_D . For every e , e_i                                                                   e , e_i

Sv construct a secant e,ei v v         v v      v     v2

^Y 2, i ⁽ e q , e i , q ^{) —} a i ,0 e q + a i ,1 ⁽ e q ^{)                           (17)}

and define a coefficient of determination r ²   . Apply

2,ev,eiv the theorem 4 to an estimation of length the distributed lag on yn .

Consider space P k =(kv ,ev). On set Iv define s, xi ,e           e,xi                                      xi mapping Гvek : {kv $}>{ev} and a virtual portrait

Sv , where kv  is a coefficient of structural propere, e,xi                               i ,q ties on an input x . Also consider set

I V, k, ={eq, k,, q, q e JN}, introduce mapping Гv^: {kv^}>{ev} and structure Sev,k . Apply (13), (14) and define secants

Y 2 ( e q ^, k„. . ) = ^y = a , „k_m + <1 ( k .v,„, ) ^2,     (18)

y ( ^, i< q ) = z „= a ; ,. k ;„+ ^а 4 < ; „) .      d»)

where a ^v , a ^v , a ^v , a ^v are some numbers defined by means of a method least-squares method.

^For / 2 ( e q . ^kv . , . q ) ^and Y 2 ( e vq ^{: k} V . q ) coefficients ^of determinations also are known r ²    , r ²    . Desig-

2,72,e :    2,y2,i,e nate average values x as x . Apply the theorem 5 and receive an estimation of length the distributed lag on yn .

The offered approach apply in a case

X_n = X(u, n e U n , , n ) e R m .

It is possible to apply Lyapunov characteristic indicators to an estimation of the distributed lag [33]. For this purpose use the approach described in [28, 29].

• VII.    About Sector Sets

On the basis of the analysis of sector sets (SS) [29, 30] we can make the decision on a nonlinearity class. Despite complexities their construction for irregular inputs

SS allow to solve problems of structural identification of nonlinear static systems. Attempts to extend this approach on systems with the distributed lag have appeared unsuccessful. Explain it to that the distributed lag is result of the decision of difference equations. The received decision is somewhat approximate to a variable which is a basis for lag reception. Therefore SS in structural space for a base variable and its lags will differ not strongly. It does not allow developing effective algorithms of decision-making. Presence of the distributed lags on variables y , is the reason of decrease a coefficient of determination between input variables and a system output.

• VIII.    About Estimations of Parameters of System (1) at Distributed Lags

Identification of parameters in system with the distributed lags will execute on a class of a priori set models of parameters (look section 1). Such approach it is based on minimization of number of the estimated parameters in the conditions of a multicollinearity. It is the dominating. Authors offer various variations of approaches within the limits of the given concept of identification [17]. In [28] the method of identification the distributed lag on the basis of application Lyapunov characteristic indicators is described. It is based on estimations of a coefficient structural properties system on the set input. The coefficient structural properties is a parameter estimation at the considered distributed lag. Here we give development of the given approach.

We accept the received estimations of an average coefficient structural properties for admissible estimations of parameters at the distributed lags and form a vector B e R ^m . Introduce some limited vector 0e R h , where h <  m , 0e Q₀. In particular, at h = 1 ,

• ⁶ e^₀ = { ^ e R,0 e [ 1 - S h ,1 + E h ] } ,

^ >  0 is some set number. The second composed in the right part (1) write down in a form

B T X n = O B T X n .                            (20)

Apply a least-squares method (LSM) and receive an estimation 0 .

If adequacy of model with an estimation 0 is unsatisfactory, then choose h > 1 . Consider a vector 0 and execute division X into parts so that they contained nonsingular components. Let, for example Xn =[XTn,X2T,n]T . Then B = [BT,BT]T. Let e = [6l.62]T, d(0) = 0,ih, + O2ih_, where h + h2 = h , D(0) is a diagonal matrix from a vector 0, I^ e Rh1xh1 is an unity matrix, + is a direct sum of matrixes.

Then instead of (20) in model of identification for B^T X receive a relation

B T X n =[ ^ 1 B T , 0 B T ][ XL , X T n ] T .

To a vector estimation 0 apply LSM. Estimate adequacy of the received model. If the forecasting error appears is big, then change dimension of vector 0 . Execute identification process again.

Remark 2. A vector 0 is possible to identify by means of adaptive algorithm taking into account restriction 0 e Q₀ . To synthesis of procedure identification apply a method ф -algorithms [34].

• IX.    Examples

Consider system (1) with A = [1.5;2;2.8] ^T  ,

B = [0.7; 0.61 X n e R 2 , X n = X ( 4 n ). u ,-n e U n e R ³ are limited stochastic functions, ^ is a random variable with a zero expectancy and a final dispersion, | ^ | < 0.3 . u receive on a basis the decision difference the equations of the second order. Apply the theorem 1 and receive, that the system is nonlinear, A ( ^ ) = 0.03 . Value A ( T ) explain presence of linear interdependences (multicollinearity) in system. For lag estimation generate set

I e , u = { e , U i,n ( V i = 1,3 ) & ( V n e J ) } .          (21)

The analysis I has shown, that the lag is at a variable u . Apply algorithm CD and receive a prior estimation of length of a lag m . The estimation of length of a lag on u_u is m* = 2. To validation of the received result apply the theorem 4.

Generate sets Ive,k , Iv , consider mappings (11) and structures S;p , where p > 1. For S;p define secants e,ep                                             e,ep

Кp ^{( e}q , <, q ) ^and r ² e , e p :

• _{v v                  v                  v} 2      ₂

  / 2,1 ( ^e q , И, q )         ' q^q   ^U.U1 ^^( ^e q ) , r ₂ , ₍ /, _e ; = ⁰’⁹⁴⁸ ,

  / 2,2 ( e q , e Vq ) = 0.967 e q - 0.019 ( e q ) 2 , ^ ^ ,^ = 0.934 ,

  / 2,3 ( e q , e 3V,q ) = 0.954 e ; - 0.0038 ( e q ) 2 , r 2_e, , = 0.91 .

2, e , e ₃

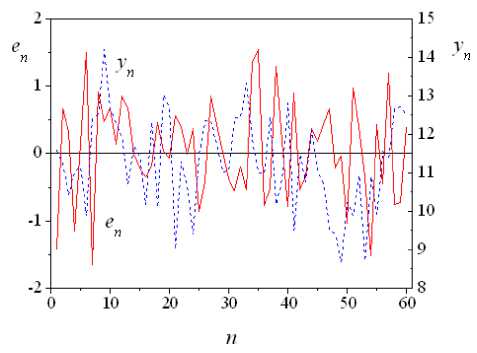
Fig. ^1: Change y n , £ n

Let 3 = 0.93 . Apply the theorem 4 and receive m* = 2. On Figure 1 show lag influence on u_{x n} .

To check of the received estimation of a lag apply theorems 5. Define secants (13), (14) and coefficients of determinations

/2 (^q , Кq ) = /2,1 = 2.13^q - 0.793 (k1qq ^ , r2_  , = 0.971,

2, / 2,1 , ^e 1

Y (eV „, k;q) = Yx = 1.93 kV q + 0.48 Uv; „)

2 x1 ,q      x1 ,q          2,x1                 x1 ,qx r2_   . = 0.964,

2,/2,^ ,e;’

Y (;^v k v = y

/2     x2,q ,   x2,q r2_ v = 0.928,

² , / 2,x 2 , ^e x 2

= 1.76kv  + 0.22 (k; q )2, x2 ,q                  x2 ,q

Y (e v ., k ; „)= y_lx = 1.69 k ;  + 0.053 (k ; _q )²,

2     x3 ,q     x3 ,q          2,x3                x3 ,q                    x3, r2_   ; = 0.922.

² , / 2, X 3 , ^e x3

Average values for u and x_p : u = 2.026 , X = 2.011 , x₂ = 1.996 , x₃ = 1.98 . Let 5_p = 0.043 , n_p = 0.02 . Check up conditions (15), (16). They will be executed for lags x , x . So, we have received estimations for length of the distributed lag on an input u .

On Figure 2 show results of application the theorem 5. They confirm a conclusion about influence of the distributed lag as some equivalent nonlinearity in system. This conclusion receives from the analysis of change secant Yu of structure SV^ . For /^ we have almost linear dependence that confirms an elimination of a lag x of model structure.

Consider system (1) with Xr = |^,n,x2 n] , ,„ = Уп-1,x2,n = U\,n-1. Execute the analysis of set (21) and apply algorithm CD to an estimation of the dis- tributed lag. Results of the analysis give lags on y and uY n. The estimation is m* = 1 on these variables. Apply the theorem 4 and confirm this conclusion.

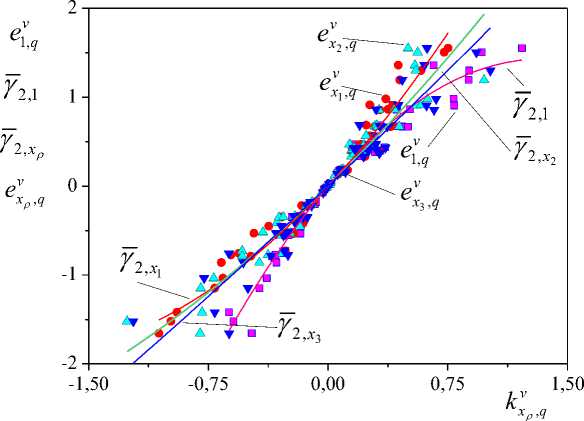
Fig. 2: Structures S^ and secants y.

Define secants (13), (14) and coefficients of determinations

72 (eVq, kv,q ) = 72,1 = 1.909kq - 0.567(kVq )2, r2_  , = 0.933 ,

² - 7 2,1 , e 1

/ к „, k* ) = 7ц = 2.0 kv + 0.771 kX2\

• 2    x2 ,q     x2 ,q         2,x2             x2 ,qx

r²_   , = 0.965,

2,/,

2, x ₂ x ₂

/ (e V „ k ") = 7ц  = 1.694 k ^; „ + 0.115( k ^; J,

2     x _2,2 , q     x ₂ , q         2, x _2,2                  x _2,2 , q                   x _2,2 , q

'   — -V

2, ⁷ 2 X 2,2 , e x 2,2

= 0.946,

where ^X 2,2, q = ^u 1, q -2

Average values for u_x „, x ₂„ and x _{2 2} „ : u_x = 2.028 , X₂ = 2.023 , X₂₂ = 2.0 . Secants / 2,1 , / ₂ , _x corroborate lag presence on u_x „ . The secant / 2, _{X j} is almost linear (for a linear secant / 1 _x   r ²_     v = 0.944). Condition

■ 2,2      2, 7 1x22 , ^e x 2 ,2

• (16) for Y _v with n = 0.15 is not true. Therefore 2, ^X 2,2                P

x is no element of structure of system (1). High

• r ²     v explain by means of application of the state-

• 2,71,2,2 ,ex2,2

ment from [28]. Similarly execute identification of the distributed lag on y .

So, results of modelling confirm efficiency of the offered algorithms and methods.

• X.    Conclusion

In work is functional-set approach to structural identification of discrete systems with the distributed lag is offered. The decisions on structure lag system part accept on the basis of the analysis special static structures. It is shown that the distributed lag can be considered as nonlinearity. We have applied to decision-making on length of a lag secants of the second order and have made the analysis of change their parameters. It is shown, that as criterion of decision-making on a belonging of the distributed lag the system structure can use degree of linearity of a secant the second order. The approach to parametrical identification of factors model is offered at the distributed lags. Unlike existing approaches we do not do any assumptions concerning the law of change parameters. The approach is based on definition of tentative estimations parameters model on the basis of the analysis of a coefficient structural properties system. These estimations are specified on the basis of identification auxiliary factors (multiplicate parameters). Results of modelling have confirmed working capacity of the offered methods and algorithms.