Structural transformations of incoming signal by a single nonlinear oscillatory neuron or by an artificial nonlinear neural network
Автор: Roman Peleshchak, Vasyl Lytvyn, Oksana Bihun, Ivan Peleshchak
Журнал: International Journal of Intelligent Systems and Applications @ijisa
Статья в выпуске: 8 vol.11, 2019 года.
Бесплатный доступ
Structural transformations of incoming informational signal by a single nonlinear oscillatory neuron or an artificial nonlinear neural network are investigated. The neurons are modeled as threshold devices so that the artificial nonlinear neural network under consideration are systems of nonlinear van der Pol type oscillatory neurons. The neurons are coupled by synaptic weight coefficients to endow the systems with the configuration topology of a chain or a ring. It is shown that the morphology of the outgoing signal – with respect to the shape, amplitude and time dependence of the instantaneous frequency of the signal – at the output of such a neural network has a higher degree of stochasticity than the morphology of the signal at the output of a single neuron. We conclude that the process of coding by a single neuron or an entire chain-like or circular neural network may be considered in terms of frequency modulations, which are known in Physics as a way to transmit information. We conjecture that frequency modulations constitute one of the ways of coding of information by the neurons in these types of neural networks.
Nonlinear neuron, artificial nonlinear neural network, coding of information
Короткий адрес: https://sciup.org/15016611
IDR: 15016611 | DOI: 10.5815/ijisa.2019.08.01
Текст научной статьи Structural transformations of incoming signal by a single nonlinear oscillatory neuron or by an artificial nonlinear neural network
Published Online August 2019 in MECS
Construction and implementation of mathematical models that yield a high degree of protection of information are among present challenges of cryptography. Models that feature significant changes of the structure of the incoming informational signal are of special interest. In this paper, we study transformations of an incoming signal by a single oscillatory neuron as well as by a system of nonlinear oscillatory neurons coupled by synaptic weight coefficients. These coefficients are chosen to endow the artificial nonlinear neural network with the topology of a chain or a ring. The interaction between the neurons is assumed to be of “dipole – dipole” type. We show that the proposed models change the structure (shape, amplitude, frequency and phase) of an incoming informational signal in a significant way.
The structure of the article consists of 5 sections:
-
• The first section (introduction) indicates the need to build and implement mathematical models based on neural networks with nonlinear oscillatory neurons for cryptographic systems.
-
• The second section presents an analysis of scientific papers related to the transformation of the structure of input signals by a single neuron or neural network.
-
• The third section describes the purpose and method of studying the processes of morphology transformation of the input signal using a chain or ring network of nonlinear oscillatory neurons.
-
• In the fourth section, a mathematical model of the chain and ring network of nonlinear oscillatory neurons is constructed.
-
• The fifth section presents the solution of the mathematical model of the chain and ring network
of nonlinear oscillatory neurons and a computer experiment to transform the morphology of the input signals by a single neuron and a system of neurons. The results of studies of the criteria for the occurrence of resonance effects in a nonlinear oscillatory neuron are also presented. It is shown that resonance effects in a nonlinear oscillatory neuron occur under the condition that the frequency of the external non-stationary signal coincides with the intrinsic dynamics of the neuron. The coding of information on the basis of frequency modulation using a nonlinear oscillatory neuron is proposed. Decoding using the inverse operator, which acts on the vector of the output signal, is proposed.
-
II. R elated W orks
At the initial stages of processing of sensory data, wavelet analysis is an effective instrument in the determination of the informative component in the neural signals that are being registered. Usually this determination is performed by analysis of the structure of the point-wise processes, that is, analysis of the timefrequency dynamics of neural responses [1 – 8], in which the information is carried by the times at which impulses (spikes) are generated rather than the shape of these responses [9]. The mechanisms by which the spikes are generated are only partially understood [10], while the ways in which nonlinear oscillatory neurons transform the structure of an incoming information signal have not been investigated, to the best of our knowledge.
In [2 – 5, 8] the transformation of signals by a sensory neuron (threshold device) is analyzed; the analysis does not take into account the dynamics of the neuron itself. It has been shown, by means of classical models of threshold systems such as “integrate-and-fire” [2 – 4] and “threshold crossing” [5, 8], that different characteristics of complex dynamics at the input of a sensory neuron are preserved in the structure of certain pointwise processes [4 – 8], [11 – 14].
Numerical modeling of the dynamics of a neuron subject to a stationary external signal, without consideration of the threshold effect of the neuron, was performed in [15]. In contrast, in this paper we consider a model with nonstationary external signals, which are transformed by an artificial nonlinear neural network modeled by a system of nonlinear oscillatory neurons of van der Pole type. In this system, the neural connections are represented by synaptic weight coefficients that take into account the threshold effect of the neuron.
Using the technique of double wavelet analysis, the authors of [16, 17] investigate time-frequency dynamics of the sensory neuron (threshold device), while taking into account both its own dynamics as well as the dynamics generated by the action of a non-stationary external signal. The sensory neuron is modeled in [16,17] as a threshold device that transforms an incoming signal into a sequence of output impulses. This sequence of impulses was described by a sequence of Dirac delta functions, each function corresponding to the moment of generation of an impulse (spike). These model impulses have the same form and amplitude, thus the information about the external action of the dynamic signal is expressed only by the time intervals between the moments of the generations of the impulses.
The study of structural transformation of incoming signal by a nonlinear oscillatory neuron that has its own dynamics, as well as by an artificial nonlinear neural network that consists of such neurons, contributes to understanding of neural networks of human brain. Indeed, biological neurons of the brain generate waves of various frequencies [18 – 20], which are transmitted as incoming signals to other neurons. It is therefore important to understand the response mechanisms of the latter neurons, that is, hoe the outgoing signals are generated. The proposed study can also be applied to development of coding algorithms that feature high degree of protection of information as well as to recognition of multispectral images.
-
III. S etting O bjectives
In this paper we investigate, by means of an analytical-numerical method, the processes of transformation of the structure of the incoming signal by a single oscillatory neuron, taking into account its threshold effect, as well as an artificial nonlinear neural network represented by a system of neurons that are van der Pol type oscillators coupled by synaptic weight coefficients. The weight coefficients are chosen to endow the neural networks with the configurational topology of either a chain or a ring.
-
IV. M athematical M odel
We consider decoupled as well as coupled systems of nonlinear oscillatory neurons.
In the case of a system of N decoupled neurons, the k - th sensory nonlinear oscillatory neuron Xk ( t ) is of van der Pol type – a threshold device – such that its own dynamics is described by the parameters ц > 0, ^k (the own frequency of the k - th neuron) as well as pk (the amplitude parameter of the k - th neuron), see Fig. 1. The system reads
X k + Ц [ X k - / М N 0 k ; Na )] X k + M , \; = V(t ) (1)
where p2(N3 k; Nck) = p2k tanh( N0k 2 Nck) with Nо k, NCk ^k and <72 being the number of the incoming impulses, the threshold number of impulses of the k - th neuron and the dispersion, respectively, V(t) is the external incoming informational signal, while for each k = 2,3,..., N
V k ( t ) = X k - 1 ( t ) (2)
is the incoming non-stationary signal on the k - th oscillatory neuron. Note that V ( t ) equals Xk ч ( t ) , the latter being the result of transformation of the external signal V ( t ) by k — 1 previous neurons.

Fig.1. Schematic representation of the process of transformation of an incoming signal V ( t ) by a sensory nonlinear oscillatory neuron (threshold device). The moments of time at which impulses are generated at the output of the threshold device Xk ( t ) correspond to the moments of time at which the threshold level is crossed.

Fig.2. Schematic representation of an artificial nonlinear neural network with the topology of a chain and one-sided connections manifested by weight coefficients X k 4 , where k = 1,2,..., N .
Note that ^ = 0 .
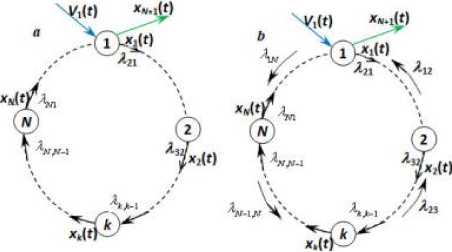
Fig.3. Schematic representation of an artificial nonlinear neural network with the topology of a chain and (a) one-sided connections manifested by weight coefficients X k_x and XNX or (b) two-sided connections manifested by weight coefficients \k_p Xk_x ^, XNX and \N , where k = 1,2,..., N.
In the case of a coupled system of N nonlinear oscillatory neurons, we assume that the neurons are related among themselves by synaptic weight coefficients Xjk , with the topology of a chain (Fig. 2) or a ring (Fig. 3). This artificial nonlinear neural network is described by a system of nonlinear differential equations
X k + M k ^ X k + X X X
—
P k ( N 0 k ; N ck» X k + -" X k - X ^ ik X j = V ( t )
where the "dot" denotes differentiation with respect to the time-variable t,k = 1,2,...,N and all the other functions and parameters of the system are defined as above. We assume that X^ = 0. The desired topology of the artificial nonlinear neural network is achieved by an appropriate choice of the weight coefficients. For example, if ^ = 0 for all j, k such that j ^ k +1, where X n+i = Xi, the k — th equation of system (3) involves only the dependent variables X and X , where X is identified with X , so that the neural network has the topology of a ring, see Fig. 3(a). If, in addition, Xi = 0 , the ring is broken, and the network has the topology of a chain, see Fig. 2. In the case where ^ = 0 for all j, k that satisfy j £ {k — 1, k +1}, the system has the topology of a ring, with two-sided links between consecutive neurons, see Fig. 3(b).
In both cases, the nonlinear oscillatory neurons X in systems (1) and (3) can generate impulses even if the external non-stationary signal is absent (V (t) = 0) , provided that the number of the impulses N present in the sensory neuron exceeds the threshold value N , that is, N0k > Nck. Indeed, in this case, pk (N0k,Nck) > 0 [18]. Therefore, each nonlinear neuron X can be considered as a threshold device that transforms the incoming non-stationary signal V (t) (which arrives at the k — th neuron) into a sequence of impulses at the output (see Fig. 1). This effect is due to the overlay of the dynamics of the incoming non-stationary signal with the own dynamics of the neuron. Due to the latter dynamics, the structure of the signal at the output of the k — th nonlinear neuron is significantly changed in comparison with the incoming signal V (t) .The complex dynamics of the transformation of the incoming non-stationary signal is discussed in [18].
Possible applications of neural network technologies include detection of multispectral images, detection and recognition of computer attacks, compression of input images [21 – 23].
In the next section, a three-neuron system that models an artificial nonlinear neural network with ring-like topology is studied. The Krylov-Bogolyubov-Mytropolsky method of subsequent approximations utilized for numerical solution of this system is summarized. Several incoming informational signals are considered: a single rectangular impulse, a superposition of several rectangular impulses, a superposition of products of periodic signals times a Gaussian functions. Plots of the output informational signal and of the frequency modulation of the incoming signal due to its modification by the appropriate artificial nonlinear neural network are provided.
V. E ncoding via an A rtificial N onlinear N eural N etwork with one or T hree V an D er P ol T ype O scillatory N eurons
In this section we consider a coupled system of 3 oscillatory neurons described by system (3) with N = 3 with chain-like topology (see Fig. 2), which reads
X 1 + ^ 1 [ X 2 - p ’ ( N 01 ; N c 1 )] X 1 + m 2 X 1 = V (t )
X 2 + M 2 [ X 2 - p 2 ( N ,2 ; N c 2 )] X 2 + < X 2 = X 1 ( t ) (4)
X з + M 3 [ X 3 2 - p ’ ( N 0 3 ; N c 3 )] X 3 + < X 3 = X 2 ( t )
where
X = X + ^x X2
X2 = X 2 + Д2 X + з. X (5)
X3 = X 3 + ^3 X2
iterative process for determining a(k n ) ( t ) and yk n ) ( t ) :
dak _ „(n-1).. 17ann-1) V „/(n-П „2 2 (n-1) 1 v(n
, = -ak W (ak ) sin Vk -pk cos ^k +---Vk cos^k dt Lx 7 J dV. = m0k + MkT(akn-1) )2 sin2 vkn - Pk21sin vkn cos vkn --33- Vksin dt Lv 7 J ^k a (k1
We solve system (4) by Krylov-Bogolyubov-Mytropolsky [24] method of iterative approximations. Below we summarize the method for the case of the decoupled system (1), for the sake of clarity. The application of the method to system (4) is done by an analogous procedure.
In system (1), we set
where n = 1,2,... and p k = p k ( N 0 k , Nck ) as in (1).
Let us discuss the choice of the initial approximations a k 0)( t ) and V (0) ( t ) in the iterative process (11). Take an average of the right-hand side of system (11) with respect to the interval [ 0,2 n ] using the rule from [17]:
<Ф>= ^Г Ф ( ^ ( n ) ) d V kn ) (12)
2 n J0
For the initial (zeroth) approximation, the expressions for the functions a ( 0)( t ) and Vk 0 (t ) are found from the following decoupled system of equations:
da (0)
dt
—i
' ak0) Mk
( a k ”)’
—
pk 2
X k n ) ( t ) = a kn )(t ) sin v kn )(t ) (6)
V n \t ) = m k t + ф к n ) (t ) (7)
d< dt 0k .
where n = 1,2,... is the iteration number and a(k n ) ( t ), ф ( n ) ( t ) are functions of the time variable t chosen so that (6) satisfies the k - th equation in system (1). We require that a ( t ) is a "slow-changing" function, that is,
The following two particular solutions of the last system (14) are chosen as the initial approximations in the iterative process (10):
ak 0)( t ) = -T=’ p== (15)
V1 + e - p k M kt
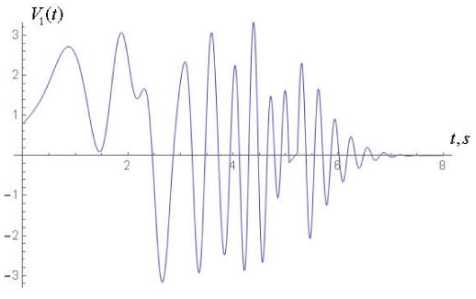
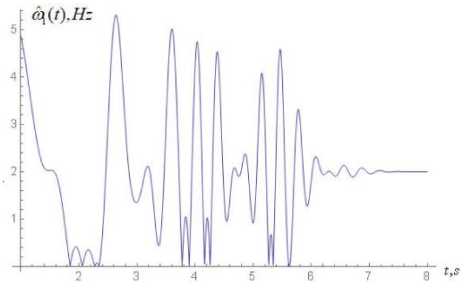
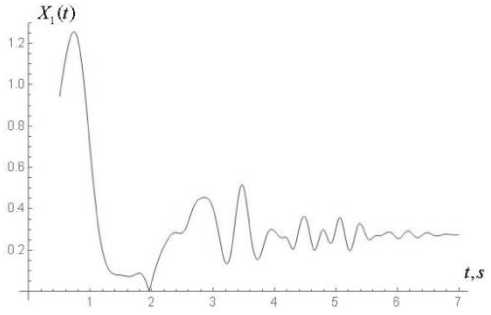
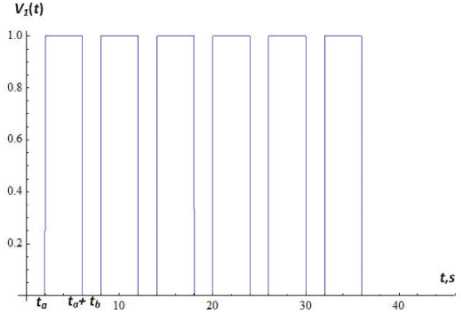
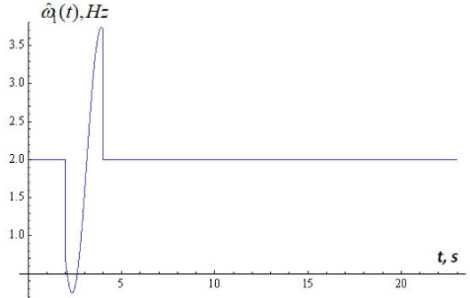
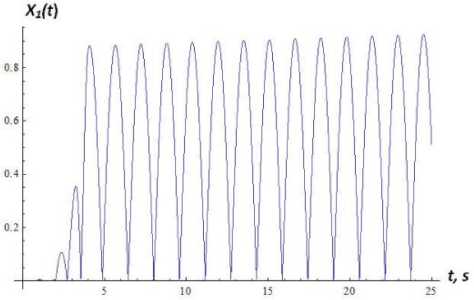
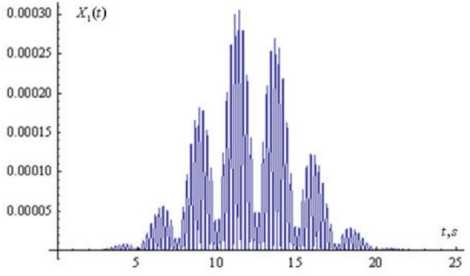
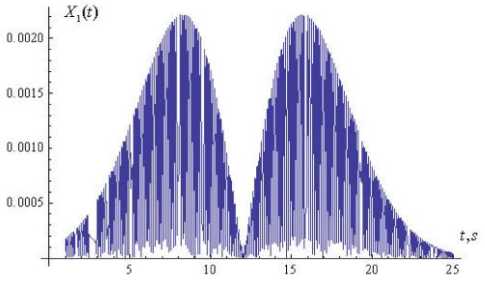
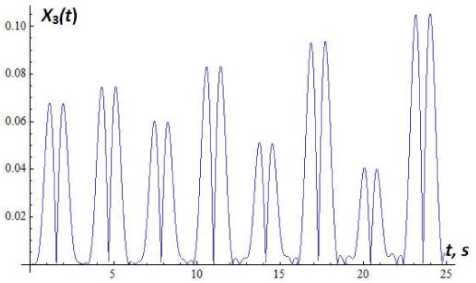
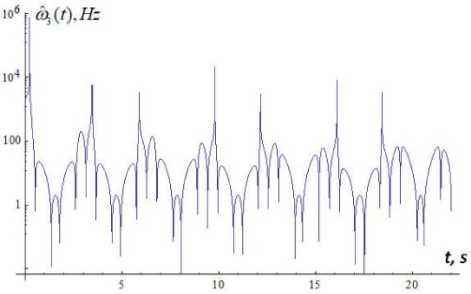
lim ak" vT(t) = m0 kt (16) Because substitution of (6) into the k - th equation of system (1) results with one differential equation for two unknown functions a(n) (t) and Vn) (t), we impose an additional condition Xkn) = m kakn )(t) cos vkn )(t) (9) where the function a(0) (t) satisfies the criterion (8) of slow changing function. To find expressions for a(1) (t) and vF(t) in the first approximation (n = 1) , expressions (15), (16) are inserted into system (11). Upon integration, the approximations a(1)(t) and V^Xt) are obtained. And so on. The iteration process terminates if the following conditions are satisfied: which is equivalent to a(nn) (t) sin V(n) (t) + a(nn) (t)V(n) (t) cos V(n) (t) - am cos ykn) (t) = 0. Upon substitution of (5) into the k - th equation of system (1), taking into account condition (10), applying an iterative procedure idea, we obtain the following akn,( t) - a” З t) ak(n)(t) < 8, V^(. t) - vk” "1)( t) vkn)( t) for all k = 1,2,...,N and for all t from the interval on which the solution of system (1) is sought, where 8 is the desired accuracy (in the subsequent examples, 8 = 10-5). System (4) of three nonlinear differential equations is solved by a similar procedure using the Krylov-Bogolyubov-Mytropolsky method [24] and the method of subsequent approximations. More precisely, at the initial step system (4) is solved without taking into account the synaptic weight coefficients 2jk . The solutions of this special case of system (4) are then set to be the initial approximation of the solution of (the most general form of) system (4). In the subsequent iterations, the solutions of the preceding approximation are inserted into the summands that contain the weight synaptic coefficients of system (4). Once conditions (17) are satisfied, the iteration process is terminated and X(n) (t) given by (6) is accepted as an approximate solution of system (4). As an example, we choose the external non-stationary signal VY (t) o be the sum of L simple non-stationary signals, each centered at the point t = t£ and characterized by the system of parameters M , see (21). More precisely, L-1 V( t) = £ 21 v, 1( t -1() + 2 (18) t = 0 where the functions v are the incoming simple signals. Each among the latter functions may be chosen to be, for example, a product of a Gaussian curve and an oscillatory function: operator [f n ] transforms the incoming signals weighed by the coefficients 2i and feeds them into the activation operator [f ] , see Fig. 4. In the case of decoupled system (1), for the k - th sensory nonlinear oscillatory neuron, the activation operator has the following form: [ fa. ]k = dr + И [X2 - P2 (N0k; Nck)] d + « (22) where k = 1,2,...,N. Fig.4. The structure of artificial nonlinear oscillator neuron (сoding scheme). v1( t- ^) = exp (t -1, )22 cos(« (t - tz)+a) The non stationary signal V (t) given by (18) and (19) is described by the system of parameters M 0 =(2*1) (20) m£ = (21«, t£,t ,a), 1 ^ l, (21) where each 2i is the weight coefficient representing the connection of the simple signal v with the neuron Xx (t); 2i is the weight coefficient of the signal shift; « is the external frequency of the oscillations that bear the information in the incoming signal, in Hz; t is the center of localization of the signal with respect to time, in seconds; т is the length of the characteristic time interval of the signal localization, in seconds; a is the initial phase, in radians. Formula (18) describes the superposition of the incoming signals (19) that arrive with the weight coefficients 2i at the input of the first neuron (incoming operator), with the the shift signal 2* . The input sum The output signal of the k - th nonlinear oscillatory neuron, see Fig. 4, is the output signal of the output operator [ fouД , for which the input is the output of the activation operator [f ] . The output operator [ fout L is necessary for the representation of the state of the neuron by values within a desired range. In the majority of literature this last operator is not emphasized and the output signal of the neuron is assumed to be the output of the activation operator [f ] . However, for the purpose of analysis and synthesis of artificial neural networks that have different activation functions with different domains and ranges, it is necessary to take the output operator [fouJ into account. Therefore, the nonlinear operator of transformation of the vector of incoming signals into the vector of the output signal can be written in the following form: X1(t) = [ fw ] ([ fa ] ([ fm ] (V, 2))) (23) Xk (t) = [ L. ]k ([ fa ]k ([ L ]k (Xk-1 (t)))), k = ^ N (24) where v = (^>1,...,^) and 2 = (2)1,...,2l1 ). By choosing different values of the parameters M , see (21), one can construct a theoretical model that adequately represents real physical (or biological) processes, which occur as the external non-stationary signal interacts with the own dynamics of the physical (biological) nonlinear neuron. Fig.5. The morphology of the external non-stationary signal V(t) that is a superposition of five simple signals. The signal V(t) is given by (18), (19) with L = 4, the weight coefficients V = V = 4 , V = 0 , the centers of localization of the simple signals t£ = 1 + £ , the lengths of time-intervals of localization т = 0,5s and the frequencies ^ = 8-, and the initial phases a = 0, I = 1,2,3,4. Fig.6. Time dependence of the instantaneous frequency ^ (t) of the bearing informational signal Vx (t) plotted in Fig. 5; ^ (t) = given by the second equation of system (11). dv®(t)is dt Fig. 5 shows the graph of the external non-stationary signal V (t) with L = 4. This signal is a superposition of five simple non-stationary signals v01= +1 and v^ , I = 1,2,3,4 given by (19), each arriving at the first sensory oscillatory neuron with the same weight coefficient V = 4 of connection with the first neuron and with the same length of the time-interval of localization given by т = 0,5s. The peak of the Gaussian curve in each signal v^ is chosen to be at t£ = I +1. The frequencies ^ of each simple non stationary signal Vx (t -t^) increase linearly with respect to the index I 4 so that ^ = —. This graph, together with the frequency modulation graph in Fig. 6, shows the moments of time at which local frequencies arise and represents the transitional stages of the transformation of the frequency spectrum of the signal. The instantaneous frequency ^ (t) of the informational signal Vx (t) is given by . dy^1(t) ^ (t) = —; it is given by the second equation of system (11). The comparison of the morphology of the informational signal in Fig. 5 at the input of the first nonlinear oscillatory neuron with the morphology at the output of the same neuron, see Fig. 7, shows that the structure of the incoming signal V(t) is changed significantly due to the interaction of the internal dynamics of the neuron with the external signal V(t). Fig.7. The morphology of the signal at the output of the first nonlinear oscillatory neuron X(t), the input signal being V(t) plotted in Fig. 5; Xx (t) is the solution of system (1) with N = 1 and the parameters px = 0,4, ^ = 0,1 and ^01 = 2. Fig.8. The bearing incoming information signal V(t) in the form of a superposition of rectangular impulses, each of the width 4s; the period T = 6s. The signal Vx (t) is given by (25) with L = 6, V = 1 for all £ = 0,1,...,15; ta = 2 and tb = 4 ; it arrives at the first nonlinear oscillatory neuron. The graphs of the external non-stationary signal V(t) in the form of a superposition of rectangular impulses and a single rectangular impulse are presented in Fig. 8, 9. Recall that the signal V(t) arrives at the input of the first nonlinear oscillatory neuron. The signal plotted in Fig. 8 is given by t( t) =£ Л1 {e [ t-((Z + 1) ta + tb) )]-9 [ t-(t + 1)( ta + t) )]} v ,(t - t, ) + ^ =0 where 9 is the Heaviside step function defined by 9(t) = 0 if t< 0 and 9(t) = 1 if t > 0. van 1л. 0J8 0j6 ■ 0.4 • 02 - t, 5 10 15 20 Fig.9. Bearing incoming information signal in the form of a single rectangle, with the impulse width of 2s. The signal V(t) is given by (25) with L = 1, \x = 1, ta = tb = 2; it arrives at the first nonlinear oscillatory neuron. Fig.10. Frequency modulation g\ (t) of the signal V (t) plotted in Fig. 9. Fig.11. Morphology of the signal X(t) at the output of the first oscillatory neuron, if the input signal V(t) is the rectangular impulse plotted in Fig. 9. The signal X(t) is the solution of system (1) with N = 1 and the parameters px = 0,4, ^ = 0,1 and ^ = 2. Fig. 10 provides the graph of the frequency modulation of the external signal V(t) plotted in Fig. 9. This graph shows the moments at which local frequencies arise as well as the transitional stages of the transformation of the frequency spectrum of the signal. Fig. 12 shows the morphology of the signal at the output of a single nonlinear oscillatory neuron modeled by equation (1) with px = 0,4, ^ = 0,1 and the frequency ^x = 0,2n , where the external signal V (t) = vxl (t - tx) and the parameters Mx =(3,4n,12,3,0) , see (18), (20). This morphology depends on the way the external signal interacts with the own dynamics of the nonlinear oscillatory neuron. Fig.12. Morphology of the signal X(t) at the output of the first oscillatory neuron, if the input signal V (t) = vxx (t - tx) and the parameters M1 = (3,4n,12,3,0) , see (19), (21). The signal Xx (t) is the solution of system (1) with N = 1 and the parameters px = 0,4, ^ = 0,1 and ^x = 0,2n. Fig.13. Morphology of the signal X(t) at the output of the first oscillatory neuron, if the input signal Vx (t) = vxx (t - tx) and the parameters Mx = (3,4n,12,3,0) , see (19), (21). The signal Xx (t) is the solution of system (1) with N = 1 and the parameters px = 0,4, ^ = 0,1 and toox = 4n. Suppose now that the frequency of the single nonlinear oscillatory neuron from the last example is modified to ^x = 4n, which coincides with the frequency ^ = 4n of the external signal V (t) = vn (t - tx) , see the list of parameters in Fig. 12 and (19), (21). Under this parameter regime, see Fig. 13, we observe a sharp amplitude rise of the output signal X(t) compared to the output signal in Fig. 12. Thus, a resonance effect takes place if the own frequency of the single neuron coincides with the frequency of the external signal. Fig.14. Morphology of the signal X(t) at the output of the neural network with ring topology and two-sided connections in Fig. 3(b) modeled by system (3) with N = 3 that consists of three nonlinear oscillatory neurons. The input is the harmonic signal Vx = V cos tot , Vo = 1 , to = 3 and the parameter values are ю01 = to02 = to03 = 2 , Pi = 0,4, p2 = 0,3, p3 = 0,2, ^ = 0,1, и = 0,2, и = 0,4, ^ = ^3 = 0,5, ^2 = ^3 = ^2 = 0,4. Fig.15. Frequency modulation of the output informational signal X(t) plotted in Fig. 14, in semi-logarithmic scale. Next, we consider the case where a harmonic signal arrives at the input of a three-neuron van der Pol type artificial nonlinear neural network with the morphology of a chain with two-sided connections (as in Fig. 2, but with two-sided connections). Wavelet analysis [25 – 27] of the morphology of this signal, see Fig. 14, shows that the structure of the output signal in this nonlinear network has a higher degree of stochasticity – with respect to the form, amplitude and the time-dependence of the instantaneous frequency of the bearing informational signal (Fig. 15) – compared to the signal at the output of a single neuron. This is related to the following feature of the three-neuron chain-like nonlinear-neuron network considered here: The structure (form, amplitude and frequency modulation) of the informational signal X(t) at the output of the ring is influenced not only by the synaptic connections between the nonlinear oscillatory neurons, but also by the interaction between the own, internal dynamics of each neuron with the dynamics of the signal that arrives at that neuron. To recover (decode) the incoming signal V(t) from the output signal X(t), one may plug in X(t) in the third equation of system (3) with N = 3 to find V (t) = X^ (t) , then plug in X2 (t) into the second equation of the same system to find V2 (t) = Xx (t) and, finally, plug in X(t)into the first equation of the same system to obtain the bearing informational signal V(t). Of course, in order to decode the output signal X(t), one must know the parameters of system (3). The results presented here suggest the following conjecture: the process of coding of the information by a single neuron or a nonlinear neural network can be considered in terms of the frequency modulation. Indeed, frequency modulation is known as one of the ways to transmit information. Therefore, it is expected that frequency modulation is one of the ways that neurons encode information. VI. Conclusions Based on the frequency modulation approach, a nonlinear model of coding of information is presented. The model encodes incoming informational signals via a network of nonlinear oscillatory neurons with the topology of a chain or a ring. The neurons in the network are connected by synaptic links. The decoding of the signals at the output of the linear chain and circular chain networks is performed using a simple process of substitution of the output signal into a system of ODEs (note that it is not necessary to solve the system to decode the signal, only to substitute it into the equations of the system successively). The chain-like and the ring-like networks of nonlinear oscillatory neurons connected via synaptic links are described by nonlinear systems of ordinary differential equations, with quadratic nonlinearity of the unknown functions near the first derivative. A method of solution of such systems of ODEs is proposed, based on the method of Krylov-Bogolyubov-Mytropolsky and the method of subsequent approximations. It is observed that in both kinds of networks the nonlinear oscillatory neurons play the role of frequency modulators. That is, the neurons modulate the instantaneous frequency of the incoming non-stationary signal that arrives at their input. It is shown that the structure of the signal at the output of the linear network (of nonlinear neurons) has a higher degree of stochasticity – with respect to the form, amplitude and the time dependence of the instantaneous frequency – compared to the morphology of the signal at the output of a single neuron. Existence of resonance effects in chain-like networks is demonstrated, under the condition that the frequency of the incoming nonstationary signal equals the frequency of the own, internal dynamics of the neuron. Acknowledgment This work was supported in part by the grant “Ontology based methods and means of construction of decision making support systems” (PI V. Lytvyn), Ministry of Education of Ukraine.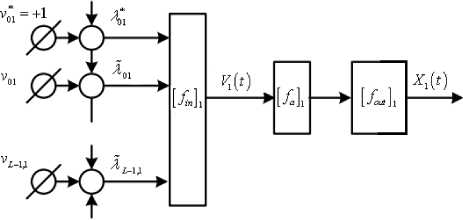
Список литературы Structural transformations of incoming signal by a single nonlinear oscillatory neuron or by an artificial nonlinear neural network
- Sauer T. Reconstruction of dynamical systems from interspike intervals[J]. Phys. Rev. Lett., 1994, 72: 3811 – 3814.
- Marzantowicza W., Signerska J. On the interspike-intervals of periodically-driven integrate-and-fire models[J]. Journal of Mathematical Analysis and Applications, 2015, 423: 456 – 479.
- O. N. Pavlova A. N. Pavlov. Improving the quality of extracting dynamics from interspike intervals via a resampling approach[J]. Communications in Nonlinear Science and Numerical Simulation, 2018, 57: 221-230.
- Sangmin Song, Ji Ah Lee, Ilya Kiselev, Varun Iyengar, Josef G. Trapani, Nessy Tania. Mathematical Modeling and Analyses of Interspike-Intervals of Spontaneous Activity in Afferent Neurons of the Zebrafish Lateral-Line. Biophysical Journal, 2017, 112(3): 136a.
- Racicot D. M., Lonytin A., Interspike interval attractors from chaotically driven neuron models[J]. Physica D, 1997, 104: 184 – 204.
- Castro R., Sauer T. Correlation dimension of attractors through interspike intervals[J]. Phys. Rev. E 1997, 55: 287 – 290.
- Sauer T. Nonlinear dynamics and time series. Eds C. Culter and D. Kaplan. Fields Institute Communications. American Mathemtical Society, 1997, RI 11: 63 – 75.
- Hegger R., Kantz H. Embedding of sequences of time intervals[J]. Europhys. Lett. 1997, 38: 267 – 272.
- Castro R., Sauer T. Chaotic Stochastic Resonance: Noise-Enhanced Reconstruction of Attractors[J]. Phys. Rev. Lett., 1997, 79: 1030 – 1033.
- Jinming Liu, Jian Mao, Bin Huang, Peiguo Liu. Chaos and reverse transitions in stochastic resonance[J]. Physics Letters A, 2018, 382: 3071-3078.
- Pavlov A. N., Hramov A. E., Koronovskij A. A., Sytnikova E. Ju., Makarov V. A., Ovchinnikov A. A. Wavelet analysis in neural dynamics[J]. Advances of Physical Sciences, 2012, 182(9): 905 – 939.
- Tuckwell H. C. Introduction to theoretical neurobiology. Cambridge University. Press, Cambridge, 1998.
- Janson N. B., Pavlov A. N., Neiman A. B., Anishchenko V. S. Reconstruction of dynamical and geometrical properties of chaotic attractors from threshold-crossing interspike intervals[J]. Phys. Rev. E, 1998, 58: R4 – R7.
- Pavlov A. N., Sosnovtseva O. V., Mosekilde E., Anishchenko V. S. Extracting dynamics from threshold-crossing interspike intervals: Possibilities and limitations[J]. Phys. Rev. E, 2000, 61: 5033 – 5044.
- Pavlov A. N., Sosnovtseva O. V., Mosekilde E., Anishchenko V. S. Chaotic dynamics from interspike intervals[J]. Phys. Rev. E, 2001, 63: 036205.
- A. N. Pisarchik, G. Huerta-Cuellar, C. W. Kulp. Statistical analysis of symbolic dynamics in weakly coupled chaotic oscillators[J]. Communications in Nonlinear Science and Numerical Simulation, 2018, 62: 134-145.
- John S., Bay and Hooshang Hemami. Modeling of a neural generator with coupled nonlinear oscillators. IEE Transactions biomedical engineering V, 1987, 34: 297 – 306.
- T. Shimoia, K. Mizutanib, D. Kojimaa, Y. Kitamurac, K. Hottaa, H. Ogawad, K. Oka. Identification of oscillatory firing neurons associated with locomotion in the earthworm through synapse imaging[J]. Neuroscience, 2014, 268: 149 – 158.
- Pavlov A. N., Pavlova O. N. Applications of wavelet analysis in the study of the structure of pointwise processes[J]. Letters to the Journal of Technical Physics, 2006, 32: 11 – 17.
- Suhakov V. Y. Fundamentals of synergetics. Kyiv: Oberehy, 2001.
- Lytvyn V., Peleshchak I., Peleshchak R. The compression of the input images in neural network that use the diagonalization method for the matrices of synaptic weight connections[C]. 2nd International Conference on Advanced Information and Communication Technologies (AICT), 2017, 66 – 70.
- Lytvyn V., Peleshchak I., Peleshchak R. Increasing the speed of detection and recognition of computer attacks in combined diagonalized neural networks[C]. 4th International Scientific-Practical Conference “Problems of infocommunications. Science and Technolohy”, 2017, 152 – 155.
- Lytvyn V.V., Peleshchak I.R., Peleshchak R.M., Holoshchuk R.O., Detection of multispectral input images using nonlinear artificial neural networks[V]. 14th International Conference on Advanced Trends in Radioelectronics, Telecommunications and Computer Engineering, TCSET, 2018, 119 – 124.
- Bogolyubov M. M., Yu. O. Mytropolsky. Asymptotical methods in the theory of nonlinear equations. Moscow: Nauka, 1992.
- Bozhokin S. V. Continuous wavelet transformation and exactly solvable model for non stationary signals[J]. Journal of Technical Physics, 2012, 82: 8 – 13.
- Grossmann A., Morlet J. Decomposition of Hardy functions into square integrable wavelets of constant shape[J]. SIAM. J. Math. Anal., 1984, 15: 723 – 736.
- Chui C. K., Wavelets: a mathematical tool for signal analysis (SIAM Monographs on Mathematical Modeling and Computation). Philadelphia: SIAM, 1997.


