Структура автоматической системы управления беспилотным летательным аппаратом

Современное развитие авиационных технологий требует создания высокоэффективных систем управления беспилотными летательными аппаратами (БПЛА). Эти системы должны обеспечивать автономное управление в сложных и изменяющихся условиях. Важно не только разрабатывать теоретические модели, но и проводить практические расчеты, чтобы убедиться в работоспособности предложенных решений в реальных условиях [1, 2].

Целью данной работы является разработка, анализ и математическое обоснова- ние методов управления беспилотными летательными аппаратами (БПЛА), основанных на теоретической механике и динамике машин.

Теоретические основыПринцип наименьшего действия

Принцип наименьшего действия является фундаментальным в теоретической механике и утверждает, что траектория движения системы между двумя точками во времени t1 и t₂ такова, что функционал действия S минимален:

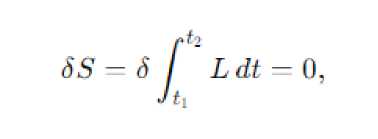
где L – лагранжиан системы, равный разности кинетической и потенциальной энергии:

L-T -U

Применение этого принципа позволяет вывести уравнения движения, описывающие динамику БПЛА, что критически важно для разработки алгоритмов управления.

Уравнения Лагранжа

Уравнения Лагранжа являются основным инструментом для вывода дифференциальных уравнений, описывающих дина- dt \9qj где qi — обобщенные координаты,    - обобщенные скорости.

Рассмотрим конкретную задачу. Пусть кинетическая энергия системы определя-

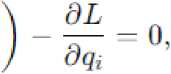
i — 1,2,..., n,

мическое поведение системы. Они выводятся из принципа наименьшего действия и имеют вид:

ется выражением           , а потенци-

(J _ альная энергия           . Тогда лагран жиан системы запишется следующим образом:

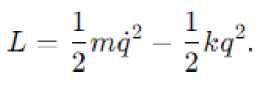
Подставляя этот лагранжиан в уравнение Лагранжа [2, 3], получаем:

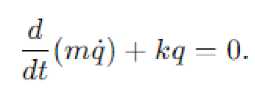
Решение данного уравнения описывает гармоническое колебание системы:

q(t) = Лсой(и;/ + ф), где co = J ^, a A и ф - константы, определяемые начальными условиями.

Методы оптимального управления

Методы оптимального управления направлены на минимизацию функционала качества, такого как затраты энергии или времени. Основой для этих методов являются уравнения Беллмана и принцип максимума Понтрягина.

Рассмотрим задачу минимизации функционала:

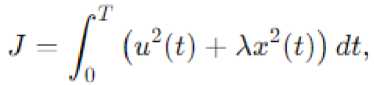
где u(t) – управляющее воздействие, x(t) максимума Понтрягина, записываем га-– состояние системы. Применяя принцип мильтониан системы:

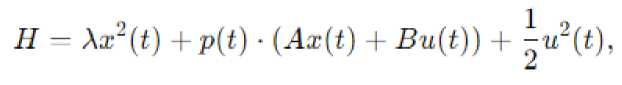
где p(t) – сопряженные переменные. Решение уравнений максимума позволяет

найти оптимальное управление:

НО - -,Н0-

Теория устойчивости Ляпунова Теория устойчивости Ляпунова используется для анализа устойчивости систе- мы [3]. Вводится функция Ляпунова V(x), которая должна удовлетворять следующим условиям: V(a) > 0, ЙО < От где –       производная функции Ля пунова по времени. Для системы, описываемой уравнением —    функция Ляпунова может быть выбрана в виде: где P – симметричная положительно определенная матрица. Производная по времени вычисляется как:

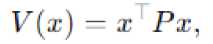
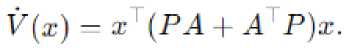
Если матрица РА + А1 Р отрицательно определена, система является устойчивой.

Математическое описание задачи управления

Задача управления БПЛА сводится к решению системы дифференциальных уравнений, описывающих динамику аппарата:

НО = /^GJ/^^i),

ИО = И® (0, «(0,0,

где x(t) – вектор состояния, u(t) – управляющие воздействия, f и g – нелинейные функции.

Для управления системой используется метод обратной связи по состоянию:

u(i) — —Kx(t), где K – матрица коэффициентов обратной связи, определяемая из условий устойчивости системы.

Заключение

В данной статье рассмотрены основные методы управления БПЛА, основанные на теоретической механике и динамике машин. Проведенный анализ и математические расчеты показывают, что предложенные подходы обеспечивают высокую точность и устойчивость управления, что критически важно для успешной эксплуатации беспилотных летательных аппаратов в реальных условиях. В дальнейшем планируется тестирование разработанных алгоритмов на моделях и в реальных полетных испытаниях.