Структура и электронные свойства кристаллов 3-12 фторографена

Двумерные соединения со слоевой структурой являются наноструктурированными материалами и поэтому их свойства отличаются от свойств трехмерных кристаллов [1]. Типичным представителем двумерных кристаллов является графен, который благодаря своим уникальным электронным свойствам может найти широкое применение в наноэлектронике [2]. Препятствием для этого является то, что монослои графена обладают металлической проводимостью. Для использования в электронных устройствах необходимо функционализировать графен так, чтобы его свойства стали полупроводниковыми [3]. Изменить электронные свойства графена возможно путем получения узких графеновых лент, пористого графена, полиморфных разновидностей графена и функционализации графена в результате химической адсорбции на его поверхности неуглеродных атомов [4-10]. Функционализировать графен возможно водородом, кислородом, хлором, фтором и другими атомами и молекулярными группами [7-10]. Наиболее перспективным является функционализация графена фтором, так как фторографеновые соединения обладают высокой термической устойчивостью [11, 12]. Диапазон изменения свойств графена при функционализации может быть существенно расширен в результате формирования различных полиморфных разновидностей соединений, отличающихся порядком присоединения неуглеродных атомов к слоям графена [13-19]. Кроме того, электронные свойства функционализированного графена могут сильно варьироваться при функционализации полиморфных разновидностей графена. Теоретически предсказана возможность существования множества полиморфов графена, таких как 4-8, 3-12, 4-6-12, 5-7 графен [13, 20, 21]. На основе этих структурных разновидностей графена возможно формирование множества полиморфов фторографена. Одним из наиболее интересных структурных типов фторографена является 3-12 фторографен, так как его свойства значительно отличаются от свойств фторографена, формирующегося в результате фторирования обычного гексагонального графена. Ранее структура и электронные свойства монослоев 3-12 фторографена были исследованы методами теории функционала плотности [17]. Однако в природе слоевые соединения обычно существуют в виде трехмерных кристаллов, состоящих из монослоев, упакованных в стопки. Так, кристаллы графита состоят из графеновых слоев, и получить отдельные слои графена удалось только в 2004 году [22]. Вероятно, при синтезе новых полиморфов графена фторографеновые соединения могут быть получены не в виде отдельных монослоев, а в виде трехмерных кристаллов, подобных кристаллам графита. Поэтому необходимы теоретические расчеты возможной структуры таких кристаллов и их свойств. В данной работе были выполнены теоретические исследования структуры и электронных свойств кристаллов 3-12 фторографена.

Методика расчетов

В качестве структурной модели для расчетов было принято, что кристаллы фторографена состоят из монослоев, в которых атомы углерода и фтора связаны между собой сильными ковалентными связями, а между слоями связи осуществляются силами Ван-дер-Ваальса. Расчеты трехмерной структуры кристаллов были выполнены при помощи специально написанной программы. В качестве метода расчета трехмерной структуры кристалла 3-12 фторографена был выбран метод атом-атомного потенциала, так как в отличие от других методов расчетов, он дает наиболее корректные результаты для описания ван-дер-ваальсовских взаимодействий, хорошо соответствующие экспериментальным данным [23]. Межатомные взаимодействия в методе атом-атомного потенциала описываются потенциалами, значения констант в которых определяется по эмпирическим данным. Для описания взаимодействий между парами углеродных атомов использовался потенциал Букингема, значения коэффициентов в котором были взяты из монографии А.И. Китайгородского [24]. Парные взаимодействия атомов фтора и атомов фтора и углерода рассчитывали при помощи потенциалов Леннарда-Джонса, численные значения коэффициентов для которых были найдены по экспериментальным данным о длинах межатомных связей и энергиях связей в различных C-F соединениях [25, 26]. При расчетах вычисляли полную энергию межатомных связей в кристаллах фторографена с варьируемыми параметрами структуры, в результате чего находили такую структурную конфигурацию, которая соответствует минимуму полной энергии межатомных связей. Так как энергия ван-дер-ваальсовых связей быстро уменьшается с увеличением расстояния между атомами (1/ R ⁶), то рассматривалось относительное расположение только пары соседних слоев в кристаллах фторографена. Вклад в полную энергию связи взаимодействия со слоями, расположенными на больших расстояниях относительно соседнего слоя, пренебрежимо мал. Так как слои имеют совершенную кристаллическую структуру, то расчеты выполняли для одной элементарной ячейки первого слоя, взаимодействующей с соседним слоем большого размера. В качестве величины, характеризующей энергию связи, вычисляли удельную энергию связи, приходящуюся на один атом. Размер соседнего слоя, хорошо описывающего слой бесконечного размера, был найден в результате предварительных расчетов, в ходе которых задавали различные размеры второго слоя: 0,4, 2, 4, 6, 8, 10, 20 и 30 нм. При слоях различного размера рассчитывали энергию межслоевых связей, в результате чего было установлено, что начиная с диаметра 10 нм, полная энергия связей практически не изменялась, поэтому в дальнейших расчетах диаметр слоя, с которым взаимодействовала элементарная ячейка, был принят равным 10 нм.

Примитивная элементарная ячейка 3-12 фторографенового слоя является гексагональной, однако для расчетов трехмерной структуры кристаллов в качестве элементарной ячейки была выбрана прямоугольная элементарная ячейка (рис. 1, а ), содержавшая 24 атома (12 атомов фтора, 12 атомов углерода). При расчетах методом атом-атомного потенциала было принято допущение, что структура слоев в кристаллах остается неизменной и возможно только изменение относительного расположения слоев. Координаты атомов в слоях были приняты равными соответствующим координатам, рассчитанным ранее для монослоев CF-L₃ _ ₁₂ [17]. Расчеты методом атом-атомного потенциала были выполнены в 3 этапа. На первом этапе находили межслоевое расстояние, соответствующее минимуму энергии связи при нулевом относительном сдвиге соседних слоев. На втором этапе межслоевое расстояние оставалось постоянным, при этом относительный сдвиг слоев варьировался (рис. 1, б) . Относительный сдвиг задавался вектором S , проекции которого на оси X и Y задавали в долях от векторов элементарных трансляций. Шаг изменения составлял 1/20 от вектора трансляции. Поэтому энергию связей вычисляли при 441 различном значении векторов сдвига. По полученным данным строили трехмерные и двумерные графики изменения энергии связи в зависимости от сдвига. Для нахождения значения вектора сдвига, соответствующего минимуму энергии связей, проводили ряд последовательных расчетов (4 шага) при

Беленков М.Е., Чернов В.М.,                              Структура и электронные свойства

Бутаков А.В., Беленков Е.А.                                  кристаллов 3-12 фторографена уменьшающихся в 10 раз на каждом шаге изменениях вектора сдвига. На третьем этапе при най- денном значении вектора сдвига, соответствующем минимуму энергии связи, варьировалось межслоевое расстояние, в результате чего была вычислена окончательная структура трехмерных кристаллов

.

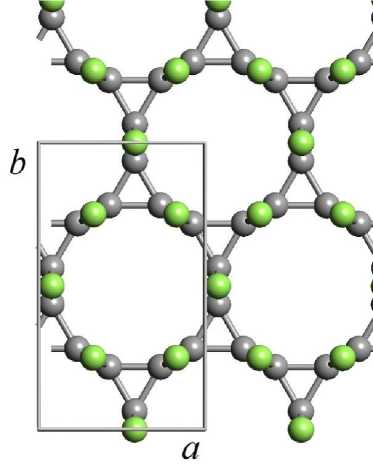
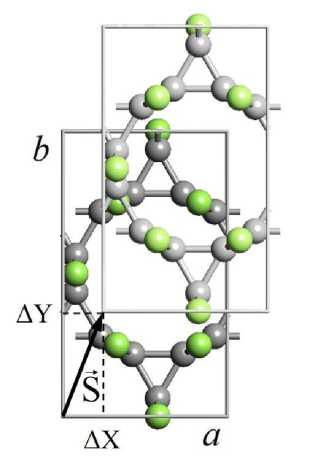
Рис. 1. Элементарная ячейка 3-12 фторографенового слоя (a) и схема задания относительного сдвига соседних слоев в кристаллах 3-12 фторографена ( a , b – векторы элементарных трансляций; S – вектор сдвига;

ΔX, ΔY – проекции вектора S на координатные оси X и Y соответственно; атомы углерода темно-серого цвета, атомы фтора светло-серого цвета)

Расчет электронной структуры и окончательные расчеты геометрически оптимизированной структуры кристаллов 3-12 фторографена были выполнены при помощи программного пакета Quantum ESPRESSO методом теории функционала плотности (DFT) в обобщенном градиентном приближении (GGA) [27–29]. В качестве исходной структуры брали орторомбическую элементарную ячейку 3-12 фторографенового слоя, координаты атомов в которой были найдены по итогам расчетов методом атом-атомного потенциала. При оптимизации структуры методом DFT-GGA межслоевое расстояние и параметр c были приняты постоянными. Варьировались только координаты атомов в элементарной ячейке и вектора трансляций a и b. При расчетах использовался набор из k -точек 12×12×12. Для разложения волновых функций использовался усеченный базисный набор плоских волн. Размерность набора базисных функций было ограничено значением равным 70 Ридберг.

(а)

(б)

Результаты и обсуждение

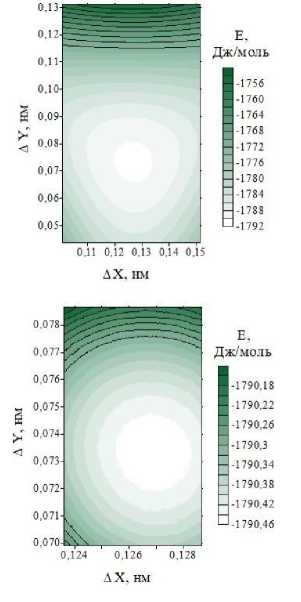
В результате расчетов методом атом-атомного потенциала было найдено значение межплоскостного расстояния при нулевом относительном сдвиге соседних слоев CF. Численное значение этого параметра составило 6,1411 Å. Удельная энергия ван-дер-ваальсовых связей, приходящаяся на одну молекулярную группу CF, составила –1613,94 Дж/моль. При найденном значении межплоскостного расстояния были рассчитаны энергии связей при различных значениях вектора относительного сдвига S соседних слоев. Графики изменения энергии межслоевых связей в зависимости от вектора сдвига приведены на рис. 2. Анализ рисунка показывает, что при сдвиге слоев энергия связи изменяется в широком диапазоне от –1613,80 до –1788,62 Дж/моль. Поиск относительного сдвига, соответствующего минимуму энергии связей, показал, что численное значение длины вектора сдвига составляет 1,4656 Å. Проекция вектора сдвига на ось X равна 1,2690 Å, а проекция на ось Y равна 0,7332 Å. Эти значения вектора сдвига были найдены при последовательном поиске с уменьшающимся шагом варьирования вектора сдвига, этапы которого изображены на рис. 2, в .

Структура кристаллов 3-12 фторографена была подвергнута дополнительной оптимизации методом DFT-GGA. Результаты выполненных расчетов приведены на рис. 3. Кристаллическая решетка кристалла относится к орторомбической сингонии. Расчетные значения длин векторов элементарных трансляций составляют: a = 5,046 Å, b = 8,739 Å, c = 11,516 Å. В элементарной ячейке содержится 48 атомов (см. рис. 3, а). Координаты атомов в элементарной ячейке приведены в табл. 1. Порядок нумерации атомов задан на изображении элементарной ячейки слоя (см. рис. 3, a). В элементарной ячейке кристалла содержится 2 монослоя CF-L3-12. Структура этих слоев остается подобной структуре изолированного слоя фторографена, и межслоевые взамодейст-вия ее не деформируют.

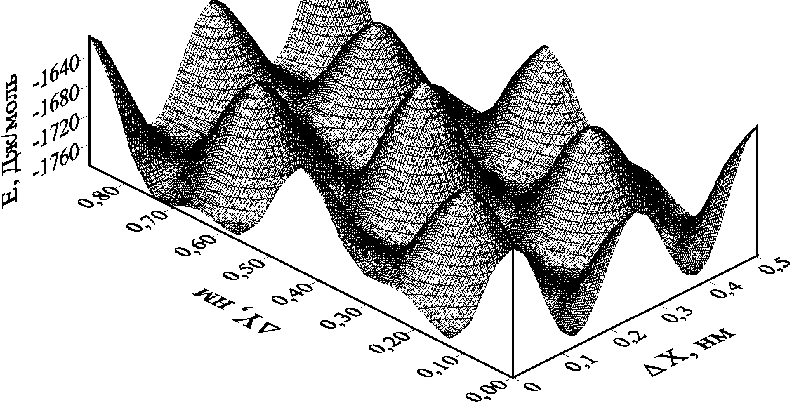
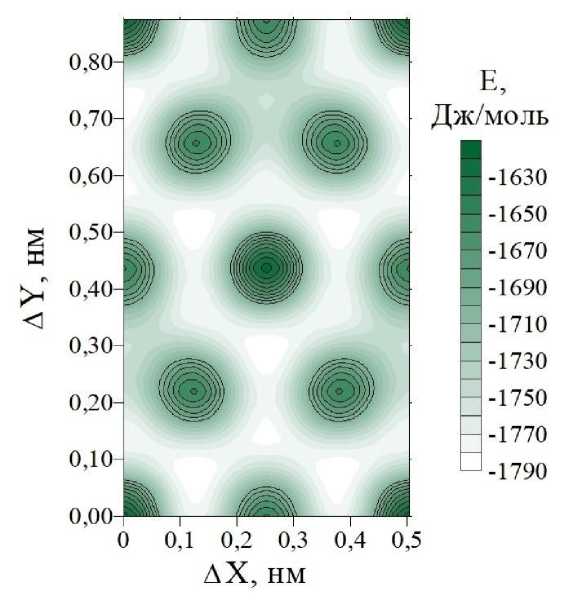
Рис. 2. Изменение удельной энергии E межслоевой связи, приходящейся на молекулярную группу CF при различных векторах относительного сдвига S (ΔX, ΔY) соседних слоев в кристаллах 3-12 фторграфена: (а) трехмерный график поверхности E = f (ΔX, ΔY); (б) двумерный график изоэнергетических линий поверхности Е спроецированных на плоскость сдвига (вектор сдвига изменяется в пределах элементарной ячейки)

(б)

(a)

(в)

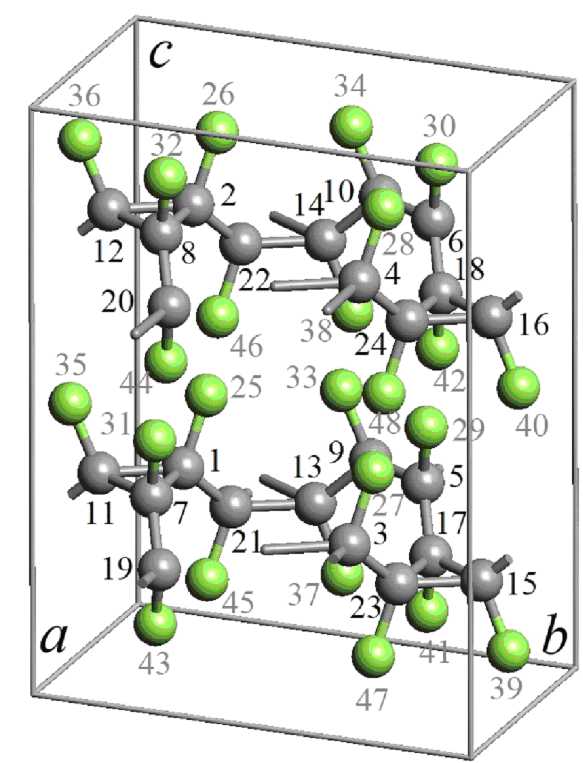
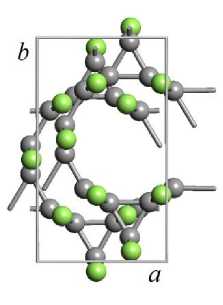
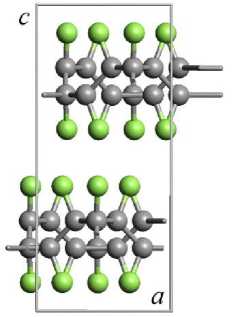
Рис. 3. Геометрически оптимизированная методом DFT-GGA структура элементарной ячейки кристалла 3-12 фторографена: (а) – нумерация атомов в элементарной ячейке; (б) – проекция на плоскость XY; (в) – проекция на плоскость XZ (атомы углерода темно-серого цвета, атомы фтора светло-серого цвета)

(б)

(а)

(в)

Соседние слои фторографена в элементарной ячейке кристалла сдвинуты друг относительно друга – рис. 3, б иллюстрирует относительный сдвиг слоев в плоскости XY. Слои сдвинуты так, что атомы фтора одного слоя располагаются напротив центра треугольной структуры из углеродных атомов. На рис. 3, в , изображающем сдвиг слоев в плоскости XZ видно, что атомы фтора соседних слоев располагаются достаточно далеко и между слоями нет зацепления, поэтому, вероятно, соседние слои в кристаллах фторографена должны свободно скользить друг относительно друга.

Структурные позиции атомов углерода и фтора в кристалле эквивалентные, поэтому структура кристалла характеризуется ограниченным числом различных длин межатомных связей и углов между ними. Эти параметры структуры приведены в табл. 2. Длины ковалентных связей L C-F между атомами углерода и фтора изменяются в диапазоне от 1,4083 до 1,4111 Å. Углеродуглеродные связи формируются двух типов: между атомами углерода в треугольных структурных группах L_C-C-1 и межатомные связи, формирующиеся между треугольными группами L_С-С-2. Углерод-углеродные связи первого типа варьируются от 1,5591 до 1,5630 Å, а второго типа – от 1,5094 до 1,5108 Å. Углы между C-F связями и соседними C-C связями близки к 109° (табл. 2). Углы между углерод-углеродными связями в треугольных структурных группах примерно равны 60°. Углы между C-C связями в треугольных структурных группах и связями соединяющими эти группы приблизительно равны 130°.

Таблица 1

Координаты атомов в элементарной ячейке кристалла 3-12 фторографена (нумерация атомов приведена на рис. 2, а ).

Атомы углерода				Атомы фтора
№	Х, Å	Y, Å	Z, Å	№	Х, Å	Y, Å	Z, Å
1	1,4465	1,5055	3,3963	25	0,9535	1,7781	4,6884
2	2,7989	2,2861	9,1494	26	2,3110	2,5739	10,4419
3	3,9693	5,8752	3,3963	27	3,4764	6,1478	4,6884
4	5,3217	6,6558	9,1494	28	4,8338	6,9436	10,4419
5	0,4849	5,8958	3,3917	29	0,9596	6,1674	4,6893
6	1,8369	6,6772	9,1385	30	2,3133	6,9585	10,4337
7	3,0077	1,5261	3,3917	31	3,4825	1,7977	4,6893
8	4,3597	2,3076	9,1385	32	4,8362	2,5889	10,4337
9	–0,2756	4,5347	3,3887	33	–0,2388	3,9763	4,6833
10	1,0785	5,3145	9,1487	34	1,1273	4,7606	10,4446
11	2,2473	0,1650	3,3887	35	2,2840	–0,3934	4,6833
12	3,6014	0,9448	9,1487	36	3,6502	0,3910	10,4446
13	–0,2761	3,4213	2,3674	37	–0,2396	3,9751	1,0713
14	1,0770	4,2032	8,1253	38	1,1219	4,7631	6,8316
15	2,2468	7,7910	2,3674	39	2,2833	8,3447	1,0713
16	3,5998	8,5729	8,1253	40	3,6447	9,1328	6,8316
17	1,4460	6,4507	2,3694	41	0,9529	6,1643	1,0817
18	2,7988	7,2321	8,1163	42	2,3088	6,9552	6,8253
19	3,9689	2,0810	2,3694	43	3,4758	1,7946	1,0817
20	5,3216	2,8624	8,1163	44	4,8317	2,5855	6,8253
21	0,4848	2,0595	2,3725	45	0,9558	1,7749	1,0733
22	1,8370	2,8410	8,1252	46	2,3131	2,5722	6,8265
23	3,0077	6,4292	2,3725	47	3,4786	6,1446	1,0733
24	4,3598	7,2107	8,1252	48	4,8359	6,9419	6,8265

Таблица 2

Рассчитанные (DFT-GGA) значения длин векторов элементарных трансляций (a, b, c), длин межатомных связей (L i ) и углов между ними (φ ij ) (* – минимальные значения, ** – максимальные значения)

a, Å	b, Å		c, Å	L C-F , Å	L C-C-1 , Å		L С-С-2 , Å
5,046	8,739		11,516	1,40833*	1,55914*		1,50935*
				1,4111**	1,56304**		1,51075**
φ F-C-C-1 , º		φ F-C-C-2 , º		φ C-C-C-1 , º		φ C-C-C-2 , º
109,335*		109,141*		59,895**		128,926*
110,757**		109,791**		60,1171**		130,21**

Зонная структура кристаллов 3-12 фторографена изображена на рис. 4. На уровне энергии Ферми наблюдается прямая запрещенная зона. Минимальное значение ширины запрещенной зоны наблюдается в точке Г, то есть в центре зоны Бриллюэна. Для отдельного слоя фторографена 3-12 наблюдалась аналогичная картина, то есть минимальная ширина запрещенной зоны наблюдалась также в точке Г. Однако ширина запрещенной зоны для кристалла и отдельного слоя существенно отличаются. В кристалле ширина запрещенной зоны составляет 3,03 эВ, что меньше примерно на 12 % чем в отдельном слое [18]. Кроме того, методом DFT-GGA была рассчитана полная энергия связей элементарной ячейки фторографенового слоя равная –19 203,58 эВ. На основе этой энергии была рассчитана удельная энергия сублимации как разница удельной энергии фторографенового слоя и энергий изолированных атомов углерода и фтора. Численное значение этой энергии составляет 13,83 эВ/(CF), что на 0,04 эВ больше энергии сублимации для отдельного слоя 3-12 фторографена [18].

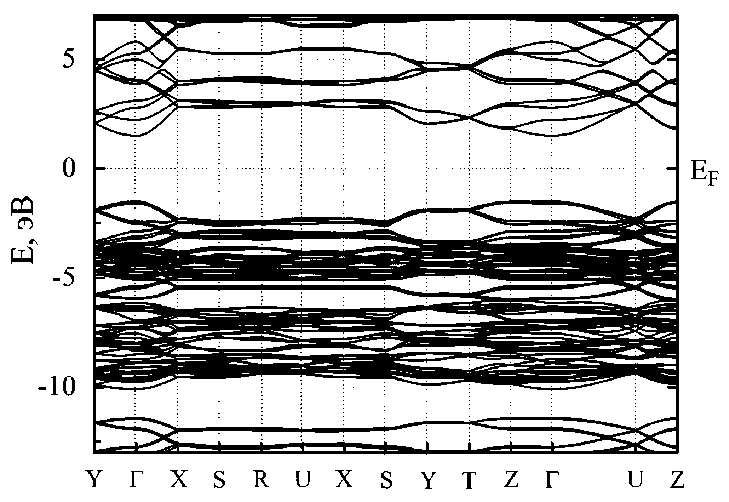
Рис. 4. Зонная структура кристалла 3-12 фторографена (за начало отсчета на оси энергий E принята энергия Ферми E F , ее расчетное абсолютное значение составляет –4,91 эВ)

Заключение

Таким образом, в работе методом атом-атомного потенциала рассчитана трехмерная кристаллическая структура кристаллов фторографена, сформированных из 3-12 фторографеновых слоев. Окончательная оптимизация структуры кристаллов CF-L3-12 и расчеты их электронной структуры были выполнены методом DFT-GGA. В результате расчетов установлено, что соседние слои в кристаллах фторографена должны быть сдвинуты на вектор S, компоненты которого равны ΔX = 1,2690 Å и ΔY = 0,7332 Å. Межслоевое расстояние, при котором наблюдается минимум энергии межатомных связей, составляет 6,1411 Å. Величина удельной энергии ван-дер-ваальсовых межслоевых взаимодействий, приходящейся на одной CF молекулярную группу, составляет –1613,94 Дж/моль. Энергия сублимации кристаллов 3-13 фторографена 13,83 эВ/(CF), а ширина запрещенной зоны 3,03 эВ. Численные значения этих параметров на несколько процентов отличаются от значений аналогичных характеристик для изолированных слоев CF-L3-12. Изменения свойств графеновых слоев функционализированных фтором при формировании трехмерных молекулярных кристаллов необходимо учитывать при создании многослойных гетероструктур, используемых в качестве элементной базы наноэлектронных устройств.

Исследование выполнено при финансовой поддержке РФФИ и Челябинской области в рамках научного проекта № 20-43-740015.