Структура оптимального интерполяционного пространства в интерполяционных тройках пространств p-суммируемых функций

В настоящей статье найден явный вид банахова пространства, которое является оптимальным интерполяционным пространством, как это понимается в [1], для некоторых интерполяционных троек пространств p-суммируемых функций.

Определение 1. Пусть A, B и C, D — две банаховы пары, E и F — промежуточные пространства между A и B , C и D соответственно. Тройка (A, B,E ) называется интерполяционной относительно тройки (C, D, F ), если для каждого ограниченного оператора из пары A, B в пару C , D его сужение на E является ограниченным из E в F .

Теорема 1 [1, с. 40] . Пусть E — промежуточное пространство для банаховой пары A , B , а C , D — другая банахова пара. Существует промежуточное для пары C , D пространство F(E ), обладающее тем свойством, что тройка A, B, E интерполяционна относительно тройки C, D, F тогда и только тогда, когда F(E ) С F.

Такое пространство F (E) называют оптимальным интерполяционным пространством.

Под пространством p-суммируемых функций будем понимать:

Определение 2. Пространством L p (0, + го ) p-суммируемых функций на полуоси [0, + го ) будем называть совокупность классов эквивалентности функций

f^(x) • k f k L i (G,+ ^ ) =

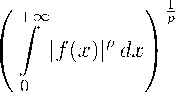
< + го .

Определение 3. Пространством Lp(a(x), (0, +^)) p-суммируемых функций на полуоси [0, +го) с весом a(x) > 0 будем называть совокупность классов эквивалентности функций

^f(x) • kf k L i (a(x),(G,+ ^ ))

+ ^              \ p

I I f (x) | ^p a ^p (x) dx j

G

< + ro .

(c) 2009 Ефимов А. И.

Для нахождения оптимального интерполяционного пространства воспользуемся теорией орбит, в частности, работой [3] Гуннара Спарра. Определим K -функционал так же, как и в [2]:

Определение 4. K -функционалом элемента x G A + B, где A, B — банахова пара, называется:

K (t,x; A,B)= inf {k x i k A + t k x 2 k B } , t> 0.

X=X 1 +X 2

Определение 5. K -орбитой элемента a G X i + X 2 в Y i + Y 2 называется

KOrb(a; (Xi,X2) - (Y^)) = L G Yi + Y2 : sup K(t,y;Yi,^) < +^1 , I                  t>o K(t,a;Xi,X2)         J где Xi , X2 и Yi , Y2 — две банаховы пары.

При этом можно рассматривать

K Orb(a; (X i ,X 2 ) - (Y i ,Y > ))

как банахово пространство с нормой

_     K(t,y; Y i ,Y > )

^kyk K^Orb(a)    sup K(t,a; X i ,X 2 ) •

Определение 6. Орбитой элемента a G X i + X 2 в Y i + Y 2 называется

Orb(a;(Xi,X2) - (Yi,Y>)) = {y G Yi + Y2 : (3T G L((Xi,X2), (Yi,Y2>>) Ta = y} , где Xi , X2 и Yi , Y2 — две банаховых пары.

Замечание 1. Пусть E — промежуточное пространство для банаховой пары X i , X 2 и a ∈ E. Тогда можно рассматривать

Orb(a; (X i ,X 2 ) - (Y i ,Y 2 ))

как банахово пространство с нормой kykOrb(a) = inf {kTIIl((Xi,X2),(Yi,Y2)) : T G L^Xi,^), (Yi,Y2)),Ta = ykakE} -

Далее будем рассматривать орбиту как банахово пространство с нормой || • k Orb(_a) -Определение 7. K (_{p 1} ,_{p 2} ) -функционалом элемента x G A + B, где A и B — банахова пара, называется:

K (p i ,P 2 ) (t,x) = K (p i ,p 2 ) (t,x; A,B) = Jxi f JH x ill A ¹ + tkx 2 k B } , t > 0.

В работе [3] было доказано:

Теорема 2 [3, с. 240-244]. Если Lp1a(X,^), Lp2b(X,^) и Lp1c(X,v), Lp2d(X,v) — две банаховых пары, где 1 6 pi, p2 < +ro, и x G Lp1a(X, ^) + Lp2b(X, ^), то y G Orb(x; (Lp^X,^, Lp2b(X,^)) — (Lpic(X,v), Lp2d(X,v)))

тогда и только тогда, когда y G KOrb (x; (Lpia(X, ^),Lp2b(X, ^)) — (Lpic(X, v), Lp2d(X, v))), где

L pa (X,^) = f^{(x) : kf} k L pa (X,_M) =

p

/ | f (x) | ^p a ^p (x) d^ I < + x

X

Лемма 1 [3, с. 236-237] . Пусть A - , A 2 и B - , B 2 —две пары банаховых пространств, тогда для любых 0 < p i , Р 2 < + x выполняется

K (p i ,P 2 ) (t,x; A i ,A 2 )

sup t>0 K(pi,P2)(t,y; B1,B2)

K (t,x; A 1M2 )

< x ° sup —-- < + x- t>o K(t,y; Bi,B2)

Для доказательства основного результата настоящей статьи нам потребуется несколько вспомогательных утверждений:

Лемма 2. Для любых чисел α , β и любых положительных чисел γ , δ справедливо неравенство

min(a,YA  a±7

V3 6) 6 в + 5 6 VP^)

Лемма 2 тривиальна. В частности, справедливость леммы очевидна, если неравенству (1) придать механический смысл. Пусть _β^α, ^γ_δ— координаты точек на числовой прямой, а в, 5 — массы этих точек. Тогда 0—2 будет координатой центра масс системы данных точек.

Лемма 3. Пусть a(x) > 0 Vx G (0, +x), p > 0. Для t > 0 введем множества

Qi(t) = Ix > 0 : a^p(x) > || ,   Q2(t) = (0, +x) \ Qi(t).

Тогда, если существуют интегралы

j If (x)lp dx и J If (x)|^pa^p(x) dx, Qi(t)                     Q2(t)

то

K(p,p)^(t,^f(x); Lp^{(0, +x)}, Lp

(a(x),(0, +x))) = у

If (x)I^pdx +t

Q1(t)

У If (x)|^pa^p(x) dx.

Q2(t)

<1 Непосредственно из определения следует

^K(p,p)(t,^{f (x)}; Lp^{(0, +x)} Lp^(a(x),^{(0, +x)))}

= inf f (x)=f1(x)+f2(x)

' +^

■ /^{|f(x)|p dx+}t o

+^

У If (x)|^pa^p(x) dx > . o

Легко заметить, что при этом инфимум будет ^{f (x)} = ^f1^{(x) + f}2^{(x) :}

fi (x) =

f (x) V x

0     Vx

достигаться на следующем разложении

^: a^p(x) > ¹,

: a^p(x) < -t

и

^f2^(x) = l⁰

I f (x)

V x : a^p(x) > -, V x : a^p (x)< -.

Тогда

K(p,p) ^(t, f^(x); Lp^(0,+^)^,Lp^(a(x),^(0, +^⁾⁾⁾

+^          +^

j |fi(x)|^pdx + t J |f₂(x)|^pa^p(x) dx

= j |f (x)|^pdx + t J |f (x)|^pa^p(x) dx. B Qi(t)                     Q2(t)

Следствие 1. Пусть функция a(x) > 0 монотонно убывает для любого x Е (0, +го). Тогда, если для любого положительного значения переменной x выражение tap (x) принимает значение меньше 1, то

K(p,p)^(t,^f(x); Lp^(0, +ГО), Lp^(a(x),^{(0, +}^)))

+^

= t У ^{|f (x)|p}a^p(x) dx = tkf(x)^(a(x),(0,₊^))

и

K(p,p)^(t,f(x); Lp^{(0, +}^L Lp^(a(x), ^{(0, +}^⁾⁾⁾ =

a ¹⁽tp )                  +^

j  If (x)|^pdx +t j

⁰                        a^-1( tp)

|f (x)|^pa^p(x) dx

в противном случае.

Следствие 2. Пусть функция a(x) > 0 монотонно возрастает Vx Е (0, +го). Тогда, если для любого положительного значения переменной x выражение t • a^p(x) принимает значение больше 1, то

+^

K(p,p)^(t,f(x);Lp^{(0, +}ro^),Lp^(a(x),^(0, +ro)))= j^|f(x)|pdx = kf^(x)kL_p(o,+^) 0

и a-1( tp)

K(p,p)(t,f (x); Lp(0, +^),Lp(a(x), (0, +^))) = j |f (x)|^pdx + t j |f (x)|^pa^p(x) dx ^a-1⁽tp)                       ⁰

в противном случае.

Лемма 4. Пусть E — промежуточное пространство для банаховой пары A, B , а C , D — другая банахова пара. Тогда пространство

F(E) = [ Orb(a;(A,B) ^ (C,D))

a∈E обладает тем свойством, что тройка (A, B, E) интерполяционна относительно тройки (C, D, F) тогда и только тогда, когда F(E) С F (т. е. F(E) — оптимальное интерполяционное пространство).

C Обозначим Orb(a) := Orb(a; (A, B) ^ (C, D)).

Пространство F(E) содержит все элементы вида Tx, где x E E и T E L(AB,CD). Значит, тройка (A, B,E) является интерполяционной относительно тройки (C,D,F(E)) и, если F(E) C F, то тройка (A, B,E) интерполяционна относительно (C,D,F).

По построению пространство F(E) состоит из элементов вида

У = ^yE 52 kyikOrb(ai) < +^А, yi = Tiai, Ti ^{E L(AB,}C^D). i         ai∈E

При этом будем считать, что kaikE = 1. Этого всегда можно добиться, так как из yi = T*a* следует yi = Tiai, kaikE = 1, где ai = ka^a* и Ti = ||a*kE • T*. Покажем теперь, что если тройка (A, B, E) интерполяционна относительно тройки (C, D, F), то F(E) C F.

По определению нормы в Orb(ai) найдется оператор Ti E L(AB,CD) такой, что kTi kL(AB,CD) 6 kyikOrb(ai) + ^•

Поэтому

52 kyikF = 52 kTiaikF ⁶ 52 kTikE^F kaikE = 52 HTikE^F

6 C X kTikL(AB,CD) 6 C X ^kyikOrb(ai) + ^^ = C ^1 + X kyi llorb(ai)^ < А и, следовательно, y E F. Таким образом, F(E) C F.

Лемма 5. Пусть Xi, X2 и Yi, Y2 — две банаховых пары и a E Xi + X2, a = 0, y E Yi + Y2, y = 0. тогда следующие утверждения равносильны:

K(t,y; Yi,Y2) ⁽ ) stup K(t,a; Xi,X2) (2)iim ^K(t,y; Yi,Y2) ⁽⁾t^o K(t,a; Xi,X2)

< + а ;

K(t,y;Yi,Y2)

< + А. и lim  ----——- < +ro.

t^+^ K(t,a; Xi,X2)

C Так как, согласно [2], K -функционал представляет собой положительную и непрерывную функцию переменной t > 0, то функция f = K (t,y; Yi,Y2)

f⁽⁾   K(t,a; Xi,X2)

также будет непрерывна для любого t > 0. Из сказанного следует, что на любом отрезке [ti,t2], 0 < ti < t2, функция f (t) является ограниченной.

Пусть выполняется первое утверждение. Предположим, что при этом не выполняется второе. Не нарушая общности рассуждений, можно считать г- K(t,y; Yi,Y2) lim f (t) = lim —;------------

= +а.

t^o ^{f ()}t^o K(t,a; Xi,X2)

Отсюда следует, что существует монотонно убывающая последовательность положительных чисел {un}n=i такая, что lim f(un) = +а.

n→∞

Поэтому

K(t,y; Yi,Y2)

⁽3 n ^EN) ^{f (}un) > sup —--- t>0 K ^(t, al Xi, X2)

что является невозможным, т. е. предположение о несправедливости второго утверждения привело нас к противоречию.

Пусть теперь выполняется второе утверждение, покажем, что тогда выполняется и первое. Обозначим

— K(t,y; Y1,Y2)                     K(t,y; Y1,Y2)

A = lim -хл--X—< ' ^ , B = lim лтл--x—тгг < +^, t^0 K(t,a; X1,X2)               t^+^ K(t,a; X1,X2)

тогда для фиксированного e > 0 существует h > 0 такое, что для любого t Е (0, h) выполняется f (t) < A + e и для того же самого e существует l > 0 такое, что при любом t Е (l, +го) выполняется f (t) < B + e. Кроме того, как сказано выше, 3 C > 0 : Vt Е [h, l], f (t) < C. Таким образом,

K (t,y; Y1,Y₂)

SUP              < max (A + e,B + e, C) < +ro, t>0 K(t, a; X1, X2)

что и завершает доказательство. B

Кроме того, так как функционал K(_p1,_p2) также представляет собой положительную и непрерывную функцию переменной t > 0, то дословно повторяя выкладки предыдущей леммы получим:

Следствие 3. Пусть Xi, X2 и Yi, Y2 — две банаховых пары и a Е Xi + X2, a = 0, у Е Yi + Y2, y = 0. Тогда следующие утверждения равносильны:

, х       ^K(pi,p2)^(t,y^{; Y1},Y²)

• ^{(1)    sup}К-----п-Х X \< ^х;

t>0 K(p1,p₂)^(t, a^{; Х}1^,Х2)

-- ^K(pi,p2)^(t, y^; YEY²)                 р-- ^K(pi,p2)^(t, y^; YEY²)

• (2)    lim ,---x---X—< ^xи  lim xx---x---X—<  ^x.

t^^{0 K}(pi,p2)^(t, a; ^X1^,X2)                ^t'' ^xK(pi,p2)⁽t, a; ^X1^,X2)

Лемма 6. Пусть f (x) > 0, g(x) > 0, h(x) > 0 при любом x > 0, и функции f (x)

и g(x) интегрируемы по Лебегу на интервале (0, v) для любого v > 0, а функция h(x)

непрерывная и монотонно убывающая на (0, +го). Если существует D > 0 такое, что для любого v > 0

vv j f (x) dx 6 D j g(x) dx,

то

vv

У f (x)h(x) dx 6 D У g(x)h(x) dx (V v> 0).

C Обозначим

A⁺(v) := {x Е (0, v] : D • g(x)

A-(v) := {x Е (0, v] : D • g(x)

-

-

f(x) > 0}, ^f(x)< ^0}.

Можно представить множества A⁺(v) и A (v) в виде следующих объединений измеримых множеств

A+(v) = (U A+(v) ) U B+(v) и A-(v) = (U A-(v) ) [ B-^ ii где

(V i) sup A+ (v) 6 inf Ai (v)

и

j (Dg(x) - f (x)) dx > J (f (x) - Dg(x)) dx,

A+(v)

A7(v)

а множества B⁺(v) и B (v) имеют нулевую меру. Тогда

h(sup A⁺(v)) У (Dg(x) — f (x)) dx > h(inf A-(v)) у (f (x) — Dg(x)) dx ^

A+(v)                                             A- (v)

j (Dg(x) — f (x))h(x) dx > j (f (x) — Dg(x))h(x) dx ^

A⁺(v)                                    A^-(v)

У (Dg(x) — f (x))h(x) dx > j (f (x) — Dg(x))h(x) dx ^

A⁺(v)                                    A^-(v)

• У f (x)h(x) dx + У f (x)h(x) dx 6 У Dg(x)h(x) dx + У Dg(x)h(x) dx ^

A^-(v)                     A⁺(v)                     A⁺(v)                       A^-(v)

vv

У f (x)h(x) dx 6 D j g(x)h(x) dx. B

Сформулируем основной результат работы и проведем его доказательство.

Теорема. Пусть a(x), b(x), d(x) — дифференцируемые монотонно убывающие на [0, +го) функции такие, что lim a(x) = 0, lim b(x) = 0, lim d(x) = 0 x^+^         x^+^         x^+^

a(0) = 1, b(0) = 1, d(0) = 1

и для каждого x > 0 справедливо b(x) 6 d(x) 6 1. Обозначим c(x) = d(b^-1(a(x))). При p > 1 тройка пространств

(Lp(0, +ro), Lp(b(x), (0, +ro)), Lp(d(x), (0, +ro)))

является интерполяционной относительно тройки

(Lp(0, +ro), Lp(a(x), (0, +ro)), F)

тогда и только тогда, когда

Lp(c(x), (0, +ro)) C F, где F — банахово пространство. Т. е. пространство Lp(c(x), (0, +^)) является оптимальным интерполяционным пространством.

• <1 Согласно лемме 4, оптимальное интерполяционное пространство можно рассматривать как сумму орбит

Orb(g(x) : (Lp(0, +го), Lp(b(x), (0, +го))) ^ (Lp(0, +го), Li(a(x), (0, +^))))

элементов g(x) пространства E = L_p(d(x), (0, +го)), которое для краткости обозначим S ^Orb(g^(x)) с нормой || • k^sо_гь(д(х)).

g(x)GE

Возьмем f (x) G L_p(c(x), (0, +^)) и покажем, что существует g(x) 6 L_p(d(x), (0, +^)) такой, что f (x) принадлежит орбите

Orb(g(x) : (Lp(0, +ro), Lp(b(x), (0, +ro))) ^ (Lp(0, +ro), Lp(a(x), (0, +^)))).

В качестве такого g(x) положим g(x) = f (a-1(b(x))) ((a-1(b(x)))0)p , тогда, так как lim a-1(b(x)) = +ro и lim a-1(b(x)) = 0, то x — ^                          x , ■ 0

k^g(x)kLp(d(x),(0,+ro))

^ |g(x)|^pd^p(x)dx 0

p

+^

j |f (a^-1(b(x)))|^p|(a^-1(b(x)))0| d^p(x) dx 0

1 ^p

+^

j If (t)|^pd^p(b^-1(a(t)))

k^{f (x)}kLp(c(x),(0,+^)),

т. е. g(x) G L_p(d(x), (0, +ro)).

Рассмотрим предел lim v→∞

+f |f (x)|pap(x) dx a-1(b(v))__________________________

J°|g(x)|pbp(x) dx

v

= lim v→∞

+^

R |f(a-W^M^a-W)))⁰dt

v

+^

R |g(x)|^pbp(x) dx

v

= 1.

А для предела lim v→∞

a^-1(b(v))

R    If (x)|^pdx

v

J^|g(x)|pdx

= lim v→∞

a^-1(b(v))

R    |f (x)|^pdx

a^-1(b(v))

R     If (t)I^pdt

= 1.

Согласно следствию

lim K(p,p)^(t,^f(x);Lp^{(0, +}^)^,L-p^(a(xR^(0, +^)) t^+^ K(p,p)(t, g(x); Lp(0, +ro), Lp(b(x), (0, +ro))

a ¹⁽_tp)                    +^

R   |f (x)|^pdx + t R   |f (x)|^pa^p(x) dx

V---                                a ⁽tP )

lim ------------------------------------------ v^^ b-1( tP)                +^

R |g(x)|^pdx + t R   |g(x)|^pbp(x) dx

^{0                         b-1(}tP)

a^-1(b(v))                              +ГО

R    |f (x)|^pdx +           R    |f (x)|^pa^p(x) dx

= lim v→∞

0                          vb^v) a-1(b(v))

^R|g(x)|^pdx + -/1= R |g(x)|^pb^p(x) dx

0                        b(v) v

Далее, используя неравенство леммы 2

min ^-^1 6 ^ 6 max ^,5), \в 6) в + 6       Vв s)

получаем

1 = min

a

lim v→∞

V a-

¹(b(=))

J    If (x)|^pdx

Л-----------;lim v           v→∞

J^{|g(x)|p dx}

+^

1=    J    ^|f(x)|pa^p(x) dx

b^(V) a—1(b(v))

+^

1=) / ^|g(x)|pbp(x) dx

/

6 lim v→∞

W))

^{J   |f (x)|}p dx ⁺"РЖ

0                          b(=)

J    If (x)|pap(x) dx a-1(b(v))

J |g(x)|p dx + 0

a^-1(b(v))

1=) / ^|g(x)|pbp^(x) dx

6 max

lim v^^

f ^{If(x)|p dx}

°; lim J ^|g(x)|pdx °° 0

1=   +Г If (x)|^pa^p(x) dx^

b^(V) a^-1(b(v))

Ри J Ig(x)I^pbp(x) dx b(=) ₌

= 1,

следовательно,

lim t^+^

K(p,p)⁽t,^{f (x)}; Lp^(0, ■ ^ )- Lp^(a(x), ⁽o,⁺^)) = 1

K(p,p)^(t,^g(x); Lp^(0, +Ю), Lp^(b(x), (° ⁺^))     ‘

Если же t стремится к нулю, то

limK(p,p)(t, f (x)^; Lp(0, +^),Lp(a(x), (0, +^)) t^⁰K(p,p)^(t,^g(x); ^lp^(0, ■ ^ '■ Lp^(b(x),^{(0, +}^))

Jim t^{kf k}Lp (a(x),(0,+^))= H^{f k}Lp(a(x),(0,+^)) t^⁰tkgkLp(b(x),(0,+^))      ll^gkLp(b(x),(0,+ro))

Тогда, согласно следствию 3, su K(p,p)(t1/(x)2Lp(01+ro),Lp(a(x)L(01+ro)) < t>0 K(p,p)(t,g(x); Lp(0, ^^БрО)^'),(0, +^)), а по лемме 1

K(t,f(x); Lp(0, +^), Lp(a(x),(0, +^)) < + t>0 к(t, g(x); Lp(0, +ro), Lp(b(x), (0, +ro))°°‘

Это означает, орбиты g(x).

что f (x) является элементом K-орбиты g(x), а по теореме [3] и элементом

Покажем теперь, что норма пространства |J Orb(g(x)) мажорируется нормой про-g(x)eE странства Lp(c(x), (0, +ro)).

Возьмем произвольный элемент

f^(x)G U ^Orb(g^(x)) g(x)GE

и

g(x) = f(a^-1(b(x)))((a^-1(b(x)))⁰) p.

Рассмотрим оператор T : g(x) ^ f (x), где f (x) — такая функция, что g(x) = f (a-1(b(x)))((a-1(b(x)))0) p •

Так как для норм выполняются следующие равенства:

+^         +^

kTg(x)kLp(0,+») = j If(x)lpdx = / If(a-W)))I^p(a-W)))'dx = kg(x)kL_p(o,₊„) 0                    0

и

+^

kTg(x)kLp(a(x),(0,+»)) = / If (x)|^pa^p(x) dx

+^

• = j If (a^-1(b(x)))|^p(a^-1(b(x)))⁰bp(x) dx = kg(x) k^)^)), 0

то оператор T является непрерывным как действующий из банаховой пары L_p(0, +го), L_p(b(x), (0, +^)) в банахову пару L_p(0, +го), L_p(a(x), (0, +^)) с нормой равной единице. Так как Tg(x) = f(x), то g(x) G E.

Тогда

Ilf ^(x)kS Orb(g(x)) 6 Ilf^(x)kOrb(g(x))

• ⁶k^T k^g(x)kE ^kL((Lp(0,+^),L_p(b(x),(0,+^))),(Lp(0,+^),Lp(a(x),(0,+^))))

(+^                               p

У If(a^-1(b(x)))|^p(a^-1(b(x)))⁰d^p(x) dx J = kf (x)kbp(c(x),(0,+^)).

Тем самым, доказано вложение L_p(c(x), (0, +^)) в оптимальное интерполяционное пространство.

Покажем теперь, что сумма орбит

Orb(g(x) : (Lp(0, +го), Lp(b(x), (0, +го))) ^ (Lp(0, +го), Lp(a(x), (0, +^))))

по всем g(x) G L_p(d(x), (0, +^)) вложена в пространство L_p(c(x), (0, +го)). Покажем, что для любой функции

g(x) G Lp(d(x), (0, +го))

орбита

Orb(g(x) : (Lp(0, +го), Lp(b(x), (0, +го))) ^ (Lp(0, +го), Lp(a(x), (0, +^))))

вложена в L_p(c(x), (0, +го)). Возьмем функцию f (x), принадлежащую орбите

Orb(g(x) : (Lp(0, +го), Lp(b(x), (0, +го))) ^ (Lp(0, +го), Lp(a(x), (0, +го)))), и сначала докажем, что f (x) G Lp(c(x), (0, +ro)).

то

Так как

K(t, f(x); Lp(0, +ro), Lp(a(x), (0, +ro))< + t>o K(t, g(x); Lp(0, +ro), Lp(b(x), (0, +^))      °⁰,

— K(p,p)^{(t,f (x)}; Lp^{(0, +}ro^),Lp^(a(x),^(0, -4-^)) t^~ K(p,p)^(t,g^(x);Lp^{(0, +}ro^),Lp^{(b(x), (0,} +ГО))

= lim v→∞

a-1(b(v))                                    + x

R    |f (x)|^pdx + 77= R    |f (x)|^pa^p(x) dx

0                         Vb^v) a-1(b(v))

^R |g(x)|^pdx + 7= R |g(x)|^pbp(x) dx

₀                       b(v) _v

< +ro.

Далее, используя, как и выше, неравенство

min ^.^ 6 a±2 6 max 77

\в 6у в + 6       \S’6y

справедливое для положительных чисел, приходим к выводу, что сходится, по крайней

мере, один из двух пределов

a^-1(b(v))

R    |f(x)|pdx lim --0----------- и v→∞ v

J |g(x)|^pdx

lim v→∞

+ OQ

|f(x)|^pa^p(x)dx

a-1(b(v))____________________ f |g(x)|PbP(x) dx

v

В первом случае получаем (3 Di > 0) (3 vo > 0) (V v > Vo)

v / o

|f (a ¹(b(x)))|^p(a 1(b(x)))0 dx 6 D1

v

|g(x)|^pdx.

o

Увеличив константу Di, можно добиться чтобы неравенство было верно для любого положительного v. Тогда, так как d(x) монотонно убывает и положительна, то согласно лемме 6 получаем V v > 0

v

v j |g(x)|pdp(x) dx o

I |f (a-1(b(x)))|p(a-1(b(x)))0dp(x) dx 6 D1 o или, переходя к пределу при v → ∞, kf (x)kLp(c(x),(0,+^)) 6 Di g('x' Lp.d.,x ,0, + x ■

Во втором случае a-1(b(u))

R    If (x)|pap(x) dx lim lim v→∞ u→∞

a^-1(b(v))

R |g(x)|^pbp(x) dx

v

Следовательно, (3 D2) (3 ug) (V u > v > ug)

uu j |f (a-1(b(x)))|pbp(x)(a-1 (b(x)))0bp(x) dx 6 D2 j |g(x)|pbp(x) dx.

Тогда, для любого измеримого множества A С (ug, +го) получаем

У |f (a^-1(b(x)))|^pbp(x)(a^-1(b(x)))0bp(x) dx 6 D₂У |g(x)|^pbp(x) dx. AA

Следовательно, почти всюду на интервале (ug, +го) выполняется

|f(a^-1(b(x)))|pbp(x)(a^-1(b(x)))0bp(x) 6 D2|g(x)|pbp(x) ^

|f(a^-1(b(x)))|^pbp(x)(a^-1(b(x)))⁰6 D2 |g(x) |^p^

|f(a^-1(b(x)))|^p(a^-1(b(x)))⁰d^p(x) 6 D2|g(x)|^pd^p(x).

Из этого следует, что u j If (a-1(b(v)))|p(a-1(b(v)))0dp(v) dv u0

a^-1(b(u))

u

6 D2 J |g(v)|^pd^p(v) dv, u0

u

j   If (x)lpcp(x) dx 6 D₂ У |g(v)|pdp(v) dv,

v0

u0

где vg = a ¹(b(ug)) и, переходя к пределу при и ^ го, получим

+^               +^

I |f (x)|pcp(x) dx 6 D2 I |g(v)|PdP(v) dv 6 D2kgkLp(d(x),(g,+^)) < +ro- v0

А для интеграла

u0

Z|f(_ТОdx 6

g

v0

j If (x)|^pdx =

g

6   1

ap(vg)

1 ap(vg)

/0|f(x)|PaP(vg) dx g

v0

j ^{If (x)|p}a^{p(x) dx 6} ap(vg)^kfkLp(a(x),(g,+^)) < ^+ro g

Это означает, что f (x) G Lp(c(x), (0, +ro)). Покажем теперь, что норма орбиты g(x) мажорируется нормой пространства Lp(c(x), (0, +го)), т. е.

³ C > ⁰ : k • kOrb(g(x)) ⁶ Ck • kLp(c(x),(g,+^)) •

Предположим, что это не так, тогда существует последовательность {уп}П=1 элементов пространства Lp(c(x), (0, +го)) такая, что kyn kOrb(g(x)) 6 ^n kyn kLp(c(x),(g,+^)) •

Обозначим

∞ f = X n=1

|yn | kyn kLp(c(x),(G,+^))

и проверим, что f является элементом орбиты

∞ kf kOrb(g(x)) 6 'V n=1

kyn kOrb(g(x)) kyn kLp(c(x),(G,+^))

∞

6 X- = 1.

2n n=1

При этом, kf kLp(c(x),(G,+^))

Iyn(x)|------Y cP(x) dx kynkLp(c(x),(G,+^)) /

∞

>X

n=1

/

G

yn(x' p kyn k Lp(c(x),(G, ■ ^))

cp(x) dx =

∞

X

n=1

^kyn ^kLp(c(x),(G,+^)) ^ky^{n k}Lp(c(x),(G,+^))

∞

X ¹ = +ro, n=1

т. е. f не является элементом пространства Lp(c(x), (0, +го)). Что противоречит дока- занному выше. Следовательно,

^ C > ^{0 :}k • kOrb(g(x)) 6 CII • kLp(c(x),(G,+^)) •

Поэтому справедливо вложение орбиты элемента g(x) в пространство Lp(c(x), (0, +го)). Тогда, согласно [1, с. 29–31], сумма орбит

Orb(g(x) : (Lp(0, +^),Lp(b(x), (0, +го))) ^ (Lp(0, +^),Lp(a(x), (0, +^)))), по всем g(x) Е L_p(d(x), (0, +^)) вложена в пространство L_p(c(x), (0, +го)). B