Структура течений в лабораторной модели общей циркуляции атмосферы

Общая циркуляция атмосферы играет ключевую роль при формировании погоды и оказывает заметное влияние на климатические процессы. Прежде всего это обусловлено тем, что крупномасштабные атмосферные течения, наряду с океаническими течениями, обеспечивают меридиональный и азимутальный перенос тепла. Помимо тепла, атмосферные потоки переносят угловой момент, что приводит к формированию средних зональных течений, циклонов и антициклонов различного масштаба. Структура и динамика общей циркуляции атмосферы очень сложны и зависят от целого ряда факторов, таких как вращение Земли, солнечное излучение, рельеф поверхности и многое другое. Несмотря на очевидный прогресс в области численного моделирования общей циркуляции атмосферы, прогнозировать важные для формирования погоды явления, например, блокирующие антициклоны, пока не удается. Это связано с тем, что процессы в атмосфере являются сильно нелинейными и до полного понимания сложных взаимодействий между различными элементами системы, состоящей из атмосферы, суши и океана, еще очень далеко. Атмосферная циркуляция имеет конвективную природу, а ее основным

источником служит меридиональный перепад температур — между полюсом и экватором. Меридиональный перепад температур не постоянен, он может варьироваться как в результате сезонных колебаний, так и благодаря другим процессам. Например, арктическое потепление приводит к снижению меридионального перепада температур [1].

Разобраться в сложных нелинейных процессах при наличии обратных связей и целого ряда определяющих факторов чрезвычайно трудно. В этом случае обычно редуцируется количество параметров, описывающих поведение системы, что значительно облегчает задачу. Одним из подходов, позволяющих упростить систему и при этом сохранить качественное подобие, является лабораторное моделирование [2, 3]. Лабораторные модели представляют собой реальные физические системы и дают возможность детально изучить роль отдельных, наиболее важных характеристик. Несомненное достоинство экспериментальных исследований — это контроль выполнения граничных условий, воспроизводимость результатов и осуществимость серий измерений. Классическая лабораторная модель атмосферной циркуляции средних широт (модель Хайда) предложена в [4] и выглядит как вращающийся цилиндрический слой с изотермическими боковыми стенками и свободной верхней границей. Внешняя поверхность стенок горячая, а внутренняя, соответственно, холодная. Таким образом, рассматривается вращающийся цилиндрический слой с горизонтальным перепадом температур. Такая конфигурация подобна теоретической модели Иди [5], что значительно облегчает анализ экспериментальных результатов. Данная модель успешно использовалась в течение десятилетий для изучения самых разных аспектов формирования бароклинных волн в средних широтах [6]. Последние исследования в рамках модели Хайда были направлены на изучение влияния на формирование бароклинных волн рельефа и неоднородного распределения температуры [7, 8].

Локализация областей нагрева и охлаждения по вертикали и горизонтали может оказывать существенное влияние на динамику и структуру течения. Это показано в экспериментах на модели крупномасштабной циркуляции атмосферы, предложенной Фультцем [9]. В модели Фультца рассматривался цилиндрический слой, нагреваемый на периферии дна и охлаждаемый в центре. Реализовано два варианта охлаждения на дне: при помощи спрея или цилиндрической вставки, внутрь которой помещался лед. Течения, формирующиеся в модели Фультца, имели структуру, подобную типичным крупномасштабным атмосферным течениям. Однако они оказались существенно менее устойчивыми и регулярными, чем течения в цилиндрическом зазоре с изотермическими стенками. Сложность и нерегулярная структура течений в модели Фультца при крайне ограниченных средствах анализа экспериментальных данных, свойственных времени ее создания, послужили основной причиной отказа от данной конфигурации и выбора в качестве базовой для моделирования крупномасштабной циркуляции атмосферы более простой модели Хайда.

Надо отметить, что реальная атмосфера характеризуется выраженным эффективным нагревом вблизи поверхности в области тропиков и охлаждением в верхних слоях атмосферы в полярной области. Это послужило мотивацией для создания модели с граничными условиями, более приближенными к реальным условиям в атмосфере [10]. Модель [10] является модификацией модели Хайда, в которой нагрев локализован в кольцевой области на периферии дна, а охлаждение — в центральной области слоя, вблизи его поверхности. Показано, что течение в данной конфигурации демонстрирует более сложную пространственную структуру и динамику, в том числе взаимодействие свободно-конвективных течений и бароклинных волн. Эти особенности не отображались классической моделью Хайда. Использование новой модели для моделирования течений в условиях, приближенных к реальным, показало перспективы ее применимости.

Еще одним важным параметром, определяющим глобальную атмосферную циркуляцию, служит аспектное отношение a (отношение вертикального масштаба к горизонтальному). Для реальных крупномасштабных атмосферных течений отношение характерного вертикального масштаба (порядка двадцати километров) к горизонтальному масштабу (порядка тысячи километров), в отличие от лабораторных моделей, очень мало. Аспектное отношение для экспериментов в рамках модели Хайда обычно больше единицы [6], а в модифицированной модели [10] оно лишь чуть меньше единицы ( a ≈ 0.65) . Зависимость характеристик течения от аспектного отношения проявляется даже в случае простого — осесимметричного — режима, подобного циркуляции Хэдли. Этот режим реализуется при значении термического числа Россби, заметно большем единицы. В таком случае эффекты, связанные с вращением, относительно слабы, и наложенный горизонтальный перепад температур приводит к формированию меридиональной конвективной ячейки, занимающей весь слой жидкости. Cравнение результатов исследований для различных аспектных отношений [11, 12] убедительно показывает, что, несмотря на качественное подобие наблюдаемых течений, зависимости их характеристик от управляющих параметров существенно разнятся. Поэтому есть достаточно серьезные основания предполагать, что отличия между течениями в слоях с большим и малым аспектными отношениями в более сложном — волновом — режиме будут еще более сильными.

Первые результаты, полученные при помощи лабораторной модели общей циркуляции атмосферы с малым аспектным отношением ( a ≈ 0.09 ) представлены в [13], где посредством визуализации течения алюминиевой пудрой показано, что с уменьшением термического числа Россби Ro _T и увеличением числа

Тейлора Ta происходит переход от осесимметричного режима к режиму с бароклинными волнами. Наблюдение за движением трассеров вблизи верхней границы дает лишь ограниченную информацию о структуре течений, поэтому для определения структуры среднего течения в объеме жидкости разработана математическая модель в постановке, максимально приближенной к лабораторной модели. В данной работе представлены первые результаты, полученные при реализации этой математической модели, и выполнено их сравнение с данными эксперимента.

2.    Лабораторное моделирование общей циркуляции атмосферы

Перед тем, как перейти к описанию предлагаемой математической модели и полученным при ее помощи результатам, необходимо дать краткое описание новой лабораторной модели общей циркуляции атмосферы с малым аспектным отношением a , реализованной в [13]. Принципиальная схема модели общей циркуляции атмосферы представлена на

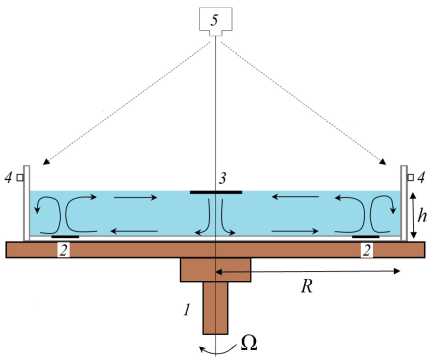
Рис. 1. Схема лабораторной модели общей циркуляции атмосферы: 1 – вращающийся стенд, 2 – кольцевой нагреватель, 3 – дисковый холодильник, 4 – светодиодная лента, 5 – цифровая видеокамера

рисунке 1. Рассматривается вращающийся на стенде (1) слой жидкости с a«0.09 при наличии локализованного   кольцевого   нагревателя   (2), расположенного на периферии дна, и холодильника (3) в форме диска, который находится в центральной части верхней границы слоя жидкости. Кольцевой нагреватель моделирует нагрев на   экваторе, а холодильник — охлаждение в полярной области. Нагреватель специально смещен от боковой стенки для минимизации ее влияния на формирование течений за счет прилипания. Помимо этого, удаление области нагрева от боковой стенки позволяет реализовать в верхней части слоя жидкости, зональные течения (имитировать восточные и западные ветры), характерные для экваториальной области. Благодаря переносу углового момента, радиальное течение, направленное к боковой стенке (Рис. 1) формирует антициклоническую циркуляцию (противоположную вращению модели), а конвергентное течение (направленное к центру) приводит к появлению интенсивного циклонического движения.

Экспериментальная модель представляет собой кювету квадратного сечения со стороной 700 мм и высотой 200 мм. Для реализации цилиндрического слоя в кювету вставлена дополнительная цилиндрическая стенка из оргстекла толщиной 3 мм и радиусом R = 345 мм. Кольцевой электрический нагреватель имеет ширину 25 мм. Расстояние от боковой стенки до внешней границы нагревателя составляет 40 мм. Нагреватель изготовлен из тонкой медной фольги (толщиной ~50 мкм), поэтому температура его поверхности сильно зависит от структуры потока. Во время эксперимента мощность нагрева контролируется и поддерживается постоянной. Оценка температуры нагревателя производится при помощи известного соотношения между числом Нуссельта и числом Релея Nu = c • Ra^³ (коэффициент c обычно принимает значения от 0.1 до 0.2). Постоянную температуру в помещении обеспечивает система кондиционирования воздуха, а охлаждение жидкости достигается за счет теплообмена с окружающим воздухом на свободной поверхности, работы центральной системы охлаждения и потока тепла через боковую стенку. Система охлаждения состоит из массивного (толщиной 10 мм) медного диска диаметром 54 мм, погруженного на 2 мм в слой жидкости. Небольшой размер холодильника обусловлен желанием минимизировать влияние твердой крышки, поскольку трение на твердых границах играет важную роль в балансе углового момента при конвекции во вращающемся слое [14]. Верхняя поверхность медного диска охлаждается термоэлектрическим способом (элементом Пельтье). Для отвода тепла с горячей стороны элемента Пельтье используется радиатор с принудительной циркуляцией воздуха. Для снижения влияния циркуляции воздуха на течения жидкости вблизи верхней свободной границы система охлаждения окружена дополнительным открытым боксом. Температура холодильника измеряется медь-константановой термопарой, установленной в медный диск.

В качестве рабочей жидкости используется полиметилсилоксановая жидкость (силиконовое масло) ПМС-5. Во всех представленных в [13] экспериментах толщина слоя жидкости h составляет 30 мм, поверхность жидкости является открытой. Для оценки средней температуры жидкости проводятся измерения температуры медь-константановой термопарой, расположенной внутри слоя, на высоте 15 мм и радиусе 180 мм. Основные свойства жидкости и параметры экспериментальной установки приведены в таблице 1.

Для визуализации структуры потока в верхнем слое применяется алюминиевая пудра. Подсветка трассеров обеспечивается светодиодной лентой ( 4 ), размещенной по внешнему периметру экспериментальной модели над слоем жидкости (Рис. 1). Алюминиевые частицы, ориентированные вдоль

Таблица 1. Основные параметры лабораторной модели потока, при съемке сверху яркие, когда поток жидкости горизонтальный, и темные, когда преобладают вертикальные движения. Такая Параметр Обозначение Значение Единицы измерения Свойства жидкости зависимость яркости алюминиевых частиц от соотношения горизонтальной и вертикальной компонент скорости позволяет визуализировать трехмерные структуры. Плотность ρ 911 кг/м3 Кинематическая вязкость ν 5.2·10–6 м2/с Температуропроводность χ 8.3·10–8 м2/с Съемка изображений осуществляется с помощью 4-мегапиксельной CCD камеры Bobcat 2020 (5). Большинство изображений Коэффициент объемного расширения β 9·10–4 1/K Число Прандтля Pr =νχ 62.7 записывется с частотой 1 Гц. Характеристики экспериментальной установки В качестве основных безразмерных параметров используются термическое число Россби RoT , число Тейлора Ta и число Экмана E : Радиус слоя жидкости R 345 мм Высота слоя жидкости h 30 мм Ширина нагревателя l 25 мм gβh∆T        4Ω2R5        ν Центральный радиус rh 293 нагревателя мм RoT = Ω2R2, Ta= hν2 , E=Ωh2, Радиус холодильника rc 28 мм где ν — кинематическая вязкость, β — температурный коэффициент объемного расширения, g — ускорение свободного падения, ∆T — перепад температуры между в области нагрева контролируется поток тепла, Мощность нагрева Ph 123 Вт Мощность холодильника Pc ≈ 3 Вт нагревателем и холодильником. Несмотря на то, что а не температура, термическое число Россби выражается через перепад температуры; этот выбор продиктован желанием сравнить полученные результаты с результатами других авторов, которые рассматривают, как правило, изотермические условия в области нагрева и охлаждения. Следует отметить, что в основные управляющие параметры, которые обычно характеризуют режимы течения в системах с бароклинными волнами (термическое число Россби, число Тейлора и число Екмана) не входит температуропроводность. Это можно объяснить тем, что подавляющее большинство таких исследований реализовано на воде, и физические свойства среды считаются более или менее постоянными. Однако немногочисленные работы, в которых используются различные рабочие жидкости, показали, что изменение числа Прандтля оказывает заметное влияние на формирование бароклинных волн [15, 16]. Рост числа Прандтля дестабилизирует волновые течения и приводит к более раннему (при росте скорости вращения) выходу на режим нерегулярных волн.

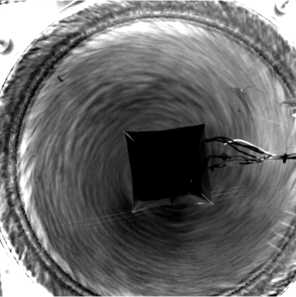
Измерения проводились после установления квазистационарного режима при фиксированных мощностях нагрева и охлаждения для различных скоростей вращения. Структура течений при больших значениях термического числа Россби, когда доминируют свободно-конвективные течения, представлена на рисунке 2. Кольцевая область, видимая на периферии (Рис. 2 a ), является нагревателем, который обеспечивает интенсивное конвективное течение, состоящее из большого количества мелкомасштабных всплывающих тепловых плюмов. В соответствии со схемой лабораторной модели, представленной на рисунке 1, восходящий конвективный поток над нагревателем способствует формированию конвергентных и дивергентных радиальных потоков в верхнем слое. Радиальный перенос углового момента вызывает антициклоническую циркуляцию (восточные ветры) вблизи боковой стенки и циклоническую циркуляцию (западные ветры) на радиусах, меньших, чем радиус нагревателя (Рис. 2 б ). Наблюдаемая циклоническая часть течения почти осесимметрична и аналогична режиму Хэдли [9, 10, 12].

а

Рис. 2. Структура течения в осесимметричном режиме при Ro _T = 14 , Ta = 1.7 ⋅ 10⁸ , E = 0.068 : визуализация алюминиевой

пудрой (осредненное изображение) ( а ); среднее векторное поле скорости ( б )

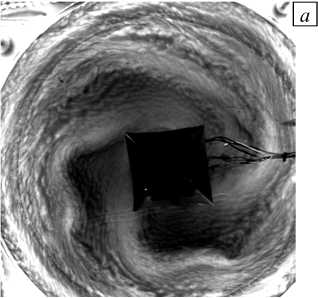
Увеличение числа Тейлора и уменьшение термического числа Россби приводит к неустойчивости осесимметричного течения и появлению бароклинных волн, что хорошо согласуется с результатами других авторов [6, 9, 10]. Мгновенные изображения (см. Рис. 3) показывают, что присутствуют характерные течения в режиме с бароклинными волнами. Необходимо отметить, что существует важное различие между структурой и динамикой потока в классической кольцевой конфигурации [6], предложенной в [10], и постановке, рассматриваемой здесь (Рис. 1). В классической конфигурации на карте Ro _T –t a существует область, где формируются устойчивые регулярные волны. Переход от вертикальных изотермических границ к локализованному горизонтальному нагреву и охлаждению [10] уменьшает область устойчивых волн. В экспериментах [13] в режимах с явными бароклинными волнами (см. Рис. 3) поток постоянно эволюционирует, что приводит к изменению амплитуды и формы волн.

а

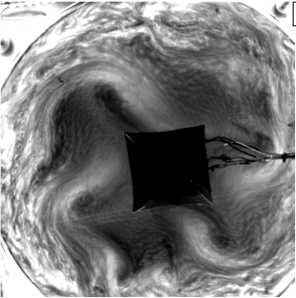
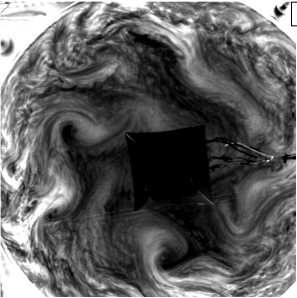
Рис. 3. Структура течения, визуализированная алюминиевой пудрой, в режиме с бароклинными волнами при разных значениях основных безразмерных параметров:  Ro T = 1.6, Ta = 1.4 - 10 9 , E = 0.024  ( а );  Ro _T = 0.7,  Ta = 3.6 - 10 9 ,  E = 0.015  ( б) ;

Ro _T = 0.4, Ta = 6 - 10 9 , E = 0.012 ( в )

3.    Математическое моделирование

Основная цель данной работы — воссоздание в математической модели трехмерной структуры течений в постановке, максимально приближенной к экспериментам [13]. Для решения этой задачи выполнено прямое численное моделирование тепловой конвекции во вращающемся цилиндрическом слое с помощью свободно распространяемого пакета вычислительной гидродинамики OpenFOAM v2106. Расчетная область (см. Рис. 4) по своим геометрическим размерам, расположению кольцевого нагревателя и холодильника является копией экспериментальной модели.

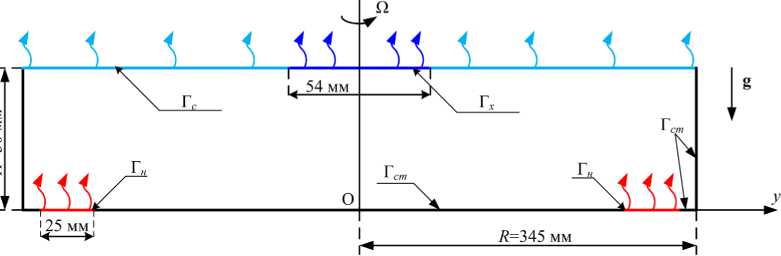
Рис. 4. Схема расчетной области

Система уравнений, описывающая движение несжимаемой жидкой среды с постоянными свойствами в приближении Буссинеска имеет вид:

• V- u = 0,

— + ( u -V ) u + 2 0 x u = -v| p- 1 + vV ² u + p ( T - T_o ) g e z ,                     (1)

• dt                            (Po J

dT+(u-V) T = ZV2 T,

где t — время, u = (ux, uy, uz) — скорость, V — оператор набла, T — температура, p — давление, v — кинематическая вязкость, в — температурный коэффициент объемного расширения, р0 и To — средние по объему начальная плотность и температура рабочей жидкости, g — ускорение свободного падения, Ω — скорость вращения системы вокруг центральной оси, направленной против силы тяжести Ω= Ωez , ez — вертикальный единичный вектор, направленный против силы тяжести. Система уравнений (1) решается с помощью модифицированного решателя buoyantBoussinisqPimpleFoam, в который для учета влияния вращения на тепловую конвекцию добавляется сила Кориолиса f = -2ρ0 Ω×u.

Расчетная область покрывалась многоблочной структурированной сеткой с общим числом контрольных объемов 2,8 млн. Вблизи нижней и верхней границ для разрешения динамических и тепловых пограничных слоев сетка дополнительно сгущается. Интегрирование по времени выполняется согласно неявной схеме Эйлера второго порядка точности. Шаг интегрирования является адаптивным, критерий Куранта–Фридрихса–Леви не превышает 0.4. Для дискретизации конвективных и диффузионных слагаемых используется центрально-разностная схема второго порядка аппроксимации (в OpenFoam эта схема называется Gauss linear). Для решения системы линейных алгебраических уравнений, полученных после дискретизации, применяется метод бисопряженных градиентов PBiCG с предобуславливателем DILU (для скорости и температуры) и GAMG метод (для давления).

Задача решается при следующих граничных условиях:

• –    на боковых стенках Γ ст и части нижней границы, а также на нагревателе Γ _н и холодильнике Γ _х имеет место прилипание жидкости

^u I = u = u = 0; ст          х          н

• –    на свободной верхней границе Γ _c выполняется условие проскальзывания

  u_z

  
  

  Γ c

  
  

  ∂ u x

  
  

  ∂ z

  
  

  ∂ u_y

  
  

  ∂ z

  
  

  Γ c

  
  

  = 0;

  
  

  – боковые стенки и часть дна кюветы являются адиабатическими

∂ T ∂ n

г cm

= 0;

– на нагревателе, холодильнике и свободной верхней границе известен тепловой поток

∂T P н ∂T =P х ∂T P-P нс ∂z Γн λSн, ∂z Γх λSх, ∂z Γс λSс где Pн — мощность нагревателя, Pх — мощность холодильника, Sн — площадь нагревателя, Sх — площадь холодильника, Sс — площадь свободной верхней границы, λ — теплопроводность.

4.    Структура среднего течения

Математическое моделирование, в отличие от эксперимента, позволяет получить мгновенные трехмерные распределения всех интересующих характеристик течения. Но при этом очевидный выигрыш в объеме информации получается за счет колоссального роста временных затрат: так, для моделирования 1 с физического времени на 112 ядрах вычислительного кластера Тритон требуется примерно 300 с расчетного времени. Это ограничивает количество серий и длительность расчетов, проводимых при помощи математической модели (вычислительного двойника) лабораторной модели общей циркуляции атмосферы. Значения основных параметров для четырех расчетных серий представлены в таблице 2. Расчеты 1-й и 2-й соответствуют осесимметричному режиму, а 3-й и 4-й — режиму с бароклинными волнами.

Структура среднего течения в осесимметричном режиме показана на рисунках 5, 6. Осреднение по времени проведено на основе 200 мгновенных трехмерных распределений. Это соответствует интервалу физического времени

Таблица 2. Значения основных параметров в 2000 с (данные расчетов сохранялись с частотой 0.1 Гц). Для осреднения по азимутальной координате использовано 130 вертикальных сечений (с шагом по углу чуть меньше 3 градусов). Средняя № расчета Ω, рад/c Pн, Вт Pх, Вт ∆T , К RoT Ta E 1-й 0.08 30 2 13.3 4.4 1.7·108 0.068 2-й 0.08 112 3 26.1 8.7 1.7·108 0.068 меридиональная циркуляция отвечает 3-й 0.37 30 2 14.9 0.2 3.6·109 0.015 схеме течений, на основе которой реализована лабораторная модель. В области нагрева и охлаждения 4-й 0.37 112 3 25.1 0.4 3.6·109 0.015 формируются интенсивные подъемное и опускное течения, которые приводят к образованию двух меридиональных ячеек (Рис. 5). Основная меридиональная ячейка, аналог циркуляции Хэдли, занимает большую часть слоя, от оси до нагревателя. Соседняя с ней ячейка с циркуляцией противоположного направления находится на периферии, между нагревателем и боковой стенкой (см. Рис. 1). Основным отличием представленных течений от полученных в работе [12], в которой нагреватель находится прямо у боковой стенки, является наличие интенсивного антициклонического (отстающего от вращения модели) течения в верхней части слоя на периферии (Рис. 6а, б). В области основной меридиональной ячейки явно доминирует циклоническое движение, за исключением малой области в нижней части слоя, вблизи нагревателя, где формируется слабое антициклоническое течение. Существенное изменение мощности нагрева и связанное с ним увеличение термического числа Россби при фиксированной скорости вращения не приводит к качественным изменениям структуры азимутального и меридионального течений. С увеличением скорости вращения и соответствующим изменением значений термического числа Россби и Тейлора в рассматриваемой системе происходит переход от осесимметричного режима (Рис. 7а) к волновому режиму (Рис. 7б), что хорошо согласуется с результатами экспериментов (Рис. 2а, б и Рис. 3б). Видеоролики, демонстрирующие изменение структуры течения с ростом числа Тейлора представлены в [17].

Рис. 5. Линии тока и модуль скорости средней (по времени и азимутальной координате) меридиональной циркуляции в осесимметричном режиме; расчеты 1-й ( а ) и 2-й ( б ) (см. Табл. 2)

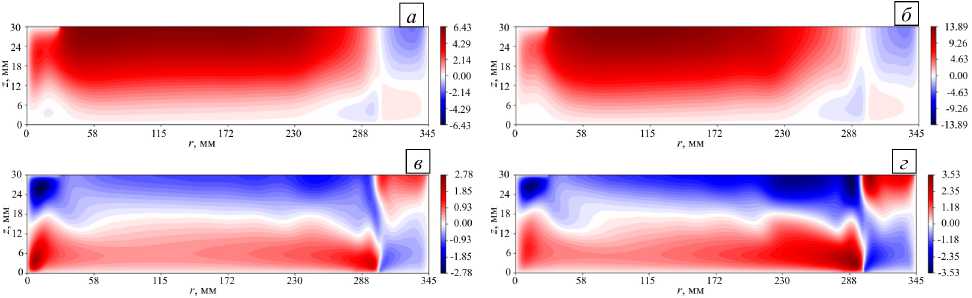
Рис. 6. Средние (по времени и азимутальной координате) распределения азимутальной ( а , б ) и радиальной скорости ( в , г ) в осесимметричном режиме; расчеты 1-й ( а , в ) и 2-й ( б , г )

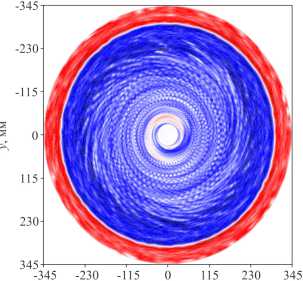
-1.75

-3.49

-5.24

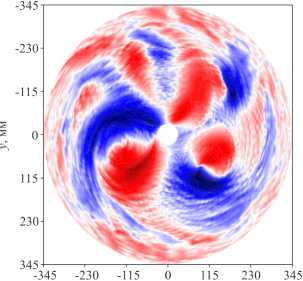
Рис. 7. Мгновенные распределения радиальной скорости на верхней границе слоя: расчеты 2-й ( а ) и 4-й ( б )

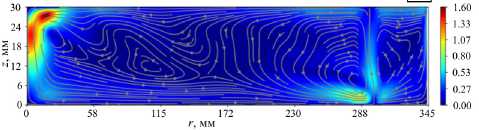
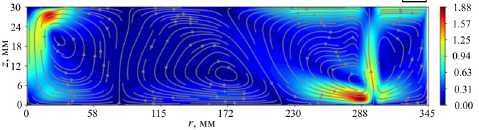
Рис. 8. Линии тока и модуль скорости средней (по времени и азимутальной координате) меридиональной циркуляции в режиме с бароклиннымы волнами; расчеты 3-й ( а ) и 4-й ( б )

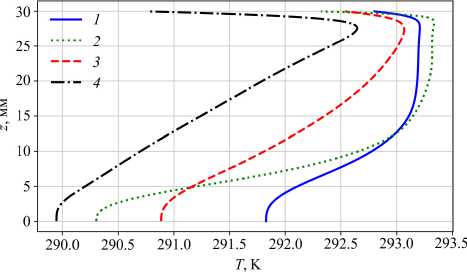
Рис. 9. Средние (по времени и азимутальной координате) вертикальные профили температуры на среднем радиусе ( R = 172мм)

В волновом режиме, в отличие от осесимметричного режима, увеличение мощности нагрева приводит к качественному изменению структуры среднего течения (Рис. 8). При меньшей мощности нагрева (расчет 3-й) средняя меридиональная циркуляция состоит из трех ячеек: периферийной, ограниченной боковой стенкой, средней (аналога ячейки Хэдли) и центральной (аналога полярной ячейки), причем граница между центральной и средней ячейками очень сильно размыта (Рис. 8а). При увеличении нагрева (расчет 4-й) хорошо различимы четыре меридиональные ячейки. Кроме пристеночной и аналогов ячеек Хэдли и полярной, появляется аналог ячейки Ферреля. Эта ячейка, как и в земной атмосфере, менее интенсивная, чем полярная ячейка и ячейка Хэдли (Рис. 8б). Особенность ячейки Ферреля (и ее экспериментального аналога) заключается в том, что она формируется вследствие волновых движений и заметна только на средних (по времени и азимутальной координате) распределениях меридиональной циркуляции. Важно, что область бароклинных волн характеризуется устойчивой стратификацией (Рис. 9).

Столь же сильные изменения с ростом мощности нагрева видны и на средних распределениях азимутальной и радиальной компонент скорости (см. Рис. 10). Азимутальное движение при большом нагреве (Рис. 10б) состоит из трех зональных течений: антициклонического на периферии, циклонического в средней части слоя, циклонического вихря в центральной части. Подобное распределение азимутальных течений также характерно для атмосферы Земли. Меридиональное движение на границе между аналогами ячеек Хэдли и ячейки Ферреля имеет выраженный наклон (в англоязычной литературе такая конвекция имеет специальное название “slantwise convection”).

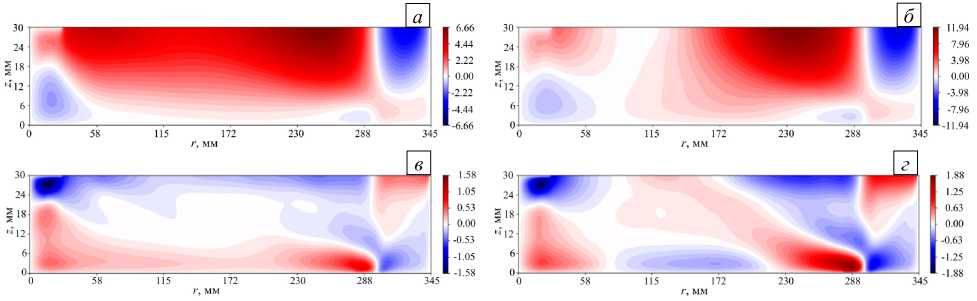
Рис. 10. Средние (по времени и азимутальной координате) распределения азимутальной ( а , б ) и радиальной ( в , г ) компонент скорости в режиме с бароклиннымы волнами; расчеты 3-й ( а , в ) и 4-й ( б , г )

В рассматриваемой системе, в отличие от классической модели Хайда, бароклинные волны неустойчивы. Как показали эксперименты [13], наблюдаемые бароклинные волны являются суперпозицией различных волновых мод, которые дрейфуют во вращающейся системе в циклоническом направлении. Амплитуда этих волновых мод существенно варьируется с течением времени, причем без выделенной частоты. В связи с этим, помимо средних распределений, полезно проанализировать распределения пульсаций, которые в основном обусловлены волновыми движениями. Действительно, поля пульсаций азимутальной и радиальной компонент скорости в осесимметричном и волновом режимах качественно различны. В осесимметричном режиме (Рис. 11) пульсации скорости сосредоточены над нагревателем и под холодильником, в областях подъемного и опускного течений, образованных мелкомасштабными конвективными структурами. В волновом режиме пульсации локализованы в верхней части слоя, в области формирования бароклинных волн (Рис. 12). С ростом нагрева интенсивность пульсаций увеличивается в несколько раз.

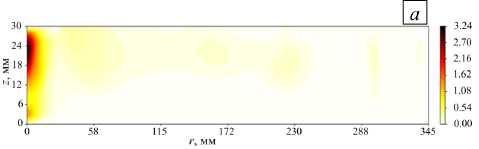
Рис. 11. Поле пульсаций азимутальной ( а ) и радиальной ( б ) компонент скорости; расчет 2-й

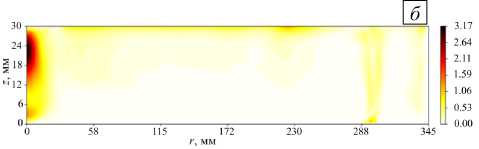
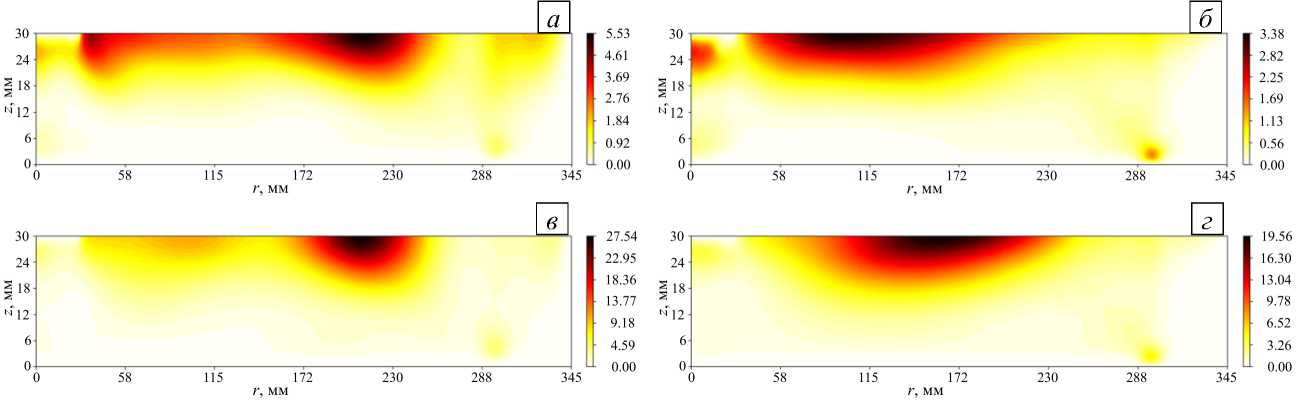
Рис. 12. Поле пульсаций азимутальной ( а , в ) и радиальной ( б , г ) компонент скорости; расчеты 3-й ( а , б ) и 4-й ( в , г )

5.    Заключение

Представлены первые результаты математического моделирования в постановке, приближенной к новой лабораторной модели общей циркуляции атмосферы [13]. Получено хорошее качественное согласование экспериментальных и численных результатов. Эксперименты [13] ограничены визуализацией течений на верхней свободной границе, что не дает возможности выявить структуру течений в объеме жидкости. Основной целью проведенных расчетов было определение средней структуры течения в осесимметричном и волновом режимах. Показано, что в осесимметричном режиме реализуется меридиональная циркуляция, аналогичная циркуляции Хэдли, со сравнительно низким уровнем пульсаций скорости. Обнаружено, что увеличение скорости вращения приводит к формированию неустойчивых бароклинных волн и существенному изменению структуры меридиональной циркуляции. Интенсивность и структура бароклинных волновых движений в значительной степени обуславливается интенсивностью нагрева. Впервые продемонстрировано, что в лабораторной модели при относительно малом значении термического числа Россби возможна реализация меридиональной циркуляции со структурой, подобной наблюдаемой в атмосфере, состоящей из аналогов ячейки Хэдли, ячейки Ферреля и полярной ячейки. Это подтверждает перспективность использования новой лабораторной модели общей циркуляции атмосферы для выявления ключевых факторов, определяющих структуру и динамику крупномасштабных атмосферных течений.

Вычислительные ресурсы на кластере «Тритон» ИМСС УрО РАН обеспечены в рамках темы АААА-А19-119012290101-5.

Исследование выполнено за счет гранта Российского научного фонда (проект № 22-21-00572) .