Структурная многоэлементная модель вязкоупругого материала: концепция и экспериментальная проверка

В сооружениях промышленных предприятий широко используются конструкции, на которые при протекании технологического процесса комплексно воздействуют механические нагрузки, повышенные температуры и агрессивные воздействия. Примерами являются емкости, аппараты, дымовые и вентиляционные трубы, газоходы, газоочистные сооружения, нефтепроводы.

Одним из распространенных типов коррозионностойких конструкций являются конструкции из полимерных композитов, в том числе бипластмассовые с несущим слоем из стеклопластика и коррозионностойким внутренним слоем из химически стойкого термопласта (например, винипласта – непластифицированного поливинилхлорида, фторопласта (тефлона), полиэтилена и др.). Такие конструкции в большинстве своем применяются в коррозионностойких трубопроводах [1,2], в том числе для подачи горячей воды [3], транспортировки нефтепродуктов [4], в различных емкостях, травильных ваннах, вентиляционных трубах и газоходах [5], сточных трубопроводах [6] и др.

Вместе с тем существуют и проблемы, связанные с плохой совместимостью стеклпластиковых и термопластовых слоев по тепловым деформациям из-за существенной разницы по деформационным характеристикам и термическому расширению. Чаще всего это приводит к повреждениям химически стойкого термопластового слоя, в котором после длительной эксплуатации возникает сетка трещин и теряется его герметичность [7]. Возникновение такого рода повреждений может быть связано с накоплением остаточных напряжений, формирование которых обусловлено термомеханическим воздействием в стесненных условиях.

Основные причины и механизмы формирования остаточных температурных напряжений в полимерах и композитах обобщены в монографиях [8]–[11], обзорных и исследовательских публикациях. К ним относятся температурные градиенты по толщине конструкций, разное (в том числе анизотропное) температурное расширение компонентов полимерных композитов, особенности технологических режимов отверждения, химическая усадка полимерной матрицы, взаимодействие с технологическим оборудованием и др.

Задачи по прогнозированию остаточных напряжений могут решаться в разных постановках, например, в работе 1976 года [12] задача определения термических и влажностных остаточных напряжений в слоистом полимерном композите решалась в упругой постановке без учета вязкоупругих свойств материалов. При этом большинство других работ по прогнозированию остаточных напряжений в полимерах и композитах обязательно рассматривают вязкоупругие свойства как минимум полимерной матрицы.

Работа 1978 года [13] посвящена исследованию формирующимся на истории термомеханических воздействий остаточным термическим напряжениям в однородных (неармированных и ненаполненных) аморфных полимерах. Здесь описаны принципы формирования замороженных деформаций и напряжений, для их прогнозирования применяются подходы теории упругости и вязкоупругости, учитываются эффекты ориентации макромолекул.

В работе 1996 года [14] предложена процедура для расчета остаточных термических напряжений при a step-by-step cooling cycle неизотермическом охлаждении в композитных изделиях с полимерной матрицей с учетом ее вязкоупругих свойств.

До настоящего времени рассматриваемая тема не потеряла актуальности, об этом говорит большое количество современных работ.

Например, в работе 2005 года [15] для определения напряжений (в том числе остаточных) в стеклоподобном материале применяют метод конечных элементов с использованием известной вязкоупругой модели Максвелла [16].

В работе 2016 года [17] решается задача вычисления, возникающих в процессе отверждения, остаточных напряжений в композитах с полимерной матрицей. Для различных состояний материала на разных стадиях задача решается в упругой или вязкоупругой постановке.

В работах 2016, 2018 годов [18,19] показан подход с использованием многомасштабного моделирования методом конечных элементов для описания вязкоупругопластического поведения однонаправленных композитов с полимерной матрицей и прогнозирования формирования остаточных термических напряжений в процессе отверждения.

Причины формирования остаточных напряжений в термопластичных полимерах рассмотрены в работе [20], методы их измерения приведены в работе [21], один из способов численного моделирования остаточных напряжений в сварных соединениях термопластовых конструкций рассмотрен в [22].

В обзорной работе [23] показано актуальное состояние в области структурных моделей полимерных материалов, позволяющих моделировать вязкоупругие процессы (ползучесть, релаксацию), переход через температуру стеклования. В данной работе приведено описание 19 структурных вязкоупругих моделей каждая из которых имеет свои особенности.

Перечисленные выше работы в основном относятся к областям машиностроения, автомобилестроения, авиастроения и даже медицины, при этом работ, посвященных строительным конструкциям из полимерных композитов относительно немного, а вопросам накопления в них температурных напряжений в процессе длительной эксплуатации при переменных температурах – еще меньше. Работа строительных конструкций из полимерных композитов будет иметь свои особенности, на которые необходимо ориентироваться.

Температурно-временная зависимость механических свойств пластмасс обусловливает специфическое изменение напряженного состояния элемента со стесненной деформацией при теплосменах, обнаруживаемое экспериментально [7,13] и проявляющееся в накоплении остаточных напряжений, внешним проявлением которых, например, может являться сетка трещин Mishnev, M.; Zadorin, A.; Korolev, A; Alabugina D.; Pyankova, A.; Shamberger, A.; Astashkin, V.

Structural multi-element model of viscoelastic material: Concept and experimental testing;

в полимерной матрице. Причиной появления внутренних напряжений являются нереализованные тепловые деформации, а их эволюция и накопление обусловлены протеканием взаимосвязанных процессов ползучести и релаксации, скорость которых меняется с изменением температуры и уровня нагруженности. Одним из следствий является то, что остаточные напряжения в конструкции могут зарождаться не только в процессе изготовления и затем эволюционировать на протяжении всего срока эксплуатации. Например, они могут накапливаться в отдельных элементах конструкций из полимерных композитов при многократном повторении циклов нагрева и охлаждения.

Для прогнозирования вязкоупругого поведения полимеров и композитов при циклическом термомеханическом воздействии нами предлагается подход с использованием структурной многоэлементной модели, включающей в себя несколько моделей Кельвина – Фойгта [24]–[26], которая была предложена и описана в работах [7], [27], [28].

Экспериментальная проверка данной модели проводилась в небольшом объеме на примере бипластмассовой конструкции с внутренним слоем из термопластичного полимера – непластифицированного поливинилхлорида [29]. В данной работе уровень температурных напряжений оценивался косвенно по приобретенной в результате термомеханического воздействия кривизне бипласмассовых плоских образцов. В такой постановке достаточно сложно достоверно определить уровень температурных напряжений в каждом отдельном слое конструкции и оценить их возможное накопление, поскольку на результат оказывают взаимное влияние механические вязкоупругие свойства стеклопластика и термопласта, податливость контактного (клеевого) слоя, условия закрепления образцов и т.д. Поэтому существует необходимость разработки прямой методики экспериментальной оценки и теоретического прогнозирования возникновения и эволюции остаточных напряжений при термомеханическом воздействии в процессе эксплуатации в вышеописанных конструкциях.

При прогнозировании возникновения остаточных напряжений в полимерных материалах нельзя обойти без учета их реологических свойств. Большинство исследований конструктивных реологических свойств полимеров и композитов относится к стационарному режиму эксплуатации, при этом распространенные феноменологические подходы трудно применять для нестационарных процессов. Наиболее широко применяемые для моделирования деформационных свойств пластмасс феноменологические подходы используют наследственные теории [16,26], отражающие главное свойство – вязкоупругость, т.е. возвращение в начальное недеформированное состояние после разгрузки с последующей длительной выдержкой. Однако классические подходы не позволяют учесть память на температурные воздействия и учесть возможное накопление остаточных напряжений.

Целью настоящей работы является развитие экспериментально-теоретического метода расчетного определения и прогнозирования напряжений при циклическом термомеханическом воздействии, который позволит учитывать память материала при термомеханическом воздействии и возможное накопление остаточных напряжений в полимерных материалах в процессе длительной эксплуатации. Также при успешном развитии предлагаемого подхода, можно предположить, что он окажется эффективным для прогнозирования напряженно-деформированного состояния полимеров и композитов с памятью формы. На текущем этапе в качестве объекта исследований был принят непластифицированный поливинилхлорид (винипласт), широко применяемый в бипластмассовых конструкциях. В дальнейшем планируется развитие и распространение подхода на другие материалы (в том числе реактопласты и армированные композиты).

Основными задачами настоящей работы являлись:

• -    определение механических парметров исследуемого термопласта для вязкоупругой структурной модели Кельвина – Фойгта;

• -    разработка методики и проведение экспериментальных исследований напряженного состояния исследуемого термопласта при совместном действии статической механической нагрузки и циклически меняющейся температуры;

• -    реализация алгоритма расчета с применением предлагаемого подхода и сопоставление с экспериментом результатов моделирования напряженного состояния образца.

• 2    Materials and Methods

  Объектом экспериментальных исследований являлись стержневые образцы из непластифицированного поливинилхлорида (винипласта) по Российскому государственному стандарту ГОСТ 9639 [30]. Размер образцов – 220 х 19 х 5.3 мм.

В ходе работы при экспериментальных исследованиях проводились основные испытания на растяжение в сочетании с циклическим нагревом и охлаждением. Целью данных испытаний было исследование изменения напряженного состояния образца со временем в результате термомеханического воздействия, ползучести и релаксации. Помимо основных испытаний для последующего моделирования предварительно необходимо было провести экспериментальное определение вязкоупругих механических параметров испытываемых образцов.

Испытания на растяжение в сочетании с термомеханическим воздействием, а также определение вязкоупругих характеристик выполнялись на разрывной машине Tinius Olsen h100ku (Horsham, USA) в специально разработанной и изготовленной термокамере. Согласно данным производителя машины Tinius Olsen h100ku, точность измерения нагрузки составляет ±0,5% в диапазоне 0.2–100%. Разрешающая способность измерения перемещения траверсы составляет 0.1 мм с погрешностью до 0.01 мм.

Схема и фото изготовленной термокамеры показаны на рисунке ( Рис. 1, Fig. 1 ). На схеме показан стержневой образец 1, защемленный во внутренних зажимах 4. Термокамера состоит из верхней подвижной части 2 и нижней неподвижной части 3, жестко закрепленной болтами к неподвижному основанию 8 испытательной машины Tinius. Верхняя часть 2 термокамеры находится в подвешенном состоянии, она зажата в верхнем захвате испытательной машины Tinius при помощи шарнирной штанги 10. Верхняя 2 и нижняя 3 части не соприкасаются, что позволяет свободно деформировать защемленный во внутренних захватах 4 образец 1. На образец 1 устанавливаются обжимные уголковые упоры 7, на которые устанавливаются ножки индикаторов перемещений, что позволит по аналогии с экстензометрами измерять деформации образца на фиксированной длине (базе) и исключить влияние проскальзывания образца в захватах.

Изготовленная термокамера позволяет с хорошей точностью проводить испытания на растяжение и сжатие при повышенных температурах. Точность измерения нагрузки на образец обеспечивается достаточной чувствительностью испытательной машины Tinius, поскольку (в отличие, например, от промышленных приборов для ДМА анализа) установка предназначена для испытаний относительно крупноразмерных образцов, что требует меньшей чувствительности сенсоров оборудования, т.к. испытания проводятся при относительно больших нагрузках и больше подходит для исследования строительных конструкций, имеющих большие габариты.

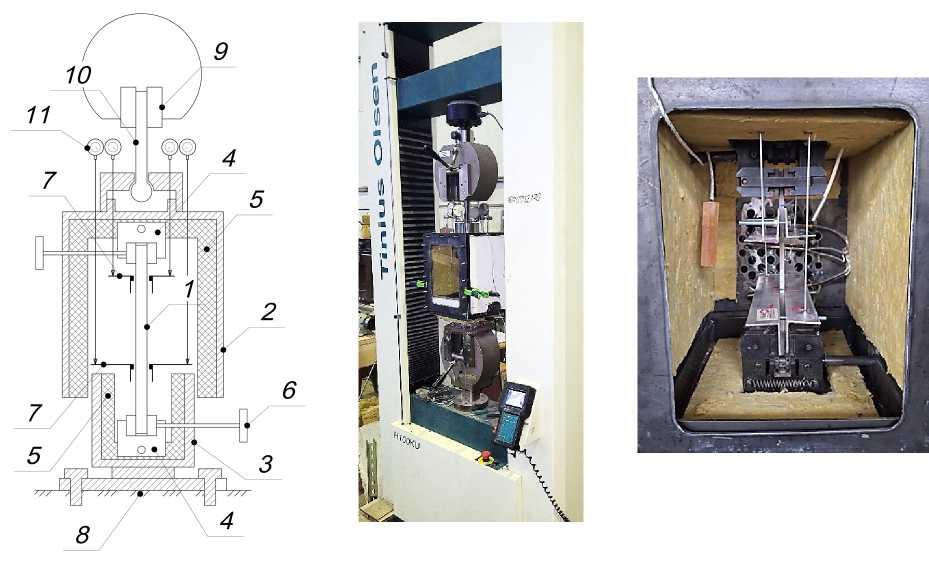
Рис. 1 – Схема термокамеры, фото экспериментального стенда и установленного в него образца.

• Fig. 1 – Scheme of the thermal chamber, photo of the experimental stand and the sample installed in it.

Эксперимент на циклическое термомеханическое воздействие состоял из следующих этапов:

• 1.    Стержневой образец из винипласта с предварительно установленными на нем уголковыми обжимными упорами зажимался во внутренних захватах установки. Термокамера и установленный в нее образец прогревались до постоянной температуры 30°С.

• 2.    К образцу прикладывалась начальная растягивающая нагрузка 1800 Н, при этом по индикаторам фиксировались перемещения в пределах базы для контрольного определения мгновенного модуля упругости E 1 . Скорость перемещения захвата испытательной машины 5 мм/мин. После достижения нагрузки захваты оставались в одном положении, и деформация образца от механической нагрузки не менялась, при этом нагрузка релаксировала.

• 3.    В момент достижения нагрузки 1800 Н включался режим нагрева образца. Образец нагревается до 75°С за 6 мин 20 с (средняя скорость нагрева составляет 0.118 °С / с). При нагреве образец расширялся и, поскольку он жестко зафиксирован в захватах, в нем нарастали температурные напряжения сжатия, которые накладываясь на растягивающие механические напряжения, снижали их, что отражалось на кривой зависимости напряжений от времени.

• 4.    В момент достижения температурой на контрольной термопаре значения 75°С включается режим охлаждения образца. Образец охлаждается с 75°С до 30°С за 12 мин 40 с (скорость охлаждения составляет 0.059°С / с). При нагреве образец начинает сжиматься и в нем снижаются температурные напряжения сжатия, которые образовались при нагреве.

• 2.2 Methodology of theoretical research

Циклы нагрева и охлаждения образца повторяются необходимое количество раз, при этом фиксируются значения нагрузок на силоизмерителе испытательной машины, соответствующие пиковым значениям температуры.

Схема испытаний, в которой образец предварительно растягивается механической нагрузкой была принята во-первых, чтобы при нагреве образец находился в напряженном состоянии, что позволяет избежать наложения погрешностей от люфтов в испытательном оборудовании, во-вторых было интересно оценить точность предлагаемой методики при данном сложном виде напряженного состояния, когда релаксирующие растягивающие напряжения комбинируются с меняющими знак и также релаксирующими температурными напряжениями.

Предлагаемая структурная модель полимерного материала является многоэлементной, она состоит из некоторого числа параллельно соединенных элементарных ячеек, каждая из которых представляет собой описанную выше модель Кельвина – Фойгта с одинаковыми для всех ячеек упругими и вязкими элементами. Основной особенностью, отличающей ее от других известных нам моделей, является то, что каждая ячейка снабжена температурным тормозом, который срабатывает при определенной температуре и включает или выключает ячейку из работы. Ячейки выключаются при повышении температуры и включаются при снижении, при этом после выключения ячейка, находящаяся в напряженно-деформированном состоянии, не исчезает, а продолжает работать по закону обратной ползучести. Это позволяет моделировать эффект «памяти».

Изменение с температурой упругих и реологических свойств описывается только изменением числа работающих ячеек, обладающих одинаковыми механическими параметрами. Таким образом, получается линейная зависимость механических свойств от температуры, однако нелинейность может быть учтена если включать ячейки не по одной, а по несколько штук в соответствие с зависимостью механической характеристики от температуры. При этом количество ячеек должно быть достаточно большим.

При тепловом воздействии модель работает следующим образом. Нереализованная в шаге приращения температуры деформация ε0 создает в элементарной ячейке напряжения σ, которые впоследствии релаксируют во времени τ по закону [16,26]:

(- а(т) = H • s + (a0 - H • s0) • e m

После отключения ячейки в момент времени τ *, т.е. после срабатывания тормоза, напряжения в ней становятся равными нулю, и происходит перераспределение напряжений на Mishnev, M.; Zadorin, A.; Korolev, A; Alabugina D.; Pyankova, A.; Shamberger, A.; Astashkin, V.

Structural multi-element model of viscoelastic material: Concept and experimental testing;

работающие ячейки, а деформации в ячейках изменяются по закону обратной ползучести (можно назвать такую деформацию виртуальной):

S v ^T ) = ( s ₀

£ 1). e' E r m ’ E

где E 1 – мгновенный модуль упругости, E 2 – упругий параметр материала, η – коэффициент вязкости, H=E 1 E 2 /(E 1 +E 2 ) – длительный модуль упругости, m=η/(E 1 +E 2 ) – время релаксации.

При снижении температуры до определенного значения выключенные ячейки включаются обратно, при этом виртуальные деформации, которые нарастали в выключенном состоянии, переходят в напряжения суммируются с механическими и температурными напряжениями, равномерно распределенными между включенными ячейками. При этом в каждой включаемой ячейке напряжения от замороженных деформаций будут отличаться, поскольку их включение и выключение происходит при разных температурах в разные моменты времени. Накопленные напряжения, вызванные виртуальными деформациями, и будут являться остаточными напряжениями, сформированными в результате циклического термомеханического воздействия.

Таким образом, если после достижения некоторой повышенной температуры осуществляется охлаждение стержня, то постепенно «замораживаются» вынужденноэластические деформации, возникшие при нагреве стержня. При повторном нагреве «замороженные» вынужденно-эластические деформации по мере повышения температуры постепенно размораживаются, как бы частично компенсируя тепловые деформации стержня. Кривая напряжений при этом не совпадает с кривой напряжений первичного нагрева. По мере приближения рабочей температуры нагрева стержня к температуре стеклования полимера сжимающие напряжения при нагреве снижаются после достижения некоторого максимума, а уровень остаточных растягивающих напряжений после охлаждения увеличивается.

Последовательность основных этапов работы модели в рамках проводимого эксперимента схематически показана на рисунке ( Рис. 2, Fig. 2 ).

Initial stage

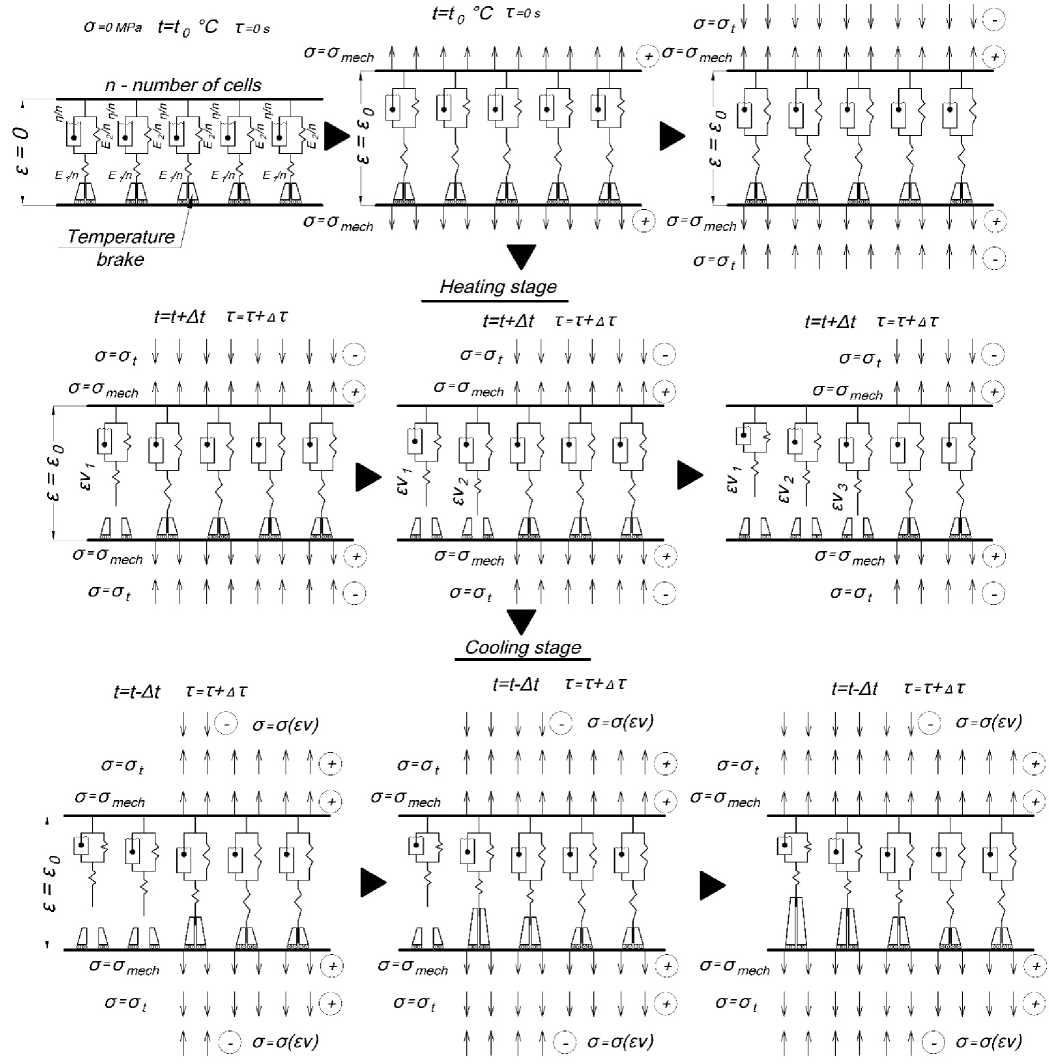
Рис. 2 – Принципиальная схема работы предлагаемой структурной модели в рамках проводимого эксперимента на циклическое термомеханическое воздействие.

Fig. 2 – The principal scheme of the proposed structural model operation under the conducted experiment on cyclic thermomechanical loading.

Описанный выше теоретический подход и предлагаемая структурная модель базируются на использовании трехэлементной вязкоупругой структурной модели материала ( Рис. 3, Fig. 3 ), известной в литературе как модель Кельвина – Фойгта [25,26,31].

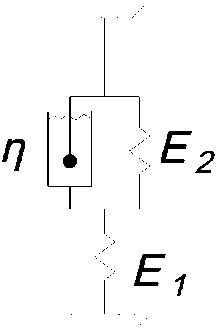
Рис. 3 – Схема вязкоупругой модели Кельвина – Фойгта (E 1 , E 2 – упругие параметры, η – коэффициент вязкости).

Fig. 3 – Scheme of the Kelvin-Voigt viscoelastic model (E1, E2 - elastic parameters, η - viscosity coefficient).

Закон деформирования, описываемый данной моделью, выглядит следующим образом:

E • n • s + H • £ = n • a + a здесь E=E-i, H = E1 E2, n = —n—. Коэффициент E представляет собой мгновенный модуль Е1+Е2     Е1+Е2

упругости, H – длительный модуль упругости, n – время релаксации.

Для определения параметров модели Кельвина – Фойгта проводились испытания образцов на растяжение при постоянной температуре 30°С. Испытания проводились следующим образом: к образцу, помещенному в термокамеру и прогретому постоянной температуры, прикладывалась постоянная растягивающая нагрузка после чего происходило ее снижение в результате релаксации напряжений в образце. По индикаторам фиксировались перемещения образца в пределах базы в момент нагружения для определения параметра E 1 (мгновенный модуль упругости).

Для определения механических параметров использовалось уравнение (1). Задача решалась в академической версии пакета MathCAD и пакете Excel. Для этого согласно экспериментальной кривой релаксации в MathCAD вносились массивы значений напряжений и времени, которому эти напряжения соответствуют. Задавались в первом приближении значения искомых параметров E 2 , η (E1 нам известен), численным методом решалась система экспоненциальных уравнений и подбирались значения E 2 , η. Следует отметить, что поскольку решение выполняется численным методом, то не всегда полученные значения параметров E 2 , η вместе с задаваемым E 1 описывают кривую близкую к экспериментальной. Поэтому полученные предварительные значения переносились в пакет Excel, где путем варьирования добивались наилучшего визуального совпадения экспериментальной кривой с кривой, получаемой из уравнения (1). Параметры, которые обеспечили наилучшее визуальное совпадение кривых, принимались в качестве параметров вязкоупругого деформирования исследуемого материала и в дальнейшем использовались при моделировании.

• 3 Results and Discussion

Для определения вязкоупругих параметров были получены кривые релаксации для исследуемого материала, построенные при следующих условиях:

• 1.    время релаксации 79200 секунд, температура 25°С, начальная нагрузка на образец 2836 Н;

• 2.    время релаксации 600 секунд, температрура 30°С, начальная нагрузка на образец 1770 Н;

• 3.    время релаксации 600 секунд, температрура 70°С, начальная нагрузка на образец 1000 Н.

Известно, что вязкоупругие параметры, подставляемые в уравнения (1) и (2), будут давать на порядки разные результаты на ранних и поздних этапах протекания процесса релаксации. Поскольку нас интересуют продолжительные воздействия, то испытания при первом типе условий (наиболее длительные) проводились для определения начальных параметров, которые непосредственно будут применяться в качестве начальных при моделировании. Испытания при втором и третьем типе условий (кратковременные, но при разных температурах) проводились для оценки влияния температуры на параметры вязкоупругости. Результаты показаны на рисунках (Рис. 4, 5, 6; Fig. 4, 5, 6) и в таблице (Таблица1, Table 1).

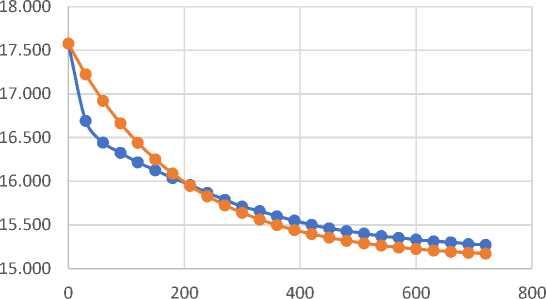
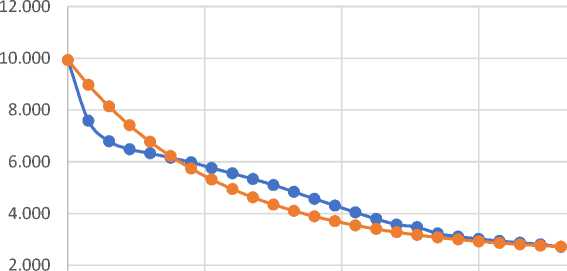
Полученные результаты наглядно показывают, что если мгновенный модуль упругости E 1 относительно незначительно меняется при повышении температуры до 70°С (снижается на 35%), то параметры E 2 и η меняются на порядки.

Таблица 1. Результаты определения вязкоупругих параметров Table 1. Results of viscoelastic parameters identification

Условия определения	Время, с	Температура, °С	E 1 , МПа	E 2 , МПа	η, МПа*с
1	79200	25	3300	31500	3.35*10^8
2	600	30	3280	20100	4.55*10^6
3	600	70	2150	700	6.25*10^5

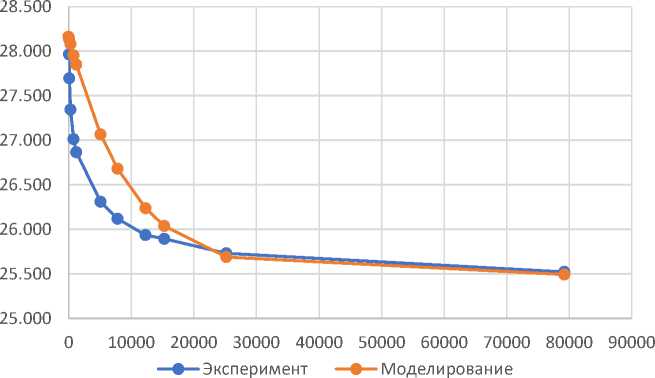
Рис. 4 – Экспериментальная и аппроксимационная кривые релаксации (при условиях №1).

Fig. 4 – Experimental and approximation relaxation curves (under conditions №1).

Эксперимент       Моделирование

Рис. 5 – Экспериментальная и аппроксимационная кривые релаксации (при условиях №2).

Fig. 5 – Experimental and approximation relaxation curves (under conditions №2).

0.000

0             200            400            600            800

Эксперимент       Моделирование

Рис. 6 – Экспериментальная и аппроксимационная кривые релаксации (при условиях №3).

Fig. 6 – Experimental and approximation relaxation curves (under conditions №3).

В результате основного эксперимента на циклическое термомеханическое воздействие были получены графики изменения суммарных напряжений в образцах на стадиях нагрева и охлаждения в течение 15000 секунд. Всего было выполнено 6 полных циклов нагрева и охлаждения, каждый цикл нагрева до 61°C продолжался 1500 секунд, охлаждения до 25°C – также 1500 секунд.

Для апробации и сопоставления с экспериментом реализация предложенной методики моделирования циклического термомеханического воздействия была выполнена в виде кода в академической версии математического пакета MathCAD 14.

В качестве начальных условий были приняты следующие:

• -    вязкоупругие параметры при 25°C E1=3300 MPa, E2=31500 MPa, η=3.35*10⁸ MPa*s;

• -    мгновенный модуль упругости при 61°C E1=2650 MPa;

• -    шаг по температуре был принят равным 10°C ;

• -    осредненный коэффициент температурного расширения CTE был принят равным 4.53*10-5 K-1.

Исходя из разницы между модулями упругости при температурах 25 °C и 61°C и принятого шага по температуре рассчитывается общее количество ячеек, на которое разбивается модель, в принятом варианте оно составило n = 26. Из этих 26 ячеек 5 последовательно выключатся при нагреве от 25°C до 61°C, а 21 останутся включенными и будут определять жесткость при 61°C. Такой подход предполагает допущение о линейной зависимости модуля упругости от температуры, что до достижения температуры стеклования для данного полимера не приведет к серьезным погрешностям.

Для сопоставления расчеты выполнялись в двух постановках при следующих допущениях:

С использованием предлагаемой многоэлементной модели

деформации в отключенных ячейках развиваются по закону обратной ползучести описано в [29]:

виртуальные как это было

₍ ( T-T)H )

S v ( T ) = ( S o - 7 ° ) • e ^{E 1} m

E i

С использованием предлагаемой многоэлементной модели, но

виртуальные

деформации в отключенных ячейках развиваются без учета обратной ползучести (т.е. полностью упруго):

S v^{( т} ) = O o - 7 ° ) E i

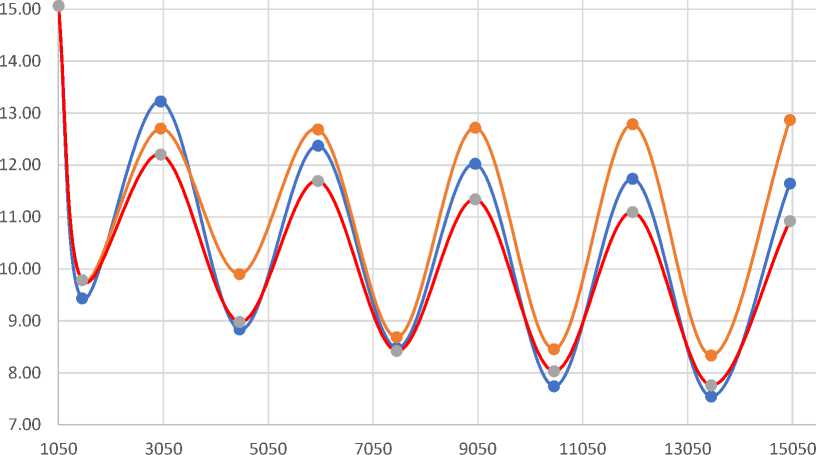
Результаты расчетов показаны на рисунке ( Рис. 7, Fig. 7 ), там же показаны и результаты эксперимента. Основной интерес, с нашей точки зрения, представляет сопоставление результатов моделирования с использованием предложенного подхода и результатов эксперимента.

16.00

Эксперимент Расчет по модели 1 Расчет по модели 2

Рис. 7 – Экспериментальная и расчетные графики зависимости напряжений от времени при цикоическом термомеханичсеком воздействии

Fig. 7 - Experimental and calculated graphs of stress dependence on time under cicoic thermomechanical action

В целом следует отметить, что совпадение результатов эксперимента (учитывая его непростую постановку и сложное механическое поведение исследуемого материала) с результатами моделирования можно считать удовлетворительным при обоих вариантах исходных предпосылок.

Результаты моделирования в первой постановке дают несколько завышенные результаты напряжений по сравнению с экспериментом, разница возрастает с увеличением количества циклов нагрева – охлаждения. Это можно объяснить тем, что в данной постановке происходит слишком значительное накопление остаточных напряжений от виртуальных деформаций, которые развиваются по закону обратной ползучести (т.е. постоянно накапливаются со временем). На графике это выражается в постепенном увеличении напряжений при охлаждении до 25°C, чего не наблюдалось в эксперименте.

Во второй постановке, когда при выключении ячейки реализуется только обратная упругая деформация, которая не развивается во времени и не дает постоянного значительного прироста напряжений от замораживаемых деформаций, напряжения напротив несколько занижены по сравнению с экспериментом. При этом напряжения снижаются с увеличением количества циклов нагрева – охлаждения, что качественно совпадает с экспериментом.

В итоге истинные значения напряжений лежат где-то между результатами, полученными при моделировании в первой и второй постановках. На наш взгляд объяснением данных результатов является то, что во второй постановке при вычислении виртуальных деформаций мы не учитываем экспоненту и, как следствие, не учитываем этом вязкость, которая входила в степень экспоненты. При этом в первом подходе мы предполагаем линейное изменение вязкости с температурой по аналогии с изменением мгновенного модуля упругости, а как мы показали выше

( Рис.4, 5, 6; Fig. 4, 5, 6 ) это крайне грубое допущение с учетом того, что коэффициент вязкости с увеличением температуры может меняться на порядки (как и упругий параметр E 2 ).

Таким образом, с учетом полученных результатов мы можем выдвинуть гипотезу, что для получения более точного результата при использовании предлагаемого подхода необходимо для параметров η и E 2 применять собственные законы зависимости от температуры, а не просто делить их так пропорционально E 1 (как это делалось в предыдущих работах [7,29]). Этот подход необходимо будет проверить в будущем.

• 4    Conclusions

В качестве основных полученных результатов можно выделить следующее:

• 1.    Предложена и апробирована структурная многоэлементная модель вязкоупругого материала с возможностью учета накопления остаточных напряжений.

• 2.    Предложен подход с использованием данной модели к прогнозированию формирования напряженно-деформированного состояния термопластичного полимера при циклическом термомеханическом воздействии. Результаты моделирования в двух постановках достаточно хорошо совпадают с результатами проведенного эксперимента:

  • 2.1.    При моделировании в первой постановке (с учетом обратной ползучести выключенных ячеек модели) максимальная разница с экспериментом по напряжениям составила 11%, при этом разница возрастала с увеличением циклов нагрева – охлаждения.

  • 2.2.    При моделировании во второй постановке (без учета обратной ползучести выключенных ячеек модели) максимальная разница с экспериментом по напряжениям составила 6%, при этом характер кривой зависимости напряжений от времени качественно более соответствовал экспериментальному, чем при моделировании в первой постановке.

В результате проделанной работы разработана и апробирована методика проведения эксперимента на циклическое термомеханическое воздействие на термопластовый полимер. Экспериментальные исследования выполнены на нетиповом специально разработанном и изготовленном оборудовании, которое обладает основным преимуществом перед аналогами – доступностью по стоимости при приемлемых по точности результатах.

Намечены пути для дальнейших исследований, в том числе развития предлагаемого подхода и его распространения не только на однородные полимерные материалы, но и на композиты с полимерной матрицей. Также целесообразным представляется модификация модели, чтобы она могла учитывать скачкообразный переход в высокоэластичное состояние при достижении температуры стеклования.

• 5    Fundings

  Проект выполнен при поддержке Российского научного фонда, грант №23–29–00425 https://rscf.ru/project/23-29-00425/

  The work was funded by the Russian Science Foundation, grant №23–29–00425 https://rscf.ru/project/23-29-00425/

• 6    Conflict of Interests

The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.