Структурно-скейлинговые переходы и универсальность статистики флуктуаций при пластическом течении металлов

Системы с так называемой «медленной динамикой» вызывают в последнее десятилетие большой интерес в связи с универсальными признаками их динамического поведения, обусловленного длинно-корреляционными многомасштабными взаимодействиями. Примерами таких систем служат жидкости в условиях турбулентности, биологические системы, пластически деформируемые кристаллические твердые тела. Особенностью их поведения является универсальность статистики

флуктуаций (статистическая автомодельность), которая впервые установлена при обработке случайных последовательностей флуктуаций электрической мощности, затрачиваемой на поддержание течения, в инерционном интервале турбулентности в условиях теста Кармана [1, 2]. Современные экспериментальные и теоретические исследования показывают, что пластическое течение кристаллических (поликристаллических) материалов сопровождается большими пространственновременными флуктуациями полей деформаций («прерывистое» пластическое течение — jerky flow), статистические характеристики которых обнаруживают признаки масштабной инвариантности [3]. Одновременно для ряда металлов и сплавов появление флуктуаций полей деформаций сопровождается стохастической динамикой напряжений пластического течения. Традиционные подходы в теории пластичности рассматривают данные явления как неустойчивость деформирования вследствие аномального деформационного разупрочнения, локализованного на масштабах ~10–100 мкм в виде полос скольжения, появление которых сопровождается конечно-амплитудными флуктуациями напряжений пластического течения и формированием нерегулярной, с признаками стохастической динамики, диаграммы пластического течения. Наблюдаемая пространственно-временная эволюция полос локализованного сдвига зависит от механизмов, определяющих коррелированное развитие последних на различных стадиях пластического течения. Изучение развития полос локализованного сдвига в кристаллах с использованием высокоскоростной съемки поверхностного рельефа и последующий анализ статистики полос локализованного сдвига, проведенные в работе [3], установили различную стохастическую динамику флуктуаций напряжений пластического течения, характеризующуюся конечными значениями корреляционной размерности стохастических пульсаций амплитуд в диапазоне умеренных скоростей деформаций, а также то, что флуктуации напряжений в области высоких скоростей деформаций описываются степенным законом. Стохастическое поведение типично для систем, обладающих самоорганизованной критичностью (Self-Organized Criticality — SOC) [4], основным признаком которой является именно то, что спектр (временной и пространственный) флуктуирующего параметра имеет степенной вид. Наличие этого признака у пластически деформируемых кристаллов [3] позволяет заключить, что при увеличении скоростей деформирования «прерывистое» пластическое течение переходит от режима стохастической динамики к режиму SOC-статистики [4]. Эти переходы традиционно наблюдаются в ситуациях, когда времена структурной релаксации, определяющие пластическое течение, приближаются к характерным временам нагружения. Обозначенные сценарии пластического течения допускают предположение о принадлежности процессов структурных превращений в деформируемых кристаллах к классу критических явлений, следствием чего и может быть универсальность статистики флуктуаций (статистическая автомодельность).

Автомодельность — важный признак эволюции многих нелинейных систем в случае сильно коррелированного поведения их подсистем, когда спектр флуктуаций на многих масштабах (от микроскопического a до некоторого структурного ξ ) демонстрирует «аномалии размерности» и фрактальные свойства [6]. В реальных системах структурный масштаб ξ ограничен макроскопическим масштабом L , позволяющим определить интервал масштабов между a и L , в котором может быть реализовано аномальное деформационное поведение. Такое поведение свойственно критическим явлениям, системам с самооганизованной критичностью. По аналогии с турбулентностью эти конечно-размерные критические системы могут быть названы «инерционными системами», а диапазон масштабов между a и L — «инерционным интервалом». Отличительным свойством рассматриваемых систем является тот факт, что они не могут быть разделены на статистически независимые мезоскопические области. К тому же данные системы не удовлетворяют основному положению «центральной предельной теоремы» теории вероятностей, и, как следствие, пространственно осредненные величины (с гауссовой статистикой флуктуаций переменных относительно средних значений) не могут быть введены [6].

Настоящая работа посвящена изучению универсальности статистики флуктуаций, обусловленных коллективным поведением дефектов в пластически деформируемых кристаллических твердых телах. Развитая статистическая теория рассматривает новый тип критических явлений в ансамблях мезодефектов — структурно-скейлинговые переходы, и связывает динамику данных переходов, сопровождающих пластическое течение и переход к разрушению, с проявлениями самоорганизованной критичности. Эволюция структуры (термодинамика и кинетика ансамбля мезодефектов) описывается двумя параметрами порядка — тензором плотности дефектов (совпадающим по величине с деформацией, индуцированной дефектами) и параметром структурного скейлинга (описывающим масштабные переходы при формировании коллективных мод различной сложности в ансамблях мезодефектов). В работах [11, 12] показано, что динамика данных мод обеспечивает специфические механизмы переноса импульса и диссипации энергии, которые могут быть связаны с пластическим течением и локализацией дисперсного разрушения. Развитие неустойчивостей в конденсированных средах (турбулентности в жидкостях, «прерывистого» пластического течения) ассоциируются в [11, 12] с динамикой обсуждаемых коллективных мод.

2.    Универсальность статистики флуктуаций в инерционном интервале турбулентности

Экспериментальное исследование стационарной турбулентности (течение Кармана, реализуемое между двумя вращающимися с постоянной частотой дисками) [2, 7] выявило статистическую автомодельность, проявляющуюся в универсальности PDF флуктуаций электрической мощности P ( t ) , подводимой к дискам для поддержания течения. Флуктуации мощности в диапазоне двух порядков числа Рейнольдса в области полностью развитой турбулентности приведены на рисунке 1, взятом из работы [2]. В [2] также показано, что универсальность в распределении флуктуаций сопровождается резким падением мощности, инжектируемой в поток, что связывается с генерацией когерентных структур на макроскопическом масштабе системы (на расстоянии между дисками). Негауссовый характер ветвей распределения связывается с развитием когерентно эволюционирующих флуктуаций, инициируемых некоторым единым механизмом. Отклонение распределения от гауссового и соответствие его степенному закону представляют интерес в связи с аналогиями поведения параметров порядка в критических системах [8]. Важной чертой эволюции электрической мощности является «медленная динамика» ее безразмерных флуктуаций ( P - ( P )/о P , (где скобки ( ) _{2         2} 12

обозначают осреднение по времени, ст P = ( \Р )- \Р / ) — среднеквадратическое отклонение) при увеличении числа Рейнольдса по сравнению с поведением некоррелированных степеней свободы. Коррелированность наблюдается в широком диапазоне амплитуд подводимой мощности. Сопоставление эволюции мощности с поведением критических систем допускает, что генерация когерентных структур есть следствие сильного взаимодействия между коллективными модами на широком спектре масштабов, что характерно для критических явлений [6]. Показано, что микроскопически различные системы обнаруживают близкую статистику, что свидетельствует о существовании некоторого класса «универсальности» применительно к «конечномерным критическим системам».

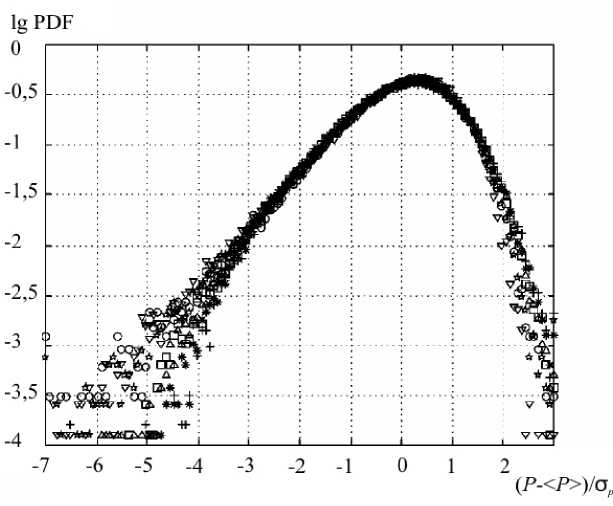
Рис. 1. Функция плотности распределения флуктуаций мощности при различных числах Рейнольдса:

+ - 15,169; * - 70,791; о - 111,240; □ - 212,370; △ -333,750; V - 318,560; * - 500,590 [2]

Теоретическое исследование двумерных спин-решеточных моделей позволило установить, что PDF для данных систем представляется с высокой точностью в виде [6]:

П ( y ) = K ( e ⁽ y) ^- e x ⁽ y ) ) a .

Здесь K , b , 5 — некоторые эмпирические константы; x = b ( y - s ) ; a = n( 2;

y = ( m - m ) )/o _m , где   (m^

среднее значение флуктуирующего параметра, оm — среднеквадратичное отклонение.

В работе [9] проведено численное исследование турбулентности течения Кармана на основе динамической нелинейной решеточной модели со структурой гамильтониана, по форме близкой к потенциалу Френкеля–Конторовой. Анализ результатов также показал «подчиненность» статистики флуктуаций данному виду PDF.

Рассмотрение динамики «частиц» в «нелинейной решетке» выявило генерацию локализованных конечно-амплитудных мод, так называемых «дискретных бризеров» — коллективных мод микросдвигов с нулевой скоростью распространения фронта [9]. В результате стало возможным считать, что динамика бризеров, аналогичная динамике локализованных мод дисторсии (дислокаций и дисклинаций), может иметь отношение к развитию турбулентности. Сделанное предположение согласуется с замечанием Френкеля [10] о том, что природа динамических процессов в жидкости как конденсированной среде в большой степени подобна природе динамических явлений в твердых телах, в которых механизм переноса импульса ассоциируется с движением мезоскопических носителей (дислокаций, дисклинаций), представляющих собой «локализованные дисторсии» с признаками волновой динамики.

3.    Структурно-скейлинговые  переходы как механизм самоорганизованнойкритичности в мезоскопических системах

Нелинейная динамическая «решеточная» модель турбулентности [9] находится в соответствии со сценарием развития турбулентности как нового класса критических явлений — структурно-скейлинговых переходов, характерных для широкого класса неравновесных мезоскопических систем, обнаруживающих признаки «медленной динамики». Микроскопические параметры порядка таких систем и соответствующий им лагранжиан введены в работе [11] и описывают развитие локализованных неустойчивостей, определяемых локализацией соответствующей группы симметрий тензора дисторсии. Локализованные моды дисторсии, динамика которых обеспечивает перенос импульса в конденсированной среде, могут быть введены как независимые переменные, отражающие структурные изменения в термодинамических, динамических и стохастических свойствах рассматриваемых систем.

Если допустить, что локализованные моды дисторсии есть дефекты в динамической системе, то генерацию и развитие этих мод можно отождествить с локальными изменениями симметрийных свойств среды. С учетом этого аспекта параметры, соответствующие локализованным модам дисторсии, вводятся в [11] как компоненты интенсивности калибровочного поля θ_µν и α_µν , связанные, соответственно, с локальными ротациями Γ_µ и трансляциями β_µ в общем представлении ковариантных производных полной дисторсии среды

D x=∂ x+Γ x+β .

Тогда лагранжиан системы может быть записан в виде:

1 (1)(1)            1 (2)(2)

L ^=- 2 C 1 g µλ g νχ α µν α λχ ^- 2 C 2 g µν g νχ ^θ µν ^θ λχ ,                                          (1)

где   θµν = ∂µΓν - ∂νΓµ + ΓµΓν - ΓνΓµ;   αµν=∂µβµ-∂νβν+Γµβν-Γνβµ+θµνx;   gik   — компоненты метрического тензора; C1 и C2 — материальные константы.

Принимая во внимание кинематику неустойчивостей течений в жидкостях и при пластической деформации в твердых телах, аналогичным работе [11] образом введем микроскопические параметры, определяющие локализованные моды дисторсии. Первый их них — микроскопический тензор локализованного сдвига sik = 1/2s(vilk + livk). Здесь 5 = SdB — интенсивность сдвига на площадке Sd = Sd V с вектором сдвигового смещения (вектором Бюргерса) B = bl, где l, V — единичные вектора, определяющие ориентацию площадки и направление сдвига соответственно. Макроскопический тензор локализованных сдвигов pik  определяется осреднением  sik  по статистическому ансамблю микроскопических  сдвигов: pik = nsik , где  n  — концентрация микросдвигов.

Решение статистической задачи, основанное на представлении лагранжиана в форме (1), показало существование дополнительного параметра порядка δ — параметра структурного скейлинга, для континуума с локализованными дисторсиями. Данный параметр представляет отношение двух характерных масштабов в среде с мезодефектами δ ~ (R r0 )3 , где r0 — характерный размер зародышей дефектов, R — расстояние между дефектами. В случае простого сдвига ( с = сxz, p = pxz) из решения получены три характерных нелинейных зависимости pik от напряжения для различных значений параметра структурного скейлинга 5 (5 >5* »1,3; 5 c <5<5*; 5<5 c *1, где 5 c, 5* — точки бифуркации решения) (Рис. 2). Точки бифуркации 5c, 5* играют роль, аналогичную критическим температурам в теории фазовых переходов Ландау.

Параметр структурного скейлинга 5 имеет смысл второго параметра порядка, и его значение определяет условия «термализации» мезоскопической неравновесной системы в терминах «эффективных температур» для систем с «медленной динамикой» [15].

Статистический подход дал возможность записать мезоскопический неравновесный потенциал, описывающий развитие локализованных дисторсий при различных сценариях, связанных с типами нелинейности самого потенциала, и представляющий «минимальное разложение» для неравновесной свободной энергии. Потенциал задается полиномом 6-й степени и имеет форму, подобную форме разложения Гинзбурга–Ландау [11]:

F = - A ( 5 , 5 * ) p ² - - Bp ⁴ + - C ( 5 , 5 с ) p ⁶ - D a p + x ( V i p ) . (2) 246

Градиентный член в выражении (2) отвечает за эффекты нелокальности в ансамбле взаимодействующих микросдвигов; A, B, C, D и x — параметры, характеризующие нелинейные и нелокальные свойства континуума с взаимодействующими микросдвигами. Кинетика параметров порядка pik и 5 задается известным эволюционным неравенством dF[ tt = p dF ^ Qp + 5 dF/d5< 0, откуда dp = —Г p [ A (5, 5*) p - Bp3 + C (5, 5с) p5 - Da-Vi (xViP)],

d 5 f 1 aA  2 1 d CД

— = -Г--pp dt     4 2 55    6 d5J

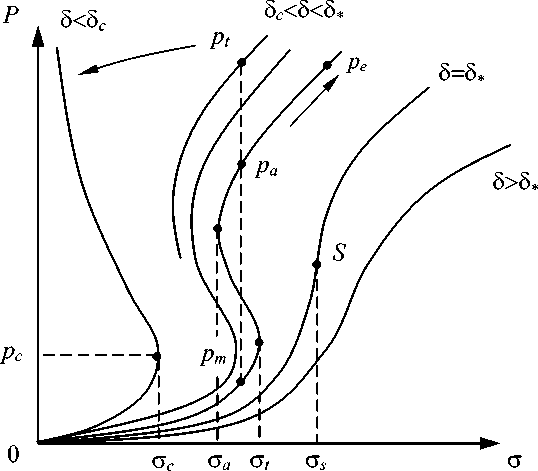
Рис. 2. Характерные нелинейные реакции среды на рост локализованных сдвигов в зависимости от значений параметра структурного скейлинга 5

Здесь Г p и Г ₅ — кинетические коэффициенты. Как это следует из решения уравнения (3), переходы через точки бифуркации 5 c и 5 * приводят к резкому изменению типов коллективных мод для тензора p_ik . Сценарии переходов определяются групповыми свойствами уравнений, которые различны для разных интервалов значений параметра структурного скейлинга.

Качественные изменения в поведении системы иллюстрируются семействами гетероклиник, соответствующих уравнению (3) при различных значениях 5 (Рис. 3). В области 5 > 5 * (сплошные линии) решения определяются спектром собственных форм в виде пространственно-периодических мод дисторсии S 1 на масштабах Л со слабой ориентационной анизотропией свойств, зависящих от действующего напряжения о . При 5 > 5. и пересечении сепаратрисс (пунктирная линия) собственные формы уравнения (3) претерпевают качественное изменение свойств, сопровождающееся расходимостью внутреннего масштаба Л : A»- ln ( 5-5 * ) . Периодические решения при этом трансформируются в конечно-амплитудные структуры, имеющие форму «бризеров» в области 5 > 5 * при 5^5 * , и автосолитонные моды вида p ( Z ) = P ( x - Vt ) в области выраженной ориентационной метастабильности 5 с < 5 < 5 * , на фронтах которых формируются коллективные ротационные моды S ₂ . Амплитуды автосолитонных волн p , скорости волновых фронтов V и ширина волновых фронтов L_S определяются параметрами неравновесного перехода:

Р = 2(Ра -Pm)[1-th(zLs 1)],

4 ( 2 %/ A f

S " (Pa - Pm ) ,

X ^{A (} P a - P m )

=      Г P2      ’ где (Pa - Pm ) — скачок значения P в области метастабильности (Рис. 2).

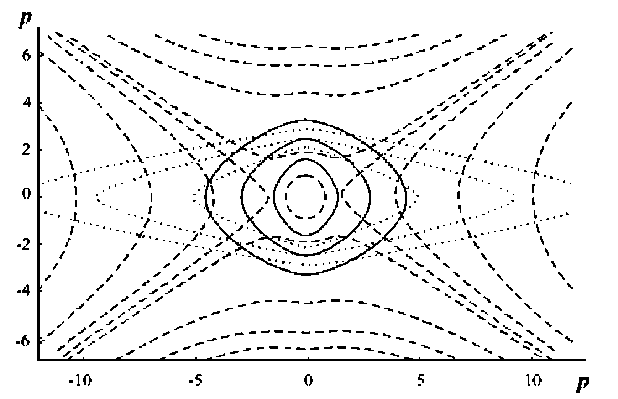
Рис. 3. Типы гетероклиник для областей: 5 < 5 с (штриховая линия); 5 > 5 * (сплошная линия); 5 с < 5 < 5 * (пунктирная линия)

Формирование бризеров представляет собой переходный режим, который предшествует генерации коллективных мод автосолитонного типа, обеспечивающих качественно новый механизм переноса импульса в среде. Переход через точку бифуркации 5 c сопровождается формированием пространственно-временных структур микросдвигов качественно нового типа (Рис. 3, штриховая линия), описывающих взрывную кинетику развития ансамбля микросдвигов при t ^ t f на спектре пространственных масштабов (диссипативные структуры обострения S ₃ ) [12]:

р ⁽ x , t ) = ^{ф (} t ) ^f (0; ^z = x ф ( t ) ; ^{ф (} t )~ ( t ^- t f ) m ; ф ( t ) ~ ( t ^- t f ) d , ⁽⁶⁾

где m , d — параметры, определяющие тип нелинейности уравнения (3) для 5<5 с , p >  р с (см. Рис. 2); t f — характерный временной масштаб автомодельного решения (6).

В зависимости от значений параметров m , d существует три типа автомодельных решений вида (6). Случай для d = 0, так называемый S -режим [13], представляет особый интерес, когда автомодельное решение имеет вид:

р ⁽ x , t ) = ^[ C ( ⁵ , ⁵ с ) ⁽ t ^- t f ) ] m 2 ^ 1 + ^ )sin² ± 1 _{+ л6} , ⁽⁷⁾ ( ^{( 1 + 2} m ) I, Lf ))

где 0 — случайное значение в интервале (0, 1). Вид функции f ( Z ) находится из решения соответствующей задачи на собственные значения. Масштаб L_f , так называемая фундаментальная длина [12, 13], имеет смысл пространственного периода решения (7):

Lf = 2пm((1/m + 1)хC 1 (5, 5с))Z .

Автомодельное решение (7) описывает кинетику ансамбля микросдвигов в режимах обострения р ( x , t ) ^да при t ^ t f на спектре пространственных масштабов L H = kL_f ( к = 1,2,..., K ). Возможно появление сложных структур обострения на масштабах L_H = kL f , когда расстояния между так называемыми простыми структурами будет приближаться к L_f .

Сценарии самоорганизованной критичности, реализуемые в соответствии с кинетикой структурно-скейлинговых переходов, определяются классами универсальности автомодельных решений (5) и (6), что и позволило предложить в [14] интерпретацию поведения систем в инерционном и диссипативном интервале турбулентности.

4.    Универсальность статистики флуктуаций при неустойчивом пластическом течении металлов

При обсуждении аналогий в механизмах развития турбулентности в жидкостях и пластического течения в металлах в [11, 12] эти явления связываются с признаками универсальности, характерными для нового класса критических явлений —

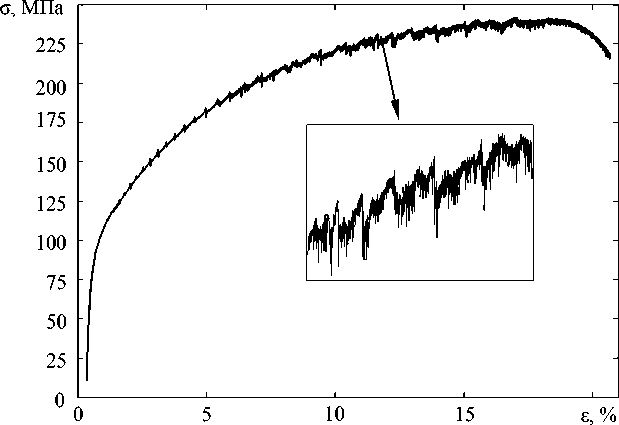
Рис. 4. Деформационная диаграмма алюминиевого сплава Al 5454

структурно-скейлинговых переходов, в основе которых лежат длинно-корреляционные взаимодействия в ансамблях микросдвигов. Формирование коллективных мод микросдвигов в форме автосолитонных структур может приводить к зарождению локализованных вихрей и областей локализации пластической деформации — полос локализованного сдвига [14].

Изучение статистики флуктуаций напряжений течения, обусловленных формированием зон локализации деформации, проводилось на гладких образцах сплава Al–Mg, армко-железе и сталях при комнатных температурах. Деформационная диаграмма алюминиевого сплава представлена на рисунке 4 и демонстрирует множественные флуктуации напряжения течения.

Квазистатическое нагружение гладких образцов алюминиевого сплава (диаметр 10 мм, рабочая длина 100 мм) осуществлялось при комнатной температуре (~300 К) при контролируемых перемещениях со скоростью нагружения 0,3 мм/c, что обеспечивало скорость деформации 10-4 с-1 . Оцениваемая погрешность в определении напряжений не превышала ±0,1%. Регистрация данных осуществлялась с частотой 15 Гц.

Вычисление PDF флуктуаций напряжения пластического течения подтверждает универсальный вид статистического распределения (Рис. 5) и, как следствие, масштабную инвариантность механизмов, обеспечивающих перенос импульса на этой стадии.

Самоподобное автосолитонное волновое решение (5), которое получено для кинетики микросдвигов в области значений параметра структурного скейлинга 5 c < 5 < 5 * , определяет характерный универсальный класс коллективных мод, которые обеспечивают универсальность PDF при пластической деформации как конечномерном критическом явлении. Многочисленные флуктуации напряжения, по-видимому, являются следствием формирования множественных самоподобных автосолитонных волновых структур вдоль образца.

На рисунке 6 представлена характерная диаграмма деформирования армко-железа в условиях одноосного сжатия при температуре 300 К.

Функции распределения флуктуации напряжения для алюминиевого сплава, армко-железа и стали представлены на рисунке 6 для масштабированных флуктуаций 2          ²¹²

напряжения 1 о-^оШ^а D , где ° D = (\ ^а/ W/ ) •

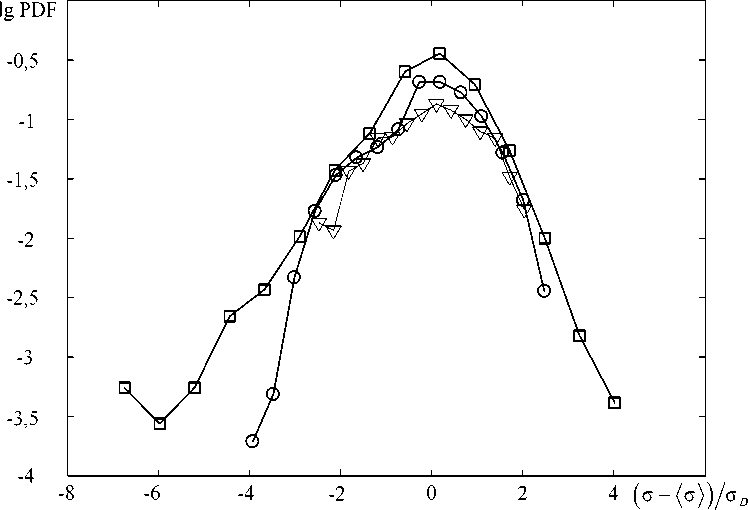
Рис. 5. Плотность распределения флуктуаций напряжения на стадии пластического течения для различных материалов (□ - сплав Al 5454; о - сталь 03Х18Н10; V - армко-железо)

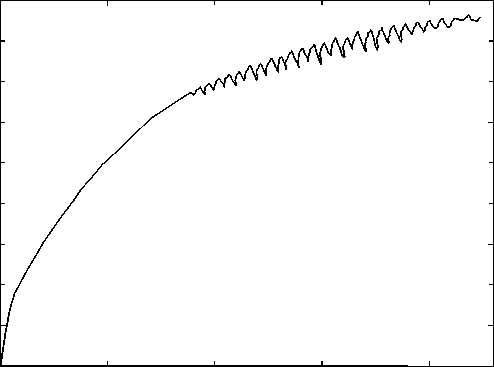
σ, МПа

0          0,05        0,1         0,15        0,2 ε, %

Рис. 6. Характерная диаграмма деформирования армко-железа

Экспериментальные кривые показывают явное статистическое самоподобие в виде универсальности PDF. Отсюда следует, что процесс развития неустойчивостей при пластическом течении — это конечномерный критический процесс, связанный с характерным «универсальным классом».

5.    Обсуждение результатов

С точки зрения традиционных феноменологических теорий пластичности кристаллических материалов пластическая деформация рассматривается как квазиламинарное течение квазиоднородного континуума, при этом пластическое течение считается пространственно-однородным в объеме образца. Это означает, что флуктуации не проявляют себя на масштабах, превосходящих представительный объем (объем осреднения), который предполагается, в свою очередь, существенно меньшим объема образца. Тогда пространственно-временные эффекты, сопровождающие неоднородность пластического течения, происходят в случае, если деформационные процессы макроскопически неустойчивы, например, при деформационном разупрочнении. В отличие от классического сценария, в данной работе наблюдаемые макроскопические неустойчивости представляются как пространственно-временные структуры с динамикой распространяющихся автосолитонных волн или стохастических деформационных мод.

Парадигма устойчивого пластического течения находится, фактически, в противоречии с современными представлениями физики пластического течения кристаллических материалов, согласно которым механизмы переноса импульса при пластическом течении соотносятся с дискретным движением дефектов дислокационного типа. Как следствие, возникает новая картина пластического течения: вместо некоррелированного движения дислокаций появляются множественные локализованные конечно-амплитудные моды, развитие которых определяется длинно-корреляционными взаимодействиями. Зарождение и развитие областей деформирования, соответствующих данным модам, ассоциируется с механизмами пластической неустойчивости качественно нового типа, характеризующимися сменой детерминированных пространственновременных осцилляций деформации на стохастические моды локализованной пластичности («прерывистое» течение). «Прерывистое» пластическое течение металлов и сплавов является уникальным явлением для исследования свойств, обусловленных длинно-корреляционными взаимодействиями в неравновесных системах, обнаруживающих «медленную динамику». В соответствии с дискретной природой носителей, обеспечивающих перенос импульса (дислокаций, дислокационных субструктур), динамика течения и статистка флуктуаций напряжений анализируются с помощью вводимых временных и пространственных инвариантов, характеризующих морфологию поверхностного рельефа в присутствии множественных полос локализованного сдвига и временную статистику флуктуаций напряжений пластического течения.

В работе показано, что:

• –    статистическая универсальность флуктуаций напряжений пластического течения в терминах PDF может быть связана с автомодельной природой коллективных мод мезодефектов — автосолитонных мод, генерируемых ансамблями микросдвигов на широком спектре масштабов;

• –    существование пространственно-временных инвариантов является следствием автомодельной природы коллективных мод, «контролирующих» динамику мезоскопической системы в условиях структурно-скейлинговых переходов;

• –    механизм самоорганизованной критичности, относящийся к структурно-скейлинговым переходам, обусловлен существованием и динамикой специфического параметра порядка — параметра структурного скейлинга, характеризующего масштабные переходы при генерации коллективных мод ансамблей мезодефектов (коллективные моды определяют текущие степени свободы, ассоциируемые в случае пластического течения с полосами сдвига);

• –    подобно критическим явлениям в инерционном интервале турбулентности, неустойчивости при пластическом течении представляют также критическое явление, развивающееся на конечных масштабах при формировании множественных коллективных мод, принадлежащих к одному классу универсальности, определяемому видом автомодельного решения.

Авторы благодарят Didier Sornette за плодотворное обсуждение результатов работы.

Работа выполнена при поддержке Российского фонда фундаментальных исследований (проекты № 05-01-00863_а,      № 07-01096004-р_Урал_а,

№ 07-01-91100-АФГИР_а).