Структурное моделирование развития поврежденности в дисперсно наполненных эластомерных нанокомпозитах с учетом межфазных взаимодействий

Дисперсно наполненные эластомеры являются одним из наиболее распространенных полимерных конструкционных материалов, которые на сегодняшний день широко применяются в самых разных отраслях промышленности (при изготовлении резин различного назначения, автомобильных шин, твердых ракетных топлив, демпферов и амортизаторов и другого). Эти композиты относятся к материалам с хорошо выраженной механической неоднородностью структуры, так как состоят из относительно мягкой высокоэластичной каучукоподобной матрицы и внедренных в нее значительно более жестких и прочных частиц наполнителя.

Композиты, в зависимости от их конкретного предназначения, могут иметь разнообразные наполнители. Самыми известными являются черная и белая сажи (технический углерод и гидратированный диоксид кремния соответственно) [1–3]. В то же время в современных рецептурах активно используются и другие материалы, например, графены, фуллерены, нанотрубки, наноалмазы [4–8]. Наполненные эластомеры также служат объектом интенсивных теоретических исследований с целью получения зависимостей между их физико-механическими свойствами на макроуровне и внутренним строением на микро- и наноуровнях [9–17].

2.    Предмет исследований

Совокупный опыт, накопленный в результате научного поиска, позволил выделить две наиболее интересные особенности эластомерных композитов: 1) способность накапливать при деформировании значительную внутреннюю поврежденность, сохраняя без заметных потерь свою работоспособность [18, 19]; 2) упрочнение (разрывные усилия увеличиваются в 5–15 раз, а предельные деформации в 2–4 раза) [20–22]. Несмотря на широкую и давнюю известность этих эффектов, однозначного мнения, почему они имеют место, не существует, и объяснить их с точки зрения классической механики на сегодняшний день так и не удалось.

Большинство исследователей сходится на том, что при деформировании эластомерного композита частицы наполнителя создают в материале огромное количество равномерно распределенных микроразрывов, способствующих переводу каучуковой матрицы из сложного (трехосного) напряженного состояния в систему многочисленных одноосно нагруженных волокон — тяжей, ориентированных вдоль направления действия внешней нагрузки, то есть наиболее полезным образом. Возникающие в результате такой структурной перестройки микроскопические волокна представляют собой цепочки из жестких частиц, скрепленных «связанным» (то есть одноосно ориентированным) каучуком. Поэтому для волокон разрывные усилия должны быть гораздо выше соответствующих величин для того же эластомера, но в обычном (неориентированном) состоянии. Эксперименты по непосредственному определению прочности тонких эластомерных волокон однозначно свидетельствуют, что чем меньше диаметр волокна, тем выше его прочность [23]. На микро- и наноуровне этот эффект проявляется еще сильнее [24, 25]. Наличие микро- и нановолокон в дисперсно наполненных эластомерах подтверждается экспериментальными исследованиями [26–30]. В работах [31–34] показано, что переориентация играет исключительно важную роль в формировании свойств эластомерных нанокомпозитов.

Вторым фактором, который может существенно повлиять на механические свойства эластомерного композита, является то, что частицы наполнителя (особенно наноразмерные) имеют огромную поверхность межфазных контактов, за счет которых прилегающая к ним матрица приобретает связанное более жесткое и прочное состояние. Известно достаточно большое количество публикаций о том, что такие поверхностные слои связанного эластомера играют основную роль в формировании механических свойств материала [35–40]. Имеются работы, в которых высказываются предположения о существовании вблизи частиц наполнителя не одного, а нескольких приповерхностных слоев с особыми свойствами [41–43]. Методами ядерного магнитного резонанса получена информация, свидетельствующая о существовании тонких стеклообразных слоев на активном наполнителе [44–46].

Теоретические модели, описывающие влияние слоев на частицах наполнителя на макросвойства эластомерных композитов даны [47–52].

Таким образом, можно констатировать, что процессы развития внутренней поврежденности в эластомерных композитах (системах с сильной структурной неоднородностью) протекают совсем не так, как в чистых эластомерах (структурно однородных материалах). Соответственно для их теоретического анализа требуются новые нетрадиционные модели, учитывающие эту специфику. Один из таких подходов представлен в данной статье.

3.    Структурная модель возникновения микротяжа в эластомерном композите

Теоретическое описание процесса зарождения и роста микротяжей в эластомерном композите при наличии на поверхности частиц наполнителя матричных слоев повышенной жесткости осуществлялось с помощью модернизированной структурной модели [53]. В ее основе лежит гипотеза о повышенной прочности эластомера при одноосном растяжении за счет переориентации молекулярных цепей в направлении действия нагрузки, то есть возникновения «прочностной анизотропии». Модернизация заключалась во введении в расчетную схему нескольких приповерхностных эластомерных слоев с различными жесткостями.

Для математической реализации данной идеи использовали «анизотропный» критерий появления микроразрыва в эластомере, учитывающий повышенную по сравнению с другими видами напряженного состояния прочность материала при одноосной вытяжке. Дело в том, что, в соответствии с известными на сегодня классическими подходами к разрушению материала, структурные микроповреждения должны появляться в наиболее напряженных местах, то есть в зазорах между близко расположенными частицами. Поэтому описать процесс зарождения и роста микротяжа с их помощью невозможно в принципе.

При расчетах предполагали, что возникновение повреждения в некоторой точке эластомерной матрицы происходит в момент, когда нарушается неравенство:

f ( X 1 , X 2 , X 3 ) = a| £ x - 2 - 3 | + e \ i = 1            7

, Xj . X2. X3    J

ln—ln—ln— <  1,

^X 2    ^X 3    ^X 1

где X 1 , X ₂, X ₃ — кратности главных удлинений. Функция f (деформационный прочностной критерий) содержит две безразмерные константы: a и р , определяющие прочностные свойства материала.

Их значения можно подобрать из экспериментов.

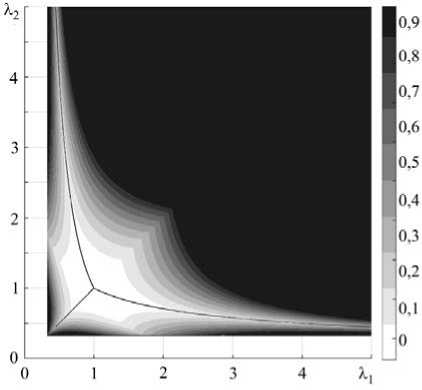
Рис. 1. Зависимости деформационного критерия f от X i , X 2 , X 3 для несжимаемой среды; сплошные линии соответствуют одноосному растяжению

Первое слагаемое положительно при любом деформированном состоянии    материала

(в отсутствие деформаций оно равно нулю). Второе слагаемое при одноосном растяжении материала также равно нулю, а при других видах напряженно-деформированного состояния дает дополнительный положительный вклад в функцию f , то есть «приближает» ее к критическому значению f = 1. Таким образом, критерий (1) удовлетворяет условию одноосной прочностной анизотропии: при одноосном растяжении он минимален по сравнению с другими напряженно-деформированными состояниями (при одних и тех же значениях инварианта       тензора        деформации

X^{- 2} + X^{- 2} + X^{- 2} = const).

На рисунке 1 представлена зависимость f от главных кратностей удлинения X 1 , X ₂, X 3

для несжимаемой упругой среды ( X 1 X 2 X 3 = 1). Значения констант a = 0,25 и р = 0,05 выбирались из соображений наилучшей

наглядности графика. В дальнейшем эти же величины использовались при компьютерном моделировании.

Сплошные линии соответствуют одноосному растяжению вдоль главных осей (горизонтальной — X 1 ,

вертикальной — X ₂, с наклоном в 45° — X 3 ). Анализируя картину распределения f , можно сказать, что одноосное растяжение способно достигать очень больших значений (светлые области), тогда как при других видах деформирования разрушение начнется значительно раньше (темные области).

При компьютерном моделировании эластомерный композитный материал представляли в виде регулярной прямоугольной решетки

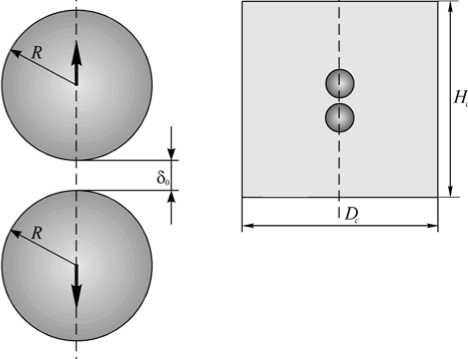
Рис. 2. Расчетная схема к задаче взаимодействия двух жестких сферических включений в нелинейно-упругой матрице

из одинаковых сфер, растягиваемой вдоль одной из осей симметрии. Если частицы наполнителя находятся достаточно близко друг к другу, то напряженно-деформированное состояние в зазорах будет близко к состоянию при парном взаимодействии жестких включений в «мягкой» упругой матрице (Рис. 2), когда соединяющая центры включений ось совпадает с направлением растяжения среды [12, 54]. При этом макроскопические кратности удлинений в композите можно вычислять как относительное изменение расстояния между центрами частиц.

Все расчеты проводились для элементарной композитной ячейки в виде эластомерного цилиндра, в центральной части которого на оси симметрии размещалась пара жестких сфер радиуса R . Включения располагались на расстоянии 50 друг от друга. Высота Hc и диаметр Dc цилиндра задавали равными 15R. Тем самым обеспечивалось условие отсутствия влияния удаленных границ на напряженно-деформированное состояние вокруг данной пары. Внешние границы структурной ячейки считались свободными от напряжений. Нагружение системы производили путем раздвигания сфер вдоль межцентровой оси на заданное расстояние 5. В качестве меры, характеризующей макроскопические деформации, использовалась величина X = (5 + 2R)/(50 + 2R) — кратность удлинения.

Известно, что силы взаимодействия между жесткими сферами в упругой матрице, очень большие при малых зазорах, резко падают по мере увеличения последних, и при расстояниях порядка своего характерного размера частицы практически перестают «чувствовать друг друга» [54]. Поэтому все модельные расчеты проводили для случая, когда начальный зазор между частицами 5 0 равнялся 0,4 R . Выбор этого значения был сделан из соображений, что на таком расстоянии градиенты напряжений в зазоре еще не столь велики, чтобы создавать технические сложности при решении задачи, и в то же время взаимное влияние частиц уже вполне достаточное для цели данной работы (моделирования процесса возникновения микротяжей).

Жесткость частиц наполнителя в упрочняемых эластомерных композитах, как правило, много выше, чем матрицы. Поэтому упругий модуль сферических включений E_p задавали равным 10 ⁴ E_m ( E_m — начальный модуль Юнга матрицы). То есть включения были практически недеформируемыми и, соответственно, неразрушаемыми. Повреждения могли появляться только в эластомере. При расчетах полагалось E m = 9 МПа (типичное для большинства промышленных эластомеров значение). Матрицу считали несжимаемой нелинейно-упругой средой, механические свойства которой описываются потенциалом Трелоара (потенциалом нео-Гука):

w = E m ( X 2 + X 2 + X 2 - 3 ) . (2)

Краевую нелинейно-упругую задачу решали в осесимметричной постановке методом конечных элементов (с помощью вычислительного пакета ANSYS, Лицензия ANSYS Academic Research Mechanical and CFD для ИМСС УрО РАН). Компьютерное моделирование процесса зарождения и роста микротяжа производилось следующим образом. В процессе пошагового нагружения цилиндрической ячейки (зазор между сферическими включениями на каждом шаге увеличивался на величину А5 , не большую, чем 0,08 R ), каждый конечный элемент проверялся на выполнение условия (1), и в случае f ( X 1 , X ₂, X 3 ) > 1 его жесткость уменьшалась до близкого к нулю значения. Тем самым имитировалось разрушение элемента и потеря им несущей способности.

• 4.    Результаты компьютерного моделирования

  • 4.1.    Моделирование образования микротяжа в эластомерном нанокомпозите

при отсутствии межфазных слоев

Ввиду больших сложностей с получением достоверной экспериментальной информации проблема межфазных контактов при деформировании нанонаполненных эластомеров на сегодняшний день еще слабо изучена. Поэтому при компьютерном моделировании возникновения и роста микротяжа рассматривалось два предельных варианта взаимодействия внутри ячейки: 1) абсолютная адгезия между матрицей и наполнителем; 2) эластомер свободно скользит по поверхности частицы, но без отслоения (для нанокомпозитов появление межфазных отслоений не характерно из-за огромных сил поверхностного натяжения, которые, как известно, пропорциональны кривизне поверхности (закон Лапласа)).

На рисунке 3 представлены нормированные поля распределения гидростатических напряжений ( ° hidrI E m ) и интенсивности напряжений ( □ int/ E m ), а также безразмерного деформационного критерия f для 1-го (Рис. 3 а – в ) и 2-го (Рис. 3 г – е ) вариантов межфазного контакта. Так как решалась осесимметричная задача, то на рисунках отображена только половина области. Показана ситуация, когда расстояние между центрами включений увеличилось в 1,7 раза, но поврежденные зоны еще не появились. На рисунках хорошо видно, что максимальные значения инвариантов напряжений и критерия f находятся в разных местах.

На рисунке 4 представлены поля распределения прочностного критерия f на разных стадиях формирования локального повреждения при полной адгезии между матрицей и включениями и при проскальзывании без отслоения. Белым цветом показаны разрушенные участки матрицы (полости вокруг микротяжа). Рисунки 4 а , г соответствуют моменту зарождения первичного повреждения.

Рис. 3. Поля распределения с _hidrlE_m

Cn^lEm.

полная

( а ),

и двух вариантах межфазного контакта:

проскальзывание матрицы по включениям без отслоения ( г )–( е )

( б ) и f ( в ) при Х = 1,7 (локальные повреждения отсутствуют) адгезия между матрицей и включениями ( а )–( в ); свободное

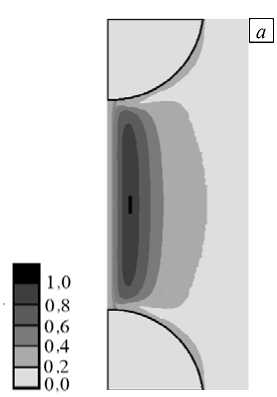
Рис. 4. Поля распределения f на разных стадиях формирования микротяжа при двух вариантах межфазного контакта: полная адгезия между матрицей и включениями ( а )–( в ); свободное проскальзывание матрицы по включениям ( г )–( е ); возникновение первичного повреждения при Х = 1,85 ( а ) и Х = 2,25 ( г ); микротяж в процессе формирования при Х = 2,02 ( б ) и Х = 2,35 ( д ); полностью сформированный микротяж при Х = 2,35 ( в ) и Х = 2,43 ( е )

Рис. 4. Продолжение

При абсолютной адгезии оно начиналось при Х = 1,88, а при проскальзывании критическое значение X увеличивалось до 2,25. На рисунках 4 б ( Х = 2,02) и 4 д ( Х = 2,35) представлены промежуточные стадии роста тяжа в момент, когда размер локальной полости разрушения составлял примерно половину от текущего зазора между частицами. То есть процесс локального разрушения при 2-м варианте начинался позже, но развивался быстрее, так что полное формирование микротяжа заканчивалось примерно при одной и той же макроскопической деформации: в 1-м варианте при Х = 2,35 (Рис. 4 в ), во 2-м при X = 2,43 (Рис. 4 е ).

• 4.2.    Моделирование образования микротяжа в эластомерном нанокомпозите при наличии межфазных слоев

Возникновение приповерхностных слоев большинство исследователей объясняют частичным осаждением полимерных молекул на частицы наполнителя, что уменьшает их подвижность и повышает жесткость слоя. Теоретическая оценка размеров таких слоев дает значения порядка от 2 до 10 нм [43], поэтому в микрокомпозитах с частицами микронных размеров их влияние на макросвойства должно быть незначительным. Но такие слои представляют серьезный интерес в нанонаполненных системах, в которых их толщина соизмерима с размером включений. В [55] теоретически изучена возможность отрыва

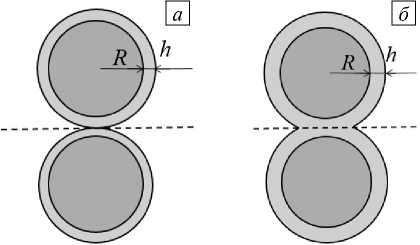
Рис. 5. Расчетная схема задачи моделирования процесса формирования микротяжа при наличии приповерхностных слоев вокруг частиц наполнителя: слои контактируют, но не пересекаются ( а ); пересечение слоев ( б )

контактирующих с поверхностью наночастиц молекул эластомера и их проскальзывание, но в данной работе расчеты проводились только при полной адгезии на границе матрицы и включений. Такое решение было связано с тем, что условия межфазного контакта (адгезия или проскальзывание) сказываются на процессе формирования микротяжа в основном количественно, тогда как в качественном отношении картины весьма похожи (см. результаты в подразделе 4.1).

Расчетная схема для изучения влияния приповерхностных слоев представлена на рисунке 5. Как и ранее, исходный зазор между частицами б0 составлял 0,4R. Исследовано два варианта: 1) слои касаются друг друга в зазоре (толщина каждого слоя h = 50/2); 2) слои в зазоре полностью перекрывают друг друга (h = 50). Случай, когда слои настолько малы, что не пересекаются, здесь не рассматривался, так как его можно интерпретировать как систему из двух более близко расположенных сфер большего диаметра.

Для описания механических свойств материала слоя также использовали неогуковый потенциал (2), только в него вместо E_m входила упругая константа E_s (начальный модуль Юнга), которая по мере удаления от поверхности частицы менялась по линейному закону в соответствии с формулой:

I E m [ 1 + C s h-x ) ,   x е [ 0; h ] ,

Es = ] V h 7 [ Em ,                  x > h,

где x — расстояние до поверхности жесткой сферы в исходном ненагруженном состоянии композитной ячейки, C_s — параметр «усиления», отвечающий за интенсивность изменения жесткости слоя (от E_m на удалении h от поверхности включения до E m (1 + C s ) на границе межфазного контакта). При расчетах C_s принимали равным 9, то есть максимальное значение жесткости материала в слое (вблизи поверхности включения) в 10 раз превышало величину жесткости материала матрицы. В случае взаимного пересечения слоев константу E_s определяли следующим образом: в ненагруженном состоянии через середину зазора ( 50/ 2) мысленно проводилась перпендикулярная межцентровой линии секущая плоскость, разделяющая зону перекрытия слоев на две симметричные части (на рисунке 5 ее след показан штриховой линией). Значения E_s в каждой из этих частей также вычислялись по формуле (3) в зависимости от удаленности до ближайшего включения. Такое допущение не противоречит физическому смыслу, если считать, что причиной повышенной жесткости слоя служат осажденные части полимерной молекулы на поверхности включения.

Процессы возникновения и развития микротяжа при наличии слоев вокруг включений отображены на рисунке 6 а - в (слои касаются друг друга, h = 5 0/ 2) и 6 г - е (пересечение слоев, h = 5 0 ). Штриховыми линиями показаны границы между внешней поверхностью слоя и матрицей. На рисунках 6 а , г представлены картины распределения прочностного критерия f в момент появления первичного повреждения матрицы ( Х = 1,38, Х = 1,70 соответственно). На рисунках 6 б , д даны аналогичные распределения на промежуточном этапе превращения уже образовавшегося микроразрыва в тяж. Рисунки 6 в , е отвечают окончательной стадии, когда микротяж полностью сформировался.

Анализ результатов проведенных расчетов показал следующее:

• 1)    С увеличением толщины слоя появление первичных микроповреждений происходит при меньших макродеформациях. В случае отсутствия слоев (то есть при h = 0, см. Рис. 4 а ) процесс разрушения

  
  
  
  
  
  
  
  
  

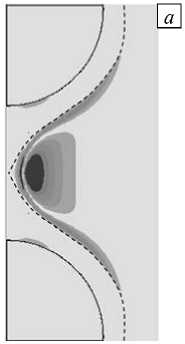
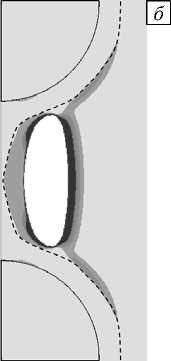
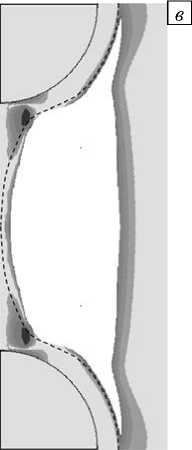
Рис. 6. Поля распределения критерия f , когда слои вокруг включений касаются друг друга ( а – в ) и перекрываются ( г – е ); возникновение первичного повреждения при Х = 1,70 ( а ) и Х = 1,38 ( г ); микротяж находится в процессе формирования, Х = 1,98 ( б ) и Х = 1,47 ( д ); микротяж полностью сформировался, Х = 2,17 ( в ) и Х = 1,87 ( е ); штриховая линия - граница между слоем и матрицей

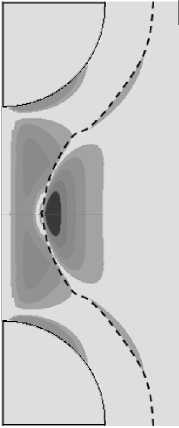
Рис. 6. Продолжение

матрицы начинается при X = 1,85 , тогда как для h =5 0/ 2 и h = 5 0 этот момент соответствует деформациям X , равным 1,70 и 1,38 (Рис. 6 а, г ). Первые микроповреждения возникают только в матрице вблизи ее границы со слоем, причем формирование тяжа на начальном этапе происходит только за счет разрушения матрицы.

• 2)    По мере увеличения внешней нагрузки в процесс разрушения включаются и приповерхностные слои (Рис. 6 б , д ), первичные микроразрывы собственно слоев начинаются сразу в двух местах на некотором удалении от полости, уже сформировавшейся вследствие разрушения матрицы. В дальнейшем происходит соединение всех полостей.

• 3)    При отсутствии слоев микротяж прорастет так, что полностью отделяется от окружающей включения матрицы (Рис. 4 в ). Если же вокруг частиц имеются слои, то этого не происходит, локальное разрушение не доходит до поверхности включения, а продолжает развиваться вдоль границы «матрица – слой» в сторону от зазора, как показано на рисунке 6 в для контактирующих слоев. На рисунке 6 е изображена ситуация в системе на момент окончательного формирования микротяжа для перекрывающихся слоев, но до того, как начнется дальнейшее прорастание локального разрушения. Оно происходит аналогично предыдущему.

• 4)    Поперечный размер образующегося тяжа пропорционален толщине приповерхностного слоя, причем большая его часть состоит из материала слоя, то есть жесткость больше, чем у матрицы.

4. Заключение

Предложен новый подход к описанию процесса развития внутренней поврежденности в дисперсно наполненных эластомерах. Учитываются такие особенности композитной структуры, как высокая концентрация напряжений в зазорах между близко расположенными включениями, наличие на поверхности частиц наполнителя эластомерных слоев с повышенной жесткостью, различные условия межфазного контакта (полная адгезия или проскальзывание на границах раздела фаз).

В основе подхода лежит гипотеза о возможности анизотропного упрочнения эластомера в процессе деформирования, согласно которой при одноосном растяжении достигается максимальная прочность по сравнению с другими видами напряженного состояния. Предложен соответствующий прочностной критерий. Расчеты показали, в этом случае локальные разрывы матрицы возникают не в промежутке между частицами (в местах наибольшей концентрации напряжений), а на некотором удалении, вокруг промежутка формируется «пустотелое кольцо» — микротяж. Таким образом, взаимосвязь между включениями не нарушается, и на макроуровне материал сохраняет свою несущую способность. Это явление может служить одним из возможных объяснений упрочнения эластомера при вводе в него жесткого дисперсного наполнителя.

Работа выполнена при финансовой поддержке РФФИ (проект № 19-08-00725_а).