Структурное моделирование взаимосвязей целей устойчивого развития регионов

Автор: Алферова Т.В., Третьякова Е.А.

Журнал: Вестник Южно-Уральского государственного университета. Серия: Экономика и менеджмент @vestnik-susu-em

Статья в выпуске: 2 т.18, 2024 года.

Бесплатный доступ

Статья посвящена установлению взаимосвязей между целями устойчивого развития (ЦУР) региона на основе структурного моделирования. Цель исследования - разработка инструмента анализа и систематизации сложных взаимодействий ЦУР регионов как основы для формирования региональной политики в области устойчивого развития. Актуальность темы обусловлена тем, что используемые для этих целей количественные методы объективны, но трудоемки и, опираясь только на измеримые показатели, могут искажать суть ЦУР. Качественные же методы учитывают больше нюансов, но субъективны. Следовательно, необходим инструмент, объединяющий сильные стороны и нивелирующий недостатки данных подходов. Таким инструментом, по нашему мнению, является структурное моделирование - подход, пока не имеющий широкого применения и поэтому требующий серьезной методической проработки, которая и составляет важную часть данного исследования. Методические основы исследования: экспертные оценки применялись для выявления наличия и направленности взаимосвязей ЦУР; методы математической статистики использовались для объективизации мнений экспертов путем выявления наиболее значимых взаимосвязей; иерархический и логический анализ - для формирования структуры взаимосвязей; метод матричного позиционирования - для выявления силы влияния и зависимости между ЦУР. Новизна исследования заключается как в синтезе данных методов, так и в полученной в результате этого структурной модели взаимосвязи ЦУР регионов. Практическая значимость авторской методики заключается в ее способности переводить сложные, субъективные и разрозненные качественные представления о взаимодействии ЦУР в измеряемый, визуальный и понятный формат для лиц, принимающих решения. К наиболее значимым выводам, полученным с помощью авторской модели взаимодействия ЦУР, также имеющим научную новизну, можно отнести установление в качестве «входов» системы взаимосвязей ЦУР 16, ЦУР 17 и ЦУР 4 как детерминант устойчивого развития региона, а в качестве «выхода» - ЦУР 11 как его результат. Это необходимо учитывать при разработке региональной политики в области устойчивого развития.

Еще

Регион, устойчивое развитие, структурное моделирование, взаимосвязь цур, влияние, зависимость, иерархия, приоритеты, программы развития

Короткий адрес: https://sciup.org/147243944

IDR: 147243944 | DOI: 10.14529/em240201

Текст научной статьи Структурное моделирование взаимосвязей целей устойчивого развития регионов

Подход к устойчивому развитию, заложенный в ЦУР, основан на идее о том, что экономическое процветание, состояние окружающей среды и социальное благополучие являются взаимосвязанными элементами, которые нельзя рассматривать отдельно друг от друга1. Данная взаимосвязь прослеживается в формулировках ООН, касающихся ЦУР, например, «устойчивый и всеохватный эко- номический рост (ЦУР 8) может способствовать прогрессу, создавать достойные рабочие места для всех и улучшать уровень жизни (ЦУР 1)» или «устойчивое потребление и производство (ЦУР 12) могут внести существенный вклад в сокращение масштабов нищеты (ЦУР 1)», или «получение образования (ЦУР 4) закладывает основу для улучшения социально-экономических условий жизни людей и играет ключевую роль в обеспечении выхода из нищеты (ЦУР 1)»2 и т. д. Многие ЦУР являются многомерными, и помимо взаимодопол- няемости, между ними могут возникать синергия и компромиссы, следовательно, выявлять взаимосвязи необходимо только на системной основе.

В научной литературе, посвященной обзору методов, подходов, предположений о взаимосвязи ЦУР, выделяют пять основных методологических подходов. В частности, А. Миола с соавт. описывают лингвистический подход (по ключевым словам), литературный подход (по взаимосвязям, установленным в научной литературе), аргумента-тивный подход (на основе экспертных оценок), количественный подход (статистический анализ базовых показателей) и моделирование [1]. К примеру, первые два подхода реализованы в работах Д. Ле Бланк и соавт., изучавших отчеты системы ООН и других международных организаций и систематизировавших материалы, касающиеся океанов, на основе списка ключевых слов [2]. Поскольку материал, полученный из отчетов, охватывал лишь часть связей, авторы провели анализ научной литературы по данной теме. Результатом стали карты взаимосвязей, существующих между задачами ЦУР 14 «Сохранение и рациональное использование океанов, морей и морских ресурсов в интересах устойчивого развития»3 и другими ЦУР [2, 3]. К. Владимирова аналогично исследовала связь между ЦУР 4 «Обеспечение всеохватного и справедливого качественного образования»4 и прочими ЦУР [4]. А. Миола с соавт. для выявления взаимосвязей, синергии и компромиссов между ЦУР также использовали комбинацию двух указанных подходов [1]. На основе анализа литературы А. Карниб осуществил картирование прямых и косвенных взаимосвязей между ЦУР [5], А. Оливейра с соавт. реализовали формальное моделирование приоритетности глобальных ЦУР [6] и т. д.

Экспертные оценки – не менее востребованный подход к установлению взаимосвязей между ЦУР. Так, Ф.Ф. Нерини с соавт. привлекали экспертов для определения взаимосвязей между ЦУР 7 «Обеспечение всеобщего доступа к недорогим, надежным, устойчивым и современным источникам энергии для всех» и целями Повестки дня 2030 в целом [7], Н. Вайц с соавт. и А. Бойтор с соавт. построили на основе экспертных оценок матрицы перекрестного воздействия ЦУР [8, 9] и т. д.

Количественный подход, основанный на статистическом анализе наборов показателей, встречается в исследованиях взаимосвязей ЦУР не менее часто, к примеру, Б. Майнали [10], Ф. Лауманн [11], Ж.-П. Клинг [12] и мн. др. используют его для выявления ковариации и корреляции между целями и задачами с последующим сетевым представлением результатов.

Моделирование – перспективный и одновременно сложный аналитический инструмент изучения взаимодействия ЦУР. С ростом интереса к моделированию и уровня сложности моделей возрастает объем научной литературы, посвященной данной тематике. В частности, К. Аллен с соавт. исследовано 80 различных моделей, проведен сравнительный анализ сильных и слабых сторон, дана оценка их общей полезности посредством многокритериального анализа [13]. Поскольку применение моделей и симуляторов обычно требует значительных ресурсов, подход чаще всего используется для решения конкретных научных и практических задач. В частности, в отечественной научной литературе, касающейся социальноэкономического развития регионов, моделирование чаще всего применяется для оценки синергии региональных программ, но без учета ЦУР (М.А. Шаталов [14], В.В. Побирченко [15], М.М. Шевырев [16], Т. Д. Омаров, Н.В. Моргунова, Д.А. Синявский [17], А.И. Ярембаш, Н.В. Кохан [18], Н.Т. Паздникова [19] и др.).

В целом изучение взаимодействий ЦУР остается относительно новой областью исследований со значительным числом пробелов в выявлении наличия и направленности взаимосвязей между ними. Качественные методы отличаются трудоемкостью и отчасти субъективностью, в то время как количественные требуют предварительного сбора и обработки статистических данных, выбора и адаптации моделей и т. д. В связи с этим поиск инструментов выявления взаимосвязей между ЦУР, объединяющего сильные стороны различных подходов, является актуальным и своевременным особенно для систем регионального уровня. Целью данной работы является выявление взаимовлияния ЦУР методом интерпретационного структурного моделирования. Новизна исследования состоит в интеграции методологий ISM-DEMATEL-MICMAC и их адаптации к решению задач идентификации и оценки взаимного влияния ЦУР с учетом регионального контекста.

Методологические подходы

Методология интерпретационного структурного моделирования (ISM), предложенная Дж. Уорфилдом [20], направлена на качественный анализ взаимосвязей между переменными путем разложения сложной системы на составляющие элементы, с последующим построением структурированной модели этой системы. ISM имеет многоуровневую структуру и способна выявлять неоднозначные зачастую интуитивные взаимосвязи, что увеличивает глубину анализа сложных систем.

В последние годы методология вызывает большой интерес у исследователей и практических специалистов в области производства, менеджмента, государственного управления и др., однако наиболее часто она используется в управлении цепочками поставок [21–25]. Интересным является опыт А. Резайян и Р. Багери, применивших ее «для построения иерархии и классификации факторов, определяющих функционирование сетей знаний» [26, с. 56]. Отметим, что в отечественных научных разработках данный подход не нашел широкого применения.

Как правило, методология ISM включает следующие этапы [21, 22, 26, 27]:

1) определение релевантных элементов, теоретически и эмпирически подтвержденных результатами, опубликованными в научноисследовательских статьях;
2) определение взаимосвязей методом парных сравнений элементов с использованием структурной матрицы взаимодействия ( structural selfinteraction matrix, SSIM );
3) формирование начальной/исходной бинарной матрицы достижимости (initial reachability matrix, IRM) для отражения направленных отношений между всеми элементами, при этом элемент равен 1, если отношения существуют, и 0 – если отношения отсутствуют. В случае если взаимосвязь устанавливается по данным научной литературы [21, 23], то вместо 1 используется соответствующее количество статей, в которых авторы указывают на данную связь;
4) проверка полученной матрицы на транзитивность (т. е. если i влияет на j, и j влияет на k, то i влияет на k. Если это условие выполняется, то транзитивность присутствует – T, если нет, то она отсутствует – 0 [21]. В результате формируется окончательная / финальная матрица достижимости (final reachability matrix, FRM) ;
5) фракционирование переменных финальной матрицы достижимости на уровни путем определения наборов элементов достижимости (самой переменной и других переменных, на которые она влияет), наборов антецедентов / предшественников (самой переменной и других переменных, влияющих на нее) и наборов пересечений (с их помощью невозможно получить факторы более высокого уровня);
6) кластеризация переменных одного уровня с целью формирования конической матрицы и орграфа путем удаления транзитивных связей (пересечений) для того, чтобы оставить в наборе только причинно-следственные цепочки;
7) преобразование орграфа в модель ISM, проверка на предмет концептуальных несоответствий, при необходимости внесение корректировок.

В адаптированной авторской методике в качестве релевантных элементов используются глобальные ЦУР ООН, а экспертами устанавливаются направленные, а не гипотетические взаимосвязи, поскольку взаимосвязь ЦУР уже заложена в самом принципе их формирования и использования в качестве ориентира устойчивого развития. Под «направленностью» здесь понимается направление связи между двумя ЦУР, если таковая существует (от i к j, от j к i, или в обоих направлениях).

Подготовительный этап предлагаемой методики заключался в формировании бланка треугольной матрицы SSIMдля 17 ЦУР в Microsoft Excel и подборе экспертов, в числе которых 6 чел. – специалисты-практики, имеющие знания и опыт работы в областях, сопряженных с ЦУР (КСО, ESG, социальные, экологические проекты и пр.) и 5 чел., привлеченных из академической среды, имеющих ученые степени кандидатов и докторов наук, область научных интересов которых связана с устойчивым развитием социально экономических систем. По нашему мнению, так будет реализовано участие стейкхолдеров академического и гражданского уровня в формировании политики устойчивого развития региона, а также обеспечено содействие локализации глобальных и национальных ЦУР до регионального уровня.

Шаг 1. Определение взаимосвязи и ее направленности между ЦУР с использованием четырех общепринятых символов [22, 26, 28]:

V – ЦУРi влияет на ЦУРj (способствует ее достижению или отдаляет от нее);
A – ЦУРj влияет на ЦУРi (способствует ее достижению или отдаляет от нее);
X – ЦУРi и ЦУРj взаимозависимы;

O – между ЦУРi и ЦУРj не существует связи.

Указанные символы выставлялись каждым экспертом на основе соотнесения каждой ЦУР с другими ЦУР попарно по строкам и столбцам на основе собственных знаний и практического опыта. Пример матрицы, заполненной нами на основе гипотезы о взаимосвязях ЦУР, представлен в табл. 1. Гипотеза формулировалась на основе характеристики глобальных ЦУР, представленной на официальном сайте ООН5. Однако не все формулировки указывают на прямую взаимосвязь между целями, кроме того, глобальные ЦУР и соответствующие им национальные ЦУР не учитывают региональный (субнациональный) контекст, как того требует Дорожная карта локализации ЦУР6, а ориентированы на решение глобальных и/или национальных проблем в целом (по принципу «сверху вниз»). При этом акцент делается на важности одновременного достижения всех ЦУР без установления приоритетов, а следовательно, не учитывается синергия и компромиссы между ними. Это, по нашему мнению, является серьезным препятствием для разработки и реализации региональной политики в области устойчивого развития. В связи с

Далее были сформированы исходные бинарные матрицы достижимости (IRM). Для этого символы из ячеек матрицы SSIM были сконвертированы в бинарные значения 0 и 1 на основе правил, приведенных в табл. 2.

Таблица 2 Правила конвертации [26, с. 62]

Значение ячейки (i, j) в SSIM	Значение ячейки (i, j) в IRM	Значение ячейки (j,i) в IRM
V	1	0
A	0	1
X	1	1
O	0	0

Шаги 2–4 были реализованы с использованием методики DEMATEL (Decision Making Trialand Evaluation Laboratory), разработанной Женевским институтом Battelle для оценки силы влияния между различными элементами в сложной среде [29]. Благодаря простоте механизма определения прямых и косвенных связей DEMATEL получила ши- рокое распространение в научных исследованиях [24, 30, 31, 32 и др.].

Шаг 2. Построение матрицы прямых связей (Х) путем объединения мнений экспертов, где xij выражает степень, в которой xi влияет на xj и наоборот, значение любого элемента на диагонали равно 0 [24, 30]:

Х =

0 х12 ... х1п х21 0 ... х2п хп1 хп2... 0

Шаг 3. Формирование нормализованной матрицы ( N ), где в качестве нормализованного базиса используется значение максимальной суммы вектора строки матрицы прямых связей Х:

N =

max ⁿ x

0 < i < n^J = 1 j^J

Шаг 4. Формирование полной или общей матрицы прямых и косвенных связей (T)по следующему уравнению:

T = lim( N + N 2+--- + Nk) = N (I - N )-1, (3) k —>® где I – единичная матрица.

Шаг 5. Выявление наиболее значимых причинно-следственных связей по методике, предложенной Р. Лентом [30, 33], путем определения порогового значения. Следует отметить, что на установку порогового значения влияют сложность проблемы и расхождения во мнениях экспертов. Исследователи используют различные методы установки порогового значения. Метод, предложенный Р. Лентом, основывается на предположении о разреженности эффектов, поэтому для оценки стандартных отклонений эффектов используется цензурирование и псевдостандартные ошибки, что позволяет получить статистику, аналогичную t-тестам. Пороговые значения, полученные с помо- щью данного метода, затем используются для определения значимости эффекта [30, с. 7]:

median

So = 1,5 x---------

1 < k < m

A в к

где S0 – начальное значение.

Медиана выбирается из матрицы пря-мых/косвенных связей T

PSE = 1,5 x

median

A в к < 2.5 S о

A вк

где PSE – псевдостандартная ошибка, рассчитанная на основе медианы, полученной из коэффициентов абсолютной регрессии меньше 2,5S0.

ME = ^ a m x PSE , (6) 2;3

где МЕ – предел ошибки для различных коэффициентов регрессии.

Шаг 6. Формирование финальной матрицы достижимости (final reachability matrix, FRM) по методологии ISM [21, 22, 25–27].

Шаг 7. Разделение ЦУР на четыре кластера (автономные, зависимые, связующие, независимые) на основе подхода MICMAC (Matrice Impacts Croisеs Multiplication Appliquеeаun Classement) [21–23, 26, 27, 34]. Положение ЦУР отображается в двухмерной системе координат на основе значений степени зависимости и силы влияния, представленных на горизонтальной и вертикальной осях соответственно. Диапазон значений составляет от 1 до их общего количества, а оси делятся на две части в средних точках, в результате чего образуются четыре квадранта, пронумерованные против часовой стрелки [27].

Шаг 8. Построение конической матрицы (Conical Matrix, CM) и орграфа зависимости ЦУР. CM представляет собой упорядоченную по строкам и столбцам FRM на основе рангов или уровней переменных, которые записываются в конце строки и столбца CM [27]. Данная матрица способствует построению орграфа – визуального отображения направленной иерархической структуры ЦУР.

Шаг 9. Проверка орграфа на наличие концептуальных несоответствий и построение итоговой модели взаимосвязи ЦУР региона.

Результаты

Данное исследование направлено на выявление взаимозависимых структурных отношений между ЦУР регионов и формирование на этой основе модели, простой и удобной для специалистов-практиков при определении приоритетов региональной политики в области устойчивого развития.

Шаг 1. Процедура экспертной оценки включала анализ отношений и типа контекстуальной связи между любыми двумя ЦУР (i и j) («зависит от», «влияет на», «влияют друг на друга», «не взаимодействуют»). Каждый из 11 экспертов индивидуально заполнил матрицу SSIM (см. табл. 1), которая затем была конвертирована в бинарную матрицу IRM (см. табл. 2). Дальнейшая обработка полученных результатов осуществлялась с использованием методики DEMATEL.

Шаг 2. Направленные связи между любой парой ЦУР (i и j) записывались в матрицу прямых связей (Х) как количество мнений экспертов, считающих, что такое взаимодействие существует, в противном случае записывался ноль. Этот процесс проводился как для i на j, так и наоборот, всего 17×17 элементов матрицы. Значение любого элемента на диагонали равно 0. Количественное выражение силы влияния (DRV) и степени зависимости (DEP) каждой ЦУР были отражены в виде суммы значений ячеек в последнем столбце и последней строке таблицы соответственно. Выявленные прямые взаимосвязи между ЦУР представлены в табл. 3.

Полученная таблица одновременно демонстрирует как единодушие экспертов по ряду ЦУР, так и отличие их мнений в ряде случаев, что связано со сложностью решаемой задачи, на которую указывают многие исследователи, занимающиеся аналогичной проблемой. В частности, Д. Ле Бланк упоминает о критике картирования связей, которая заключается в том, что «в таблицах часто «все связано со всем» и поэтому бесполезно для принятия политических решений» [2, с. 26]. Исходя из этого, необходимо учитывать только статистически значимые эффекты, оказывающие влияние на переменные отклика. Для этого следует реализовать шаги 3–5.

Шаг 3. Нормализация матрицы прямых связей в соответствии с уравнением (2). В качестве нормализованного базиса использовалась сумма строки ЦУР 4, имеющая максимальное значение (N = 1/125). Нормализованная матрица прямых связей (N) представлена в табл. 4.

Шаг 4. Матрица прямых и косвенных связей T была получена с помощью единичной матрицы I в соответствии с уравнением (3). Единичная матрица используется в данном подходе в отличие от традиционного подхода к интегрированию, где матрица общих отношений T не учитывает влияние фактора на себя. Матрица Т представлена в табл. 5.

Шаг 5. Определение наиболее очевидных причинно-следственных связей в соответствии с их пороговым значением производилось по уравнению (4). S0 = 1,5 ×0,0712 = 0,1068, где медиана (0,0712) была выбрана из матрицы T.

После удаления в матрице T значений, которые оказались больше или равны 2,5S0, было определено новое значение медианы и получено пороговое значение PSE = 0,1048 по уравнению (5). Уровень эффекта ниже порогового значения рассматривался нами как связь, не являющаяся причинно-следственной. Далее была определена матрица связей со значимым эффектом (табл. 6), что позволило объективизировать экспертные оценки и сделать результаты более информативными для лиц, принимающих решения (шаги 6–8).

Шаг 6. Матрица значимых эффектов была преобразована в матрицу 0–1, образовав финальную матрицу достижимости (FRM) (табл. 7). Кроме того, сумма строк и столбцов, характеризующих силу влияния и степень зависимости ЦУР, образовали двухмерную систему координат (рис. 1).

Шаг 7. Распределение ЦУР на четыре кластера (автономные, зависимые, связующие, независимые) было проведено на основе анализа MICMAC. Первый кластер включает «автономные» ЦУР, обладающие как слабым влиянием, так и слабой зависимостью. Они условно изолированы от системы, практически не имея связей с ней (ЦУР 5 – обеспечение гендерного равенства). Второй кластер состоит из «зависимых» ЦУР, имеющих сильную зависимость и слабое влияние на другие ЦУР (ЦУР 2, ЦУР 3, ЦУР 11 и др.). ЦУР третьего кластера, имеющие сильную зависимость и такое же сильное влияние на другие ЦУР, называют «связующими» (ЦУР 1, ЦУР 8, ЦУР 7, ЦУР 12). Их особенностью является то, что любое воздействие на них будет отражаться на других ЦУР. Четвертый кластер состоит из «независимых» ЦУР, имеющих сильное влияние на другие ЦУР при слабой зависимости от них (ЦУР 17, ЦУР 16, ЦУР 9, ЦУР 4) (см. рис. 1).

Отражая позиции ЦУР в системе координат влияние/зависимость, диаграмма MICMAC не дает представление о структуре взаимосвязей, для этого предназначена коническая матрица, применяемая в методологии ISM (табл. 8).

Шаг 8. Наборы ЦУР, представленные в конической матрице, были выведены из матрицы FRM. Для каждой из них набор достижимости состоял из самой ЦУР и всех ЦУР, на которые она влияет, а набор предшественников состоял из нее самой и всех ЦУР, влияющих на нее. Переменным, имеющим одинаковые наборы достижимости и пересечений, присваивался высший ранг, и они удалялись для следующей итерации, процесс повторялся до тех пор, пока все переменные не были ранжированы [21, 25, 27] (табл. 9).

co я 3 S

ю я 1

>S я ГС ш о

ГС а с

S о. 1я 2

ОО

СП

Г)

СП

СП 4©

сч ОО

04 04

сч 4©

сч

<п

•п

о тГ

4© О

сч

X ^

сч

—

ОО

г-

—

Г-

СП

сП

4©

гл

о\

сч

•п

СП

сч

СП

МП

Он ^

сч

ОО

сч

г-

а-

сч

ОО

сч

ОО

сч

г-

—

сч

•п

сч

Г-

г-

ОО

ш 00

СЧ

ГП

—

СП

—

гч

4©

Он

О'

—

ОО

О'

СП

сч

'Г

СП

сч

4©

ОО

сч

■^

СП

Г'

О' Он

сч

гч

ГП

СП

—

ОО

4©

ОО

•п

сч

—

ОО

ГП

г-

СП 04.

—

н-

сч

СП

тг

—

сч

Г-

сч

ЧО CL

тГ

’t

гч

4©

г-

СП

ОО

■п

'П^-

СП

in ей

сч

—

СЧ

ОО

■*

С-

СЧ

си

«п

сч

ТГ

СП

4©

сю

pH Д

ОО

г-

СЧ

НГ

4©

СП

4©

СП

тГ

■л

СП

сГ

ТГ

«1

Он

—

ОО

сч

'Lt

ОО

—

сч

СЧ

ОО

Он

гч си

—

=Г

со

04 CL

сч

Он д

Cl.

а.

4©

Он

С-

0. а

S’ S X

в га Д

О 40

о ОО о о_ о'

о о

ОО

о о*

о о о о_ о

О о о О' о"

о ОО о о о"

40 о о

о 40 ш 0^ o'

о 00 о о о"

о о о О' o'"

о 40 ш о^ о”

сч о^ о"

сч о_гo'

о ’Т сч о

о CD

О o'

о о о °, o'

СЧ CD

о 00 о о о"

о о о О' о

о 04

О^ о

о 40

о о

о о О о o'

о о о О_го”

о о

О' о

С-4 О^ o'

о С]

о о"

о о о О' о"

о 40

о_ о”

о о о О_гo'

о ос О О_го

о 00 о о

о о о О' о"

о о

О' o'

О 40

о о о о о"

о о о О" о"

40 О' о"

о о о О' о

о С4

О' o'"

О 40

О" о”

о о

о.

■40 о"

о 40

о_ о"

о о о О' о

о 00 ОО о_ о"

о ос ОО О_го

о сч

о о

о о о CD_ro'

о 40

о o'

о 40

°, о"

-f x

CD 40

CD o'

о о о о о"

о о о О_го"

о Tt 40 о_ о'

о О о О' о

о Г4 СП о о'

о 40

О_го"

о о

О'

40 О' o'

о 40

о. о"

о о о О' о'

о ОО 00 О' о"

о 00 00 о o'

о о о о о

о 40 О' cd"

о 40

О' о"

о in О' о'

О QO О О o'

о о о о o'

о о о О' о'

о ОО 00 о, o'

о 40

о о'

о о со о o'

о о

о”

о ОО ОО о^ o'

о 40

о o'

о о о о o'

о сч

0^ о”

о о о

о"

о 40 МП О' о”

о 40

о^ o'

о о ОО О^ о"

40 о^ о”

сч

о о 00 о. o'

п О' о*

о 00 о О' о"

о о 00 о, о

о о о о

О' о"

о о 00 О_го”

о о

о ОС 00 о^ о'

о 00 о О' o'"

о о о О' о"

о о о

о"

о о

о^ о"

о 00 о О_го"

о 00 о CD_ro'

о 00

40 О' o'

о о 00 о^ o'

о о 00 О' о"

о 04

О' о'

о 00 о о

о СЧ

О' о"

о 40 0, О^Г

о С4

О' о

о ОО ОО О' o'

о о

о o'"

о о о О' о"

о сч

О_го"

сч О" o'

о 4©

о о

о 40

о о"

40 О' о"

о o'

5 о

= &

о' o'

о г-1 о"

о 40

о о”

о 00

о, о”

40 О' о

04 о o'

о о 00 О_гО^Г

о 40 ш О' о

о 40

о о

о о о О' о'

о с-4

^Ое о'

С-1 О' о"

о 00 о О' o'

о о о О' о

о о о ч О^Г

о о 00 о^ о"

о 40 in о o'

I O'

о о

о о"

о 40

о o'

о о

о^

О^Г

о ОО ОО о о”

о тГ п о

о С] СП о o'

о 00

О' o'

о СЧ

о о

о о о о о'

о С4 СП О о'

о о

о o'

СЧ о о"

о 00 о О o'

о о о о

о о о о o'

40 о о"

q 00

о о

о 40

о о"

о ОО

о"

о ОО ОО о о"

о Г) гл о

о СЧ сП о о*

о о ОО О' о"

о о о о о”

о o'

40 О o'

40 о o'

о о

о ~г сч о о"

о ОО о о о"

о ОО о о o'

о о ОО о о"

о 40 in о о'

—

о о ОО о o'

о о о о

о о о о^ о"

о o'

о 40

о о

о о 00 о

о о о О_гo'

СЧ о о”

о с-1 СП о о"

о ОО о о о'

о 00

—

о"

ОО

О o'

о о

о o'

о 40

о о"

о 40

о о"

о о ОО о o'

о 40 in о о"

о СЧ

о СЧ сП о^ o'

О_го”

о^ o'

о о

о o'

о о о о o'

о 4© un О' о"

о ОО ^ о o'

о 40 in о^ o'

С] о^ о"

40 о o'

о о ОО о^ o'

о о

о о'

о сч 8 o'

сч CD o'

ОО

о^ o'

о о

о о"

о 40

о 00

о o'

о 40

40 О' o'

о о о О' o'

о о о о o'

о о о О' o'

о о

о сч

О_гo'

о 40 ш о^ о"

о 40

О' o'

о о о О' o'

о о о О' о"

о о о о

о о о О_го"

о о ОО о o'

о о ОО

О' о"

о о

о"

о 40

О' o'

ОО

О'

о о о о^ о'

о о

о ОО о о o’

о 04 СП о^ о'

СЧ о^ о

о п

о o'

о 00

о о

о с-1 СП о o'

о о о О' о'

о о о о,' о"

о о о °C о

о о о CD

о сч

о o'

о о 00 о

40 о

о о о о. о'

о о

о о'

о СЧ

о о

40 о о'

о 40 If) о_ CD

о о ОО о о

о 40 ш О' o'

о С1 СП о

ОО

о о

о*

о о

о о ОО О' о

о ОО

Q o'

о 00

ОО о o'

СЧ

о ОО 00 о о'

о о о о o'

о сч сп о о'

о ОО

о о

о ОО о о o'

о о

о о'

С 1

О'

о СЧ

о о

ОС

о o’

С1 о'

о С4 СП О' o'

о о

о о"

С 1 о^ o'

о ОО ОО о о

о сч СП о

о сч

о o'

о о о о о'

о 00 о О' o'"

о ^ 40 О_го'

СЧ

о^ о'

о тГ С-4 О' о'

о 00

о^ о'

о 40

О_го'

о о

О' о"

о Г4

о o'

о СЧ СП О' о"

о о

О'

о 40 О' о"

о 0© о О_го"

о о

о o'

о"

о 00

О' о'

о 00

О' o'

Ви

сч

СП X

а.

си в

ОО X &

04 X &

си в

СЧ

X в

си в

’Л’

X в

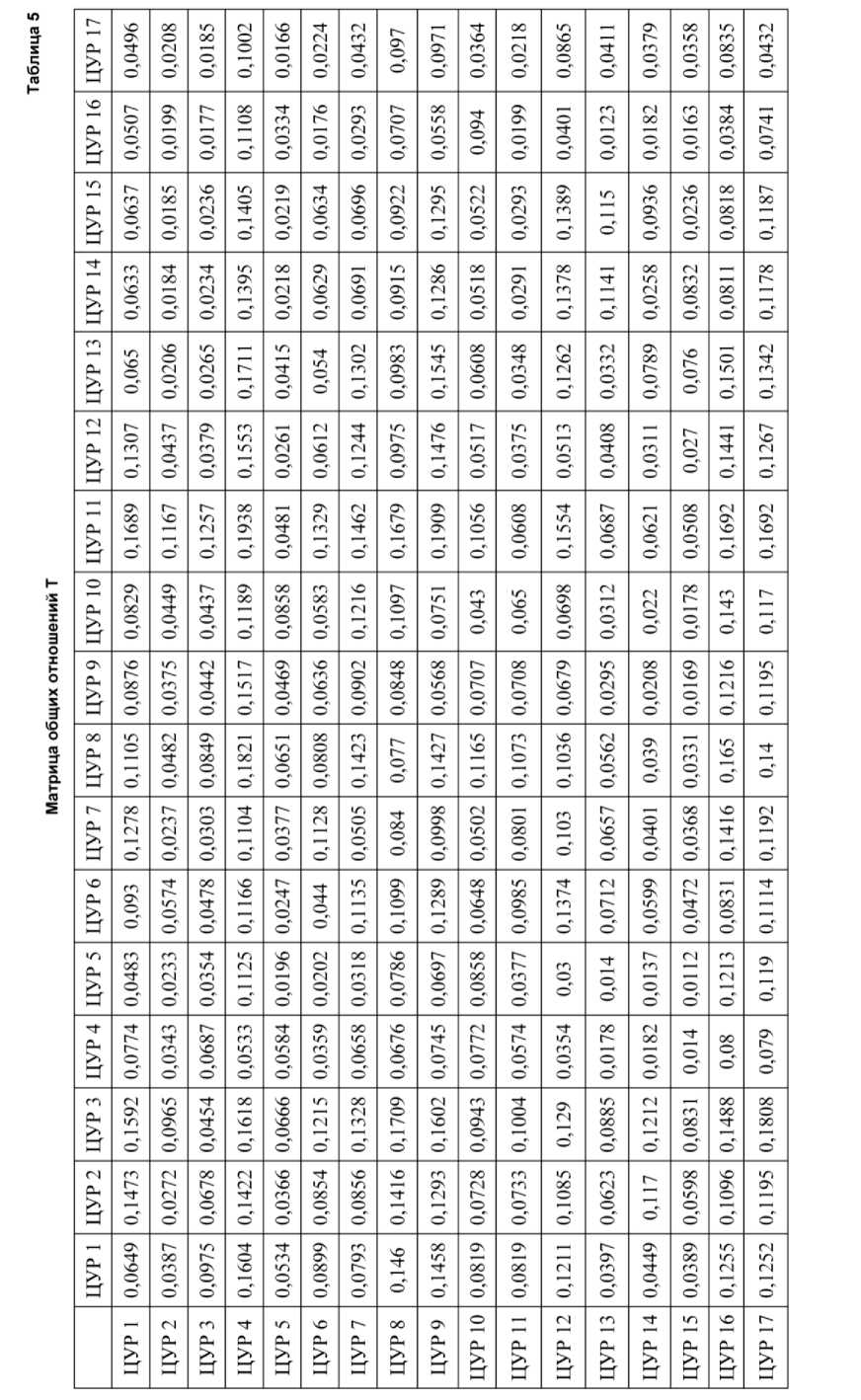
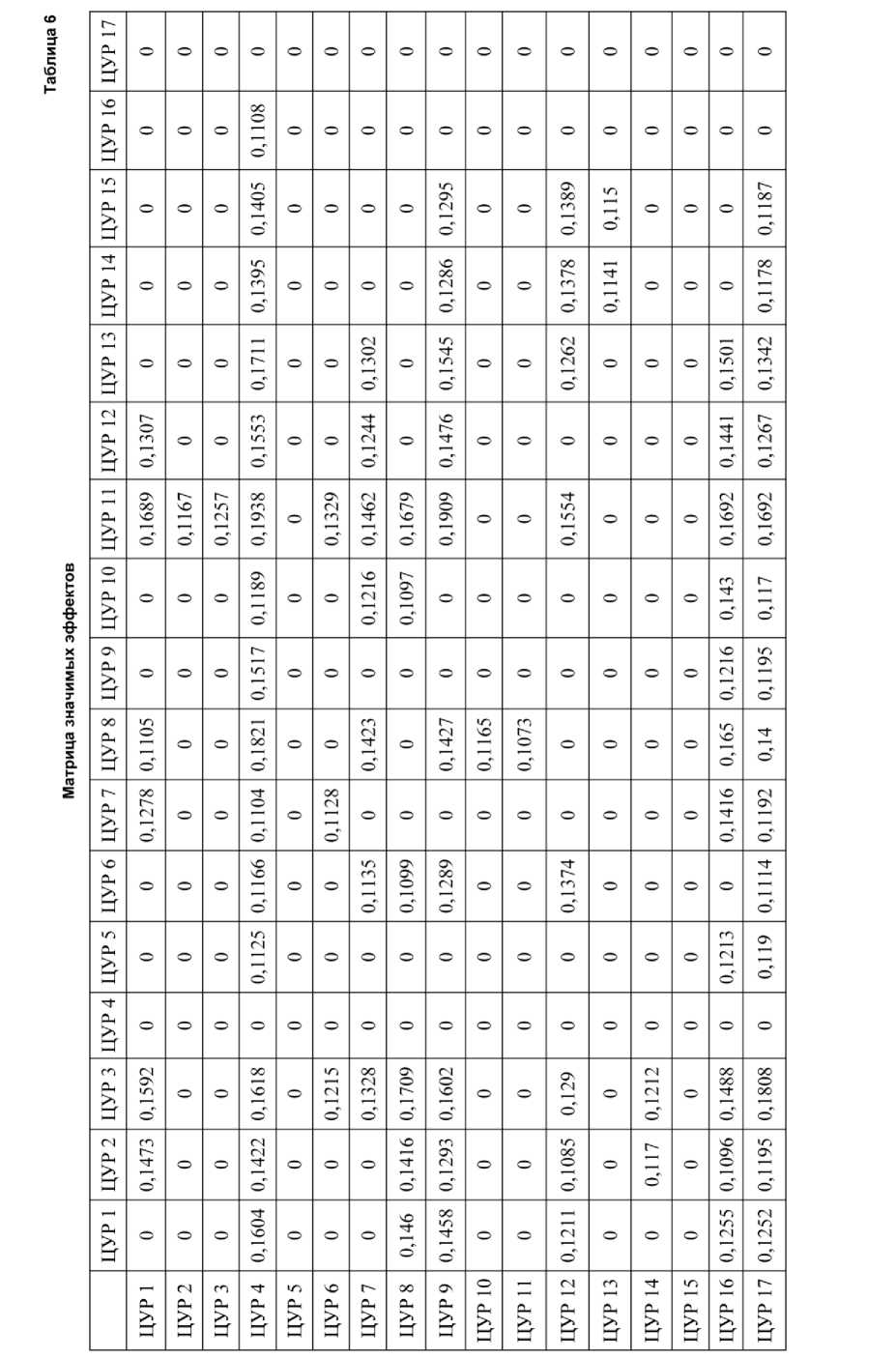
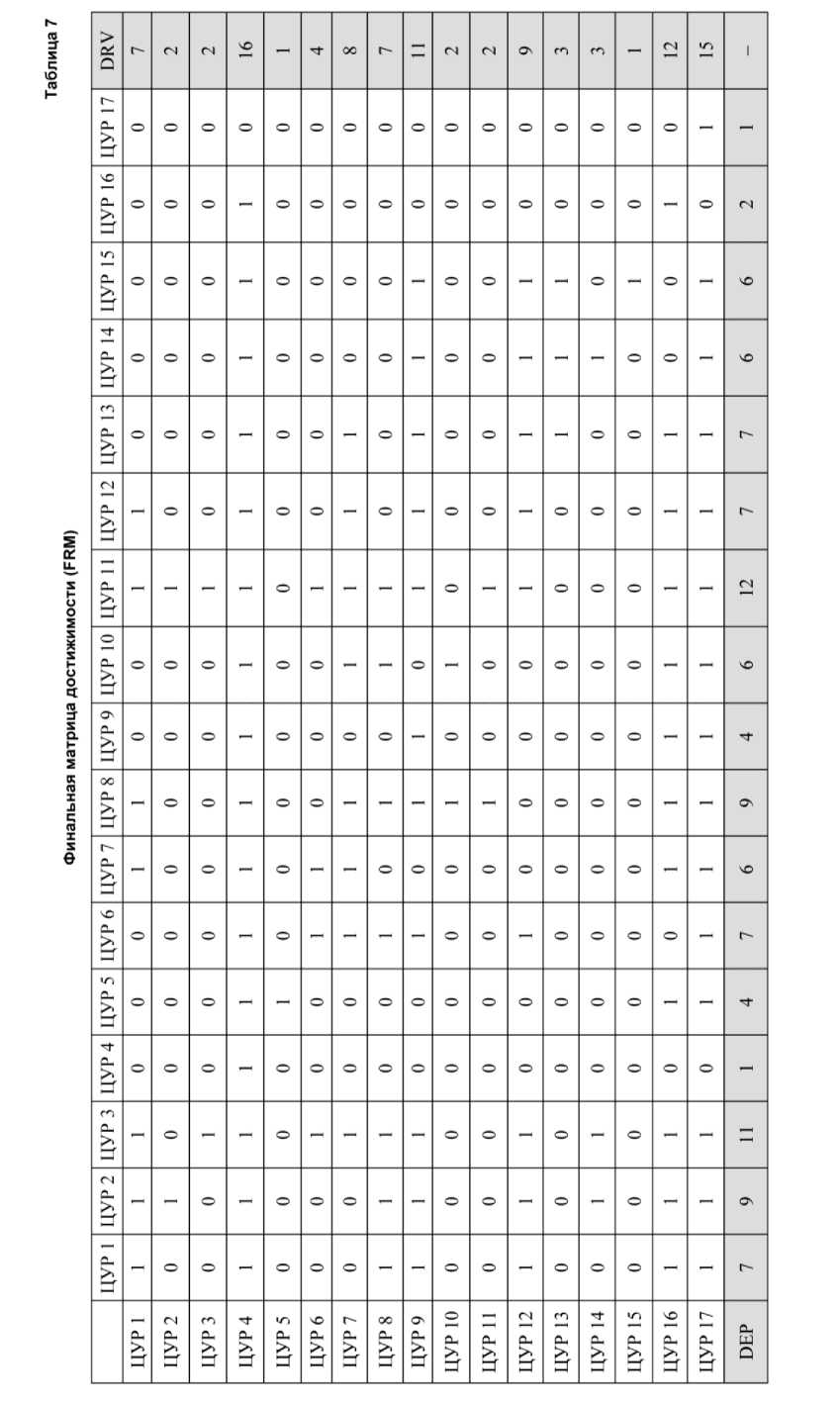
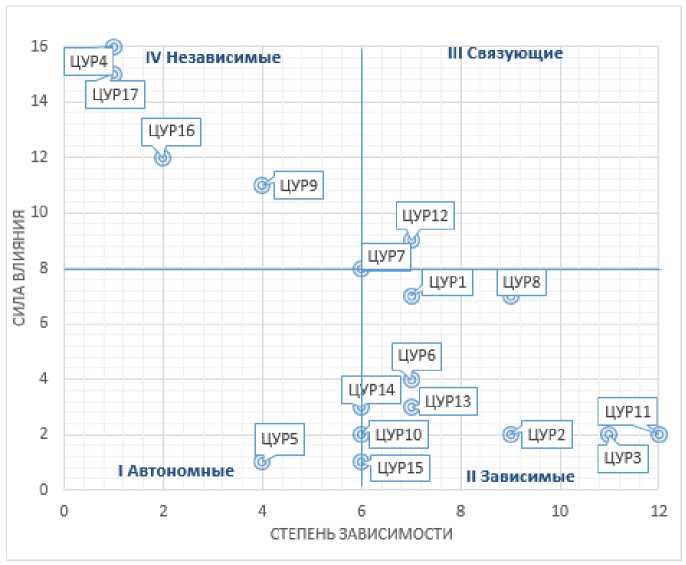
Рис. 1. Диаграмма MICMAC силы влияния и степени зависимости ЦУР на уровне регионов

ЦУР 1. Ликвидация нищеты.

ЦУР 2. Ликвидация голода.

ЦУР 3. Хорошее здоровье и благополучие для всех.

ЦУР 4. Качественное образование.

ЦУР 5. Гендерное равенство.

ЦУР 6. Чистая вода и санитария.

ЦУР 7. Недорогостоящая и чистая энергия.

ЦУР 8. Достойная работа и экономический рост.

ЦУР 9. Индустриализация, инновации и инфраструктура.

ЦУР. 10. Уменьшение всех видов неравенства.

ЦУР 11. Устойчивые города и населенные пункты

ЦУР 12. Ответственное потребление и производство.

ЦУР 13. Борьба с изменением климата.

ЦУР 14. Сохранение морских экосистем.

ЦУР 15. Сохранение экосистем суши.

ЦУР 16. Мир, правосудие и эффективные институты.

ЦУР 17. Партнерство в интересах устойчивого развития

Шаг 9. В результате фракционирования получено девять уровней направленных взаимосвязей, которые после проверки на наличие концептуальных несоответствий были преобразованы в орграф взаимосвязей ЦУР (рис. 2), а затем в итоговую модель ISM. Указанные несоответствия могут возникать в результате математических вычислений, реализованных на предыдущих этапах. Возникновение подобных логических отклонений относят к недостатку структурного моделирования [24]. Исходя из этого, модель рекомендуется корректировать путем обсуждения орграфа с экспертами.

Модель, представленная на рис. 3, является синтезом результатов анализа MICMAC, иерархического и логического анализа. Данная модель содержит незначительные корректировки, так как орграф показал достаточно точные причинноследственные цепи взаимного влияния ЦУР. Все ЦУР в итоговой модели для удобства восприятия условно были разделены нами на четыре группы: ключевые (входные) ЦУР (не зависят от других ЦУР), узловые (являются следствием ключевых ЦУР, при этом влияют на большинство других

ЦУР), результирующие (число влияющих на них ЦУР значительно больше числа зависящих от них ЦУР), зависимые (практически полностью зависят от реализации других ЦУР и влияют только на выход сети (ЦУР 11)). Исключение составляет ЦУР 1, которая в иерархии взаимосвязей находится на уровне узловых ЦУР, но с точки зрения силы влияния не может считаться таковой.

Итоговая модель взаимосвязей ЦУР, имеющая научную новизну, удобна для использования специалистами-практиками в определении приоритетов при разработке политики устойчивого развития региона. Так, ЦУР 16, ЦУР 17, ЦУР 4 можно рассматривать в качестве «входа» в систему взаимосвязей ЦУР, которые в совокупности с ЦУР 9 являются детерминирующими устойчивое развитие регионов. Исходя из этого, формирование региональной политики необходимо начинать с создания эффективных, подотчетных и транспарентных учреждений регионального управления (ЦУР 16), укрепления средств партнерства в области устойчивого развития (ЦУР 17) и обеспечения качественного образования (ЦУР 4), в т. ч.

Таблица 8

Коническая матрица достижимости

ЦУР	Набор достижимости	Набор предшественников / антецедентов	Набор пересечений
5	5	4, 5, 16, 17	5
15	15	4, 9, 12, 13, 15, 17	15
11	8, 11	1, 2, 3, 4, 6, 7, 8, 9, 11, 12, 16, 17	8, 11
10	8, 10	4, 7, 8, 10, 16, 17	8, 10
3	3, 11	1, 3, 4, 6, 7, 8, 9, 12, 14, 16, 17	3
2	2, 11	1, 2, 4, 8, 9, 12, 14, 16, 17	2
13	13, 14, 15	4, 7, 9, 12, 13, 16, 17	13
14	2, 3, 14	4, 9, 12, 13, 14, 17	14
6	3, 6, 7, 11	4, 6, 7, 8, 9, 12, 17	6, 7
1	1, 2, 3, 7, 8, 11, 12	1, 4, 8, 9, 12, 16, 17	1, 8, 12
8	1, 2, 3, 6, 8, 10, 11	1, 4, 7, 8, 9, 10, 11, 16, 17	1, 8, 11
7	3, 6, 7, 8, 10, 11, 12, 13	1, 4, 6, 7, 16, 17	6, 7
12	1, 2, 3, 6, 11, 12, 13, 14, 15	1, 4, 7, 9, 12, 16, 17	1, 12
9	1, 2, 3, 6, 8, 9, 11, 12, 13, 14, 15	4, 9, 16, 17	9
16	1, 2, 3, 5, 7, 8, 9, 10, 11, 12, 13, 16	16	16
17	1, 2, 3, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 17	17	17
4	1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16	4	4

Таблица 9

Иерархический анализ взаимосвязей ISM

ЦУР	Набор достижимости (R)	Набор предшественников / антецедентов (A)	Набор пересечений (I)	Уровень
5	5	4, 5, 16, 17	5	I
15	15	4, 9, 12, 13, 15, 17	15	I
11	8, 11	1, 2, 3, 4, 6, 7, 8, 9, 11, 12, 16, 17	8, 11	I
10	8, 10	4, 7, 8, 10, 16, 17	8, 10	I

3	3	1, 3, 4, 6, 7, 8, 9, 12, 14, 16, 17	3	II
2	2	1, 2, 4, 8, 9, 12, 14, 16, 17	2	II

14	14	4, 9, 12, 13, 14, 17	14	III
6	6, 7	4, 6, 7, 8, 9, 12, 17	6, 7	III

13	13	4, 7, 9, 12, 13, 16, 17	13	IV
8	1, 8	1, 4, 7, 8, 9, 16, 17	1, 8	IV

12	1, 12	1, 4, 7, 9, 12, 16, 17	1, 12	V

7	7	1, 4, 7, 16, 17	7	VI

1	1	1, 4, 9, 16, 17	1	VII

9	9	4, 9, 16, 17	9	VIII

16	16	16	16	IХ
17	17	17	17	IХ
4	4	4	4	IХ

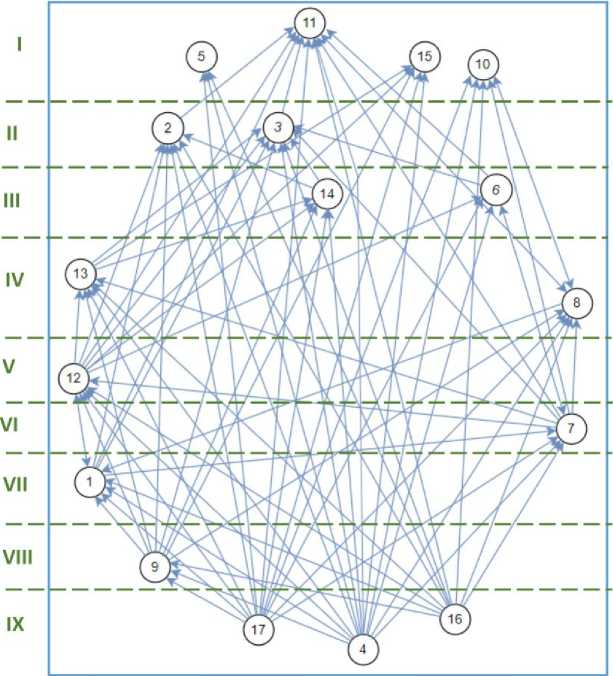
Рис. 2. Орграф взаимосвязей ЦУР на региональном уровне

управленческих кадров. Далее необходимо сосредоточить внимание на создании гибкой инфраструктуры и содействии индустриализации и инновациям (ЦУР 9), что приведет к активной разработке и внедрению устойчивых моделей производства и потребления (ЦУР 12), что в совокупности с доступом к устойчивому и современному энергоснабжению (ЦУР 7) будет содействовать устойчивому экономическому росту, полной и производительной занятости и достойной работе для всех (ЦУР 8), что поможет покончить с нищетой во всех ее формах (ЦУР 1), внесет вклад в ликвидацию голода (ЦУР 2) и обеспечит доступ к медицине (ЦУР 3). Аналогично, опираясь на эти же «входы», можно проследить все причинно-следственные цепи взаимосвязей всех ЦУР, которые благодаря данной модели стали понятными и прозрачными для стейкхолдеров. Важно, что модель демонстрирует не только иерархию взаимосвязей ЦУР, но и силу влияния и зависимости между ними. Исходя из этого, можно разрабатывать региональные программы устойчивого развития с учетом синергических эффектов и компромиссов, что позволит оптимизировать ресурсы и достичь планируемых результатов в намеченные сроки с меньшими затратами. Кроме того, это поможет расставить приоритеты в распределении ресурсов для достижения конкретных ЦУР, имеющих ключевое значение для развития конкретных регионов.

Также важно отметить, что «выходом» в данной системе причинно-следственных связей является ЦУР 11 «формирование открытых, безопасных, жизнестойких и устойчивых городов и населенных пунктов». Это практически единственная ЦУР, имеющая конкретный региональный контекст, поэтому важно, что именно ее достижение станет результатом последовательного достижения всех ЦУР, путем реализации региональных программ устойчивого развития. Достижение же ЦУР регионов приведет к достижению национальных ЦУР, делая этот процесс более прозрачным, понятным и управляемым для лиц, принимающих решения.

Выводы

Цель исследования заключалась в выявлении взаимовлияния ЦУР регионов методом интерпретационного структурного моделирования на основе синтеза методологий ISM – DEMATEL – MICMAC с последующим формированием модели взаимодействия, простой и понятной для использования в практической деятельности. В частности, методология ISM позволила перевести взаимосвязи отдельных ЦУР в организованный формат, метод DEMATEL способствовал отбору толь-

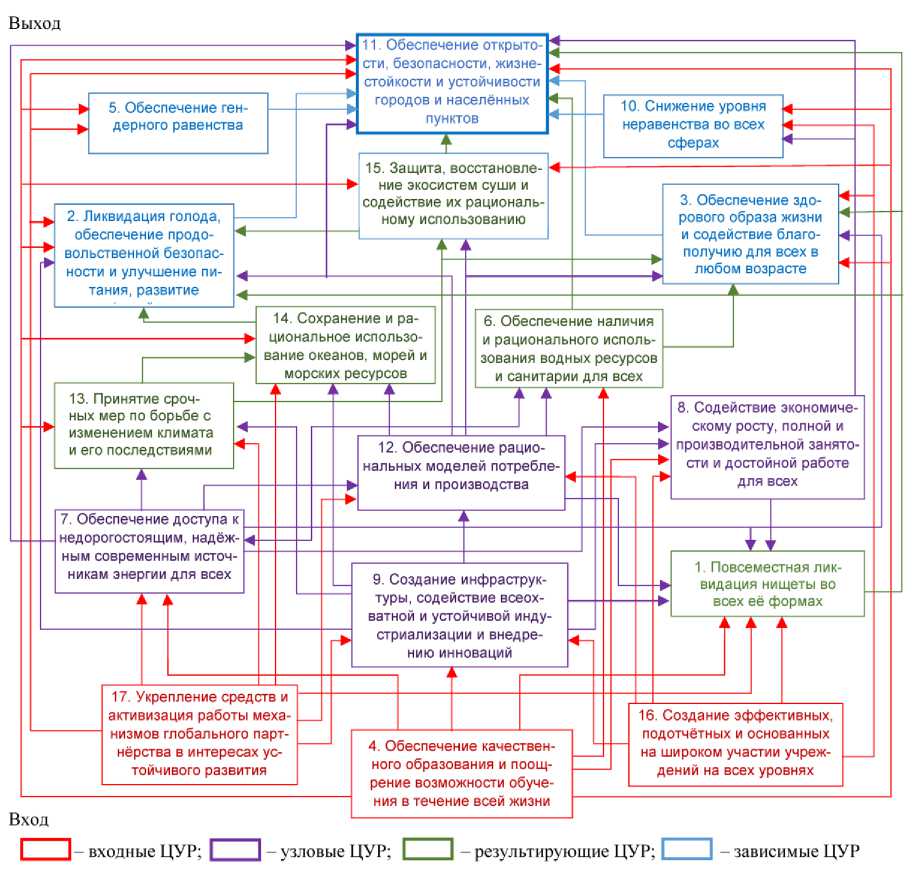
Рис. 3. Итоговая модель взаимосвязей ЦУР региона

ко статистически значимых эффектов, а метод анализа MICMAC послужил инструментом для определения силы и направленности взаимосвязей между ЦУР.

На первом этапе эксперты определяли взаимосвязи ЦУР регионов методом парных сравнений с применением структурной матрицы взаимодействия с дальнейшим ее трансформированием в бинарную матрицу достижимости.

Объединение мнений экспертов позволило построить матрицу прямых связей с ее последующей нормализацией и формированием матрицы прямых и косвенных связей. Это дало возможность выявить наиболее значимые причинноследственные связи. На их основе была построена финальная матрица достижимости. С ее помощью было проведено распределение ЦУР на четыре кластера. В первый кластер вошла ЦУР 5, являясь автономной, второй кластер зависимых ЦУР попа- ли ЦУР 2, ЦУР 3, ЦУР 6, ЦУР 10, ЦУР 11, ЦУР 13, ЦУР 14, ЦУР 15, ЦУР 1 и ЦУР 8. Третий кластер связующих ЦУР составили ЦУР 7, ЦУР 12. В четвертый кластер независимых ЦУР вошли ЦУР 4, ЦУР 9, ЦУР 16 и ЦУР 17.

Далее было реализовано фракционирование ЦУР на девять уровней путем сравнения наборов достижимости и наборов пересечений. Полученный результат показал не только положение ЦУР относительно друг друга, но и последовательность взаимосвязей между ними.

Вся совокупность множества причинноследственных связей была отражена в финальной модели взаимосвязей, включающей входные ЦУР (ЦУР 4, ЦУР 16, ЦУР 17). Именно они являются определяющими в цепи причинно-следственных взаимосвязей ЦУР или «входом» системы. Узловые (ЦУР 9, ЦУР 8, ЦУР 12, ЦУР 7), их достижение является необходимым как для достижения всех остальных ЦУР. Результирующие (ЦУР 6, ЦУР 13, ЦУР 14, ЦУР 15) и зависимые (ЦУР 5, ЦУР 2, ЦУР 3, ЦУР 10). Достижение всех ЦУР приведет в конечном итоге к формированию открытых, безопасных, жизнестойких и устойчивых регионов, что является «выходом» системы (ЦУР 11).

Полученная модель поможет лицам, принимающим решения, определить приоритеты при разработке политики устойчивого развития регионов.

Данное исследование восполняет пробел в научных разработках, касающихся как изучения взаимосвязи ЦУР регионов, так и структурного моделирования, поскольку данная проблематика пока достаточно слабо представлена в отечественной научной литературе.

Список литературы Структурное моделирование взаимосвязей целей устойчивого развития регионов

Miola A., Borchardt S., Neher F., Buscaglia D. Interlinkages and policy coherence for the Sustainable Development Goals implementation: An operational method to identify trade-offs and co-benefits in a systemic way, EUR 29646 EN, Publications Office of the European Union, Luxembourg. 2019. ISBN 978-92-79-995569. DOI: 10.2760/472928. JRC115163
Le Blanc D., Freire C., Vierros M. Mapping the linkages between oceans and other Sustainable Development Goals: A preliminary exploration. Department of Economic & Social Affairs. DESAWorkingPaper.2017. No. 149. ST/ESA/2017/DWP/149.
Le Blanc D. Towards integration at last? The sustainable development goals as a network of targets. Department of Economic & Social Affairs. DESA Working Paper. 2015. No. 141. ST/ESA/2015/DWP/141.
Vladimirova K., Le Blancb D. How well are the links between education and other sustainable development goals covered in UN flagship reports? A contribution to the study of the science-policy interface on education in the UN system. Department of Economic & Social Affairs. DESA Working Paper. 2015. No. 146. ST/ESA/2015/DWP/146.
Karnib A. Mapping the direct and indirect interlinkages across the sustainable development goals: A qualitative nexus approach // International Journal of Development and Sustainability. 2017. Vol. 6. No. 9. P. 1150-1158.
Oliveira A., Calili R., Almeida M.F., Sousa М. A Systemic and Contextual Framework to Define a Country's 2030 Agenda from a Foresight Perspective // Sustainability. 2019. No. 11. 6360. P. 1-28. DOI: 10.3390/su11226360
Nerini F.F., Tomei, J., To, L. S., Bisaga, I., Parikh, P., Black, M.Mulugetta, Y. Mapping synergies and trade-offs between energy and the Sustainable Development Goals // Nature Energy. 2017. No 3(1). P. 10-15. DOI: 10.1038/s41560-017-0036-5.
Weitz N., Carlsen H., Nilsson M., Skanberg K. Towards systemic and contextual priority setting for implementing the 2030 Agenda // Sustainability Science. 2018. No. 13(2). P. 1-29.
Bojtor, A., Czippan, K. The Synergies of the Sustainable Development Goals and the Good State and Governance Report in Hungary. 2019. URL: https://www.nispa.org/files/conferences/2019/e-procee-dings/system_files/papers/the-synergies-bojtor.pdf (дата обращения: 10.02.2024)
Mainali B., Luukanen J., Silveira S., Kaivo-Oja, J., Evaluating Synergies and Trade-Offs among Sustainable Development Goals (SDGs): Explorative Analyses of Development Paths in South Asia and Sub-Saharan Africa // Sustainability. 2018. Vol. 10. No 3. Р. 1-25.
Laumann F., Kugelgen J. von, Uehara T.H.K., Barahona M. Complex interlinkages, key objectives, and nexuses among the Sustainable Development Goals and climate change: a network analysis // Lancet Planet Health. 2022. Vol. 6 (5). P. e422-e430.
Cling J-P., Delecourt C. Interlinkages between the Sustainable Development Goals // World Development Perspectives. 2022. No. 25. P. 1-18.
Allen C., Metternicht G., Wiedmann T. National pathways to the Sustainable Development Goals (SDGs). A comparative review of scenario modelling tools // Environmental Science & Policy. 2016. Vol. 66. Р. 199-207.
Шаталов М.А. Исследование синергетических эффектов кластеризации в экономике регионов // Вестник Белгородского университета кооперации, экономики и права, 2017. № 6 (67). С. 119-129.
Побирченко В.В. Факторы устойчивого социально-экономического развития региона, синергия взаимодействия // Актуальные проблемы гуманитарных и естественных наук. 2017. № 4-3. С. 123-126.
Шевырев М.М. К методологии определения синергетического эффекта инновационных региональных кластеров // Экономика и управление, 2010. № 3 (53). С. 36-40.
Омаров Т. Д., Моргунова Н.В., Синявский Д.А. Подходы к оценке синергетического эффекта федеральных и региональных целевых программ (на примере Владимирской области) // Экономика и политика, 2013. № 6. С. 11-16.
Ярембаш А.И., Кохан Н.В. Эффект синергии в программах регионального социально-экономического развития // Механизмы управления экономическими, экологическими и социальными процессами в условиях инновационного развития: сб. матер. IV Межд. науч.-практич. конф.: в 2 ч. Алчевск: Донбасский государственный технический университет, 2018. С. 310-318
Паздникова Н.П. Моделирование регионального мониторинга государственных программ // Экономика и менеджмент систем управления. 2016. № 1-3(19). С. 337-342.
Warfield J.N. Developing Interconnection Matrices in Structural Modeling. IEEE Transcript on Systems, Men and Cybernetics. 1974. Vol. 4. No. 1. Pp. 81-87.
Shin N., Park S. Evidence-Based Resilience Management for Supply Chain Sustainability: An Interpretive Structural Modelling Approach // Sustainability. 2019. No. 11(2): 484. DOI: 10.3390/su11020484
Filho M.G., Monteiro L., de Oliveira Mota R., dos Santos Leite Gonella J., de Souza Campos L.M. The Relationship between Circular Economy, Industry 4.0 and Supply Chain Performance: A Combined ISM/Fuzzy MICMAC Approach. Sustainability. 2022.No.14. 2772. URL: https://doi.org/10.3390/su140527 (дата обращения: 12.03.2024)
Yin S., Wang Y. Establishment and Cluster Analysis of Performance Evaluation Index System for New Retail Enterprises Driven by Blockchain Technology // Journal of Service Science and Management. 2023. No. 16. Р. 535-566. DOI: 10.4236/jssm.2023.165029.
Chen J-K. Improved DEMATEL-ISM integration approach for complex systems // PLoS ONE. 2021. No. 16 (7): e0254694. URL: https://doi.org/10.1371/journal.pone.025469 (дата обращения: 12.03. 2024)
Mathiyazhagan K., Govindan K., NoorulHaq A., Geng Y. An ISM approach for the barrier analysis in implementing greensupply chain management // Journal of Cleaner Production. 2013. No. 47. P. 283-297.
Rezaeian A., Bagheri R. Modeling the Factors that Affect the Implementation of Knowledge Networks // Foresight and STI Governance. 2018. Vol. 12. No. 1. P. 56-67. DOI: 10.17323/2500-2597.2018.1.56.67
Ahmad N., Qahmash A. SmartISM: Implementation and Assessment of Interpretive Structural Modeling // Sustainability. 2021. No. 13. 8801. URL: https://doi.org/10.3390/su13168801(дата обращения: 12.03. 2024)
Luthra S., Kumar V., Kumar S., Haleem, A. Barriers to implement green supply chain management in automobile industry using interpretive structural modeling technique: An Indian perspective // Journal of Industrial Engineering and Management. 2011. No. 4(2). Р. 231-257. DOI: 10.3926/jiem.2011.v4n2.p231-257
Gabus A., Fontela E. World Problems, an Invitation to Further Thought within the Framework of DEMATEL. Battelle Geneva Res. Center, Geneva, Switz. 1972.
Hsieh Y-F., Lee Y-Ch., Lin Sh-B. Rebuilding DEMATEL threshold value: an example of a food and beverage information system // Springer Plus. 2016. No. 5:1385. DOI: 10.1186/s40064-016-3083-7
Shao J., Taisch M., Ortega-Mier M. A grey-DEcision-MAking Trial and Evaluation Laboratory (DEMATEL) analysis on the barriers between environmentally friendly products and consumers: practitioners' viewpoints on the European automobile industry // Journal of Cleaner Production. 2016. No. 112. P. 3185-3194.
Rajesh R., Ravi V. Modeling enablers of supply chain risk mitigation in electronic supply chains: A Grey-DEMATEL approach // Computers & Industrial Engineering. 2015. No. 87. P. 126-139.
Lenth R.V. Quick and Easy Analysis of Unreplicated Factorials // Technometrics. 1989. Vol. 31(4). P. 469-473. DOI: 10.1080/00401706.1989.10488595
Lohana Y.K. ISM and MICMAC Model for Construction Delay // Research Journal of Engineering and Technology. 2021. Vol. 8 (1). P. 1382-1391.

Еще

Статья научная