Структурный синтез двухподвижного пространственного 5R механизма и элементы следящего управления

Механизм Беннетта, впервые описанный английским математиком Беннеттом [1], является пространственным четырехзвенным (4R) механизмом с непараллельными и непересекающи-мися осями. В механизме противолежащие звенья попарно равны и отношение длин звеньев равно отношению синусов углов скрещивания соответственно.

Пространственный 4R механизм является одним из самых простых пространственных механизмов, преобразующий входное движение в одной плоскости в выходное движение другой плоскости, и служит “отправной точкой” для синтеза более сложных пространственных многозвенных механизмов с вращательными парами.

П. Г. Мудров в статье [2] описал способ получения пространственных механизмов с вращательными парами и с числом звеньев, больше четырех, используя способ объединения пространственных 4R механизмов. В частности, им были получены пятизвенный (5R) механизм, путем объединения двух пространственных 4R механизмов, и 11 видов шестизвенных механизмов. В статье [3-5] также описываются способы получения пространственных шарнирных механизмов, в частности, пространственного 5R механизма на базе двух одинаковых шарнирных четырехзвен-

ников. Все, полученные таким путем, механизмы имеют кривошипы (ведущее звено совершает полный оборот относительно неподвижного звена) и единичную подвижность ( W=1 ).

СПОСОБ ОБРАЗОВАНИЯ

ПРОСТРАНСТВЕННОГО 5R МЕХАНИЗМА

Наряду с этим, существует еще один способ получения пространственного 5R механизма. Возьмем за основу пространственный 4R механизм (рис. 1а). Не изменяя структурных параметров этого механизма, но освободив звено 4 и добавив одно дополнительное звено – стойку 5, можно получить двухподвижный 5R механизм (рис. 1б).

Для наглядности на рис. 2 представлены действующие модели пространственных 4R и 5R механизмов, изготовленных методов 3D печати.

Для нового 5R механизма степень подвижности по формуле Малышева-Сомова, равна:

W = 6 - ( n - 1) + 5 - p ₅ + 5 = 6 • (5 - 1) - 5 - 5 + 3 = 2 , (1)

где n – число звеньев, p5 – число кинематических пар пятого класса (вращательных пар), s –число согласованных размеров.

W = 2 показывает, что механизм двухподвижен и может иметь два ведущих звена (звено AB и звено AD ).Угол поворота γ между ведущим шатуном AB и ведомым кривошипом CD зависит от углов поворота ϕ ведущего кривошипа AB , λ ведущего шатуна AD , и вычисляется по одной из представленных формул (2) и (3):

cos w - cos X-K + sin w - sin X-K - (cos² Я - sin² X ) - K - K.

cos y =------------¹------------²-----5-----5----³——

- cos w • cos X■ K 5 + sin ф■ sin X■ K 6 + (cos X - sin X ) - K 7+ K 8

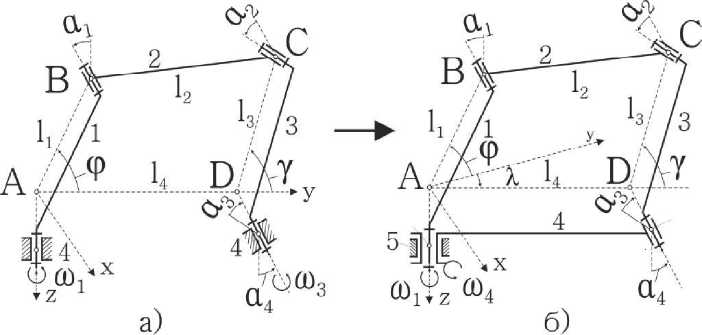
Рис. 1. Схема получения пространственного пятизвенного механизма с вращательными парами

Рис. 2. Экспериментальные модели пространственных а – 4R, б – 5R механизмов

(sin ф - cos X + sin X - cos ф ) - (1 2 - 1 2 )

- cos ф - cos X-K ₅ + sin ф - sin X-K ₆ + (cos ² Л - sin ² X ) - K 7 +K 8

,(3)

где K 1 = 1 ₂ ² - cos a 1 + 1 1² - cos a ₂ ,

K ₂ = 1 1² - cos a ₂ - 1 ₂ ² - cos a 1 ,

K 3 = 1 1 - 1 ₂ - cos a ₂ ,

K 4 = 1 1 - 1 ₂ - cos a 1 ,

K 5 = 1 1 - 1 2 - (cos a 1 + cos a ₂) ,

K ₆ = 1 1 - 1 2 - (cos a 1 - cos a ₂) ,

K 7 = 1 1² - cos a ₂ ,

K 8 = 1 ₂ ² - cos a 1 .

Дифференцируя выражение (3) по времени, получим угловую скорость рабочего звена относительно рабочего шатуна:

w ₂

A 1 + A 2

(-MK + MK+CM - MTlK T + KTcos / , (4)

где A = N 1 - (M 1 M 4 (K 5 + K₆) + (M , - M 4 ) .

. (K 7 (M 6 -M 5 )-K 8 )-M 1² K 6 -M ²4 K 5 ) ,

A 2 = N ₂ M 7 (M₂ + M 3 ) - M 2 N 3 - M 2 N 4 - M , M 3 N ₅,

^N 1 = ⁽¹2 - ^{12) - (} w i ⁺ w 4 ) ,

N 2 = 4 - (1 2 - 1 2 ) - W 4 - K 7 ,

N 3 = (1 2 - 1 2 ) - (W i - K 5 + W 4 - K ₆) ,

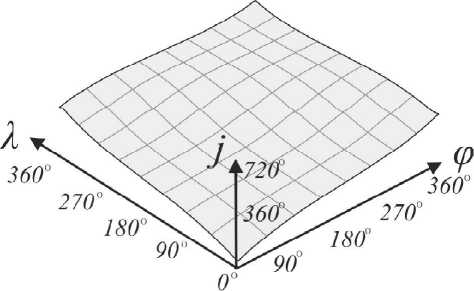
Рис. 3. График угла поворота ведомого кривошипа

N 4 = (1 2 - 1 2 ) - (W 4 - K 5 + W i - K б ) ,

N 4 = (1 2 - 1 2 ) - (W i + W 4 ) - ( K 5 + K б ) ,

M 1 = sin ф - sin X ,

M ₂ = sin ф - cos X ,

M 3 = cos ф - sin X,

M 4 = cos ф - cos X,

M ₅ = cos ² X ,

M ₆ = sin ² X,

M ₇ = sin X - cos X .

По результатам анализа уравнений (2) - (4) выявлено, что при равномерном вращении ведущего кривошипа ( w ₁=const) и ведущего шатуна ( w ₄=const) относительно неподвижной системы координат xyz , вращение ведомого кривошипа относительно ведущего шатуна является неравномерным и зависит от значений угловых параметров ϕ и λ . При вращении ведущего кривошипа и ведущего шатуна на один полный оборот относительно неподвижной системы координат xyz, ведомый кривошип может совершать несколько полных оборотов относительно ведущего шатуна. На рис. 3 представлен график вращения ведомого кривошипа для пространственного 5R механизма со структурными параметрами l₁ = 100, l₂ = 200, α₁= 30 ^o , α₂= 90 ^o при w ₁=const и w ₄=const .

КИНЕМАТИКА ХАРАКТЕРНЫХ ТОЧЕК

Для пространственного 4R механизма при неподвижном звене AD (рис. 1а) с заданными структурными параметрами l₁, l₂, б₁, б₂ движение характерной точки С звена CD описывается уравнением (5) и зависит только от угла поворота ф ведущего звена:

в пространстве и его угол поворота относительно ведущего шатуна (звено AD). Движение характерной точки С в данном случае описывается уравнением (6) и зависит от двух входных угловых параметров ф и X :

X C = -1 , - sin ф + 1 2 sin у- cos a , - cos ф-1 2 cos у- sin ф

C : Y = 1 , - cos ф + 1 2 sin у- cos a _l- sin ф + 1 2 cos у- cos ф (6)

Х_с = - 1 1 - sin ф + 1 2 sin у- cos a , - cos ф - 1 2 cos / - sin ф

Z_C = - 1 ₂ - sin у - sin a ,

Y _C = 1 1 - cos ф + 1 2 sin у- cos a , - sin ф + 1 2 cos у- cos ф (5)

ZC = -12 -sinу-sina sin ф - K где sin у =---------3—,

K 1 - cos ф - K₂

K, - cos ф - K cos у = —1---------2

K 1 - cos ф - K₂ ’

K , = 1 2 - cos a , + 1, • cos a ₂ ,

K ₂ = 1 1 - 1 ₂ - (cos a , + cos a ₂) ,

K 3 = 1 22 - 1 12 .Траекторией движения данной точки является окружность O с центром в точке D и радиусом l₁ . Регулируя угол скрещивания осей б₂ можно влиять на взаимное расположения оси Aa шарнира A и плоскости окружности О (рис. 4).

Изменяя значение входного параметра ф можно установить характерную точку С рабочего органа CD на любую точку окружности О . При этом для каждого значения входного параметра ф существует лишь одна точка на окружности О и наоборот.

Основным отличием нового 5R механизма является то, что он имеет два входным параметра: углы поворота ведущего кривошипа ф и ведущего шатуна X относительно неподвижной оси y базовой системы координат xyz (рис 1б). Управляя входными параметрами можно регулировать положение рабочего органа (звено CD)

где cosф• cos X K +sinф■ sinX-K -(cos2 X-sin2 X) - K - K cosy=-----------1------------2-----,-----,---3——

- cos ф - cos X - K 5 + sin ф - sin X - K _; + (cos X - sin X ) - K 7 + K 8 ’

(sin ф - cos X + sin X ■ cos ф ) - (1 2- 1?) sin у =--------------------------------т-2—---------

- cos ф - cos X■ K 5 + sin ф - sin X■ K 6 + (cos X - sin X ) - K 7 + K 8 ,

K 1 = 1 2 -cos a 1 + 1 2 -cos a ₂ ,

K 2 = 1 12 -cos a ₂ - 1 2 -cos a 1 ,

K 3 = 1 1 - 1 2 - cos a ₂ ,

K ₄ = 1 1 - 1 2 - cos a , ,

K ₅ = 1 i - 1 2 - (cos a , + cos a ₂) ,

K ₆ = 1 1 - 1 2 - (cos a , - cos a ₂) ,

K 7 = 1 12 - cos a ₂ ,

K 8 = 1 2 - cos a , .

В результате анализа уравнения (6) установлено, что траекторией точки С является поверхность вращения, образованная вращением окружности О радиуса l₁ вокруг прямой Aa , являющейся осью шарнира А (рис. 5а). Расстояние от центра окружности О до прямой Aa равно l₂ . В частном случае, когда один из структурных параметров угол a₂ = 90 o , то образующая окружность О и ось вращения Аа лежат в одной плоскости. В результате образуется поверхность вращения – тор (рис 5б).

Изменяя скорость вращения ведущих звеньев AB и AD относительно неподвижной системы координат xyz , можно влиять на траекторию движения характерной точки С. В табл. 1 представлены с разных ракурсов несколько вариантов траекторий движения в зависимости от скорос-

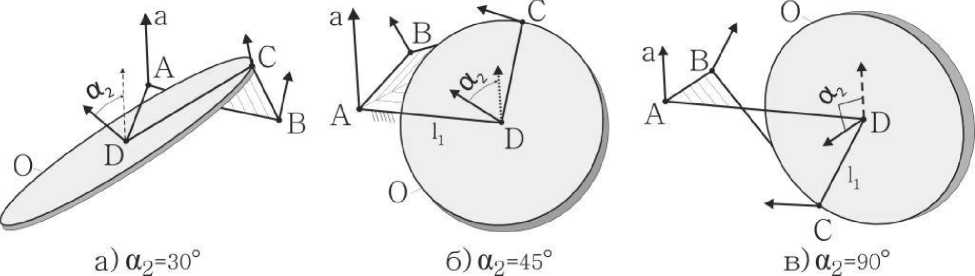
Рис. 4. Взаимное расположение траектории характерной точки С с осью шарнира A

Рис. 5. Траектории движения характерной точки С для 5R механизма

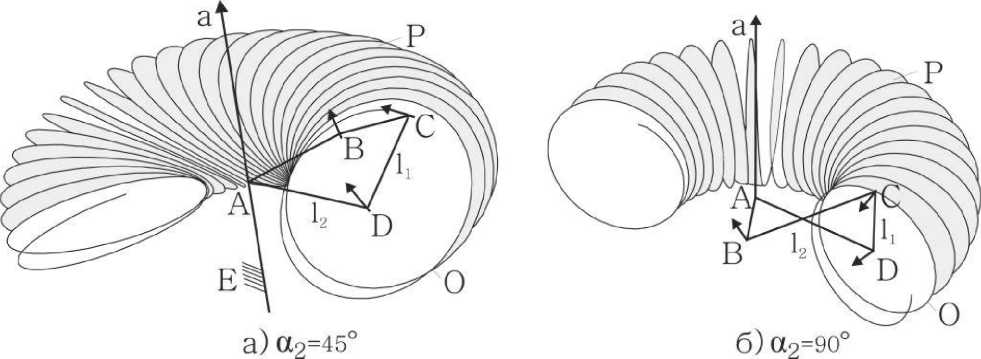
Таблица 1. Траектория движения характерной точки С

№	Скорость вращения (рад/сек)	Результат. Траектория движения	№	Скорость вращения (рад/сек)	Результат. Траектория движения
1	W 1 = 0.2 W 2 = 0.1	f	4	W 1 = 2 W 2 =2.1	Vx/б    Ay
2	W 1 = 0.3 W 2 = 0.6		5	W 1 = 2.0 W 2 =2.3
3	W 1 = 0.2 W 2 =0.3	Ap V............ '^JlV	6	W 1 = 2.3 W 2 =1.3

тей вращения ведущих звеньев пространственного 5R механизма со структурными параметрами l₁ = 100, l₂ = 200, α₁= 30 ^o , α₂= 90 ^o . Все представленные траектории движения лежат на одной и той же поверхности вращения P.

В работе [6] автор решает обратную задачу для плоского пятизвенного двухподвижного механизма с вращательными парами. Он определяет угловые координаты входных звеньев, обеспечивающих попадание характерной точки двухподвижного манипулятора в точку с заданными координатами x и y. Для решения обратной задачи в нашем случае используем метод, который можно охарактеризовать как “следящее управле- ние”. Воспользуемся программным комплексом 3D моделирования и проектирования SolidWorks и спроектируем пространственный 5R механизм ABCDF и на продолжении оси шарнира С закрепим сферу S с центром в точке O [7-9]. Отдельно установим и закрепим неподвижную систему координат xyz таким образом, чтобы начало системы совпало с центром шарнира А, ось z совпала с осью Аа шарнира А, ось y лежала на плоскости, образованная двумя линиями кратчайших расстояний ведущих звеньев AB и AD, а ось x направим таким образом, чтобы в результате получилась правая прямоугольная система координат xyz (рис. 6).

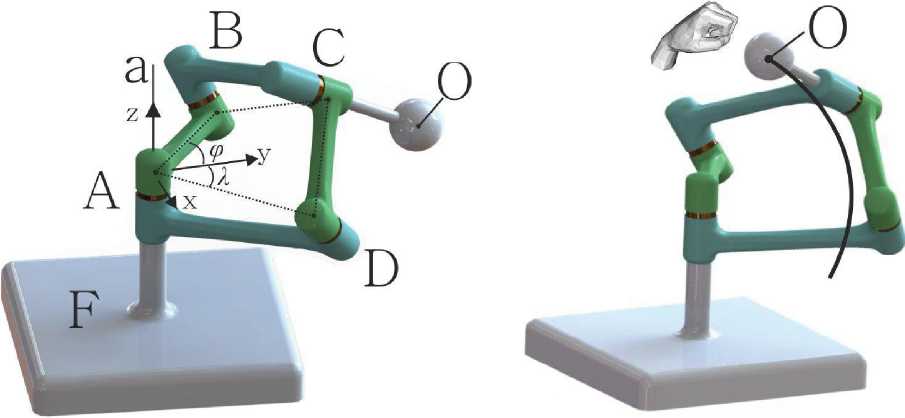
Рис. 7. Управление 5R механизмом при помощи инструмента “рука”

Рис. 6. Компьютерная модель 5R механизма

На звено AB установим датчик угла поворота D₁ (на рисунке не указан), который будет измерять значение угла поворота ϕ звена AB относительно оси y неподвижной системы координат xyz . Аналогично, на звено AD установим датчик угла поворота D₂ (на рисунке не указан), который будет измерять значение угла поворота λ звена AD относительно оси y неподвижной системы координат xyz .

Метод “следящее управление” состоит из двух этапов. На первом этапе перейдем в режим “анализ движения” и, используя инструмент “рука”, начнем перемещать сферу S в пространстве (рис. 7). При этом центр данной сферы точка O будет описывать траекторию, которая лежит на поверхности вращения, образованная вращением окружности с центром в точке C и радиусом l₁ вокруг оси Aa шарнира A . Датчики угла поворота D₁ и D₂ будут замерять значения углов ϕ и λ , на которые повернулись ведущие звенья AB и AD относительно оси y неподвижной системы координат xyz соответственно.

На втором этапе использования метода на звенья AB и AD вместо датчиков угла поворота необходимо установить сервоприводы и подавать на них управляющие воздействия, снятые с датчиков D1 и D2. При этом точка O сферы S будет перемещаться по вычисленной траектории движения. В табл. 2 представлены результаты работы данного метода.

Практическое использование пространственного двухподвижного 5R механизма

Одним из направлений применения пространственных механизмов с вращательными парами являются использование их как базовых механизмов активаторов различных технологи- ческих процессов [10-12]. В результате анализа кинематики пространственного двухподвижного 5R механизма установлено, что характерные точки механизма движутся по сложной траектории вращения с переменными скоростями и ускорениями. Анализ работы компьютерных моделей механизма показывает, что такая кинематика рабочего звена и характерных точек емкости смесителя способствует качественному перемешиванию компонентов. На базе пространственного 5R механизма изготовлена лабораторно-экспериментальная установка управляемого многорежимного 3D миксера.

Ведущие звенья 1 и 2 пространственного 5R механизма приводятся в движение с помощью двух мотор-редукторов, скрытых в корпусе 5. На рабочее звено 3 закрепляется съемный барабан 4, в котором находятся перемешиваемые компоненты. Частотные преобразователи 6 и 7 позволяют регулировать скорость вращения ведущих звеньев базового механизма. В случае необходимости барабан 4 может быть заменен на другой барабан другого объема и формы, может быть использован для перемешивания как жидких, так и сыпучих веществ.

ЗАКЛЮЧЕНИЕ

В работе представлен способ образования пространственного двухподвижного 5R механизма на базе пространственного одноподвижного 4R механизма. Проведен анализ кинематики характерной точки рабочего звена и определены её траектории движения. Решена обратная задача для пространственного 5R механизма методом “следящего управления” и предложен один из вариантов при-

Таблица 2. Расчет значений входных параметров по заданной траектории движения

№

Заданная траектория

Результат вычислений

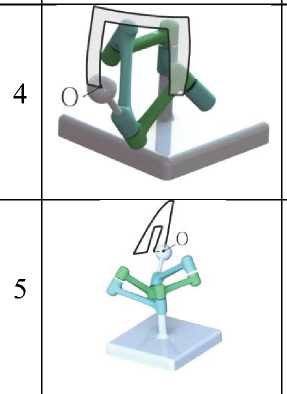
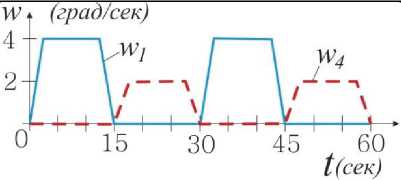
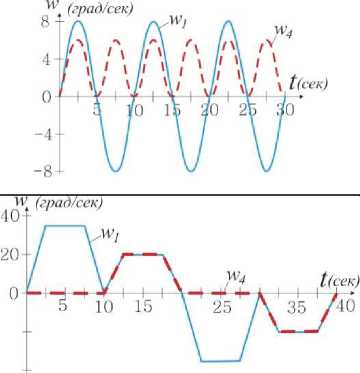
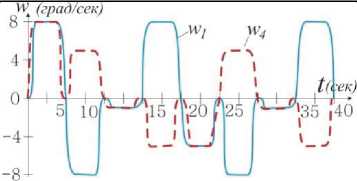
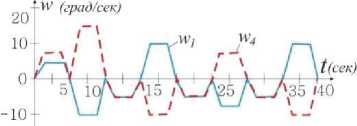
Рис. 8. Лабораторно-экспериментальная установка 3D ЛЭМ: а – без барабана, б – с барабаном для перемешиваемых компонентов

менения механизма в качестве управляемого многорежимного 3D миксера, позволяющего высококачественно перемешивать компоненты, резко отличающихся в долевом соотношении.