Stuckelberg particle in external magnetic field. Nonrelativistic approximation. Exact solutions

In previous paper [1], we studied the relativistic Stuck-elberg tensor system (see the references in [1]) of11 equations in presence of the external uniform magnetic field. The relativistic particle is described by 11-component wave function, consisted of scalar, vector, and antisymmetric tensor. On so- lutions there are diagonalized operators of energy, the third projection of the total angular momentum, and the third projection of the linear momentum along the magnetic field direction. After separating the variables, the system of 11 radial functions was derived, and it was solved in the terms of con- fluent hypergeometric functions. Three series of the energy levels are found.

In the present paper we study the non-relativistic approximation for this problem. We apply the well-known method (see [2–4]) from the general theory of relativistic wave equations, based on the minimal equation for the matrix Г _о (in the model under consideration, it is an 11 x 11-matrix). This minimal equation allows us to introduce three projective operators P + , P _- , P 0 and then expand the wave function into three components: Ф = Ф + + Ф _ + Ф _о . From the general theory it is known that when obtaining the nonrelativistic approximation the components Ф _ and Ф _о should be considered as small, and Ф + — as large ones. Only the component Ф + enters the nonrelativistic equation. The nonrelativistic wave function turns out to be 4-dimensional. We derive the radial system for 4 functions. It is solved in terms of confluent hypergeometric functions. There arise three series of energy levels with corresponding solutions. This result agrees with that obtained for relativistic Stuckelberg equation.

1.    Nonrelativistic approximation and projective operators

We start with the matrix Г _о of the basic Stuckelberg equa-

tion (see [1]) 0 -1 0 0 0   0    0    0   0 0 0 1 0 000 0  0  0 000 0   0   0 0 0 -1   0    0   0 0 0 0   0   0 0 0   0   -1   0   0 0 0 0   0   0 0 0   0    0   -1 0 0 0 Го = 0 0 100 0  0  0 000 . 0 0 010 0  0  0 000 0 0 001 0  0  0 000 0 0 000 0  0  0 000 0 0 000 0  0  0 000 0 0 000 0  0  0 000 (1) It obeys the minimal equation Г(Г2 + 1) = 0, which permits us to define three projective operators

P о = 1+r 0 ,  P i = P + =2 i Г( i Г + 1) ,

P 2 = P _ = 2 i Г( i Г - 1)            (2)

with the properties

P = P о ,  P + = P + ,  P _ = P _ ,

P о + P + + P _ = I.

In accordance with this, the complete wave function may be decomposed into the sum of three parts

Ф = Ф + + Ф _ + Ф о ,

Ф + = P + Ф , Ф _ = P _ Ф ,  Ф о = P о Ф .   (3)

It is known from the general theory that in nonrelativistic approximation the component Ф + should be considered asa big one, whereas the components Ф - , Ф о — as small ones. We readily find their explicit structure:

Ф + = 2 ( h - i Ф о ,i ( H - i Ф о ) , Ф 1 - iE 1 , Ф ₂ - iE 2 ,

Ф з -iE з ,i (Ф 1 -iE i ) ,i (Ф 2 -iE 2 ) ,i (Ф 3 -iE 3 ) , 0 , 0 , 0) t =

= ( L о , iL о , L 1 , L 2 , L 3 , iL 1 ,iL 2 ,iL 3 , 0 , 0 , 0) t ,

Ф _ = 2 ( h + i Ф о , -i ( H + i Ф о ) , Ф 1 + iE 1 , Ф 2 + iE 2 ,

Ф 3 + iE 3 , -i (Ф 1 + iE 1 ) , -i (Ф 2 + iE 2 ) ,

• -i (Ф 3 + iE 3 ) , 0 , 0 , 0) t =

= ( S о , -iS о , S 1 , S 2 , S 3 , -iS 1 , -iS 2 , -iS 3 , 0 , 0 , 0) t , Ф о = (0 , 0 , 0 , 0 , 0 , 0 , 0 , 0 , B 1 , B 2 , B 3 ) t ,       (4)

where t stands for transpose. We have introduced special notations for big and small functions.

Because when solving the relativistic problem [1], we used the cyclic basis, now we also should transform big and small component to this basis. Because all blocks of the matrix Г ^о preserve their form in cyclic basis,

Д ^о = (1 , 0 , 0 , 0) t ,   -G ^о = ( - 1 , 0 , 0 , 0) ,

/ 0    0    0   0  00

к о - | -1   0    0   0  00

K  = I  0   -1   0   0  00

\ 0    0   -1  0  00/

0 0 1 0 0 1 0 0 Lо = 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 we conclude the rule for obtaining big and small components remains the same in this known basis:

p 3 = 1 + г о ,

_____                                 I          _____ _____ _____ I          _____ _____

P + = ₂ i Г( i Г + 1) ,  P _ = ₂ i Г( i Г - 1) .

The formulas (4) may be written in more convenient variables as follows:

Ф + — 2 ( h - ih о , i ( h - ih о ) , h 1 - iE 1 , h 2 - iE 2 , h 3 -iE 3 , i ( h 1 -iE 1 ) , i ( h 2 -iE 2 ) , i ( h 3 -iE 3 ) , 0 , 0 , 0) t = = ( L о , iL о , L 1 , L 2 , L 3 , iL 1 , iL 2 , iL 3 , 0 , 0 , 0) t , Ф _ = 2 hh + ih о , -i ( h + ih о ) ,h 1 + iE 1 ,h 2 + iE 2 , h 3 + iE 3 , -i ( h 1 + iE 1 ) , -i ( h 2 + iE 2 ) ,

• -i ( h 3 + iE 3 ) , 0 , 0 , 0) t = = ( S о , -iS о , S 1 , S 2 , S 3 , -iS 1 , -iS 2 , -iS 3 , 0 , 0 , 0) t ,

Ф о = (0 , 0 , 0 , 0 , 0 , 0 , 0 , 0 , B 1 , B 2 , B 3 ) t .       (5)

Hence we can derive inverse expressions for initial variables through big and small components:

h = 2(L0 + S0),  h0 = i2(L0 - S0), hi = 2(Li + Si),   Ei = i2(Li - Si),      (6)

i = 1 , 2 , 3 .

Now we turn to relativistic system of equations (see in [1]), collecting them in 4 pairs and one triple:

— ieh 0 — ikh 2 +-- h’h-— —

( Br ² + 2 m — 2) h

2_X 2 r

-

Eliminating the small components B 1 , B 2 , B 3 with the help of three last equations we get

-iϵh 0	Br 2 + 2 m - 2 7 2 r	2- h 1	Br 2 + 2 m + 2 ikh2              h g + 272 r
	+	1	dh 1     1 dh 3
		72	dr   72 dr     ц,
- iϵh	- ikE 2 + 72	dE 1 dr	Br 2 + 2 m - 2 -          E 1 - 272 r
	1 dE 3	Br 2 + 2 m + 2
	7 2 dr		272 r         °'"”

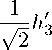
( Br ² + 2 m + 2) 2 72 r

^h 3 = ^—^h,

( Br ² + 2 m ) ц i.pE — ⁽ ’— h + 272 r

-

ieh — ikEo + ^E ‘

72 ¹

( Br ² + 2 m — 2)

-E 2_X 2 r

+

—B ² r ⁴ + ( — 8 k ² — 4 Bm ) r ² — 4( m — 1) ² 8 r ²

h 1 +

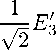
( Br ² + 2 m + 2) 2 7 2 r

E 3 = цh 0 ;

( Br ² + 2 m ) ik h

2 7 2 r     ²

1 , m + Br ² / 2     1 ,

--h^-- r- h + -Bl +

72      72 r      72 ²

( Br ² + 2 m )

+ -------- -B 2 — ikB 3 + ieE 1 = цh 1 ,

2 2 r

+ 1   + ⁽ Br ² + ² m )  — ie = ^e ;

72 ⁰      272 r

+

B ² r ⁴ + 4 B ( m + 1) r ² + 4 m¹²

8 r ²

— 4

h 3 ^-

ikh + ieE 2

-

7 B ‘

72 ¹

-

( Br ² + 2 m + 2)

4= h ‘

-

—   B ‘ +

72 3

272 r

( Br ² +2 m — 2) 2 7 2 r

—ikh 0 — ieh 2 = цE 2 ;

m + Br ²

7 2 r

/ 2

h + ' B ‘ 72 ²

-

B 1

-

B 3 = ^h 2 ,

ц dh 1 dh 1 ik dh 2 72 dr 2 r dr 72 dr

+ Br ² + 2 m + 1 dh 3 + 1 d ² h 1 + 1 d ² h 3    2 h

2 r dr 2 dr ²     2 dr ^{2     Ц 1}

⁽ Br ^{2 + 2 m} ) Ц     .        Ц ^dh 0    2

--—=---h 0 ^— i^h 1 ⁺ — — = Ц E 1 ;

2 2 r                   2 dr

(Br2 + 2m — 2)ik ieuE 2 + ikuh--—h

272 r

( Br ² + 2 m ) ²      ( Br ² +2 m + 2) ik

4r2     2        272r ik dh 1 + 1 dh2    ik dh3 + d2 h22

72 dr   r dr   72 dr dr ² Ц ²

—ikцh 0 — ieцh 2 = ц ² E 2 ;

-

( Br ² + 2 m )

B 2 + ikB 1 + ieE 3 = ^h 3 ,

272 r

-

-

-

+

7 12 h	‘ Br 2 + 2 m 0 +   2 7 2 r h 0 ieh 3 =	: цЕ 3 ;
7 12 h	Br 2 + 2 m 2 +      r-   hs + ikha = 2      272 r	µB 1 ,
ikh 1	_ 1 h — Br 2 + 2 m h = 72 2     272 r	µB 3 ,
h ′ 1 -	Br 2 + 2 m - 2 h 1 + 272 r 1 h Br 2 + 2 m + 2 7 2 3       2 7 2 r	h 3 = цB 2

.

■        (Br2 + 2m)Ц K , ieцEз------h+

272 r

B ² r ⁴ + 4 B ( m — 1) r ² + 4 m ²

⁺             8 r 2

( Br ² + 2 m ) ik h

2 7 2 r     ²

⁴ h 1 +

-B ² r ⁴ + ( - 8 k ² - 4 Bm ) r ² - 4( m + 1) ²

+-------!sr^5h 3+ ц dh Br2 + 2m — 1 dh 1

72 dr        2 r      dr

ik dh ₂

7 2 dr

! 1 dh 3 ! 1 d ² h 1 ⁺ 2 r 17 ⁺ 2 " dr ²"

1 d ² h 3

⁺ 2 dr^{1 2}

= ц ² h 3 ,

( Br ² + 2 m ) 1     .        1 dh 0    2

—=    h 0 — ie^h 3   7=    — ¹ E 3 .

2 2 r                   2 dr

Let us take into account the formulas (2), this results in pair I

Br ² + 2 m — 2

^{e (} L 0 ^— S 0 )2 ^— 2 _r ----⁽ L 1 ⁺ S i ) ^—

Br ² + 2 m + 2

^—ik ^{( L} 2 ⁺ S 2⁾------- ^{( L} 3 ^{+ S} 3 ^{) +}

2 2 r

+ ik d ( L 1 + S 1 ) + 1 d ( L 2 + S 2 )

22    dr r dr

ik d ( L 3 + S 3 )

—2   dr

+ ^{d 2 ( L}dr + ^{S 2 )} — 1 ² ( L 2 + S 2 ) ■

—ik1 ( L 0 — S 0 ) — e1 ( L 2 + S 2 ) — 1 ² ( L 2 — S 2 );

+

pair IV

—ец ( L 3 — S 3 ) — ⁽ Br 2 - J m ^{) 1} ( L 0 + S 0 ) +

B ² r ⁴ + 4 B ( m — 1) r ² + 4 m ² — 4

⁺------- ^r^--------- ^{( L} 1 ^{+ S} 1 ^{) +}

( Br ² + 2 m ) ik

⁺     2 7 2 r    ⁽L 2 ⁺ S ^{2 )+}

—B ² r ⁴ + ( — 8 k ² — 4 Bm ) r ² — 4( m + 1) ²

⁺-------'------8 r^   ( ^L 3 + ^S 3 )⁺

1 d ( L 0 + S 0 ) Br ² + 2 m — 1 d ( L 1 + S 1 )

22    dr            2 r         dr

-

1 d ⁽ L 1 + S 1 )    1 d ⁽ L 3 + S 3 )

2 dr

2 dr

^{1 (} L ^{( L} 0 ^{+ S} 0 ) ,

—e ( L 0 + S , ) — ik ( L 2 — S 2 ) + — d ⁽ L ¹    S ^{1 )}

2 2     dr

-

Br ² + 2 m — 2

2 V2 r    ⁽L ^{1 —} S 1 )

-

-

-

^{1 d ( L} 3 ^— S 3 ⁾

/2     dr

-

^{Br 2 + 2} m ^{+ 2}

—2 ^ 2 r —^{( L} 3 ^— S 3 )^— 1 ^{( L} 0 ^— S 0 );

pair II

—e^ ( L 1 — S 1 ) — (-B—m¹ ( L 0 + S 0 )+

—B ² r ⁴ + ( — 8 k ² — 4 Bm ) r ² — 4( m — 1) ²

⁺----------'--------₈-------'------- ( ^L 1 + ^S 1 ) ⁺

( Br ² + 2 m ) ik

⁺     2 ^— 2 r    ⁽ L 2 ⁺ S 2 ⁾⁺

B ² r ⁴ + 4 B ( m + 1) r ² + 4 m ² — 4

⁺              8 r 2               ^{( L 3 +} S ^{3 ) —}

_ 1 d ( L 0 + S 0 ) ₊ I d ( L 1 + S 1 ) ₊

22    dr 2 r dr

+ ik d ( L 2 + S 2 ) + Br ² + 2 m + 1 d ( L 3 + S 3 ) +

22    dr            2 r         dr

ik ^{d ( L} 2 ^{+ S} 2 ⁾ + ^{1 d ( L} 3 ^{+ S} 3 ⁾ +

22    dr      2 r    dr

+1 d ² ( L_x + S 1 ) + 1 d ² ( L₃ + S 3 )

^— 1 ^{2 ( L} 3 ^{+ S} 3 ⁾ ,

( Br ² + 2 m ) 1 2 -2 r

( L 0 — S 0 )

^{— e}1 ^{( L} 3 ^{+ S} 3 ^{) —}

1 ^{d ( L} 0 ^{— S} 0 ⁾

—2   dr

^— 1 ^{2 ( L} 3 ^{— S} 3 ⁾ •

1 d ² ( L 1 + S 1 )1 d ² ( L 3 + S 3 )     2_(T _

⁺ 2---- dr 2----+ 2---- dr 2---- = ^{1 (} L ^{1 + S 1 )} ’

^{( Br 2 + 2 m )} 1        _A

2 ^— 2 r    ^{( L} 0 ^{— S} 0 ^{) — e1 ( L} 1 ^{+ S} 1 ⁾⁺

1 d ( L 0 — S , )

^{+ —}---dr— ^{— 1 ( L 1 —} S ^{1 )1}

Within each pair, let us sum and subtract equations, this results in:

pair I

Br ² + 2 m — 2            Br ² + 2 m + 2

7=       L ₃ + 2 ikL 2 +--7=       L 3 —

V2 r                   2r r

— — dL ¹ + —2 dL ³ +2 eS 0 — 2 1S 0 , dr dr

pair III

— e1 ( L 2 — S 2 ) + ik1 ( L 0 + S 0 ) —

-

( Br ² + 2 m — 2) ik 2 — 2 r

( L 1 + S 1 ) —

-Br ² - 2 m + 2

2 eL 0 +------------- S 1 —

2 r

-

⁽ Br ^{2 + 2} m ^{) 2}

4 _r 2      ^{( L 2 +} S ^{2 )}

- 2 ikS 2 -

Br ² + 2 m + 2

— 2 r

S 3 +

^{( Br 2 + 2 m + 2) ik}

------ -2 ------ ^(L 3 ^{+ S} 3 ^{) +}

+ — 2 dS ! ^—2-2 dS 3 — — 2 1L 0 ; dr dr

( Br ² + 2 m ) ц

2_X 2 r

⁽ L о — S o ) — e^ ⁽ L 1 + S 1 )+

+    (LT¹ — dS ⁰) — ец ( L 1 — S 1 ) —

2 dr dr

-

( Br ² + 2 m ) ц

2X2 r

⁽ L 0 + S 0 ^{) +}

^—ец ^{( L} 2 ^{— S} 2 ) ^{+ ik}Ц ^{( L} 0 ^{— S} 0 )

-

-

-

⁽ Br ^{2 + 2} m ^{— 2)} ik

-----2 V 2 r-----⁽L ^{1 +} S 1 ) ^—

-

( Br ² + 2 m )

4 r 2

( L ₂ + S ₂ ) —

( Br ² + 2 m + 2) ik

-

+

8 r¹²

'^{2 — 4(} m - ^{1) 2} ( L 1 + S 1 )+

+

( Br ² + 2 m ) ik

2V2 r

⁽ L 2 + S 2 ^{) +}

⁽ L 3 + S 3 ) +

2X2 r

+ 7 dLL, + dS ,^ + 2 dr    dr	1 r	( dL 2 + dS 2 dr    dr
ik dL 3 dS 3 — 7 2 ( "A + "A)	+	d 2 L 2 + dS

-

-

—ikц ( L 0 — S 0 ) — ец ( L 2 + S 2) — 2 ц ² L 2 ;

B ² r ⁴ + 4 B ( m + 1) r ² + 4 m ² — 4

⁺--------------8 r 2-------------- ^{( L 3 +} S ^{3 ) —}

^—ец ⁽ L 2 ^— S 2 ) ^{+ ik}ц ⁽ L 0 ⁺ S 0 ) ^—

-

dL 0 + dS 0 A + £ (LU + dS 1 A + dr dr /    2 r \ dr dr /

-

( Br ² + 2 m — 2) ik

2X2 r

( L 1 + S 1 ) —

+ 7 dS + S )+

Br ² + 2 m + 1 ( dL 3    dS 3

dr dr

2 r

)

+

-

-

( Br ² + 2 m )

4 r ²

( L ₂ + S ₂ ) —

( Br ² + 2 m + 2) ik

-к

d ² L 1 dr ²

d ² S 1      1

⁺ "dA ) ⁺ 2 (

d ² L 3 dr ²

⁺ d S)^—2 ц ^{2 L} 1 ■

2X2 r

⁽ L 3 ⁺ S 3 ^{) +}

-

+

^—ец ^{( L} 1 ^— S 1 )

-

( Br ² + 2 m ) ц

2V2 r

⁽ L 0 ⁺ S o ⁾⁺

B ² r ⁴ + ( — 8 k ² — 4 Bm ) r ² — 4( m — 1) ²

8 r 2                   ^{( L} 1 ⁺ S 1 ⁾⁺

( Br ² + 2 m ) ik

⁺     2 7 2 r    ⁽L ^{2 +} S ^{2 ) +}

+

B ² r ⁴ + 4 B ( m + 1) r ² + 4 m ² —

8 r ²

( L 3 + S 3 ) —

-

dL 0 + dS 0 A + £ (LU + dS 1 A + dr dr у   2 r \ dr dr /

+. ' L +t)+

Br ² + 2 m + 1 ( dL 3    dS 3

dr dr

2 r

)

ik (d L 1 dS A    1 (d L 2 dS 2A

^{+ 7} A^{+   +} Ad^ ⁺

pair IV

-

-

dL 3 + dS 3 A + d ² L 2 + d ² S 2 + dr dr dr ²     dr ²

+ ikц ( L 0 — S 0 ) + ец ( L 2 + S 2) — 2 ц ² S 2 ;

^—ец ^{( L} 3 ^{— S} 3 )

-

( Br ² + 2 m ) ц

2X2 r

⁽ L 0 ⁺ S 0 ^{) +}

+ B ² r ⁴ + 4 B ( m

-

1) r ² + 4 m ² —

8 r ²

— ( L 1 ⁺ S 1 ^{) +}

-

++

+

( Br ² + 2 m ) ik

2^2 r

⁽ L 2 ⁺ S 2 ^{) +}

B ² r ⁴ + ( — 8 k ² — 4 Bm ) r ² — 4( m + 1) ² 8 r 2                   ^{( L} 3 ⁺ S 3 ^{) +}

d ² L 1 dr ²

d ² S 1      1

⁺ "dU )⁺2(

d ² L 3 dr ²

d ² S 3

⁺ dr ² у

-

+ £ (dL ? + S

-

Br ² + 2 m — 2 r

1 (d L 1 dS A dr dr

-

-

( Br ² + 2 m ) ц

-

2X2 r

⁽ L 0 ^— S 0 ) ^{+ е}ц ⁽ L 1 ⁺ S 1 )

dL 2 + dS 2 A + £ (LU + dS 3 A + dr dr у   2 r \ dr dr /

-

-

µ dL 0 dS 0       2

7 5 L ^— 77j ^{— 2 ц S 1;}

■:(

d ² L 1 dr ²

d ² S 1      1

⁺ "dA ) ⁺ 2 \

d ² L 3 dr ²

d ² S 3

⁺ dr ² y ⁺

+

( Br ² + 2 m ) ц

2V2 r

^{( L} 0 ^{— S} 0 ) ^{— е}ц ^{( L} 3 ^{+ S} 3 ) ^—

Известия Коми научного центра УрО РАН, серия «Физико-математические науки» № 5 (57), 2022

-

µ dL 0 _- dS 0

V2 d dr dr у

= 2 ц ² L з ,

+

( Br ² + 2 m ) ik

2 _x 2 r

⁽ L 2 + S 2 ^{) +}

^—еЦ ^{( L} 3 ^{— S} 3 )

-

( Br ² + 2 m ) ц

2^2 r

⁽ L о + S o ⁾⁺

+

B ² r ⁴ + 4 B ( m + 1) r ² + 4 m ² —

8 r r ²

( L 3 + S 3 )+

+

B ² r ⁴ + 4 B ( m — 1) r ² + 4 m¹²

-

-

+

+

8 r ²

4,

-( L 1 + S 1 )+

+ M ddLo + dS 0 A + £ (dU + dS 1 A + ^ 2 \ dr dr у 2 r \ dr dr у

( Br ² + 2 m ) ik

2л/2 r

⁽ L 2 ⁺ S 2 ^{) +}

B ² r ⁴ + ( — 8 k ² — 4 Bm ) r ² — 4( m + 1) ²

8 r 2                  ^{( L 3 +} S ^{3 )+}

+

Br ² + 2 m + 1

2 r

/ dL 3 + dS 3 A + dr dr

+ ^ d^ + dS ⁰)

-

Br ² + 2 m — 2 r

1 (dL1  dSЛ dr dr

-

+ 2

( dL + dr ²

d ² S 1 dr ²

)+2 ( ddL 3 +

d ² S 3 dr ²

) = 2 M ² L 1 ,

-

dL 2 + dS 2 A + £ dLU + dS 3 A + dr dr у 2 r \ dr dr у

( M + E ) M ( L 1 —

S 1 ) +

( Br ² + 2 m ) M

2^2 r

⁽ L 0 ⁺ S o ⁾⁺

-

⁺2 drr ⁺

d ² S 1 dr ²

A + 1 d d L La + d ² S 3 A

У 2 \ dr ² dr ² J

-

-

( Br ² + 2 m ) ц

2^2 r

⁽ L 0 - S 0 ) ⁺ ец ( L 3 ⁺ S 3 ⁾⁺

+;A ( di? — dS O =2 ц ² L 3 •

The parameter µ relates to physical (positive) mass by the formula

ц = — M.

Let us separate the rest energy M by formal change е = M + E , where E is nonrelativisticenergy of the particle. The above equations become simpler:

pair I

Br ² + 2 m — 2

----------L 1 + 2 ikL 2 + 2 r

Br ² + 2 m + 2

V2r r

L 3 ^-

+

B ² r ⁴ + ( — 8 k¹²

— 4 Bm ) r ² — 4( m —

+

8 r ²

( Br ² + 2 m ) ik

¹⁾ ( L 1 + S 1 )+

+

2X2 r

⁽ L 2 ⁺ S 2 ^{) +}

B ² r ⁴ + 4 B ( m + 1) r ² + 4 m ² —

8 r ²

( L ₃ + S ₃ )+

-

2 dL ¹ + V 2 dL ³ + 2( M + E ) S 0 = dr dr

— 2 MS 0 ,

-Br ²

2( M + E ) L 0 +--

— 2 m + 2

2 r

S 1

-

2 ikS 2 —

Br ² + 2 m + 2

-

V2r r

√ dS 1

S 3 ^{+ 2} 2—— dr

-

2 dl r = 2 ML 0 ;

pair II

-

( Br ² + 2 m ) M

2V2 r

( L 0 — S 0 ) + ( M + E ) M ( L 1 + S 1 ) —

+ M 2 dLLo + dS₀

1 dL 1    dS 1

) ⁺ 2 r V"dr" ⁺ dr? ) ⁺

ik

+—7=

\2

+

/ dL 2 + dS 2 A + dr dr

Br ² + 2 m + 1

2 r

/ dL 3 + dS 3 A + dr dr

+ 2

( dL + dr ²

d ² S 1 dr ²

)+2 ( ddL 3 +

d ² S 3 dr ²

+

( Br ² + 2 m ) M

2^2 r

( L 0 — S 0 ) — ( M + E ) M ( L 1 + S 1 )+

⁺ M2 d^ — S) =² M ² S 1

pair III

( M + E ) M ( L 2 — S 2 ) — ikM ( L 0 + S 0 )

-

-

-

( Br ² + 2 m — 2) ik

2^2 r

( Br ² + 2 m + 2) ik

( L 1 + S 1 ) —

( Br ² + 2 m )

4 r ²

( L 2 + S 2 ) —

2V2 r

( L 3 + S 3 )+ d + dS i) + 2 dr dr

-

M2 (dL^{2 —} d r) ^{+( M +} E ’ ^{M ( L} 1

— S ₁ )+

+

( Br ² + 2 m ) M

2_X 2 r

( L ₀ + S ₀ )+

,1 / dL 2 ₊ dS 2 A _— ik (Lu ₊ dS 3 A ₊ r \ dr dr у    ^ 2 \ dr dr )

d ² L 2    d ² S 2

+ , 2 + Я 2 + ikM(L0 — S0) + dr2     dr2

+( M + E ) M ( L 2 + S 2 ) = 2 M ² L 2 ,

( M + E ) M ( L 2 — S 2 ) — ikM ( L 0 + S 0 ) —

-

+

B ² r ⁴ + ( — 8 k ² — 4 Bm ) r ² — 4( m — 1) ²

8 r 2                   ^{( L 1 +} S ^{1 ) +}

-

( Br ² +2 m — 2) ik

2X2 r

⁽ L 1 + S 1 ) ^—

( Br ² + 2 m )

4 r ²

( L 2 + S 2 ) —

-

( Br ² + 2 m + 2) ik

2\ 2 r

( L 3 + ? 3 ) + J dL + d? ¹) + 2 dr dr

^— M dL ⁰^ ^— dr') ^{— 2 M} 2 ? 3 ■

""I— r

/ dL 2 ₊ d? 2 A _— ik dLU ₊ d? 3 A ₊ \ dr dr )   ^2 \ dr dr )

Let us neglect small components, so we obtain

Br ² + 2 m

-

pair IV

^{+ L +}

d2S д 2--ikM(L0 — ?0) — dr2

— ( M + E ) M ( L 2 + ? 2 ) - 2 M ² ? 2 ;

( M + E ) M ( L з - ? з ) +

( Br ² + 2 m ) M

2V2 r

⁽ L о + ? o ⁾⁺

+

B ² r ⁴ + 4 B ( m — 1) r ² + 4 m ² —

8 r^{1 2}

—⁽ L 1 ⁺ ? i ⁾⁺

+

( Br ² + 2 m ) ik

2V2 r

⁽ L 2 + ? 2 ^{) +}

-

V2 r dL dr

L ₁ + 2 ikL ₂ +

Br ² + 2 m + 2

2^ r

L 3

-

-

2 EL 0 +

—■— ) + 2 ? 0 ( M + E ) — — 2 M? 0 , dr

^{—Br 2 — 2} m ^{+ 2}

-------7=------ ? 1 — 2 ik? 2 —

2 r

Br ² + 2 m + 2

-

-

+

V² r

- 3 ^( d?  dS ?)—“

( Br ² + 2 m ) M

V 2 r

B ² r ⁴ + ( — 8 k ²

? 0 + x 2 MdS ⁰ + dr

— 4 Bm ) r ² — 4( m —

-

B ² r ⁴ + ( — 8 k ² — 4 Bm ) r ² —

8 r ²

^ m t^{1 2} ( L 3 + ? .3 ) —

-

dL ₀ + d?^

-

Br ² + 2 m — 1 2 r

/ L + d? 1 A dr dr

-

+

8 r ²

( Br ² + 2 m ) ik

+-- 7=----- L ₂+

2V2 r

B ² r ⁴ + 4 B ( m + 1) r ² + 4 m ² —

1) ²

L 1 +

-

-

dL 2 + d? 2 dr dr

1 ⁽ d ² L 1 ⁺ 2 r (i r ^ ⁺

( Br ² + 2 m ) M

2/2 r

M

+ x 2

( M + E ) M ( L 3

+

-

+

-

+

8 r ²

— ^L 3 ⁺

) + 1 (d L + d? ) +

)   2 r V dr dr )

1 dL 1     ik dL 2

2 r dr     a/2 dr

Br ² +2 m + 1 dL 3

2 r

dr

+

d ² S 1 dr ²

)+u

d ² L 3 dr ²

d ² S 3

⁺ dr ² )

-

1 d ² L 1 d ² L

⁺ 2 d^  d^ MEL ^{1 -0} ’

( Br ² + 2 m ) M

⁽ L 0 ^- ? 0 )⁺ ( M ⁺ E ) M ⁽ L 3 ⁺ ? 3 ⁾⁺

/ dL o — dS ° A -2 m ² l 3 , dr dr

— ? 3 ) +

( Br ² + 2 m ) M

2V2 r

( L 0 + S 0 )+

B ² r ⁴ + 4 B ( m — 1) r ² + 4 m ² —

8 r ²

( L 1 + S 1 )+

+

( Br ² + 2 m ) ik

2V2 r

( L 2 + S 2 )+

B ² r ⁴ + ( — 8 k ² — 4 Bm ) r ² — 4( m + 1) ²

8 r 2                    ^{( L 3 +} ? ³ ) ^—

dL 0 + d? 0 A dr dr

Br ² + 2 m — 1

-

2 r

/ dL 1 + d? 1 A dr dr

-

V2r r

-

+

-

dL 2 + d? 2 dr dr

₊1   + dh +

)   2 r\dr dr )

1 / d ² L 1    d ² ? Л   1 / d ² L ₃

⁺ 2 \" dr ²" ⁺ " dr ²"/ ⁺ 2 \" dr ²"

( Br ² + 2 m ) M

2^2 r

+                 -

⁽ L 0 ^— ? 0 ) ^{— ( M +} E ) ^{M ( L} 3 ⁺ ? 3 )

-

L 0 + V 2 Mdr — 2( M + E ) MS 1 +

B ² r ⁴ + ( — 8 k ² — 4 Bm ) r ² — 4( m —

+

8 r ²

( Br ² + 2 m ) ik

+--7=----- L 2 +

2V2 r

B ² r ⁴ + 4 B ( m + 1) r ² + 4 m ² —

1) ²

L 1 +

8 r ²

—^L 3 ⁺

1 dL 1     ik dL 2

2 r dr     a/2 dr

Br ² + 2 m + 1 dL 3

2 r

dr

+

+2 dL +1 dL -2 m ²

2 MEL 2 — 2 ikM? 0

-

S 1 ,

( Br ² + 2 m - 2) ik

-

( Br ² + 2 m )

4 r^{1 2}

2 _{L 2}

-

2^2 r

( Br ² + 2 m + 2) ik

2_X 2 r

L 1 ^-

L 3 +

ik dL 1

+ v2 dr

₊ 1 dL 2 r dr

-

ik dL ₃    d ² L ₂ =

^ 2 dr     dr ²     ^’

— 2( M + E ) M? ₂ — 2 ikML ₀ —

( Br ² + 2 m - 2) ik

2V2 r

L ₁

-

-

( Br ² + 2 m )

4 r ²

² L 2

-

( Br ² +2 m + 2) ik

2V2 r

L 3 +

_

ik dL 1    1 dL 2

-72 dr    r dr

-

ik dL

3 +

V2 dr

d ² L 2 dr ²

= 2 M ² S 2 ,

( Br ² + ² m ) M_c      ddS о

----—----S 0 — V 2 M —-— + 2 ML з E + 2 r                 dr

B ² r ⁴ + 4 B ( m — 1) r ² + 4 m ²

⁺             8 r 2

+

( Br ² + 2 m ) ik

------7=----- L 2 +

2_X 2 r

-

L 1 +

+

—B ² r ⁴ + ( — 8 k ²

— 4 Bm ) r ²

8 r ²

— 4( m + 1) ²

L 3 ^-

Br ² + 2 m — 1 dL 1 ik dL 2

2 r      dr   2^ dr

₊ 1 dL 3 ₊ 1 d 2 L 1 ₊ 1 d 2 L 3 = ₀

2 r dr 2 dr ²     2 dr ^{2      1}

4 2 M^ + ⁽ Br 2 ^{+ 2} m ) M L 0 — 2( M + E ) MS 3 + dr           2 r

B ² r ⁴ + 4 B ( m — 1) r ² + 4 m¹²

⁺             8 r 2

_

L 1 +

+

( Br ² + 2 m ) ik

------7=----- L 2 +

2X2 r

+

-B ² r ⁴ + ( - 8 k ²

- 4 Bm ) r ²

8 r ²

— 4( m + 1) ²

L 3 -

Br ² +2 m - 1 dL 1 ik dL 2    1 dL 3

2 r      dr    42 dr   2 r dr

, 1 d ² L 1 , 1 d ² S 1 , 1 d ² L ₃ ⁺ 2 dr ^{2 +} 2 " dr ²" ⁺ 2 dr ²

= 2 M ² S 3 •

We assume that nonrelativistic energy may be neglected in comparison with rest energy M + E к M . Also from equations (1), (4), (6), (8) we express the small variables S 0 , S 1 , S 2 , S 3 and substitute them in equations (2), (3), (5), (7). In this way, we obtain equations which contain only the big components

(- d a + ¹ d- + 2 ME - k² dr ²    r dr

_

( m - 1) ²

r2

_

B2r2

4 Brn \ L 1 = 0 , L 1 = N 1 f 1 ;

( 77 + ¹ d + 2 ME — k ² dr ²    r dr

_

m2 r2

_

B2r2

4 Bmj L 2 = 0 ,

^L 2 = N 2 f 3 ;

( 77 + ¹7" + 2 ME — k ² dr ²    r dr

_

( m + 1) ² r ²

B2r2

4 Bm \ L 3 = ⁰ , L 3 = N 3 f 2 ;

(ds ⁺

¹ d +2 ME - k ² — r dr

m2   B2r2

”2 Bm I L o + r ²      4

+4 (т

2X2 ddr

m + Br ²

_

r

77) L 1 +

+ 4 dT +

242 к dr

m + Br ² / 2 + 1 \ --------------- ^L 3 = ⁰ •

r

The last equation may be re-written differently

(33 + 1 d +2 ME dr2 r dr

- k ²

9m2

r2

B2r2

Bm L 0 +

⁺    /- ⁽ N 1 b m - 1 f 1 ⁺ N 3 a m +1 f 2 ) = ⁰ •

It is evident that L ₀ = constf 3 , then eq. (7) takes on the form

N 1 b m - 1 f 1 + N 3 a m +1 f 2 = 0 •         (8)

There exist differential constraints (see in [1])

bm-1 f1 = C1 f3,  am+1 f2 = C2 f3, they permit us to transform the previous relation to the following form (see [1])

N 1 b m - 1 ^f 1 ⁺ N 3 a m +1 ^f 2 =

= ( N 1 C 1 + N 3 C 2 ) f 3 = 0 ^ N 1 C 1 + N 3 C 2 = 0 •

Thus we have obtained 4 separate equations (only 3 equations are different, their solutions will be found in the next section)

[ 7 7 + ¹ T + 2 ME ~ k¹² dr ²    r dr

B2r2

- Bm

L 1 = 0 ,

( m — 1) ² r ²

L 1 = N 1 f 1 ;

[

d2

d^ + ^{1 d} +2 ME dr ²    r dr

k2

m2 r2

B2r2 - Bm L2 = 0, L 2 = N2 f3; -4 [ db+r d + 2ME - k12 (m + 1)2 -   r2  - dr B2r2 L3 = 0, L 3 = N 3 f2; -4 - Bm [ dL + 1 d +2ME — k2 - m2 - dr2 r dr r2 B2r2 - Bm L0 = 0, L0 = N0f3 ; -4 and the algebraic constraint

N 1 C 1 + N 3 C 2 = 0 .

Recall that (see [1])

C 1 = VX-B, C 2 = V X + b ,

, 1 - (2 a 1 + 1) B + 2 ME - k¹²

⁺ 2            B

-

Bm

F ₁ = 0

X — 2 BN — 2 ME - k ² .         (9)

with parameters

General solution on the nonrelativistic equation consists of three components (the general multiplier e ^imϕ e ^ikz is omitted):

а 1 —

(2 a 1 + 1) B — 2 ME + k ² + Bm

2 B

■ y 1 = ² a 1 ^{+ 1} .

/1\                  /0\

Ф = e ^{-iE 1} t N i I 0 I f i + e - iE ² t N 3 I ^ I f ₂ +

In order to get the bound states a 1 = +|m — 1|, Y1 = m — 1| + 1,

+e-iE3tN2 I 0 I f3 + e—iE3tN0 I 0 I f3(r)• k2 + B(|m - 1| + m + 1) - 2ME

We have 3 different series of energy levels, E 1 , E 2 , E 3 and 3 different wave functions. This result agrees with that obtained in relativistic case.

• 2.    Solving the differential equations

The above three equations let us transform to the variable

x — Br2 /2, B > 0: d2 L1 + 1 dL 1 + dx2   x dx 1 , 12ME - k 2- m 4 + 2        Ba 1 (m - 1)2 ] 4 x2 L1 — 0, (10) d2 L 2 + 1 dL2 + dx2   x dx 1 , 12ME - k 2- m 4'2       Bx 1 m2 4 x2 L2 — 0, (11) d2 L 3 + 1 dL3 + dx2   x dx ' 1 , 12ME - k 2 - Bm 4 + 2        Bx 1 (m + 1)2 ] 4 x2 L3 — 0 • (12) Consider eq. (10): L1 — X a1 eb1 xF1, d2F1                    dF1 x d 2 + (2a 1 + 1 + 2b 1 x) d + Г 1/^,2    \     1 4 a2 - (m - + 4 4b1 - 1) x +4   * x 1)2 + + 18 a 1 b 1B + 4 b 1B + 4ME - 2k2 - 2Bm" B F1 — 0. Imposing restrictions a 1 — ±-|m - 11, b 1 —- 2 we ob- tain the equation of confluent hypergeometric type xdF + (2a 1 + 1 - x)dF1 + dx2

that polynomial condition а 1 — -n 1 gives

• E. - F — B ( n. + m- Ui m ii) . (13)

• 1  2 M   M \ 1        2

Two other equations lead to similar results. Thus, we get

L 1 — x|m-1 |/2F-x/2F(-n 1, |m - 11 + 1 ,x), k2    B |m - 1| + m + 1

• E1 - 2M = MV 1+ !----2

L ₂ — x ^{m/ 2} F ^{-x/ 2} F ( -n ₂ , |m| + 1 , x ) ,

• k ²     B |m| + m + 1

• ^E 2 - 2 M ^— mV 2 ⁺     2---- )■ ⁽¹⁴⁾

L 3 — x ^{|m +1 1/ 2} F ^{-x/ 2} F ( -n 3 , |m + 1 | + 1 , x ) ,

• k ²     B |m + 1 | + m + 1

• ^{E 3 -} 2 M ^— M Г ^{3 +}      2      )•

Discussion

The nonrelativistic wave function for Stuckelberg particle turned out to be 4-dimensional. We have derived the corresponding radial system for 4 functions. It has been solved in terms of confluent hypergeometric functions. There arise three series of energy levels with corresponding solutions. This result agrees with that obtained for the relativistic Stuckelberg equation.

It may be noted that the similar nonrelativistic study for Stuckelberg particle in presence of the external Coulomb field was done in [5]. The energy spectrum was found. Besides, a general Pauli-like equation was derived for this particle in presence of arbitrary electromagnetic field.