Study of liquid metal flow and passive impurity transport driven by a traveling magnetic field in a rectangular cavity

Одной из прикладных проблем, связанных с процессом массопереноса, является гомогенизация сплава в процессе приготовления после добавления в него легирующих компонентов [1, 2]. Скорость гомогенизации жидкого металла, помимо интенсивности течения, определяется и скоростью диффузии вводимых примесей.

Из-за высокой температуры ( T >  700 ° C) и непрозрачности экспериментальные исследования течений и процессов массопереноса в объеме расплавленного металла в настоящее время имеют либо низкую точность, либо очень сложны, в связи с чем эта область еще недостаточно изучена. Появление ЭВМ с высокой вычислительной мощностью и большой оперативной памятью сделало возможным проведение численных экспериментов вместо натурных. При этом для верификации расчетов можно использовать доступные для экспериментального измерения электромагнитные силы, поля скорости течения и магнитной индукции.

В неподвижной жидкости перенос пассивной примеси осуществляется только за счет молекулярной диффузии. Как известно, в равновесных и однородных системах практически все вещества в расплавленном виде имеют приблизительно одинаковый коэффициент диффузии, равный D ® 5 - 10 " ⁴ см²/с [3]. По этой причине, в отсутствие перемешивания, гомогенизация сплава протекает медленно. Равномерное распределение вводимых в сплав легирующих компонентов можно значительно ускорить путем создания вынужденной конвекции, добавляя к молекулярной диффузии еще и конвективный перенос и турбулентную диффузию.

Движение расплава создается либо механическим (механическими мешалками), либо электромагнитным (МГД-перемешивателями) способами. В последнее время в цветной металлургии и литейном производстве в связи с постоянным ростом требований к качеству получаемого материала и развитием прикладных приложений магнитной гидродинамики (МГД) при изготовлении сплавов все большее распространение получают МГД-установки. Такие устройства не требуют замены изнашиваемых деталей и не загрязняют металл, в то время как механические мешалки со временем разрушаются. Кроме того, МГД-перемешивание способствует снижению химической неоднородности заготовки, очищению металла от неметаллических включений и растворенных газов [4].

Из многочисленных исследований известно, что наилучшее перемешивание происходит при турбулентном движении [1]. Однако, несмотря на давнюю историю изготовления сплавов, до сих пор

нельзя дать однозначного ответа на вопрос, какая именно гидродинамика необходима для достижения требуемого качества перемешивания. Как показано в [5], не следует полностью отвергать практическое значение и медленного ламинарного режима для решения отдельных задач. Таким образом, процесс перемешивания по-прежнему остается актуальной проблемой.

Хорошо известными статьями, содержащими результаты экспериментального изучения распределения частиц в турбулентном потоке, являются [6, 7]. Здесь распределение примеси, дающее информацию о динамике гомогенизации сплава, определяется с помощью оптической металлографии срезов застывшего металла. Перенос примеси численно изучался в работах [8–10]. В большом числе публикаций обсуждается перемешивание в цилиндрических полостях [11–15], в то же время перемешивание в полостях другой формы освещено значительно меньше [16].

2.    Постановка задачи

Рассматривается прямоугольная полость с жидким металлом (Рис. 1), где h и l — глубина слоя и его длина вдоль оси x соответственно, по оси z полость вытянута до бесконечности. Снизу полости на некотором расстоянии R ₀ от ее дна через равные промежутки λ параллельно друг другу расположены шесть линейных

Рис. 1. Расчетная область для магнитного поля и объемных сил; градациями серого цвета обозначено распределение магнитного поля, стрелками – поле действующей в проводящей среде средней по времени электромагнитной силы, белыми полукругами – сечения проводников, штриховой линией – область с проводящей средой

бесконечно длинных тонких проводников, ориентированных вдоль оси z . По проводникам течет переменный электрический ток силой I и круговой частотой ω ( ω = 2 πν ). Фазы колебаний электрического тока в соседних проводниках различаются на π/3 , так что магнитное поле, генерируемое электрическими токами в проводниках, создает бегущую вдоль оси x волну .

Возникающее переменное во времени магнитное поле индуцирует в проводящей среде электрические токи, которые, взаимодействуя с ним, порождают объемную силу, способную вызвать движение среды. В реальных условиях скорость течения жидкого металла значительно ниже скорости бегущего магнитного поля. По этой причине обратным влиянием течения жидкого металла на бегущее магнитное поле можно пренебречь. Тем самым электромагнитная и гидродинамическая части задачи расцепляются и могут решаться независимо.

• 2.1.    Электродинамическая часть

Электромагнитные процессы в проводящей среде описываются уравнениями: – Максвелла в низкочастотном приближении

– условием отсутствия магнитных зарядов

– законом Ома

∂ B ∂ t

- rot Ε ,

rot B = µ ₀ j ;

div B = 0;

j = σ E .

В уравнениях (1)–(4) приняты обозначения: B — магнитная индукция; E — напряженность электрического поля; µ0 — магнитная проницаемость вакуума; j — плотность электрического тока;

σ — проводимость среды.

Подставляя Закон Ома (4) в уравнение для закона индукции Фарадея (1), имеем dB

□    = - rot j .

d t

Представим зависимость магнитного поля и тока от времени в виде: B = В _П e* “ ^t и j = j _П e* “ ^t , где В _П, j _П — магнитная индукция и плотность электрического тока не зависят от времени; тогда сократив на e* “ ^t , получим * 'стю В П =- rot j _П.

Возьмем в качестве масштабов: длины — толщину слоя металла h ; магнитного поля — B 0 = ц ₀ I 0 [^ 2 п R 0 ) , величину магнитного поля на нижней границе проводящего слоя, создаваемого током I ₀ одного проводника; плотности тока — j 0 = с® hl _о ц _о /( 2 п R 0 ) . Здесь В _П = B ₀ В _б , j * = j 0 j _Б, где индексом Б обозначены соответствующие безразмерные величины магнитной индукции и плотности тока. Тогда уравнение для нахождения токов, индуцируемых в проводящей среде переменным магнитным полем, станет выглядеть как

* В б =- rot 1 б .

Для нахождения электромагнитных сил в слое металла применялась следующая схема вычислений. Сначала при помощи закона Био-Савара-Лапласа d B = ц ₀ 1 [ r х dr ]/ ( 4 п r ³) отыскивалось магнитное поле, создаваемое внешними линейными токами, без учета действия проводящего слоя металла:

B ( _х , y )    "    i_o V e ⁽ n ^-1)3--------- y ,

^Бх'  ^у’   2 п B 0 ⁰ П : 1        ( x - ( n - 1) Х )² + у²

^B Б у ⁽ x , У ) =

Ц о I у e ^{( n - 1)} 3     x ^{- (} n ^{- 1)} ^

2 п B о ⁰ 1:       ( x - ( n - 1) Х )² + у^2.

На следующем шаге, на основе уравнения (5) и уже вычисленных значений компонент магнитного поля (6), рассчитывались индукционные токи в металле. По их значениям, согласно закону Био–Савара– Лапласа, находилось магнитное поле индуцированных токов во всей области, которое суммировалось

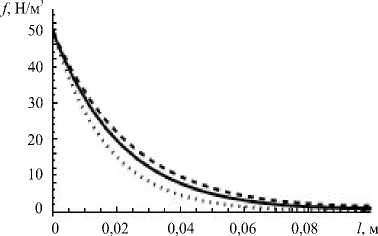
Рис. 2. Зависимость объемной электромагнитной силы от глубины слоя металла для разных частот тока индуктора, Гц: 7 (точки); 50 (пунктирная линия); 100 (сплошная линия)

с исходным. Вычисления повторялись до тех пор, пока разность между двумя итерациями не уменьшалась до заданного значения. После установления магнитного поля и электрических токов с помощью выражения f = j х B определялась объемная электромагнитная сила f в слое металла.

Бегущее магнитное поле создает в металле объемные электромагнитные силы и увлекает его за собой. По мере проникновения переменного магнитного поля вглубь слоя за счет скин-эффекта амплитуда поля затухает по экспоненциальному закону (Рис. 2). Таким образом, электромагнитные силы действуют на жидкий металл неравномерно по глубине слоя, и ротор электромагнитных сил отличен от нуля, что в замкнутой области приводит к возникновению циркуляционного (перемешивающего) течения.

• 2.2.    Верификация

Приведем простейшие соображения, позволяющие заключить, что должна существовать некая частота тока в индукторе, при которой силовое воздействие максимально. Рассмотрим два крайних случая. При постоянном токе в проводниках (нулевой частоте магнитного поля) ток в металле индуцироваться не будет, следовательно, не возникнет объемная сила. При очень же большой частоте переменного тока, питающего индуктор, из-за сильного скин-эффекта электромагнитные силы сосредоточатся в тонком поверхностном слое, что приведет к уменьшению их воздействия на жидкий металл. Значит, максимальное силовое воздействие оказывает ток с частотой, лежащей в промежутке между нулевой частотой и большими ее по значению.

Достоверность электродинамических расчетов была проверена специальным экспериментом. В эксперименте индуктор магнитного поля располагался так, чтобы направление движения бегущего

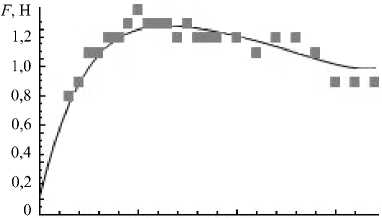
О 50 100 150 v, Гц

Рис. 3. Зависимости силы, интегральной по ширине медного слоя, от частоты бегущего магнитного поля (сила тока в обмотке индуктора 200 А): расчет – сплошная линия; эксперимент – квадратики

магнитного поля было направлено вверх (противоположно силе тяжести). Параллельно индуктору устанавливалась медная пластина, в которой возбуждались электромагнитные силы, также направленные вверх. Изменение веса пластины регистрировалось с помощью цифровых весов с точностью 1 г.

Результаты численных расчетов электромагнитных сил, возникающих в пластине, удовлетворительно совпадают с экспериментом (Рис. 3). Из рисунка видно, что для заданной конфигурации индуктора магнитного поля оптимальная частота, при которой силовое воздействие максимально, соответствует приблизительно 50 Гц.

• 2.3.    Гидродинамическая часть

Гидродинамические процессы в проводящей среде описываются в рассматриваемом случае – уравнением Навье–Стокса

∂ ^V + ( V ∇ ) V =- ¹ ∇ p +ν∆ V + ^f ;

∂t   ρρ

– уравнением неразрывности для несжимаемых сред divV = 0 ;

– уравнением переноса пассивной примеси, добавляемым при исследовании процесса перемешивания

+(V∇)C =D∆C, ∂t где V и ρ — скорость и плотность жидкости, p — давление, ν — кинематическая вязкость, С — концентрация примеси, D — коэффициент диффузии.

Принимая за масштаб длины глубину слоя h , скорости — ν/ h , времени — h ² I ν и учитывая масштабы плотности тока и магнитного поля, введенные выше, вместо уравнений (7)–(9) получим уравнения в безразмерном виде:

∂ ^V + ( V ∇ ) V =-∇ p +∆ V + S ⋅ j Б × B Б ;

∂t divV = 0 ;                                           (10)

∂C+(V∇)C=1 ∆C, ∂t            Sc где S= j0B0h3I(ρv2) = σωµ20h4I02J( 4ρν2π2R02) — введенный авторами данной работы безразмерный параметр, Sc = vD — число Шмидта.

На границах использовались условия прилипания и непротекания. Система уравнений (10) решалась конечно-разностным способом в естественных переменных методом расщепления [17], который состоит в последовательном учете нелинейных членов, вязкости, давления и электромагнитной силы. Сетка имела 500 × 250 узлов, а безразмерные параметры имели следующие значения: S ≈ 3,5 × 10⁷ , Sc ≈ 3,8 × 10² .

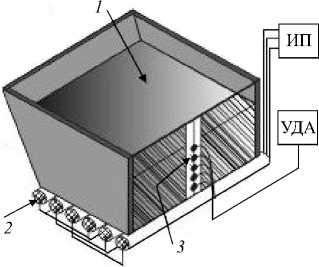
Параметры для численного эксперимента — глубина, ширина слоя жидкого металла, конфигурация индуктора магнитного поля, плотность и проводимость металла — выбирались в соответствии с параметрами экспериментальной модели (Рис. 4). Ванна модели перемешивателя представляла собой

а

Рис. 4. Схема ( а ) и фотография ( б ) экспериментальной установки. 1 – жидкий металл; 2 – медные шины индуктора магнитного поля, 3 – датчики ультразвукового доплеровского анемометра (УДА); ИП – источник питания

б

уменьшенную копию промышленной печи для плавки металла. Рабочим металлом являлся галлиевый сплав (88% Ga, 10% Sn, 2% Zn). Объем ванны с металлом составлял 8 л.

Измерение скорости движения металла проводилось с помощью ультразвукового доплеровского анемометра (УДА). В непрозрачном расплавленном металле нельзя применить оптические методы, такие как лазерная доплеровская анемометрия или Particle Image Velocimetry (PIV), а ультразвуковой доплеровский анемометр позволяет проводить измерения скоростей вплоть до 0,01 мм/с. Пять датчиков УДА располагались со стороны передней прозрачной для ультразвука плексигласовой стенки установки на специальной, перемещаемой по горизонтали планке. Принцип работы УДА основан на том, что датчик испускает ультразвуковую волну определенной частоты, которая отражается от присутствующих в металле микрочастиц. УДА измеряет только одну компоненту скорости — вдоль ультразвукового луча.

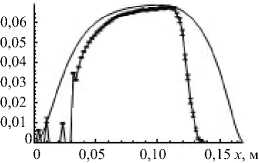
Проведенная серия экспериментов по измерению скорости для разных частот и силы тока в индукторе магнитного поля показала, что результаты эксперимента находятся в качественном согласии с численными расчетами (Рис. 5). Наблюдаемое некоторое расхождение расчета и эксперимента можно объяснить влиянием двух факторов. Во-первых, расчет осуществлен в двумерном приближении, в то время как экспериментальные измерения скорости проводились на трехмерном течении. Во-вторых, в экспериментальной модели задняя стенка ванны имела наклон, что не учитывалось при численной реализации.

а

Г, м/с

К м/с О

-0,01

-0,02

-0,03

-0,04

-0,05

-0,06

-0,07

К, м/с

О -0,01 -0,02 -0,03 -0,04 -0,05 -0,06 -0,07

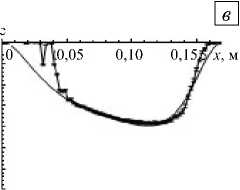
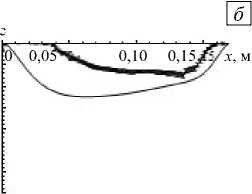
Рис. 5. Профили скорости при v = 30 Гц; 1 ₀ = 200A, полученные экспериментально (жирные точки) и численно (сплошная линия), на различной глубине слоя y , м: 0,01 ( а ); 0,05 ( б ); 0,09 ( в );

Для создания высококачественного сплава важно добиться его гомогенизации. Вместе с тем желательно сократить время перемешивания в целях уменьшения затрат энергии и предотвращения перегрева сплава. Степень гомогенизации сплава предлагаем оценивать с помощью параметра ^ ( t ) — «коэффициента неоднородности»

« t 1 ) =

/^- { ( C - C 1 )² + ( C - C 2 ) 2 + ... + ( C - Cn )² }| n t

I -{(C - C1)2 + (C - C2)2 +... + (C - Cn )2}| nt то есть отношения среднеквадратичного отклонения концентрации примеси C во всех точках n расчетной области от конечной концентрации после идеального перемешивания (в момент времени t1 ) к среднеквадратичному отклонению в начальный момент времени t = 0. Введем также еще один параметр,

б

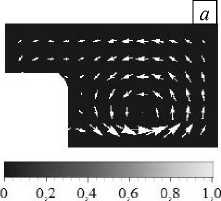
Рис. 6. Эволюция скорости (стрелки) и распределения примеси (градации серого цвета) в слое жидкого металла при перемешивании его бегущим магнитным полем: в начальный момент времени в области, обозначенной белым квадратом, концентрация примеси равняется 1 ( а ); распределение концентрации примеси через 5 с ( б ); через 15 с ( в )

который связывает затраченное на перемешивание время с достигнутой степенью гомогенизации, — это «время перемешивания» — интервал времени, за который ξ уменьшается в 10 раз.

На рисунке 6 представлены картины эволюции поля скорости и распределения примеси; со временем течение выходит на стационарный режим, а примесь увлекается движущейся жидкостью и постепенно размывается.

В численном эксперименте при токе в индукторе 200 А были найдены характерные времена перемешивания для разных частот; на основании этих данных построен график влияния частоты тока на время перемешивания (Рис. 7). На графике наблюдается провал в области низких частот (минимальное время перемешивания) и постепенный выход на постоянное значение в области высоких частот. Если сравнивать графики зависимости интегральной силы (силы, действующей на весь слой) от частоты (Рис. 3) и график зависимости времени перемешивания от частоты (Рис. 7), то видно, что нет однозначного соответствия между оптимальными частотами, то есть максимальная интегральная сила еще не приводит к максимальному перемешиванию. Это можно объяснить тем, что перемешивание обуславливается не только интенсивностью перемешивающей силы, но и ее распределением в слое жидкого металла.

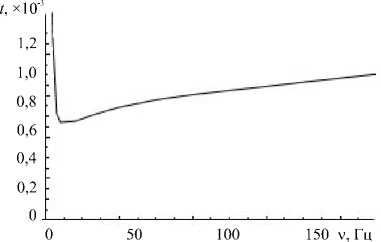
Рис. 7. Зависимость безразмерного времени перемешивания от частоты тока в индукторе магнитного поля

3.    Заключение

Выполненные в работе численные эксперименты показали, что существует зависимость времени перемешивания от частоты тока в индукторе магнитного поля. Максимальную интенсивность перемешивающего течения для заданной толщины и электрической проводимости слоя жидкого металла можно получить, правильно подбирая частоту питающего индуктор тока. Для случая, реализованного в представленном здесь эксперименте, эта частота близка к 5 Гц. Однако разница во времени перемешивания для 5 Гц и 50 Гц не столь существенна и составляет 24%, поэтому для питания индуктора магнитного поля в рассмотренной постановке задачи вполне допустимо использовать ток промышленной частоты как более простой вариант.

Приведенный метод расчета можно использовать для вычисления объемной электромагнитной силы в слое жидкого металла, создаваемой различными конструкциями индукторов бегущего магнитного поля, при условии отсутствия ферромагнитных сердечников.

Работа выполнена при финансовой поддержке Министерства образования и науки Пермского края (соглашение № С-26/251) и РФФИ (проект №12-08-31526-мол_а).