Ступенчатое регулирование внутрибаллистических характеристик ракетного двигателя твердого топлива изменением поверхности горения заряда

Регулирование площади критического сечения сопла ракетного двигателя на твердом топливе (РДТТ) по скорости горения топлива широко применяется при разработке двигателей с целью уменьшения разбросов внутрибаллистических характеристик (ВБХ) двигателя. В работе [1] разработаны основные положения такого типа регулирования, но в ней не учтены корреляционные связи между скоростью горения топлива и температурой заряда и определяются только разбросы ВБХ. В работе [2] приведена детерминированная модель регулирования. В приведенных работах рассматривается регулирование за счет изменения площади критического сечения сопла, однако этот способ неприемлем для малогабаритных двигателей с малым расходом. Диаметр критического сечения сопла у таких изделий составляет всего несколько миллиметров. Выполнение ступенчатого регулирования на таком диаметре с заданной точностью приводит к дополнительным технологическим трудностям. Гораздо проще осуществлять изменение поверхности горения заряда в зависимости от скорости горения топлива при неизменном значении площади критического сечения сопла. Осуществлять изменение поверхности горения можно за счет регулирования длины заряда, тем более, что заряд после прессования подвергается операции обточки торцов. Это значит, что нет необходимости введения дополнительной операции, технологический процесс не усложняется. При регулировании по площади критического сечения при малых его значениях изменение диаметра критического сечения ведет к изменению и самого коэффициента расхода. Это ведет к увеличению разбросов ВБХ и уменьшению параметрической надежности заряда. Данный недостаток исключается при постоянном значении площади критического сечения сопла. В этом случае будет оставаться примерно постоянным коэффициент расхода сопла и будет исключено его влияние на разбросы ВБХ. Регулирование поверхности горения заряда по температуре не рассматривается, так как в практике производства РДТТ в настоящее время оно не применяется.

Зависимость изменения поверхности горения от скорости горения топлива принимаем ли нейной 5S = —5U, где 8S - вариация поверхности горения; ф(U) - функция регулирования, д U                                                   v '

8 U - вариация скорости горения топлива; у - ВБХ двигателя. Здесь и далее используем метод вариаций [1, 3].

Зависимость ВБХ двигателя у = f ( U , T , S ) линеаризуем, считая температуру константой, -   д f _т д f^

а скорость горения топлива и поверхность горения заряда переменными 5 у =--- 5 U +-- 5 S .

ди    дS п                                       Я ( дf , дf дфы

Решая совместно, получаем выражение 5 у =--1---5 U . Используя полученное выраже-

V д U д S д U )

ние, можно определить параметры распределения ВБХ на j-м интервале регулирования. Математическое ожидание будет определяться м^=у+Гf+ l.-^1 [u -u ), v> y   дU дS дU ( j j)

а дисперсия характеристики

D ( у ) =

дf      ,дф д U д S д U

^О Л U j

где о Л U j - дисперсия скорости горения на j- м интервале регулирования. Определим эту дисперсию по схеме, приведенной в работе [4], используя усеченное распределение скорости горения, плотность которого будет определяться

L(U ) = F (Uj)-1 F (Uj _,) f(U ) = ЛFL (U), где F (Uj) - интегральная функция плотности нормированного нормального распределения.

Математическое ожидание скорости горения на j-м интервале м (uj ) = ^F / Uf (и) du = -f(Uj )-f(Uj-1) = -|^, v / ЛF /                 ЛF        ЛF

Uj-i где f (U) - плотность нормального распределения.

Дисперсия скорости горения на j- м интервале

₍ x 1 ^Uj ₍         2 z x                      Л F uf ( U ) 1

D (Uj ) =     I (U — Uj) f (U) dU = 1 - l-f- I -           , v J / ЛF                        V ЛF)      ЛF uj-i где лГUf (и)] = ujL(uj)-uj-if (uj-i).

Определяем средневзвешенную дисперсию по всему интервалу изменения скорости горения:

IL ^{Л F} J D ( ^u j )

D c ( ^U ) =               .

L ЛFj j'=1

где m – количество интервалов регулирования площади критического сечения сопла.

Суммирование ведем на интервале изменения скорости горения, равном 6 среднеквадратич- ным отклонениям распределения скорости горения. Все интервалы скорости горения одинаковы.

После преобразований получаем:

1 m ( Af )

D (U) = 0,9733--V j cV 7          0,9973 £ AF,

( A f , ) ' F

.

Данную зависимость можно аппроксимировать следующим выражением:

D c ( U ) = 2,84 m '8⁹ exp

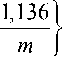
5 = 4,1%.

Полученный вывод сделан для значений скорости горения с исключенной погрешностью замера. С учетом погрешности замера дисперсия скорости будет определяться:

D ( U ) = ° U

A 2

D c ( U ) +      .

° u .

Из графика зависимости Dc (U) = f (m) (рис. 1) видно, что оптимальное количество интер- валов регулирования по поверхности горения составляет от 3 до 8, так же как и для регулирования по площади критического сечения сопла [4].

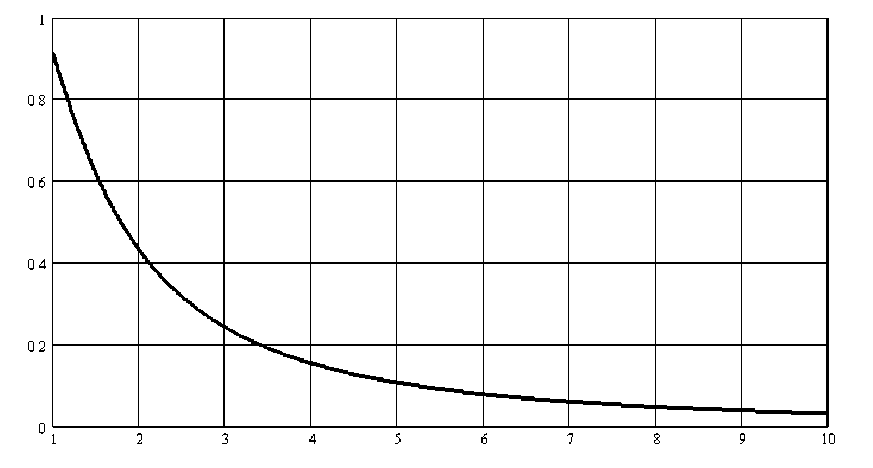
Рис. 1. Зависимость разбросов ВБХ от количества интервалов регулирования поверхности горения

Из анализа полученных результатов можно сделать вывод о том, что при нормальном законе распределения скорости горения и равномерном разбиении интервала регулирования с увеличением числа интервалов разбиения дисперсия скорости горения резко уменьшается и после значения m = 6 практически стабилизируется.

При обработке экспериментальных данных с помощью многомерных распределений можно сразу определить коэффициент уравнения регрессии, который будет связан с теоретическим значением следующим образом:

_ д U d 5 d U _

Из последнего выражения по величине коэффициента Dc (U) можно определить действи- тельный вклад регулирования в снижение разбросов ВБХ.

Оптимизация регулирования, т. е. обеспечение постоянства какой-либо ВБХ, применяется

_  .                                   55 _5 U условие постоянства какой-

довольно часто [1]. Принимая условие регулирования 5 = Сц" > либо ВБХ можно записать:

3 у = ^f f + —C )3 U .

Vд U д s )

Определяем производные ВБХ по величине поверхности горения заряда:

д р d s"

дJp ds

1 P д R_ 1 R ₀ дт = v т д J 1 = 1 PZ 2

1-v s ’ as " 1-v s’ дs" 1 -v s ’ дs - 1 -v ps ’ где Р - давление в камере сгорания, R - сила тяги двигателя, т - время работы двигателя, J[ -единичный импульс реактивной силы, Jp - полный импульс силы тяги, Р - удельный импульс давления, Z2 - уширение сопла, G - расход продуктов сгорания, v - показатель степени в законе горения топлива.

Решая уравнение регулирования, получим значения константы С, при которой будет обеспечено постоянство давления в двигателе; силы тяги; единичного импульса силы тяги; времени вы хода на режим и спада (С = 1); времени работы двигателя и расхода продуктов сгорания (C = —);

1 F„ полного импульса силы тяги C =--2. Полученные константы полностью совпадают со зна-1 -v R чениями, полученными в работе [1]. Однако, используя эти соотношения, можно минимизировать дисперсию только какой-либо одной группы параметров при увеличении остальных разбросов. Наименьшее влияние оказывает регулирование на разброс полного импульса. Остальные параметры образуют две группы с коэффициентами регулирования C = 1, C = —. Поставим цель -найти условие минимального разброса параметров для этих двух групп. Для этого приравняем друг другу квадраты коэффициентов вариации для параметров этих двух групп. Для определенности возьмем давление в камере сгорания и время работы двигателя:

U 1 2 f U 1 ²

• ¹    -^e s^ s j ^_ I^{1 -—в} s^ s ]

  .

  
  

После преобразований получим условие регулирования: C = ^ . При выполнении этого 1+v условия относительные разбросы давления в камере двигателя и его времени работы будут одинаковы. Тот же вывод можно сделать и для других ВБХ. Именно при выполнении этого условия конструкция двигателя будет наиболее близка к оптимальной, а параметрическая надежность его -максимальной. В отличие от условий, изложенных в работе [1], которые обеспечивают независимость какой-либо ВБХ от скорости горения, полученное в данной работе условие обеспечивает получение таких зависимостей ВБХ от скорости горения, которые делают все разбросы примерно одинаковыми.

Расчет параметров распределения ВБХ при регулировании по поверхности горения в линейном приближении можно вести по следующим формулам:

M(y )= у + f N+ C Эф 13 U +N3 T ,

• ^V)     Vд U   д s )    д T

• 2                            2

D ( y ) = ^f J' C 3?) D ( U ) D c ( U ) + С д?^ D ( T ) +

V д U    д s ]                V д T ]

+^{2 г} С X + C 5? 15?) V ^D ( U ) D c ( U ) ^D ( T ) + ^D 0 ( y ) ■

V д U    д s /v д T ]

где Т - температура заряда, r - коэффициент корреляции между скоростью горения топлива и температурой заряда, Do (у) - дисперсия случайных отклонений внутрибаллистического пара- метра (при экспериментальном определении это остаточная дисперсия соответствующего параметра)

Зависимости безразмерных ВБХ от величины безразмерной скорости горения при различных видах регулирования приведены на рис. 2–4.

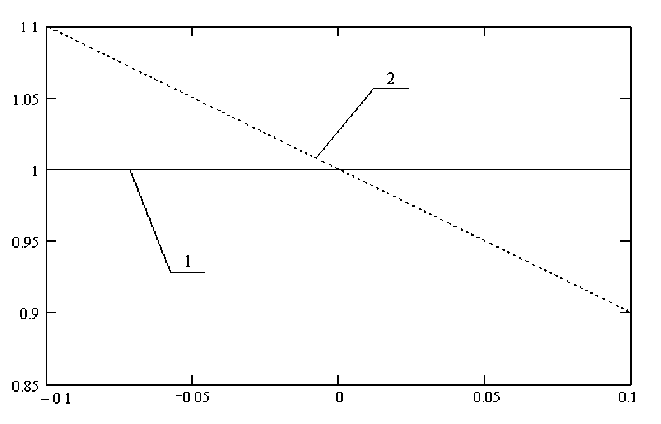
Рис. 2. Зависимости для способа регулирования, обеспечивающего постоянство давления в камере сгорания: 1 – зависимость безразмерного давления

P = 1 ; 2 – зависимость

в

δ U τ= 1 -

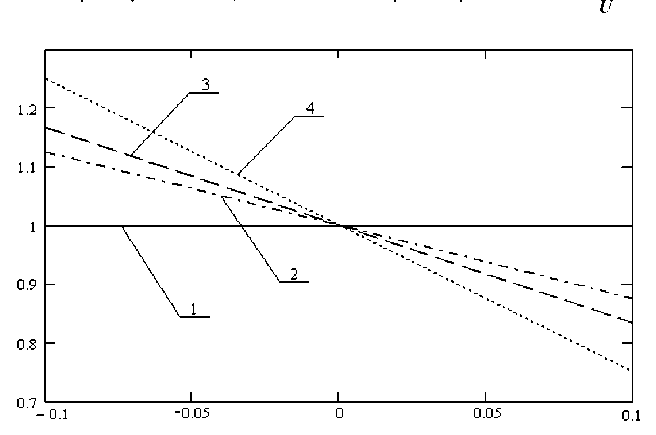
Рис. 3. Зависимости для способа регулирования, обеспечивающего постоянство 1 δU                    1 δU времени работы: 1 - т = 1; 2 - P = 1---, v = 0,8; 3 - P = 1---, v = 0,6;

ν U                ν U

4 - P = 1 - 1 U _; v = 0,4

ν U

Величина _U есть межпартионный разброс скорости горения, т. е. ± 0,1.

Анализ формулы для определения дисперсий ВБХ показывает, что при регулировании, исходя из условия обеспечения постоянства давления в камере сгорания, разбросы давления в камере будут минимальны (примерно равны случайным отклонения давления), разбросы времени работы будут примерно равны межпартионным отклонениям скорости горения. При регулировании, исходя из условия обеспечения постоянства времени работы, разбросы времени работы будут минимальны, но разбросы давления в камере возрастут в ν раз относительно величины отклонений скорости горения. Регулирование, исходя из условия минимизации отклонений, даст возможность получить одинаковые величины разбросов давления и времени работы, равные от значения отклонений скорости горения топлива. Таким образом, за счет достаточно про-1+v стого изменения вида регулирования можно добиться существенного увеличения параметрической надежности двигателя.

Следует отметить, что дальнейшее уменьшение разбросов при регулировании можно получить путем применения нелинейных зависимостей S = f ( U ) и неравномерного разбиения интервала регулирования.

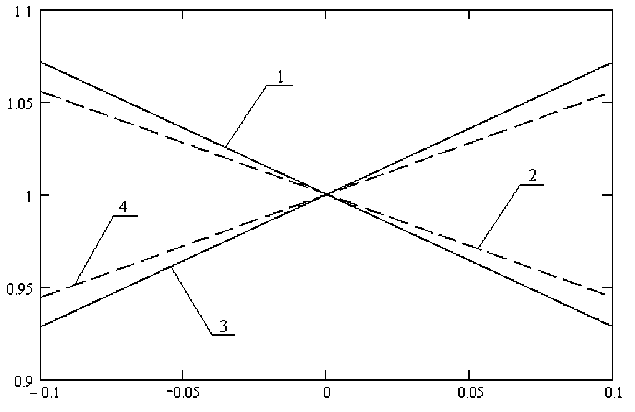
Рис. 4. Зависимости для способа регулирования, обеспечивающего минимум отклонений ВБХ: 1 –

1 8 U

1 + v U v = 0,4; 2 - P = 1 -

1 8 U

1 + v U

P = 1 -

v = 0,8;

3 - T = 1 + — S U , v - 0,4; 4 - T = 1 + — " ' , v - 0,8 1 + v U                  1 + v U

Для малогабаритных РДТТ применяются главным образом заряды трубчатой формы. Величину разбросов поверхности горения для этой формы можно определить по следующей формуле:

D (S )=

L + 2

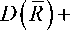
r (L—2) _

D ( r ) +

L

1 — r + L

D ( ^L ) .

Величины поверхности горения S , наружного R и внутреннего r , а также длины заряда L взяты в безразмерном виде, т. е. их величины отнесены к размеру наружного диаметра заряда. При отсутствии непосредственных замеров геометрических размеров заряда можно использовать чертежные значения. Величина среднеквадратического отклонения будет примерно равна 1/6 поля допуска соответствующего размера.

Вывод

Разработанная модель регулирования разбросов ВБХ путем изменения поверхности горения заряда позволяет повысить параметрическую надежность РДТТ и снизить трудоемкость его изготовления.