Существование инвариантных подпространств и экспоненциальных дихотомий решений динамических уравнений соболевского типа в квазибанаховых пространствах

Пусть U , F – банаховы пространства, обозначим L , M ∈ L ( U ; F ) (т.е. линейны и непрерывны). Рассмотрим линейное уравнение соболевского типа

Lu ɺ = Mu .                                         (1)

Вектор-функцию u ∈ C ^∞ ( R ; U ) , удовлетворяющую уравнению (1), назовем его решением . Множество D ⊂ U назовем фазовым пространством уравнения (1), если, во-первых, любое решение u = u ( t ) лежит в D поточечно (т.е. u ( t ) ∈ D при всех t ∈ R ), а во-вторых, при любом u ₀ ∈ D существует единственное решение задачи Коши

u (0) = u ₀                                            (2)

для уравнения (1). Заметим, что если существует оператор L ₁ ^{- 1} ∈ L ( F ; U ) , то фазовым пространством уравнения (1) служит все пространство U . В случае же необратимости оператора L фазовое пространство D может быть подпространством в U .

Далее, пусть оператор M ( L , p )-ограничен, p ∈ {0} ∪ N (т.е. L -спектр оператора M ограничен, а точка ∞ является либо устранимой особой точкой ( p = 0), либо полюсом порядка p ∈ N L -резольвенты оператора M ). В этом случае фазовое пространство D уравнения (1) либо совпадает с пространством U , либо является подпространством в U [1]. Если вдобавок

σ ^L ( M ) ∩ iR = Ø, то фазовое пространство то фазовое пространство расщепляется в прямую сумму инвариантных относительно уравнения (1) пространств: D = J ^s ⊕ J^u , причем u ( t ) ≤ C_s u ₀ e ^{- at} , если a ∈ R ₊ , u ₀ ∈ J^s , t ∈ R ₊ , и u ( t ) ≥ C_u u ₀ e^at , если a ∈ R ₊ , u ₀ ∈ J^u , t ∈ R ₊ , для любых решений задачи (1), (2). Такое поведение решений задачи (1), (2) было названо в [2] экспоненциальной дихотомией. К настоящему времени дихотомии решений линейных уравнений соболевского типа как динамических (т.е. тех, чьи решения существуют на всей оси R ), так и эволюционных (их решения существуют только на полуоси R ₊ ) полностью изучены в банаховых пространствах [3]. Настало время распространить эту теорию на квазибанаховы пространства. Причем нами руководит не столько желание пополнить теорию, сколько стремление к осмыслению неклассических моделей математической физики [4] в квазисоболевых пространствах [5].

Заметим еще, что хотя уравнения вида (1) изучать начал еще А. Пуанкаре в конце позапрошлого века, их систематическое изучение началось с работ С.Л. Соболева во второй половине прошлого века (см. прекрасный исторический обзор в [6]). Термин «уравнения соболевского типа» ввел в обиход Р. Шоуолтер [7]. В настоящее время уравнения соболевского типа привлекают внимание все большего числа исследователей, и аспекты, в которых они изучаются, весьма разнообразны [8–10].

Статья содержит две части. В первой вводятся необходимые понятия и приводится доказательство относительно спектральной теоремы в квазибанаховых пространствах. Во второй – доказывается существование инвариантных пространств и экспоненциальных дихотомий решений уравнения (1) в квазибанаховых пространствах при условии ( L , p )-ограниченности оператора M . Список литературы не претендует на полноту и отражает лишь вкусы и пристрастия авторов.

Относительно спектральная теорема в квазибанаховых пространствах

Пусть U – линеал над полем R . Упорядоченная пара ( U , _U ⋅ ) называется квазинормиро-ванным пространством , если функция _U ⋅ : U → R удовлетворяет следующим условиям:

• (i)    _U u ≥ 0 при всех u ∈ U , причем _U u = 0 точно тогда, когда u = 0 , где 0 – нуль линеала U ;

• (ii)    _U α u = | α | _U u при всех u ∈ U , ∀ α ∈ R ;

• (iii)    _U u + v ≤ C ( _U u + _U v ) при всех u , v ∈ U , где константа C ≥ 1 .

Функция _U ⋅ со свойствами (i)–(iii) называется квазинормой . Ясно, что в случае C = 1 эта функция будет нормой.

Квазинормированные пространства нормируемы только в случае C = 1 , но в любом случае они метризуемы [11, гл. 3]. Значит, в них мы располагаем понятиями фундаментальной последовательности и полноты. Полное квазинормированное пространство называется квазибанаховым . Широко известным примером квазибанахова пространства служит пространство последователь- 1

ностей, ℓ _q при q ∈ (0,1) , константа C = 2 ^q (при q ∈ [1, +∞ ) пространство ℓ _q – банахово). Кроме того, в [5] построены так называемые квазисоболевы пространства ℓ ^m _q при всех m ∈ R , q ∈ R ₊ , причем ℓ ⁰ _q = ℓ _q .

Далее, пусть ( U , _U ⋅ ) и ( F , _F ⋅ ) – квазибанаховы пространства. Линейный оператор L : U → F назовем непрерывным , если lim Lu_k = L ( lim u_k ) для любой последовательности k →∞        k →∞

{ u_k } ⊂ U сходящейся в U , и ограниченным, если при любом u ∈ U справедливо _F Lu ≤ K _U u и K ∈ R ₊ не зависит от u . Нетрудно показать, что линейный оператор L : U → F с областью определения domL = U непрерывен точно тогда, когда он ограничен (т.е. отображает ограниченные множества в ограниченные).

Линеал L ( U ; F ) линейных ограниченных операторов – квазибанахово пространство с квазинормой

Математика

L ( и ; F )lI L II = ^su P f\\^Lu\ I- u H hl

Пример. [12] Пусть {Ak} c R+ - монотонная последовательность такая, что lim Ak = +^, а k→∞ q e R +. В квазисоболевых пространствах m ℓq

= < u

~ ( JU    Л q

= ^{u k ^{} c R} : E l ^A k \ uk¹ 1 k =A        )

< +^ >

рассмотрим квазиоператор Лапласа Л: IЦ+2 ^ IЦ, заданный с помощью формулы Лu = {Akuk}, u e IU. Этот оператор Л: I mm+2 ^ IЦ является линейным, ограниченным и непрерывно обрати мым при всех m e R, q e R+.

Замечание 1. В примере приведено построение оператора в квазибанаховых пространствах последовательностей в явном виде. Соответственно в квазибанаховых пространствах последовательностей (а именно в квазисоболевых пространствах) существуют линейные отображения отличные от нулевого и тривиального, что в функциональных квазибанаховых пространствах не всегда очевидно, а иногда и просто неверно [13].

Замечание 2. В дальнейших рассуждениях пространства U , F - квазисоболевы.

Теперь, пусть операторы L , M e L (U ; F ), введем в рассмотрение L - резольвентное множество p L ( M ) = { pe C :( p L - M ) ^{- 1} e L ( F ; U ) } и L - спектр o L ( M ) = C \ p ^L ( M ) оператора M . В работе [14] показано, что множество p^L ( M ) всегда открыто, поэтому L -спектр o^L ( M ) оператора M всегда замкнут.

Операторнозначные функции комплексного переменного p e p ^L ( M ) c С вида ( p L - M ) ^{- 1},

R p ( M ) = ( p L - M ) ¹ L и L L ( M ) = L( p L - M ) ¹ назовем соответственно L - резольвентой, правой L -резольвентой и левой L -резольвентой оператора M .

Лемма 1. [14] Пусть L, M e L (U; F), тогда L-резольвента, правая и левая L-резольвенты оператора M аналитичны в pL (M).

Введем в рассмотрение условие пусть oL(M) = 7L(M)uoL(M) и of(M)непусто, причем существует ограниченная область Q1 c С

с границей класса С¹, что Q ₁ о 7 L ( M ) и Q 1 n 7 L ( M ) пусто .

При выполнении этого условия, в силу леммы 1, а также результатов из [15] ясно, что существуют операторы, заданные с помощью интегралов

P =    J R P ( M ) d p и Q 1 =    j L p ( M ) d p ,

2 П                 2 n i

Y 1                                     Y 1

где Y ₁ = dQ ₁. По построению операторы P ₁ e L (U ) и Q ₁ e L ( F ).

Лемма 2. Пусть L , M e L (U ; F ) и выполнено условие (3), тогда операторы P ₁ e L (U ) и Q ₁ e L ( F ) являются проекторами в соответствующих пространствах.

Доказательство. Операторы P1 e L (U) и Q1 e L (F) по построению. Для доказательства ут верждения теоремы надо показать идемпотентность этих операторов.

Из условия (3) и замкнутости a^L ( M ) следует существование замкнутого контура у ¹ c C , такого, что a^L ( M ) n у ¹ = 0 и ограничивающего область, содержащую контур у ₁ . Из аналитичности резольвенты R pL ( M ) следует, что оператор

P 1 = 21 i 1 R a ( M ) d A .

ⁿ Y

Используя аналоги тождеств Гильберта [16] и теорему о вычетах, которая справедлива в силу

[15], нетрудно показать, что

P 2

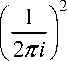
J J R. X ( M ) R g ( M ) d g d X

Y 1 Y

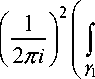
d λ λ - µ

J R g ( M ) d g + J R X ( M ) d X j

Y             Y i            Y

dg

X - g ^

= P i .

Здесь g e Y лежит внутри области, ограниченной контуром у1, а точка Xe у1 находится вне об ласти, ограниченной контуром Y.

Утверждение относительно Q 1 доказывается аналогично. Лемма доказана.

Положим U11 = imP1, F11 = imQ1, U10 = ker P1, F10 = ker Q1; и через L11 (M 11) обозначим сужение оператора L ( M ) на U11.

Теорема 1. Пусть выполнены условия леммы 2. Тогда

• (i)    операторы L 11 , M 11 e L (U 1 ¹; F 1 ¹) ;

• (ii)    существует оператор L -1 e L ( F ¹ 1 ; U ¹¹).

Доказательство. Утверждение (i) следует из построения операторов P1 e L (U) и Q1 e L (F), так как LP1 = Q1 L = L11 и MP1 = Q1 M = M 11.

Утверждение (ii) следует из леммы 1 в силу того, что оператор L -1 равен сужению на подпространство F оператора

^[( g L - M ) ^{- 1} d g .

2 n i^J

Y 1

Теорема доказана.

Наконец, рассмотрим случай, когда существует ограниченная область Q с С , содержащая весь L -спектр c r ^L ( M ) оператора M . По аналогии с банаховым [1] в этом случае оператор M называется ( L, а )- ограниченным . По лемме 2 (в которой c r L ( M ) = 0) существуют проекторы

P =    J R ( M ) d g и Q =    f L L ( M ) d g ,

Ш v                2П1 v

γγ где у с pL (M) - замкнутый контур, ограничивающий область, содержащую область Q.

Следствие 1. Пусть выполнены условия леммы 2 и оператор M ( L, о ) -ограничен. Тогда P 1 = PP 1 = рP и Q 1 = QQ 1 = QQ.

Построим операторы P ₂ = P - P 1 и Q ₂ = Q - Q 1 . В силу следствия 1 эти операторы являются проекторами. Положим U ⁰ = ker P , U ¹ = imP , F ⁰ = ker Q , F ¹ = imQ ; U ¹² = imP₂ , F ¹² = imQ ₂ и через L 1 ₂ ( M ₁₂) обозначим сужение оператора L ( M ) на U ¹² .

Следствие 2. Пусть выполнены условия следствия 1. Тогда

• (i)    U = U ⁰ © U 1 , F = F ⁰ © F 1 , U ¹ = U ¹¹ © U ¹², F ¹ = F ¹¹ © F ¹² ;

• (ii)    операторы L₂,M ₁₂ e L (U ¹²; F ¹²);

• (iii)    существует оператор L -2 e L ( F ¹²; U ¹²).

Инвариантные пространства и экспоненциальные дихотомии решений

Пусть U и F - квазибанаховы пространства, операторы L , M e L ( U ; F ). Рассмотрим линейное уравнение соболевского типа (1). Вектор-функцию u e C ” ( R ; U ) назовем ( классическим ) решением уравнения (1), если она (поточечно) удовлетворяет этому уравнению. Решение u = u ( t ) уравнения (1) назовем решением задачи Коши (2) для уравнения (1) (коротко, задачи (1), (2)), если оно вдобавок удовлетворяет условию Коши (2) при некотором u ₀ e U .

Отображение V • e C ( R ; L (U )) назовем группой операторов , если

V ^ V t = V$ + t                                           (4)

Математика

при всех t,5 е R. Следуя традиции (см. напр. [1]), отождествим группу с ее графиком {V1 : tе R} и назовем ее голоморфной, если она аналитически продолжима во всю комплексную плоскость с сохранением свойства (4). Далее группу { Vt: tе r} назовем вырожденной, если ker V0 Ф {0} (в силу (4) единица V0 группы {v1: t е R} является проектором в U). Наконец, назовем {v1: t е R} разрешающей группой уравнения (1), если вектор-функция u(t) = V‘u0 является решением уравнения (1).

Теорема 2. [16] Пусть оператор M ( L, G ) -ограничен. Тогда существует голоморфнаяраз-решающая группа уравнения (1).

Искомая группа может быть задана, например [15], интегралом

V t = —J R p ( M ) e ^ d p , t е R ,                          (5)

Y где контур у c pL (M) c C такой же, как выше.

Группа (5) не единственная голоморфная разрешающая группа уравнения (1), что легко увидеть, заменив контур у в интеграле, например на контур у 1 . Однако, она обязательно вырождена, если ker L Ф { 0 }.

Для решения вопроса о единственности группы (5) введем несколько понятий.

Определение 1. Множество D c U называется фазовым пространством уравнения (1), если

• (i)    любое решение u = u ( t ) уравнения (1) лежит в D поточечно (то есть u ( t ) е D при всех t е R );

• (ii)    при любом u ₀ е D существует единственное решение задачи (1), (2).

Далее, пусть {vt : tе R} - голоморфная группа, введем в рассмотрение ее образ imU• = imU0 . Ввиду голоморфности группы (5) имеем imU• = imU при всех tе R . Очевидно, образ группы (5) - первый кандидат на роль фазового пространства уравнения (1). Найдем условия, когда эти множества совпадают. Обозначим через L0 (M0) сужение оператора L (M ) на U0.

Теорема 3. [16] Пусть оператор M (L, о )-ограничен, тогда L ₀, M ₀ е L (U ⁰; F ⁰) , причем существует оператор M ₀ ¹ е L ( F ⁰; U ⁰) .

Определение 2. Построим оператор H = M ₀ ¹ L ₀ е L (U ⁰). Назовем ( L, с )-ограниченный оператор M ( L , p )- ограниченным , p е N , если H p ФО и H p + ¹ =О . Присовокупим сюда случай ( L ,0 )-ограниченного оператора M , т.е. случай когда ker L = U ⁰ .

Теорема 4. [16] Пусть оператор M ( L , p ) -ограничен, p е {0} и N. Тогда образ группы (5) совпадает с фазовым пространством уравнения (1).

Определение 3. Пусть D - фазовое пространство уравнения (1), подмножество J c D называется инвариантным пространством уравнения (1), если при любом u ₀ е J решение u = u ( t ) задачи (1), (2) лежит в J поточечно (т.е. u ( t ) е J при всех t е R ).

Теорема 5. Пусть оператор M (L , p)-ограничен, p е {0} и N и выполнено условие (3). Тогда образ группы

• V¹ = — R p ( M ) e ^p d p , t е R ,                             (6)

2 n i    ^p

Y 1

будет инвариантным пространством уравнения (1).

Доказательство следует из равенства imU • = imP 1 = U ¹¹, которое в свою очередь очевидно следует из теоремы 2 и следствий 1, 2.

Определение 4. Будем говорить, что решения уравнения (1) имеют экспоненциальную дихотомию , если

• (i)    фазовое пространство уравнения (1) представимо в виде D = J ¹ ⊕ J ² , где J ¹⁽²⁾ – инвариантное пространство уравнения (1);

• (ii)    для любого u ₀ ∈ J ¹ ( u ₀ ∈ J ² ) решение u = u ( t ) задачи (1), (2) таково, что _U u ( t ) ≤ C ₁( u ₀) e ^{- at} ( _U u ( t ) ≥ C ₂( u ₀) e ^at ) при некотором a >  0 и всех t ∈ R .

Теорема 6. Пусть оператор M (L , p)-ограничен, p ∈ {0} ∪ N и выполнено условие

σ ^L ( M ) ∩ iR = Ø                                 (7)

Тогда решения уравнения (1) имеют экспоненциальную дихотомию.

Идея доказательства этой теоремы основана на построении оценок решений в зависимости от расположения компонент относительного L -спектра оператора M . Опираясь на результаты относительно спектральной теоремы в квазибанаховых пространствах [3], по аналогии с результатами [4,5] можно получить указанные оценки.

Заметим, что если при выполнении (7) окажется, что σ 2 ^L ( M ) = Ø, то J ¹ = imV ^• , где imV ^• – фазовое пространство уравнения (1). В этом случае решения уравнения (1) уместно назвать экспоненциально асимптотически устойчивыми .

Авторы считают своим приятным долгом выразить искреннюю благодарность профессору Г.А. Свиридюку за плодотворные дискуссии и интерес, проявленный к данной работе.