Существование колебательных режимов динамических систем, описываемых обыкновенными дифференциальными уравнениями



СУЩЕСТВОВАНИЕ КОЛЕБАТЕЛЬНЫХ РЕЖИМОВ ДИНАМИЧЕСКИХ СИСТЕМ, ОПИСЫВАЕМЫХ ОБЫКНОВЕННЫМИ ДИФФЕРЕНЦИАЛЬНЫМИ УРАВНЕНИЯМИ*

О. В. Дружинина, С. Н. Петрова

Описан геометрический подход к нахождению колебательных режимов, возникающих в динамических системах, описываемых обыкновенными многомерными дифференциальными уравнениями. Установленная теорема о существовании колебательного режима базируется на использовании функций Ляпунова-Немыцкого.

Рассматривается динамическая система, описываемая обыкновенным дифференциальным векторным уравнением

^ = 5(х),хСЯ", (1)

где правые части системы (1) определены на некотором торовидном теле и в его окрестности, а также удовлетворяют условиям суще-ствования решений и их единственности.

Вопросы существования колебательных режимов различных типов рассматривались в [1—8] и др. В настоящей статье обобщены, уточнены и дополнены результаты В. В. Немыцкого [6-7].

Опишем геометрический подход к нахождению колебательных режимов для случая п = 3. Пусть задана некоторая фазовая траектория q = f(p,t) дифференциальной системы (1) для случая п = 3.

Будем говорить, что фазовая траектория определяет колебательный режим, если существует ось, вокруг которой происходят колебания, т. е. существует прямая L, по отношению к которой осуществимо следующее геометрическое построение. Пусть С - единичный крут с центром на L, расположенный в ортогональной к L плоскости П.

Пусть q = f(p,t) " некоторая точка траектории; проектируем ее на плоскость круга С, и пусть ее проекция q*", тогда проводим радиус-вектор точки q* и отмечаем на единичном круге точку пересечения этого радиус-вектора с кругом С, пусть это будет точка г.

Рассмотрим отображение Tq = г. Изменив t, получим Т (/(p,t)) = r(t).

Пусть t —> сю. Функцию /(р, t) назовем соответствующей колебательному режиму, если степень отображения Т на круг С стремится к оо при t —> со, т. е. точка r(t) бесчисленное множество раз обойдет круг при t —> оо. Для того чтобы аналитически задать колебательный режим,поступим следующим образом.

Пусть дана траектория q = /(р, t) и ось L, Осуществим сначала описанное выше построение для точки р. Выберем в плоскости П некоторую систему координат, и обозначим угол между радиус-вектором точки р* и т-осью через <р. Угол <р назовем фазой колебания относительно оси L и выбранной системы координат. Спроектируем теперь точку q* на у-ось и обозначим проекцию через у*'. Если обозначить расстояние точки q* от начала координат через г*, а угол между радиус-вектором точки q* и направлением <р через а, то имеем

VW = r*(/) sin(a(t) + у).      (2)

Запишем равенство (2) в виде

VW = r*(t)sin

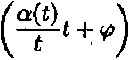
или у* (t) = т * (t) sin WW * + Фр) •

‘Работа частично поддержана РФФИ (проект № 10-08-008Й6-а) и Фондом содействия отечественной науке.

В выражении (3) величина maxr*(t) при

О < t < оо есть амплитуда колебания; а a(t)

выражение w(t) = —есть переменная ча стота. Чтобы от переменной частоты пе в окрестности L, за исключением, быть может, самой оси L, т. е.

d.V d Fi

Ж = ai”^ = рейти к некоторым числовым характеристикам частоты, целесообразно рассматривать born sup u(t) - верхнюю правую частоту колебания и born inf w(t) - нижнюю правую ча

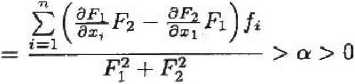
стоту.

Если рассматривать и отрицательное направление времени, то будем говорить и о верхней левой частоте, и нижней левой частоте. Очевидно, все эти величины не зависят от фазы, но зависят от выбора оси L.

Вместо рассмотрения абсолютной амплитуды supr*(t) целесообразнее рассматривать

предел

lim supr(f) = го. t—»оо

Для (4) возможны следующие случаи. Если го = О, то колебания назовем затухающими, если г» — оо, то будем говорить, что имеем дело со случаем внутреннего резонанса, и наконец, если го конечно и отлично от нуля, то будем говорить, что имеются незатухающие автоколебания, или что /(р, t) есть автоколебательный режим.

Рассмотрим аналитический признак существования колебательных режимов. В [6-8] предложен следующий подход. Пусть дана некоторая ось L и задана связка поверхностей, пересекающихся по L, не имеющих других точек пересечения. Предположим, что эти плоскости заполняют цилиндрическую окрестность оси L. Эту связку поверхностей будем задавать уравнением

^(xi,^, ...,хп) =

= arctg

7д(х1де2 ^(льхг

..., Tn ) .-,Xn)

= V,

где ер изменяется от 0 до 2тг.

Функцию V будем называть функцией Ляпупова-Немыцкого относительно оси L и дифференциальной системы (1), если:

• 1)    семейство (5) состоит из непрерывных поверхностей, проходящих через ось L и более нигде не пересекающихся, и через каждую точку цилиндрической окрестности оси L проходит одна и только одна поверхность семейства;

• 2)    производная функции V в силу системы (1) непрерывна и не обращается в пуль

Справедлива следующая теорема.

Теорема. Пусть в некоторой цилиндрической окрестности U оси L существует функция Ляпупова-Немыцкого для дифференциальной системы (1). Тогда в окрестности U существует колебательный реж.им дифференциальной системы.

Пусть выполнено условие теоремы. Тогда имеем

V(t) = V₀+f J at to

Следовательно, если вдоль решения

> а > 0, то V(t) > Vb + a(t — to^ at и функция V(t) неограниченно возрастает вдоль решения, т. е. бесчисленное множество раз угловой параметр у принимает все значения от 0 до 2тт. Теорема доказана.

Следует отметить, что если существует функция Ляпунова—Немыцкого, то все режимы, начальные точки которых находятся в окрестности U оси L, будут колебательными. Из этого факта следует, что теорема 1 необратима.

Охарактеризуем затухающие колебания и автоколебания. Для этого рассмотрим вторую функцию Ляпупова-Немыцкого. А именно, рассмотрим цилиндрическую функцию Ляпунова—Немыцкого, т. е. семейство цилиндрических поверхностей с осью, совпадающей с осью L. Пусть уравнение таких поверхностей Wi(xi,i2, ...,я:п) = С. Если хотя бы на одной из этих поверхностей, расположенных в цилиндрической окрестности U, выполня-dWi о ется неравенство ■■ •• - > 0, то затухания колебаний не будет, а если выполняется нера-венство —■— < 0, то не будет внутреннего резонанса. Вдоль найденных автоколебаний координаты фазовой точки могут по модулю неограниченно возрастать. Если потребовать, чтобы вдоль фазовой траектории координаты оставались ограниченными, то можно использовать параболическую функцию ЛяПуНОВа-НеМЫЦКОГО И^Х^Хг,-.,,#,,) = С,

т. е. такую функцию, поверхности уровня которой пересекают ось L в одной точке и го-меоморфны плоскости. Если среди поверхностей уровня Wz = С найдутся две такие поверхности W^ = Ci и W^ = Сз, и если выполняются неравенства

М\ dt )

<0 и

Сз

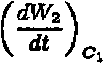
> 0, Ся > Ci,

то в области действия всех трех функций существуют автоколебания с ограниченными координатами как при t —> оо, так и при t —> —оа. Важно отметить, что если доказано существование автоколебаний с помощью трех функций Лянумова-НемьЕЦКого, то легко показать, что среди построенных колебательных режимов найдется периодический режим.