Существующие здания с подпорными конструкциями

Территория города Большого Сочи, Российской Федерации характеризуется сложным рельефом с резким перепадом высот при весьма плотной застройке. Ситуации, при которых освоение нового участка осуществляется вблизи существующего здания с подрезкой грунта и устройством противооползневых мероприятий встречаются в этом регионе повсеместно. Ввиду отсутствия информации о конструктивных решениях уже построенного дома достаточно сложно оценить негативное влияние, оказываемое строительством подпорной стены на конструкции существующего здания [1]. Нередко расстояние между подпорной стеной и зданием не превышает и 3-х метров, что может привести к возникновению опасных оползневых процессов [2], [3], повреждению существующего здания [4]-[6], а также значительному материальному ущербу [7][9].

В связи с отсутствием в настоящее время единой методики оценки запредельных усилий, возникающих в существующем здании, актуальным остается вопрос влияния строительства подпорной стены в зоне с высокой плотностью застройки [10], [11]. Согласно рекомендациям действующих норм для существующего здания ограничивается лишь предельное значение дополнительной осадки основания фундаментов [12]. Изученная оценка влияния на существующую застройку, [13]-[15] во многом направлена на определение дополнительных осадок. Однако, в конструкциях здания, находящихся в зоне влияния нового строительства, возникают дополнительные усилия, на которые оно не было изначально рассчитано, что подтверждается исследованиями [16]-[18]. В связи с этим возникает необходимость разработки Saryan L.

The existing buildings with retaining structures;

методики оценки влияния нового строительства [19] и дать рекомендации по принятию оптимальных проектных решений, способствующих минимизации негативного влияния вновь возводимых сооружений на существующее здание [20]-[22].

Цель исследования – оценить влияние, оказываемое подрезкой грунта и строительством подпорной стены, расположенной вблизи существующего здания.

Задачи исследования:

• 1.    На основании результатов расчета изучить влияние, оказываемое подпорной стеной на напряженно-деформированное состояние конструкций существующего здания, в зависимости от высоты подпора грунта и расстоянию между зданием и удерживающим сооружением.

• 2.    Обосновать необходимость дальнейшего исследования в области несущей способности и устойчивости здания, находящегося в зоне влияния вновь возводимых противооползневых сооружений.

При устройстве противооползневых мероприятий вблизи существующей застройки помимо увеличения осадки фундамента [23]-[25], необходимо учитывать запредельные усилия, возникающие в конструкциях существующего здания [26]. Для оценки количественного влияния были произведены расчеты различных вариантов подпорной стены. Численный расчет производился на основании изученных методик [27], [28] в программном комплексе Plaxis 3D . Модель грунта была выбрана в соответствии с результатами расчета различных моделей [29], а также рекомендаций [30], учитывающих реализованные модели грунта в программном комплексе Plaxis 3D. Работа была поделена на три этапа. На каждом этапе были определены дополнительные осадки, возникающие в существующем здании, а также произведена оценка изменений усилий, возникающих в конструкциях существующего здания.

• 2    Materials and Methods

Расчет производился в программном комплексе Plaxis 3D, предназначенном для трехмерных расчетов деформации и устойчивости пространственных строительных объектов совместно с грунтовым основанием. Для наглядности полученных результатов в программном комплексе решалась осесимметричная задача.

Ход расчета был поделен на 3 основных этапа:

• 1.    Строительство здания. На данном этапе была определена максимальная осадка фундаментной плиты, а также усилия, возникающие в фундаментной плите, колоннах и балках по периметру.

• 2.    Устройство противооползневых мероприятий. На данном этапе была определена дополнительная осадка в фундаментной плите от устройства буронабивных свай, а также проанализированы изменения усилий, возникающих в фундаментной плите, колоннах и балках по периметру. Проведен сравнительный анализ с предыдущим этапом.

• 3.    Выемка котлована для нового строительства. На данном этапе была определена дополнительная осадка в фундаментной плите от выемки грунта котлована, а также проанализированы изменения усилий, возникающих в фундаментной плите, колоннах и балках по периметру. Проведен сравнительный анализ с предыдущим этапом.

Конструктивная схема здания представляет собой рамный каркас, опирающийся на фундаментную плиту по естественному основанию. Вертикальные нагрузки от перекрытий воспринимаются и передаются на основание системой из несущих ж/б ригелей, колонн. Шаг несущих элементов, опирающихся на фундаментную плиту в продольном и поперечном направлениях, составляет 5.0 м. Совместная работа плит перекрытий, ригелей, колонн обеспечивают пространственную жесткость здания. Класс бетона принят В25. Монолитная железобетонная фундаментная плита выполнена толщиной 500 мм. Колонны каркаса выполнены монолитные железобетонные сечением 400х400 мм. Плиты перекрытий выполнены толщиной 200 мм из монолитного железобетона. Балки каркаса (ригель по периметру) – монолитные железобетонные сечением 400х400 (h) с учетом толщины плиты перекрытия. Здание в плане представляет собой простую форму размерами 10х10 м.

Подпорная стена представляет собой буронабивные сваи, поверх которых выполняется монолитный ж/б ростверк. После выемки котлована по сваям устраивается облицовочная монолитная ж/б стена. Буронабивные сваи Ø820 мм (бетон В25) с жесткой заделкой свай в ростверк. Длина свай – 10.0 м.

Произвольный участок грунтового массива размерами 15х30 м. При задании параметров грунтов была выбрана модель линейно деформированного полупространства Мора-Кулона.

В качестве грунта использовались суглинок тяжелый твердый с отметкой низа подошвы -7.0 м, модулем деформации E=23Мпа, удельным сцеплением c=0.010МПа, углом внутреннего трения ȹ=8˚, а также глина легкая твердая с отметкой низа подошвы -20.0 м, модулем деформации E=11.8 МПа, удельным сцеплением c=0.030Мпа, углом внутреннего трения ȹ=19˚.

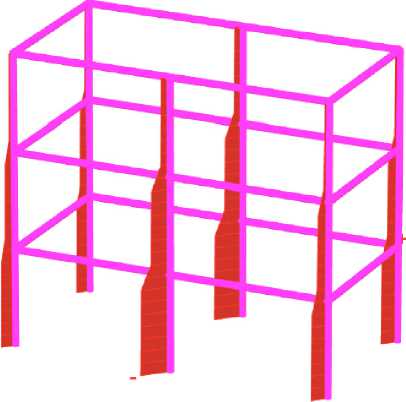
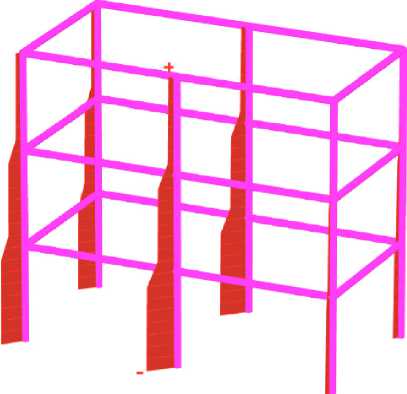
На рис. 1 представлена расчётная схема, выполненная в программном комплексе Plaxis 3D, высота подпора грунта принята 1.0 м, 3.0 м, 5.0 м. Расстояние от здания до подпорной стены – 1.0 м, 3.0 м, 6.0 м, 9.0 м.

[m]

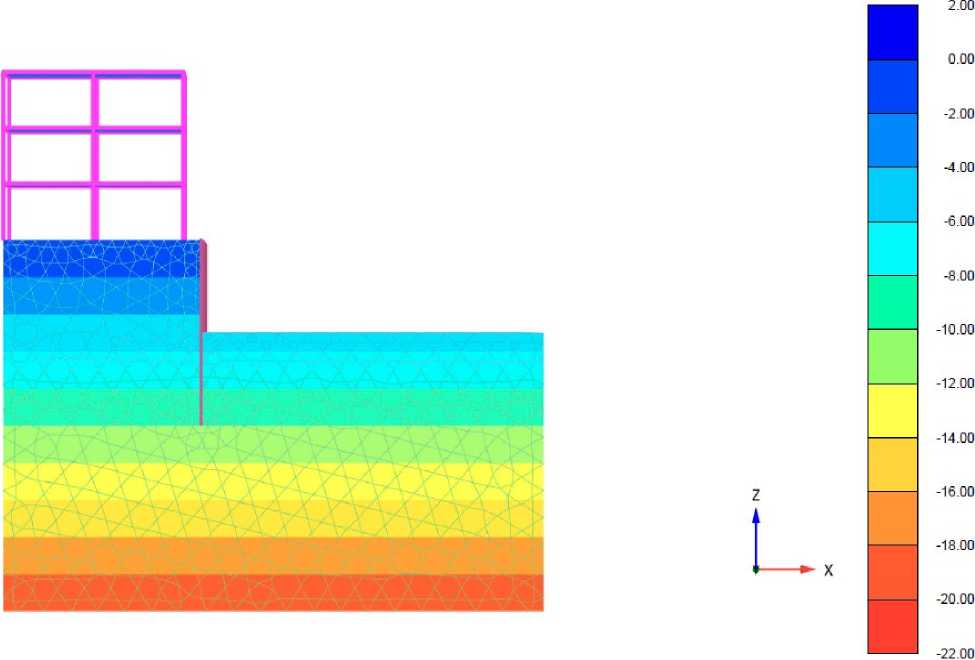
Рис. 1 – Расчетная схема

Fig. 1 – Design model

• 3    Results and Discussion

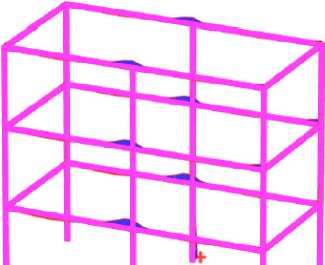
На первом этапе (строительство здания) эксперимента были определены перемещения фундаментной плиты от заданных нагрузок по оси Z. Вычислены усилия, возникающие в фундаментной плите, колоннах и балках.

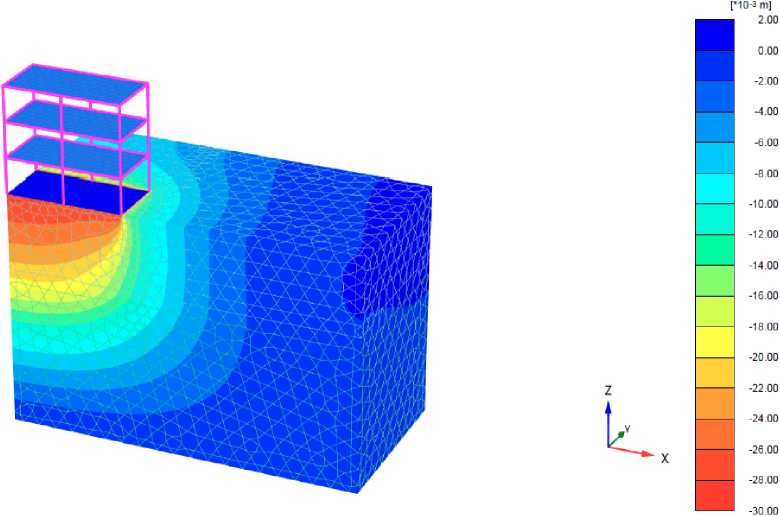
Total displacements uz (scaled up 50.0 times)

Maximum value = 0.2784*10-3 m (Element 1830 at Node 744)

Minimum value = -0.02886 m {Element 5626 at Node 7)

Рис. 2 – Максимальные перемещения расчетной модели (стадия строительство) по оси Z Fig. 2 – Total displacements of design model (construction phase) Z-direction

Максимальная осада фундаментной плиты составила u z =-0.02886 м. Ниже приведены изополя вычисленных нормальных усилий (N), сдвигающих усилий (Q) и изгибающих моментов (М).

[kN/m]

[kN/m]

Axial forces N2 (scaled up 0.0200 times)

Maximum value = 15 58 kN/m (Element 697 at Node 373)

Minimum value = -67.51 kN/m (Element 665 at Node 25)

20 00 I 15.00

I 10.00 J 5.00

J 0.00

_ -5.00

— -10.00

_ -15.00

_ -20 00 _ -25.00 _ -30.00

_ -35.00

_ -40.00 _ -45.00 _ -50.00 _ -55.00 _ -60.00 _ -65.00

Axial forces N1 {scaled up 0.0100 times)

Maximum value = 24.84 kN/m (Element 662 at Node 374)

Minimum value = -105.2 kN/m (Element 663 at Node 3B1)

30 00

_ 20 00

10.00

-10.00

-20 00

-30.00

-40.00

-50.00

-60.00

-7000

-80.00

-90.00

-100 00

-110 00

Рис. 3 – Нормальные усилия N 2 и N 1

Fig. 3 – Normal force N 2 and N 1

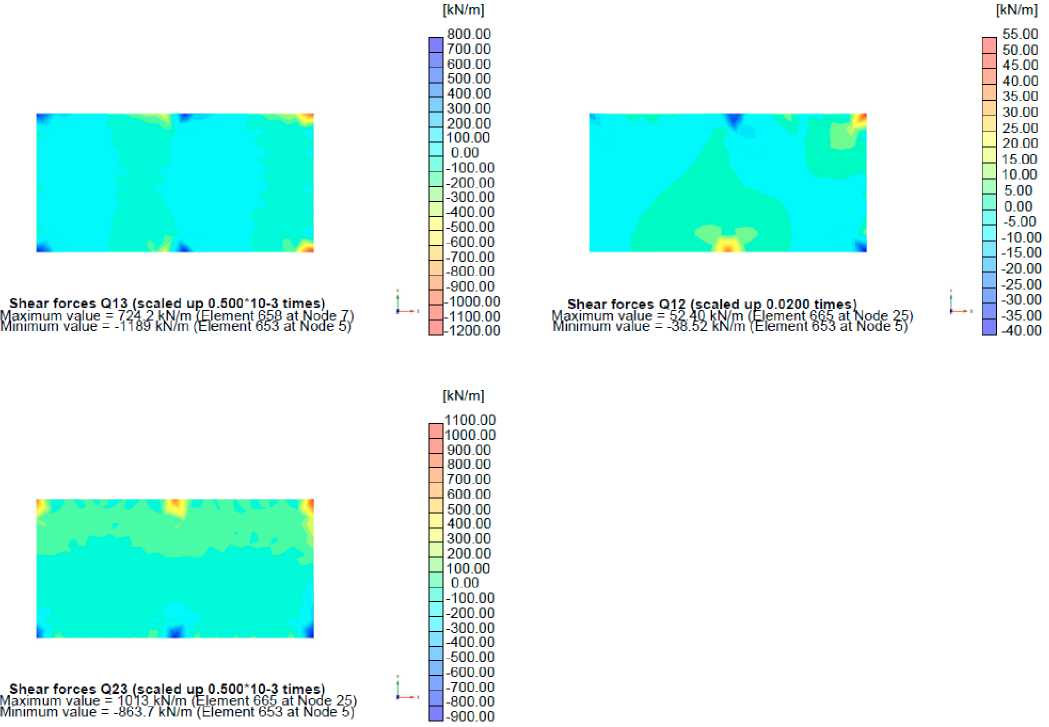
Рис. 4 – Сдвигающие усилия Q 12 , Q 23 , Q 13

Fig. 4 – Shear forces Q 12 , Q 23 , Q 13

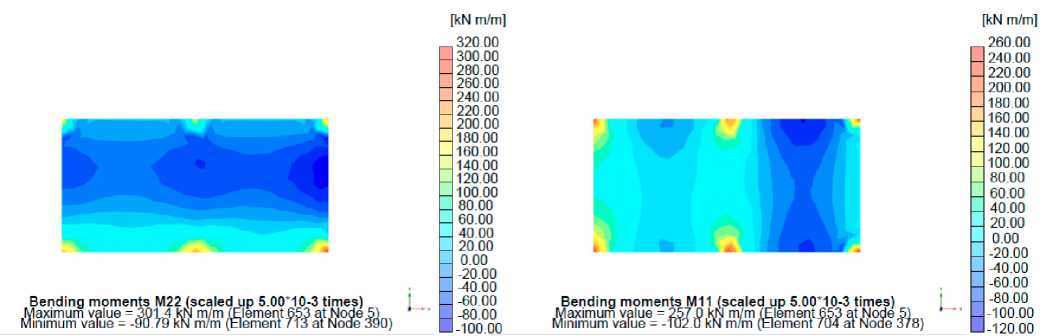
Рис. 5 – Изгибающий момент M 11 , M 22

Fig. 5 – Bending moment M 11 , M 22

Axial forces N (scaled up 2.00*10-3 times)

Maximum value = 29.04 kN (Element 174 at Node 37)

Minimum value = -446.6 kN (Element 179 at Node 6)

Bending moments M2 (scaled up 0.0100 times)

Maximum value = 84.73 kN m (Element 191 at Node 24)

Minimum value = -40.71 kN m (Element 125 at Node 1057)

Рис. 6 – Нормальные усилия N в колоннах, изгибающий момент M 2 в балках

Fig. 6 – Normal forces N in columns, bending moment M 2 in beams

Таблица 1. Усилия, возникающие в конструкциях здания на первой стадии расчета

Table 1. Forces occurring in the building structures at the first calculation stage

№	Наименование	N 1 , kN/m	N 2 , kN/m	Q 12 , kN/m	Q 23 , kN/m	Q 13 , kN/m	M 11 , kN*m	M 22 , kN*m	N, kN	M 2 , kN*m
1	Фундаментная плита	24.84	15.58	52.40	1013.0	724.2	257.0	301.4	-	-
		- 105.2	-67.51	-38.52	-863.7	-1189	- 102.0	-90.79
2	Колонны	-	-	-	-	-	-	-	29.04	-
									-446.6
3	Балки	-	-	-	-	-	-	-	-	84.73
										-40.71

Согласно результатам расчета на первой стадии эксперимента, максимальная осадка фундаментной плиты составила u z =-0.02886.

Максимальные нормальные усилия в фундаментной плите – N 1 =-205.2 kN/m, N 2 =-67.51kN/m. Максимальные сдвигающие усилия - Q 12 =52.4 kN/m, Q 23 =1013.0 kN/m, Q 13 =-1189.0 kN/m. Максимальные изгибающие моменты – M 11 =257.0 kN*m, M 22 =301.4 kN*m.

Максимальное усилие, действующее в колоннах – N=-446.6 kN. Центральные колонны самые нагруженные.

Максимальный изгибающий момент, возникающий в балках здания – M 2 =84.73 kN*m.

На втором этапе (устройство буронабивных свай) эксперимента были определены дополнительные перемещения фундаментной плиты по оси Z. Проанализированы изменения усилий, возникающие в фундаментной плите, колоннах и балках от устройство буронабивных свай на расстоянии 1 м от здания.

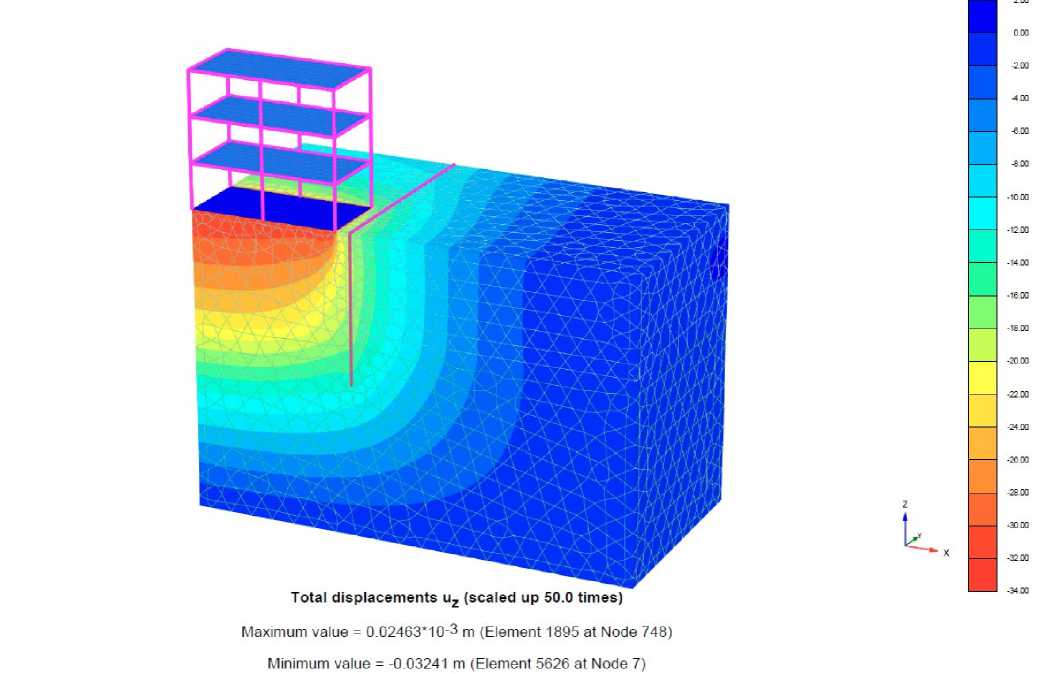
Рис. 7 – Максимальные перемещения расчетной модели (стадия устройство свай) по оси Z Fig.7 – Total displacements of the design model (pile installation phase) Z-direction

Дополнительное перемещение фундаментной плиты по оси Z от устройства буронабивных свай подпорной стены составило u z =-0.00355мм (+12.3%). На рисунках ниже представлены усилия в конструкциях здания, возникающие при устройстве противооползневых мероприятий.

[kN/m]

[kN/m]

Axial forces N2 (scaled up 0.0200 times)

Maximum value = 17.23 kN/m (Element 697 at Node 373)

Minimum value = -67.15 kN/m (Element 653 at Node 5)

20.00 ■ 15.00 ■ 10.00

_ 5.00

_ 0.00 _ -5.00

_ -10.00

_ -15.00 _ -20.00 _ -25.00 _ -30.00 _ -35.00 _ -40 00 _ 45.00 _ -50.00 _ -55.00 _ -60.00 _ -65.00

J -70.00

Axial forces N1 (scaled up 0.0100 times)

Maximum value = 25.28 kN/m (Element 666 at Node 388)

Minimum value = -94.15 kN/m (Element 653 at Node 5)

30.00

I 20.00

Ц 10.00 _ 0.00 _ -10.00 _ -20.00 _ -30.00 _ -40.00 _ -50.00 _ -60.00 _ -70.00 _ 80.00 _ -90 00

J-100.00

Рис. 8 – Нормальные усилия N 2 и N 1

Fig. 8 – Normal forces N 2 and N 1

Shear forces QI2 (scaled up 0.0100 times) Maximum value = 56.15 kN/m (Element 665 at Node 25) Minimum value = -48.26 kN/m (Element 653 at Node 5)

[kN/m]

60.00

50.00

40.00

30.00

20.00

10.00

0.00

-10.00

-20.00

-30.00

j__И-40.00

LI -50.00

[kN/m]

[kN/m]

Shear forces Q13 (scaled up 0.500*10-3 times)

Maximum value = 772.0 kN/m (Element 658 at Node 7)

Minimum value = -1145 kN/m (Element 653 at Node 5)

800.00 ■ 700.00 Ц 600.00 Ц 500.00 _ 400.00 _ 300.00 _ 200.00 _ 100.00 _ 0.00 _-100.00 _ -200.00 _ -300.00 _ -400.00 _ -500.00 _ -600.00 _-700.00 _ -800.00 _-900.00 --1000.00 --1100.00 1-1-1200.00

Рис. 9 – Сдвигающие усилия Q 12 , Q 23 , Q 13

Fig. 9 – Shear forces Q 12 , Q 23 , Q 13

[kN m/m]

280.00 260.00

240.00

220.00 200.00

180.00

160.00

140.00

120.00

100.00 80.00 60.00 40.00 20.00 0.00

-20.00

-40.00

-60.00

-80.00

Bending moments M11 (scaled up 5.00*10-3 times) *   1—1-100.00

Maximum value = 271.4 kN m/m (Element 653 at Node 5)       ■-120.00

Minimum value = -100.5 IkN m/m (Element 704 at Node 378)

Рис. 10 – Изгибающие моменты M 11 , M 22

Fig. 10 – Bending moments M 11 , M 22

Shear forces Q23 (scaled up 0.500’10-3 times)

Maximum value - 899.2 kN/m (Element 665 at Node 25)

Minimum value = -831.5 kN/m (Element 655 at Node 6)

Bending moments M22 (scaled up 5.00*10-3 times)

Maximum value = 278.4 kN m/m (Element 653 at Node 5)

Minimum value = -83.23 IkN m/m (Element 713 at Node 390)

.__.1000.00 _ 900.00 _ 800.00 _ 700.00 _ 600.00 _ 500.00 _ 400.00 _ 300.00 _ 200.00 _ 100.00 _ 0.00 _-100.00 _ -200.00 _ -300.00 _ -400.00 _ -500.00 L -600.00 Ц-700.00 Ц-800.00 ■-900.00

[kN m/m]

280.00

260.00

240.00

220.00

200.00

180.00

160.00

140.00

120.00

100.00

80.00

60.00

40.00

20.00

0.00

-20 00

-40.00

-60.00

-80.00

-100.00

Axial forces N (scaled up 2.00*10-3 times)

Maximum value = 26.87 kN (Element 174 at Node 37)

Minimum value = -457.7 kN (Element 179 at Node 6)

Bending moments M2 (scaled up 5.00*10-3 times)

Maximum value = 86.83 kN m (Element 191 at Node 24)

Minimum value = -53.44 kN m (Element 218 at Node 14)

Рис. 11 – Нормальные усилия N в колоннах, изгибающий момент M 2 в балках

Fig. 11 – Normal forces N in columns, bending moment M 2 in beams

Таблица 2. Усилия, возникающие в конструкциях здания на второй стадии расчета

Table 2. Forces occurring in the building structures at the second calculation stage

■ (+) ■ (-)

№	Наименование	N 1 , kN/m	N 2 , kN/m	Q 12 , kN/m	Q 23 , kN/m	Q 13 , kN/m	M 11 , kN*m	M 22 , kN*m	N, kN	M 2 , kN*m
1	Фундаментная плита	25.28	17.23	56.15	899.0	772.0	271.4	278.4	-	-
		-94.15	-67.15	-48.26	-831.5	-1145	-100.5	-83.23
2	Колонны	-	-	-	-	-	-	-	26.87	-
									457.7
3	Балки	-	-	-	-	-	-	-	-	86.83
										-53.44

30.00%

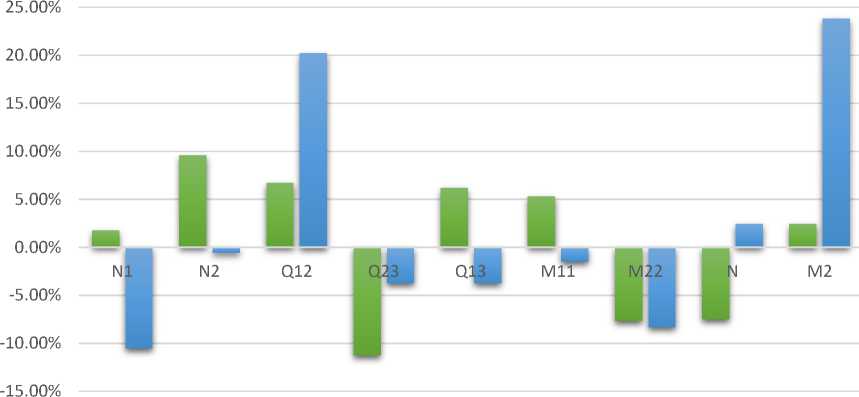
Рис. 12 – Изменение максимальных и минимальных значений усилий в конструкциях здания между первым и вторым этапом эксперимента

Fig. 12 – Changes in the maximum and minimum value of forces in building structures comparing the first and second stages of the experiment

Согласно результатам расчета второй стадии – устройство буронабивных свай, дополнительная осадка фундаментной плиты составила - u z =-0.00355мм (+12.3%), что не является критичным для данной конструкции и находится в рамках рекомендаций действующих норм. В связи с тем, что здание стремиться наклониться вперед происходит незначительное перераспределение усилий, максимальное изменение наблюдается в балках здания – момент в пролете увеличился на 24 %. Вследствие того, что изначальные усилия были не большими, приращение в 24% также не является критическим для такой конструкции, однако при реальном проектировании и приложении всех действующих нагрузок, а также сейсмических – приращение в 24 % может быть существенным. В рамках данного эксперимента нагрузки, действующие на здание, были сведены к минимумы, и поэтому необходимо учитывать прирост в процентном соотношении.

На третьем этапе (выемка грунта котлована) эксперимента были определены дополнительные перемещения фундаментной плиты по оси Z. Проанализированы изменения усилий, возникающие в фундаментной плите, колоннах и балках от выемки грунта котлована на высоту – 5 м.

[•10-э m|

ИСО

Total displacements uz (scaled up 10.0 times)

Maximum value = 0.07600 m (Element 5550 at Node 196)

Minimum value = 0.05698 m (Element 5103 at Node 5)

Рис. 13 – Максимальные перемещения расчетной модели (стадия выемки грунта) по оси Z

Fig. 13 – Total displacement of design model (excavation stage) Z-direction

Дополнительное перемещение фундаментной плиты по оси Z от устройства котлована высотой 5 м составило u z =-0.02457мм (+43.12%). На рисунках ниже представлены усилия в конструкциях здания, возникающие при устройстве противооползневых мероприятий.

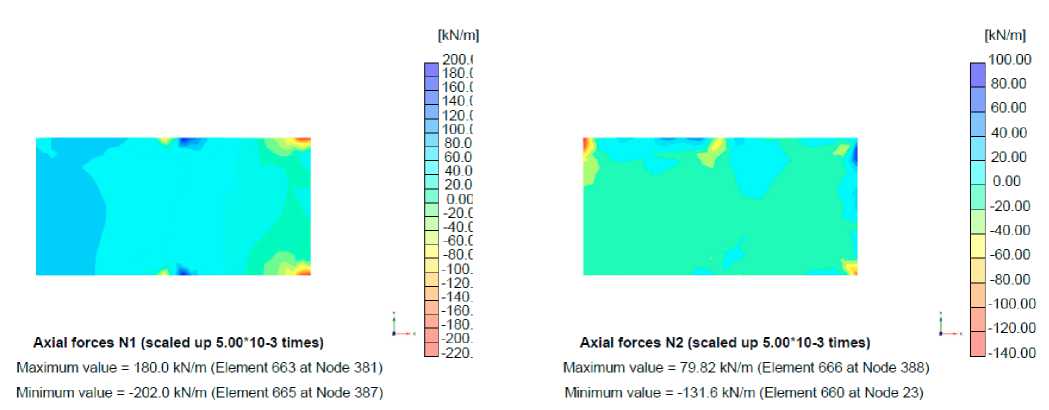
Рис. 14 – Нормальные усилия N 2 и N 1

Fig. 14 – Normal forces N 2 and N 1

[kN/m]

[kN/m]

Shear forces Q12 (scaled up 5.00*10-3 times)

Maximum value = 62.53 kN/m (Element 662 at Node 24)

Minimum value = -100.1 kN/m (Element 653 at Node 5)

70.00

60.00

50.00

40.00

30.00

20.00

10.00 0.00 -10.00

-20.00

-30.00

-40.00

-50.00

-60.00

-70.00

-80.00

-90.00

-100.00

-110.00

Shear forces Q13 (scaled up 0.500*10-3 times) Maximum value = 1326 kN/m (Element 658 at Node 7) Minimum value = -878.2 kN/m (Element 656 at Node 125)

1400.00

-1200.00

-1000.00

_ 800.00

_ 600.00

_ 400.00

_ 200.00

_ 0.00

_ -200.00

-400.00

-600.00

-800.00

-1000.00

[kN/m]

e1400.00

-1200.00

1000.00

800.00

400.00

200.00

0.00

-200.00

-400.00

-600.00

_-800.00 Ц-1000.00 1-1200.00 ■-1400.00

Shear forces Q23 (scaled up 0.500*10-3 times) Maximum value = 1367 kN/m (Element 660 at Node 23) Minimum value = -1327 kN/m (Element 658 at Node 7)

Рис. 15 – Сдвигающие усилия Q 12 , Q 23 , Q 13

Fig. 15 – Shear forces Q 12 , Q 23 , Q 13

[kN m/m]

[kN m/m]

„375.00 _ 350.00 _ 325.00 _ 300.00 _ 275.00 _ 250.00 _ 225.00 _ 200.00 -175.00 -150.00 -125.00 -100.00 _ 75 00 _ 50 00 _ 25 00 _ 0 00

Bending moments M11 (scaled up2.00‘10-3 times) ^

Maximum value = 351.4 kN m/m (Element 658 at Node 7)

Minimum value = -102.6 kN m/m (Element 691 at Node 364)

_ -25.00

_ -50.00

_ -75.00 _-100.00 U-125 00

Torsion moments M12 (scaled up 5.00*10-3 times)

Maximum value = 119 4 kN m/m (Element 653 at Node 5)

Minimum value = -130.2 kN m/m (Element 665 at Node 25)

120.00

100.00

80 00

60.00

40.00

20 00 0.00 -20 00 -40.00

-6000

-80.00

-100.00

-120.00

-14000

Рис. 16 – Изгибающие моменты M 11 , M 22

Fig. 1. – Bending moments M 11 , M 22

Axial farces N (scaled up 2.00*10-3 times)

Maximum value = 41.91 kN (Element 7 at Node 944)

Minimum value = -475.9 kN (Element 179 at Node 6)

Bending moments M2 (scaled up 5.00*10-3 times)

Maximum value = 144.0 kN m (Element 140 at Node 803)

Minimum value = -106.8 kN m (Element 146 at Node 38)

Рис. 17 – Нормальные усилия N в колоннах, изгибающий момент M 2 в балках

Fig. 17 – Normal forces N in columns, bending moment M 2 in beams

Таблица 3. Усилия, возникающие в конструкциях здания на третьей стадии расчета

Table 3. Forces occurring in building structures at the second calculation stage

№	Наименование	N 1 , kN/m	N 2 , kN/m	Q 12 , kN/m	Q 23 , kN/m	Q 13 , kN/m	M 11 , kN*m	M 22 , kN*m	N, kN	M 2 , kN*m
1	Фундаментная плита	180.0	79.82	62.53	1367.0	1326.0	351.4	386.0	-	-
		202.0	- 131.6	-100.1	-1327	-878.2	- 102.6	-99.55
2	Колонны	-	-	-	-	-	-	-	41.91	-
									-475.9
3	Балки	-	-	-	-	-	-	-	-	144.0
										- 106.8

-40.00%

■ (+) ■ (-)

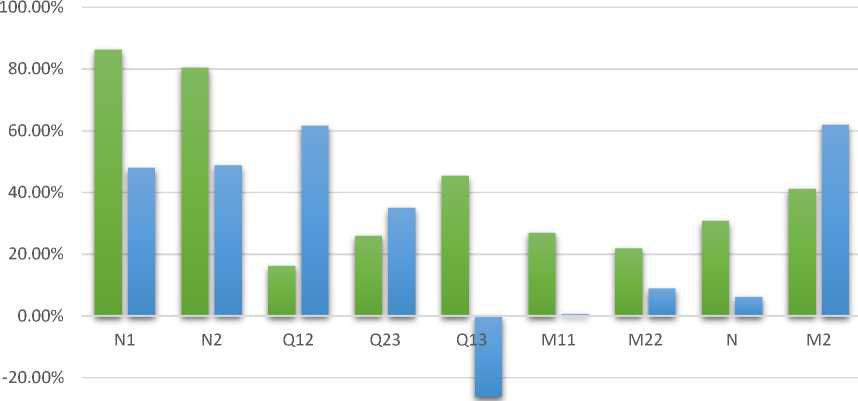
Рис. 18 – Изменение максимальных и минимальных значений усилий в конструкциях здания между первым и третьим этапом эксперимента

Fig. 18 – Changes in the maximum and minimum value of forces in building structures comparing the first and third stages of the experiment

Согласно результатам расчета третьего этапа – срез грунта, дополнительная осадка фундаментной плиты составила - u z =-0.02457мм (+43.12%). Перемещение оголовка свай по Х составило u x =0.06095 м.

Максимальное изменение усилий в конструкциях здания после среза грунта высотой 5 м составило +86.2 % - нормальное усилие N 1 , +80.48 % - нормальное усилие N 2 . Прирост сдвигающих усилий составил - +61.5 %, + 45.38 %, + 34.91% соответственно для Q 12 , Q 13 , Q 23 . Несущественным оказался прирост изгибающих моментов в фундаментной плите М 11 и M 22 .

В колоннах здания увеличение усилия составило +30.7 %. По результатам первой стадии расчета самые нагруженные были первые 2 ряда колонн, однако после выполнения третьего этапа имело место перераспределение усилий в колоннах. Так более нагруженные стали последние 2 ряда колонн, когда усилие в первом ряду колонн сократилось.

В балках, расположенных по периметру здания наблюдается увеличение момента в пролете на +62%, на опоре - +41%.

60.00%

50.00%

40.00%

30.00%

20.00%

10.00%

0.00%

Hк=5м Hк=5м Hк=5м Hк=5м Hк=3м Hк=3м Hк=3м Hк=3м Hк=1м Hк=1м Hк=1м Hк=1м

L=1м L=3м  L=6м  L=9м  L=1м L=3м  L=6м  L=9м L=1м L=3м  L=6м  L=9м

« ■ матн»Дополнительная осадка по оси Z

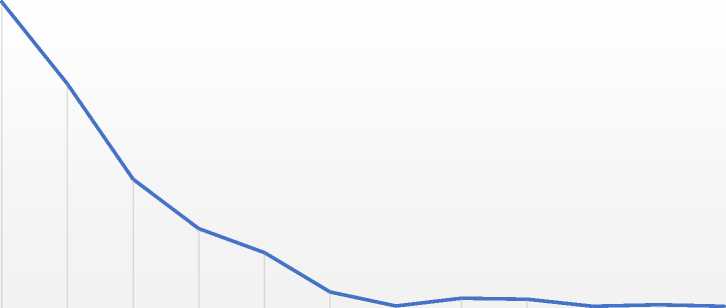
Рис. 19 – Изменение дополнительного перемещения фундаментной плиты по оси Z в зависимости от высоты подпора грунта (Hк) и расстоянию от здания до подпорной стеной (L) Fig. 19 – Changes in the additional displacement of the foundation slab Z – direction depending on the height of earth- retaining wall (Hк) and distance between the building itself and retaining wall (L)

Результаты расчета различных вариантов устройства подпорной стены показаны на рис. 19. Согласно представленному графику при высоте подпора грунта Н к менее 3-х метров и расстоянию между зданием и подпорной L стеной более 3-х метров дополнительная осадка фундамента здания составила менее 10 %, что не является критичным для данного типа конструкции.

60.00%

50.00%

40.00%

30.00%

20.00%

10.00%

0.00%

-10.00%

-20.00%

-30.00%

—•— |N1| —•— |N2| —•— |Q12| —•— |Q23| —•— |Q13|

—•— |M11| —•— |M22| —•— |N|  —•— |M2|

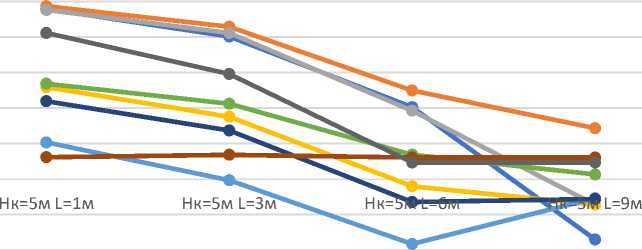
Рис. 20 – Изменение максимальных усилий в конструкциях здания при высоте подпора грунта Н к =5м и расстоянии между зданием и подпорной стеной L = 1м, L = 3м, L = 6м, L = 9м Fig. 20 – Changes in the maximum force values in building structures at the height of earthretaining wall Н к =5м and distance between the building and retaining wall L = 1м, L = 3м, L = 6м, L = 9м

25.00%

20.00%

15.00%

10.00%

5.00%

0.00%

-5.00%

-10.00%

-15.00%

-20.00%

=3м L=9м

—•— |N1| —•— |N2| —•— |Q12| —•— |Q23| —•— |Q13|

—•— |M11| —•— |M22| —•— |N|  —•— |M2|

Hк=3м L=1м

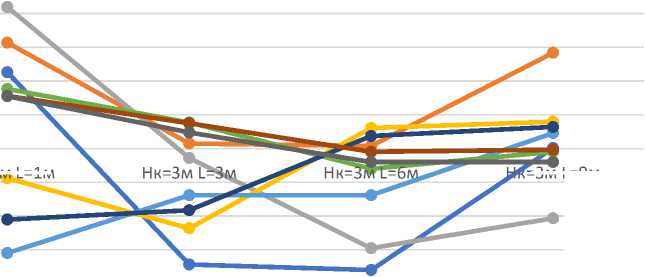
Рис. 21 – Изменение максимальных усилий в конструкциях здания при высоте подпора грунта Н к =3м, расстоянию между зданием и подпорной стеной L = 1м, L = 3м, L = 6м, L = 9м Fig. 21 – Changes in the maximum force values in building structures at the height of earthretaining wall Н к =3м and distance between the building and retaining wall L = 1м, L = 3м, L = 6м, L = 9м

30.00%

25.00%

20.00%

15.00%

10.00%

5.00%

0.00%

-5.00%

-10.00%

-15.00%

Hк=1м L=1м

Hк=1м L=6м

Hк=1м L=9м

-20.00%

—•— |N1| —•— |N2| —•— |Q12| —•— |Q23| —•— |Q13|

—•— |M11| —•— |M22| —•— |N|  —•— |M2|

Рис. 22 – Изменение максимальных усилий в конструкциях здания при высоте подпора грунта Н к =1м, расстоянию между зданием и подпорной стеной L = 1м, L = 3м, L = 6м, L = 9м Fig. 22 – Changes in the maximum force values in building structures at the height of earthretaining wall Н к =1м and distance between the building and retaining wall L = 1м, L = 3м, L = 6м, L = 9м

• 4    Conclusions

• 1.    Строительство подпорной стены вблизи существующего здания приводит к значительному увеличению осадки фундаментной плиты, а также увеличению максимальных усилий, действующих в конструкциях здания. В отдельных случаях увеличение усилий составило более 80%. Учитывая тот факт, что изначально здание не было рассчитано на такие нагрузки, строительство подпорной стены и устройство откоса без учета влияния на существующую застройку может привести к значительному материальному и другим видам ущерба.

• 2.    Влияние, оказываемое подпорной стеной, в большей степени зависит от инженерногеологических условий площадки строительства, высоты подпора грунта и расстоянию между удерживающим сооружением и существующим зданием.

• 3.    На основании результатов эксперимента было выявлено, что при высоте подпорной стены H k <3м и при расстоянии L>3м прирост усилий в конструкциях здания не превышает 10 %, что не является критическим для данного типа сооружений. При большей высоте подпора грунта и меньшему расстоянию до здания необходимо учитывать дополнительные усилия, возникающие в конструкциях существующей застройки.