СВЧ фотонные кристаллы - новый тип функциональных структур, применяемых в радиоэлектронике

Известны примеры создания фотонных кристаллов в оптическом, инфракрасном, ультрафиолетовом, СВЧ-диапазоне. В сверхвысокочастотном диапазоне фотонный кристалл может быть реализован как с помощью волноводов с диэлектрическим заполнением [1; 2], так и с использованием плоских линий передачи с периодически изменяющейся структурой полоска [3]. Для СВЧ-диапазона создать фотонный кристалл наиболее просто. Отметим, что при теоретическом описании свойств таких структур, в отличие, например, от сверхрешеток, нет необходимости учитывать свойства переходных слоев, квантовомеханические размерные эффекты, специфику технологических процессов. Это открывает возможность более точно рассматривать свойства фотонных кристаллов, связанные с периодичностью и, в частности, использовать результаты теоретического описания для измерения параметров входящих в кристалл слоев в результате решения соответствующей обратной задачи.

Возможности практического применения СВЧ фотонных кристаллов в качестве функциональных структур, применяемых в радиоэлектронике, рассматривались в [4–8]. В качестве примеров приводятся высоконаправленные резонансные антенны, резонансные полости для размещения полупроводниковых детекторов, различные типы СВЧ-фильтров, в том числе с управляемыми характеристиками.

В настоящей работе рассмотрены возможности новых практических применений свойств СВЧ фотонных кристаллов в качестве функциональных структур радиоэлектроники.

Периодические структуры на основе резонаторов в качестве замедляющих систем для вакуумных СВЧ-приборов и СВЧ-фильтров были описаны еще в 60-е года прошлого века [9; 10]. Они предназначались для использования в качестве замедляющих систем в этих приборах, обеспечивающих оптимальное взаимодействие электронного потока с электромагнитной волной.

Исследуемая авторами [11] структура состоит из периодически расположенных металлических резонансных диафрагм на расстоянии l друг от друга, нанесенных на диэлектрическую подложку (рис. 1).

На основе численного моделирования с использованием метода конечных элементов в программе ANSYS HFSS исследовалось влияние подложек с различной диэлектрической проницаемостью на коэффициенты отражения и прохождения СВЧ-волны для структуры.

Из полученных результатов следует, что амплитудно-частотная характеристика коэффициента пропускания исследуемой структуры имеет «зонный» характер. Амплитудно-частотные ха-

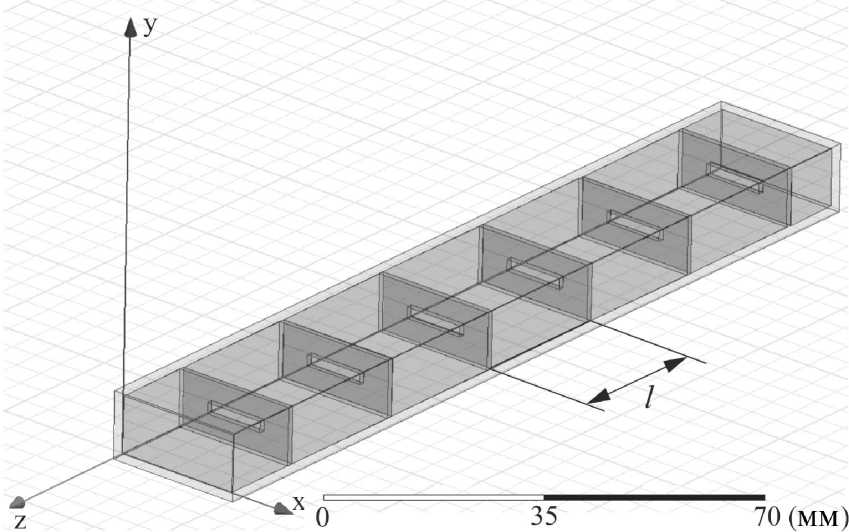
Рис. 1. Схема СВЧ фотонного кристалла, где l — расстояние между диафрагмами

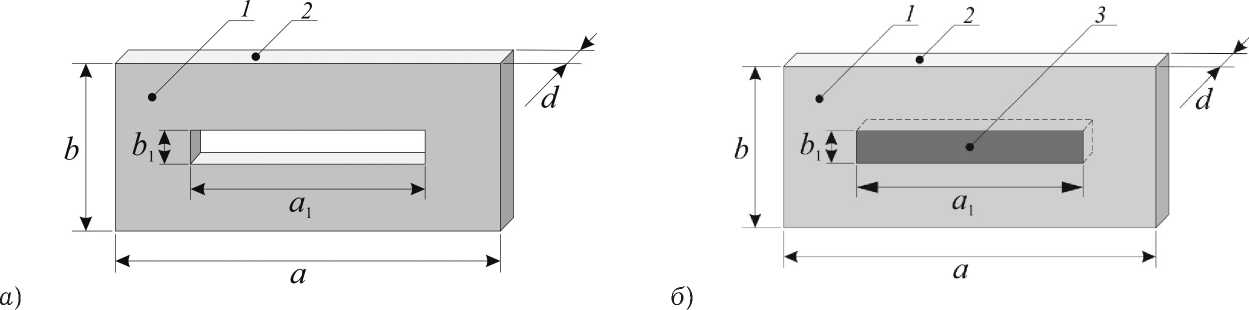
Рис. 2. Металлическая диафрагма 1 на подложке 2 из диэлектрика с E i: а ) со сквозной щелью; б ) со щелью заполненной диэлектриком 3 с диэлектрической проницаемостью ε ₂

рактеристики (АЧХ) такого фотонного кристалла состоит из характерных чередующихся «разрешенных» и «запрещенных» зон. Причем, резонансы отдельных диафрагм могут находиться за пределами исследуемой частотной области, так как резонансные пики пропускания в фотонном кристалле образуются за счет формирования стоячих волн в промежутках между диафрагмами, а изменение параметров диафрагм (ширина и высота щели) позволяют сдвигать «разрешенную» и «запрещенную» зоны в нужный частотный диапазон.

Проанализированы АЧХ фотонного кристалла, составленного из металлических диафрагм, нанесенных на диэлектрическую подложку со сквозной щелью (рис. 2, а ), при различной ширине щели a и АЧХ фотонного кристалла из диафрагм на диэлектрических подложках со щелями, заполненными материалом с диэлектрической проницаемостью ε ₂ (рис. 2, б ).

Можно заметить, что с увеличением ширины щели a, при фиксированной диэлектрической проницаемости подложки (рис. 2, а), увеличивается ширина и глубина запрещенной зоны. При- чем, низкочастотный край зоны остается неподвижным в районе 9 ГГц, а расширение происходит за счет смещения высокочастотного края запрещенной зоны в высокочастотную область. Такая же тенденция наблюдается, при увеличении диэлектрической проницаемости диэлектрика внутри щели (рис. 2, б).

В результате численного моделирования были получены частотные зависимости коэффициентов прохождения D , приведенные на рис. 3.

Схожесть поведения амплитудно-частотных характеристик фотонного кристалла при изменении диэлектрика внутри щели и при изменении ширины щели связана с тем, что с увеличением диэлектрической проницаемости материала внутри щели на фиксированной частоте уменьшается длина волны в нем, что эквивалентно увеличению линейных размеров щели.

Было исследовано влияние изменения диэлектрической проницаемости подложки ε ₁ для фотонного кристалла из диафрагм со сквозной щелью (рис. 2, а ). На рис. 4 представлены АЧХ фотонного кристалла, составленного из диафрагм на диэлектрике со сквозной щелью, при

\D\2, дБ

\D\2, дБ

-20

-20

-40

-40 L

-60

-60

-80

/ГГц

-80 L

б )

/ГГц

Рис. 3. Частотные зависимости | D |² для фотонного кристалла из диафрагм на подложках с £ 1 = 4.15, высотой щели Ь 1 = 2 мм, толщиной диэлектрика d = 1 мм: а ) со сквозной щелью различной ширины a _b мм: 1 — 10; 2 — 11; 3 — 12; 4 — 13; 5 — 14; б ) с щелью шириной а 1 = 10 мм, заполненной диэлектриком с различной величиной диэлектрической проницаемости £ 2 : 1 — £ 2 = 1; 2 — £ 2 = 2; 3 — £ 2 = 3; 4 — £ 2 = 4; 5 — £ 2 = 5

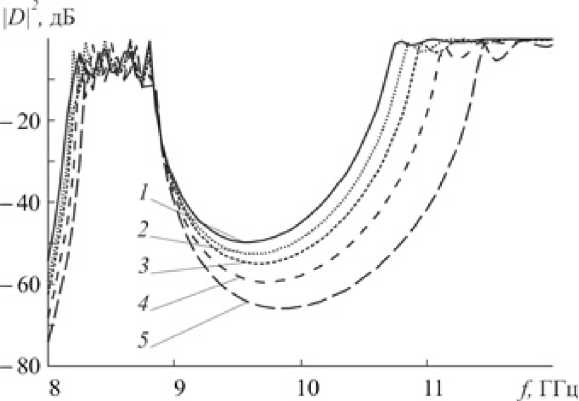
Рис. 4. Частотные зависимости коэффициента прохождения для фотонного кристалла из диафрагм на подложках со сквозной щелью, шириной щели а 1 = 10 мм, высотой щели Ь 1 = 2 мм, толщиной диэлектрика d = 1 мм: 1 — при £ 1 = 1; 2 — £ 1 = 3; 3 — £ 1 = 5; 4 — £ 1 = 7; 5 — £ 1 = 9

различных значениях диэлектрической проницаемости подложки.

Из результатов, представленных на рис. 4, следует, что изменение диэлектрической проницаемости подложек со сквозными щелями не в такой степени изменяет АЧХ фотонного кристалла, как в случае, когда диэлектрическая подложка заполняла щель диафрагмы. Это можно объяснить тем, что толщина подложки, равная 1 мм, мала по сравнению с расстоянием между диафрагмами, равным 25 мм.

Экспериментально исследовались фотонные кристаллы, созданные из периодически расположенных металлических резонансных диафрагм на расстоянии l друг от друга, нанесенных на диэлектрические подложки и без подложек.

Измерение частотных зависимостей коэффициентов пропускания и отражения исследуемых фотонных кристаллов проводились с помощью

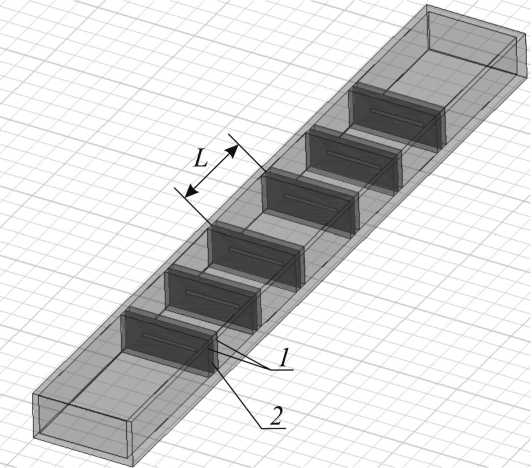
Рис. 5. Схема фотонного кристалла на основе диафрагм без диэлектрических подложек, где: 1 – пенопласт, 2 – металлическая диафрагма, L – размер нарушения в центральном слое векторного анализатора цепей Agilent PNA-L Network Analyzer N5230A в диапазоне частот 8–12 ГГц.

Фотонный кристалл на основе диафрагм без диэлектрических подложек состоял из шести алюминиевых диафрагм толщиной 10 мкм, зафиксированных между двумя слоями пенопласта толщиной 2 мм, размещенных в прямоугольном волноводе (см. рис. 5).

Ширина и высота щелей диафрагм фотонного кристалла выбирались равными 14 мм и 1 мм, соответственно, это обеспечивало возникновение в диапазоне частот 8–12 ГГц одной разрешенной и одной запрещенной зон на частотных зависимостях коэффициентов прохождения D ₂ и отражения R ₂ (штриховые кривые на рис. 6, а и рис. 6, б , соответственно). На этих же рисунках

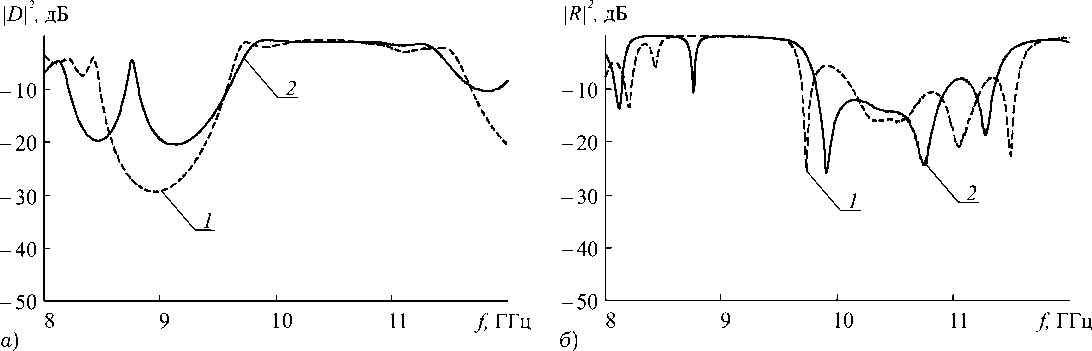
Рис. 6. Экспериментальные амплитудно-частотные характеристики коэффициента прохождения ( а ) и отражения ( б ) фотонного кристалла на основе диафрагм без диэлектрических подложек без нарушения (кривая 1 ) и с нарушением периодичности (кривая 2 ). Расстояние между диафрагмами l = 27 мм, длина щелей a ₁ = 14 мм, размер нарушения в центральном слое L = 20 мм

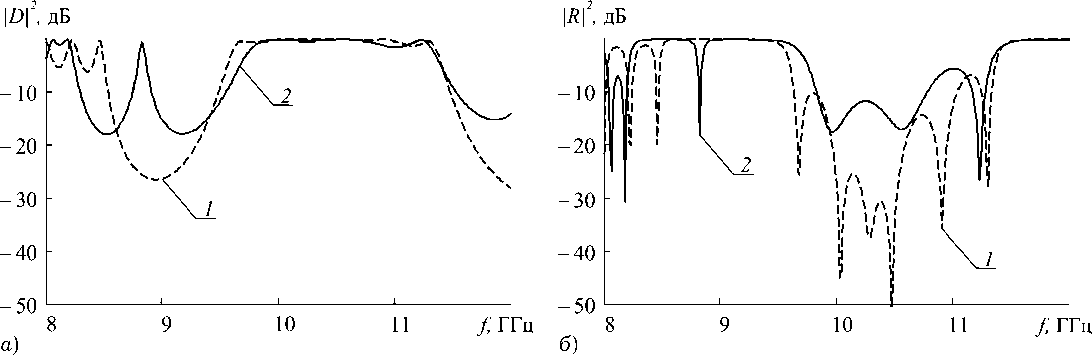
Рис. 7. Расчетные амплитудно-частотные характеристики коэффициента прохождения ( а ) и отражения ( б ) фотонного кристалла на основе диафрагм без диэлектрических подложек без нарушения (кривая 1 ) и с нарушением периодичности (кривая 2 ). Расстояние между диафрагмами 27 мм, длина щелей 14 мм, размер нарушения в центральном слое 20 мм

представлены результаты измерений АЧХ фотонного кристалла с нарушением периодичности (сплошные кривые) в виде измененного расстояния L между центральными диафрагмами.

Результаты расчета АЧХ фотонного кристалла на основе диафрагм без диэлектрических подложек с нарушением и без нарушения периодичности с параметрами, соответствующими описанному выше экспериментальному образцу, приведены на рис. 7, а ,б .

Сравнение экспериментальных зависимостей, представленных на рис. 6, с результатами расчета, приведенными на рис. 7, свидетельствует о хорошем качественном и количественном соответствии. При этом, как это следует из эксперимента и результатов расчета, создание нарушения в фотонном кристалле в виде уменьшенного расстояния между центральными диафрагмами приводит к возникновению пика пропускания в запрещенной зоне и увеличению ее ширины.

Экспериментально исследовались фотонные кристаллы, созданные из периодически распо- ложенных на фиксированном расстоянии друг от друга металлических резонансных диафрагм, нанесенных на сплошные диэлектрические подложки и диэлектрические подложки со сквозными щелями. Экспериментальные АЧХ фотонного кристалла, созданного из периодически расположенных на фиксированном расстоянии друг от друга металлических резонансных диафрагм, нанесенных на сплошные диэлектрические подложки, представлены на рис. 8, а. Результаты расчета АЧХ фотонного кристалла на основе периодически расположенных диафрагм со сплошными диэлектрическими подложками с параметрами, соответствующими описанному выше экспериментальному образцу, приведены на рис. 8, б.

Результаты, представленные на рис. 8, а и 8, б , свидетельствуют об их хорошем качественном и количественном соответствии, при этом в частотной области, соответствующей разрешенной зоне, наблюдаются ярко выраженные пики пропускания, количество которых на единицу

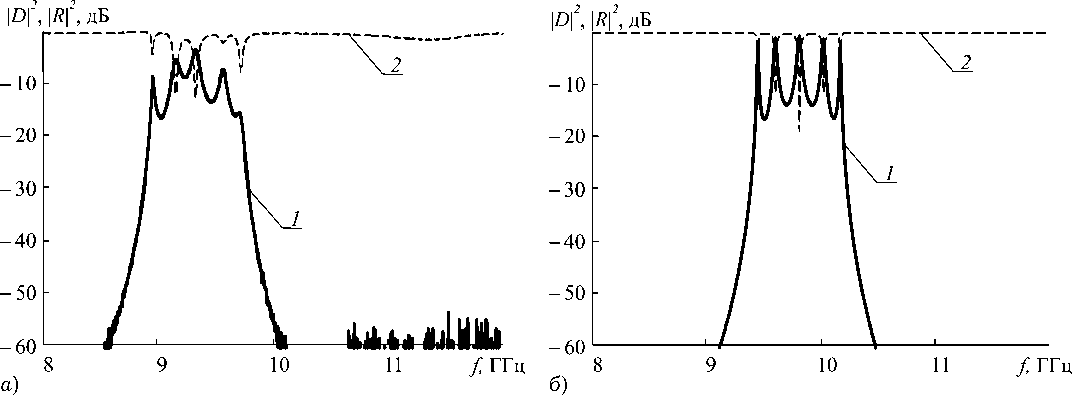
Рис. 8. АЧХ фотонного кристалла на основе периодически расположенных диафрагм со сплошными диэлектрическими подложками коэффициентов отражения (кривая 2 ) и прохождения (кривая 1 ). Расстояние между пластинами l = 25 мм, ширина щели a ₁ = 14 мм, высота щели b ₁ = 2 мм: а ) эксперимент; б ) расчет

меньше числа диафрагм, образующих фотонный кристалл.

Известны широко применяемые в технике СВЧ-устройства, называемые СВЧ-нагрузками. Проблема конструирования широкополосных согласованных нагрузок, несмотря на продолжительную историю их существования, и сегодня остается одной из актуальных задач СВЧ-радиоэлектроники. СВЧ-нагрузки широко применяются как самостоятельно, так и в составе сложных функциональных устройств: направленных ответвителей, сумматоров, измерителей мощности, измерительных мостов, фильтров и т. д. [12; 13]. Одной из основных задач, которую необходимо решить при создании согласованных нагрузок, предназначенных для работы на малых и средних уровнях мощности СВЧ-излучения, является обеспечение согласования в максимально широком диапазоне частот при минимальных габаритах конструкции. Для решения такой задачи, как показано в [14], можно использовать свойства СВЧ-фотонных кристаллов. В [15; 16] для обеспечения согласования было предложено использовать частотные зависимости коэффициента отражения электромагнитного излучения СВЧ диапазона от фотонных кристаллов, содержащих нанометровые металлические слои.

Актуальной остается задача расширения диапазона рабочих частот малогабаритных согласованных нагрузок на основе фотонных кристаллов до диапазонов, соответствующих стандартным сечениям волноводов в возможно большем числе используемых на практике СВЧ-диапазонов.

Однако, как показывают расчеты, для получения таких результатов с использованием СВЧ

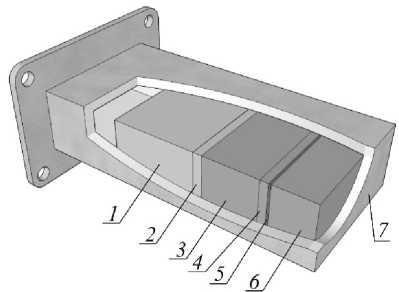
Рис. 9. Конструкция согласованной нагрузки, включающей слои композитного материала 1 и 3 , сплошные диэлектрические слои 2 , 4 и 6 и нанометровую металлическую пленку 5

фотонных кристаллов необходимо создавать не только нанометровые металлические слои с определенным значением поверхностного сопротивления, но и использовать диэлектрические слои, обладающие строго определенными значениями диэлектрической проницаемости и толщины. Такая возможность открывается, если использовать для создания диэлектрических слоев широко применяемые на СВЧ диэлектрические материалы, такие как тефлон и поликор (керамика Al2O3), в которых путем создания воздушных включений обеспечивается получение требуемых значений эффективной диэлектрической проницаемости с высокой степенью точности [17].

Слои исследуемых фотонных кристаллов, содержащие большое число воздушных включений, можно рассматривать как композитные материалы, представляющие собой диэлектрические матрицы на основе керамики с наполнителем в виде воздушных включений. Известно, что диэлектрические свойства композитных материалов могут быть охарактеризованы величи-

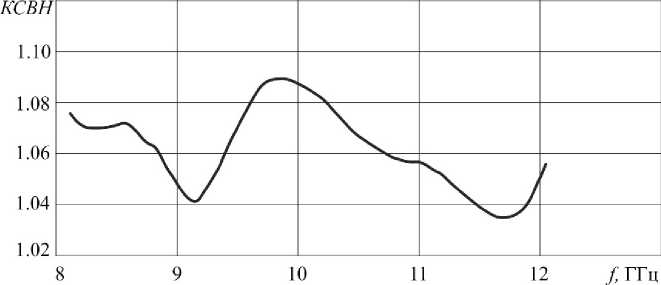
Рис. 10. Экспериментальная частотная зависимость КСВН в диапазоне 8.15-12.05 ГГц

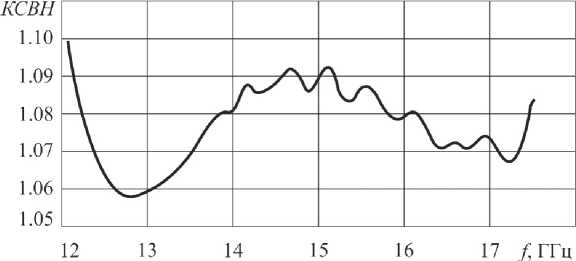
Рис. 11. Экспериментальная частотная зависимость КСВН в диапазоне 12.05-17.44 ГГц

ной эффективной диэлектрической проницаемости s ef , определяемой величинами диэлектрических проницаемостей матрицы S 1 , наполнителя S 2 и их объемными долями.

Величина эффективной диэлектрической проницаемости композитного материала, созданного на основе диэлектрической матрицы с наполнителем в виде воздушных включений, может быть также рассчитана и с использованием модели «эффективной» среды, описываемой, например, соотношением Бруггемана [18]

s — s         So — s x1—--— + x 2—--— = 0.             (1)

• ^{2 s} ef ^{+ S} 1       ^{2 s} ef ^{+ s} 2

Конструкция согласованных нагрузок, выполненных в виде многослойных металлодиэлектрических структур, состоящих из чередующихся слоев композитного материала, созданного на основе диэлектрической матрицы с наполнителем в виде воздушных включений, характеризующегося эффективной диэлектрической проницаемостью, и нанометровой металлической пленки, нанесенной на керамическую подложку (Al2O3), представлена на рис. 9.

По данным численного эксперимента были изготовлены широкополосные волноводные согласованные нагрузки на основе СВЧ фотонных кристаллов [19; 20].

Измерения частотных зависимостей коэффициентов стоячей волны по напряжению (рис. 10 —

• 13) созданных согласованных нагрузок и предназначенных для использования в диапазонах частот 8.15–12.05 ГГц, 12.05–17.44 ГГц, 17.44– 25.95 ГГц и 25.95–37.50 ГГц проводились с помощью векторного анализатора цепей Agilent PNA N5230A.

Как следует из результатов эксперимента, созданные на основе СВЧ фотонных кристаллов согласованные нагрузки, предназначенные для использования в диапазонах 8.15–12.05 ГГц, 12.05– 17.44 ГГц, 17.44–25.95 ГГц имеют КСВН < 1.10 при линейных размерах нагрузок менее 15 мм, 10 мм и 9 мм, соответственно. Согласованные нагрузки для диапазонов частот 25.95–37.50 ГГц, 37.50–53.57 ГГц имеют величину КСВН менее 1.15 при линейных размерах, не превышающих 7 мм и 6 мм.

Таким образом, в работе рассмотрены возможности новых практических применений свойств СВЧ фотонных кристаллов в качестве функциональных структур радиоэлектроники, среди которых СВЧ-фильтры на основе системы резонансных диафрагм, малогабаритные широкополосные согласованные нагрузки в сантиметровом и миллиметровом диапазонах на основе СВЧ фотонных кристаллов, состоящих из чередующихся нанометровых металлических слоев с различными значениями толщины и электропроводности и слоев композитных материалов,

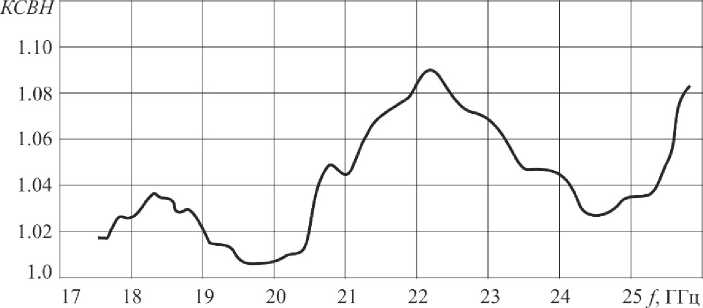
Рис. 12. Экспериментальная частотная зависимость КСВН в диапазоне 17.44-25.95 ГГц

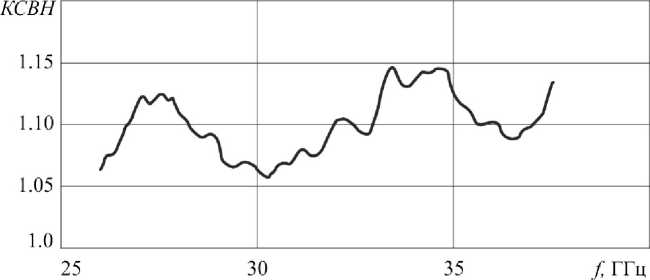
Рис. 13. Экспериментальная частотная зависимость КСВН в диапазоне 25.95-37.50 ГГц

представляющих собой диэлектрические матрицы с наполнителем в виде воздушных включений.

Работа выполнена при финансовой поддержке Министерства образования и науки РФ (государственное задание № 1376 и 1575).