Связь государственной и частной собственности в системе экономического роста и политических режимов

Какой должна быть экономическая модель государства с соответствующим политическим режимом, обеспечивающая высокую вероятность наивысшего экономического роста? Попытка ответить на этот вопрос и представлена в статье, где также критикуются выводы, сделанные Ф. Энгельсом в его монографии «Происхождение семьи, частной собственности и государства» [1], относительно ликвидации государства.

Очевидно, распределение собственности является ключевым фактором экономической деятельности народов, их процветания или упадка. Это распределение собственности всегда тесно свя- 78 зано с политическим режимом, то есть уровнем свободы, существующим в данном обществе, и перспективами развития этого общества, включая экономический рост. Экономическая свобода может рассматриваться как выпуск товаров и услуг, поскольку от их количества зависит возможность выбора продавцов и покупателей на товарных рынках.

Положим, что существует два крайних способа распределения собственности. Назовем первый способ распределения чистым капитализмом, когда вся собственность является частной, а второй – чистым коммунизмом, когда вся собственность является общественной (коллективной) или государственной. Между этими двумя крайними способами существует бесконечное множество комбинаций распределений собственности, обеспечивающее соответствующую агрегированную производственную функцию, или функцию выпуска товаров и услуг. Допустим при этом, что социализм – это когда больше половины всей собственности в государстве является государственной или общественной, а капитализм большего или меньше- го масштаба – когда больше половины всей собственности в стране является частной.

Ниже будет показано поведение двух моделей нетипичных производственных функций, зависящих от распределения собственности в моделируемом среднестатистическом государстве при прочих равных условиях. Эти модели являются демонстрационными, а не объясняющими. То есть они будут показывать величину выпуска продукции – товаров и услуг на данной территории в зависимости от комбинации количеств частной и коллективной собственности. Вид производственной функции будет нетипичным и, в частности, отличным от того, который 78 мы видим в модели экономического роста Роберта Солоу, где выпуск товаров и услуг зависит от факторов производства – труда и капитала (более сложные вариации с включением в модель народонаселения, качества образования, технологического прогресса и т.д. в статье не рассматриваются).

В нижеследующих моделях зависимая переменная остается той же, что и в упрощенной модели Роберта Солоу – количеством товаров и услуг, например, выраженном в денежном эквиваленте, а независимыми переменными выступают не труд и капитал, а доли или количество частной и государственной собственности, используемые в производстве товаров и услуг.

По существу, это означает, что производственная функция в виде выпуска товаров и услуг зависит от соотношения двух переменных – государственной и частной собственности, образуя в трехмерном пространстве x0yz-поверхность, которую мы не будем исследовать непосредственно, а упростим задачу, сведя ее к плоскости, решая в общем виде соот- ветствующие дифференциальные уравнения.

Государственная и частная собственность в данном случае выступают в виде ресурсов совершенных заместителей, что на плоскости x0y даст прямую: у = a — bx , где y – частная собственность, задействованная в производстве, x – государственная собственность, задействованная в производстве. Очевидно, что вся производимая в какой-то стране продукция выпускается на основе использования либо государственной, либо частной собственности, поскольку факторы производства – труд и капитал – также можно рассматривать в качестве чьей-либо собственности.

Все бесконечное множество возможных комбинаций соотношения частной и государственной собственности лежит вдоль линии: у = a — bx, длина которой 79 легко определяется по теореме Пифагора, поскольку мы работаем в декартовой (прямоугольной) системе координат правой ориентации. То есть линия, образованная функцией: у = a — bx , это гипотенуза в прямоугольном треугольнике, а длины катетов нам известны: по ординате длина катета противолежащего угла равна свободному члену нашего уравнения, а длина катета прилежащего a угла равна: , откуда длина гипотенузы искомого прямоугольного треугольника:

^C=^“ . Также длину гипотенузы мы могли бы сразу найти по формуле для длины дуги: c= ^^l + ^Ydx .

Площадь данного треугольника равна половине площади прямоугольника, построенного на его катетах:

fQx^dx = jJ(a + bx^dx . Это площадь характеризует область допустимых значений связи между государственной и личной собственностью, ограниченной сверху функцией у = a — bx , включая точки на ней.

Производственная функция в данной модели зависит от соотношения госу- дарственной и частной собственности: 2 = f(:x,y), и это поверхность в трехмерном пространстве x0yz. Поскольку область определения данной функции есть положительные числа как по абсциссе, так и ординате, которые связаны какой-то положительной функцией, то и по аппликате имеем положительное действительное число, характеризующее выпуск товаров и услуг при данном уровне соотношения государственной и частной собственности. То есть модель строится в первом октанте восьмиоктантной декартовой системы координат правой ори- ентации.

Возникает вид примет водственная

вопрос: какой конкретно данная нетипичная произ-функция? Для ответа на вопрос нам необходимо составить и решить подходящее дифференциальное уравнение. Задача упрощается в связи с тем, что переменная частной собствен- 79 ности линейно выражается через переменную государственной собственности, хотя при этом мы учитываем, что государственная собственность не детерминирует частную собственность, равно как и частная собственность не детерминирует государственную или коллективную собственность. Но нам ничто не мешает выразить один вид собственности через другой, подобно тому, как мы поступаем с товарами-заместителями или долями чего-то, поскольку доля от целого, то есть единицы, всегда равна:D2=1-Dt, где D^ + D2 — 1 .

Следовательно, изменение выпуска продукции (товаров и услуг) можно выразить через изменение государственной собственности, включив в модель непосредственно и частную собственность:

, поскольку или (a bx^) + x, где x – государственная собственность в условных единицах, y – частная собственность в условных единицах, а – свободный член уравнения, показывающий количество частной собственности, используемое при нулевой государственной собственности, то есть в условиях чистого капитализма; b – скорость изменения функции, показывающая в данном случае, на сколько единиц падает частная собственность при увеличении государственной собственности на единицу измерения.

Полагая, что как частная, так и государственная собственность с их ростом ведут к нелинейному увеличению выпуска продукции в правой части дифференциального уравнения первого порядка с разделяющимися переменными, мы можем использовать два эффекта, первый из которых назовем мультипликативным (то есть будем умножать), а второй аддитивным (то есть будем складывать). То есть при мультипликативном эффекте мы будем использовать произведение частной собственности на государственную (общественную, коллективную), а 80 при аддитивном используем простое их сложение. В обеих моделях нетипичная производственная функция будет нелинейной и похожей, но не идентичной (естественно), что продемонстрировано далее.

Сначала рассмотрим модель с мультипликативным эффектом. Общим решени- ем искомого дифференциального уравнения: — = (а — охух будет семейство

„      bx , axz , ^

кубических парабол: 2      3

, где C – произвольная постоянная.

Далее рассмотрим вариант с суммой, решив дифференциальное уравнение: de Г।

• — =   — ох) + х или то же самое:

dz ь ।।

• — = — bx + х + а , получив в итоге семейство квадратных параболических функций: ²¹ 2    2 ^аХ ^ .

Полученные на плоскости кривые внешне похожи, что видно из нижепред-ставленных графиков. Обе нетипичные производственные функции выпуклы относительно оси абсцисс.

Сначала проанализируем поведение производственной функции с мультипликативным эффектом, а потом проделаем то же самое и с параболой второго по-

Ьх2 х2

рядка: z = —— + — + ах + С , которая немного проще в анализе и интерпретации.

В нетипичной производственной функ-Ьх1 ах2 „ ции 2     3    2 имеет место мультипликативный эффект, а в функции

Пример производственной функции с мультипликативным эффектом

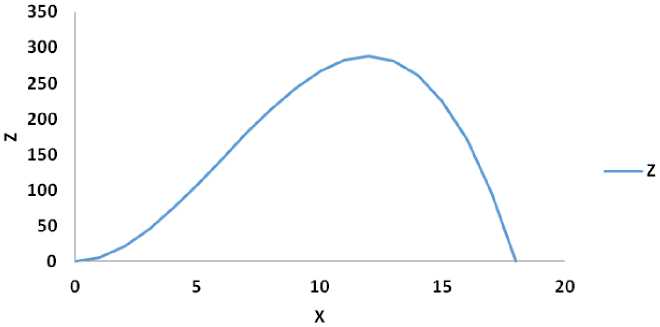
Рисунок 1. Пример производственной функции с мультипликативным эффектом из семейства подобных функций

Figure 1. An example of a production function with multiplicative effect from a family of similar functions

Пример производственной функции с аддитивным эффектом

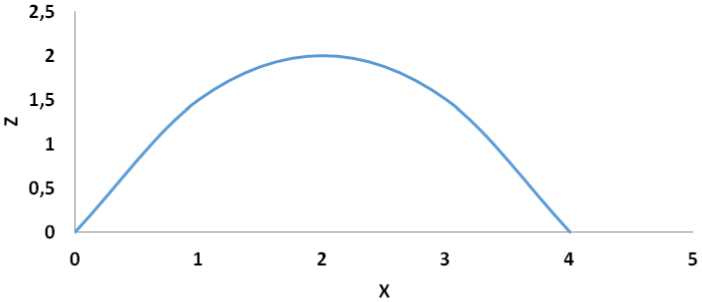
Рисунок 2. Пример производственной функции с аддитивным эффектом из множества подобных функций.

Figure 2. An example of a production function with additive effect from a set of similar functions.

Z 2^2^ ^^ + ^– аддитивный.

81 Поскольку при мультипликативном эффекте перед нами набор типичных кубических парабол вида:

, мы можем легко проанализировать их типичное поведение. Во-первых, здесь есть точка перегиба, в которой функция меняет вогнутость на выпуклость. То есть до точки перегиба вторая производная (ускорение) исследуемой функции положительна, а после ее прохождения отрицательна (начина- ется процесс замедления скорости движения). Первая производная данной функции (скорость) после прохождения точки перегиба остается положительной до достижения критической точки, когда она становится равной нулю, а за данной критической точкой первая производная функции меняет знак с плюса на минус, что свидетельствует о наличии максимума функции в данной точке.

Найдем критические точки функции

. Для этого возьмем сначала первую производную от данной с            — = ах — Ьх первообразной функции da и приравняем ее к нулю: ах — Ьх2 = О или Ьх2 — ах = О . Это неполное квадратное уравнение, имеющее два корл        ° ня: %! = и и %2 =7. Для нашего случая смысл имеет только корень %2 ь . В этой точке функция принимает максимальное значение. То а есть, подставив вместо икс значение ь , получим максимальное значение выпуска для данной производственной функции. Поскольку после прохождения точки , а

^Х2 ⁼ 7 производная меняет знак с плюса на минус, в данной точке имеет место максимум.

Чтобы найти точку перегиба, необходимо сначала взять вторую производ ную от функции или, что то же самое, – первую произ водную от функции              . По лучим: — = а — Лох, приравняв которую к нулю, получим: а — 2Ьх = О или а = 2Ьх, откуда критическая точка:

а

Т = —

.

2b

а

Подставив значение X = — в

Ьх3 ах2           2Ь функцию Z 3^2^^ получим значение функции в точке перегиба, когда ускорение в данном случае меняется с положительного на отрицательное, вогнутость функции сменяется выпуклостью. Поэтому до точки перегиба желательно активно наращивать государственную собственность, ибо это будет увеличивать экономический рост, то есть выпуск товаров и услуг, соответствующий данной нетипичной производственной функции.

Государственную собственность можно наращивать и далее вплоть до достижения функцией своего максимума, однако цепной темп прироста с каждым новым шагом будет уменьшаться вплоть до полной остановки. Если же и даль- ше продолжить наращивание государственной собственности за координату максимума, то пойдет быстрое падение экономики, то есть уменьшение выпуска 82 товаров и услуг, что хорошо видно из графика на рисунке 1.

Обратим внимание, если провести через точку максимума функции вертикальную прямую параллельную оси ординат, то функция относительно нее не симметрична, а имеет левостороннее смещение.

Рассмотрим теперь  нетипичную производственную    функцию:

bx^ x^

^Z + ^ + az + C , дающую, в отличие от мультипликативного, простой аддитивный эффект. В данном случае функция будет симметрична относительно своего максимума, в чем можно убедиться, начертив прямую параллельную оси ординат и проходящую через верши- bx^ x^

ну функции z = —— + — + ax+ C , что наглядно следует из графика на рисунке 2.

Согласно производственной функции bx² x^

• ²      2 "*" 2 "*" ^ "*" ^ выпуск будет

расти, но расти с замедлением и увеличением доли государственной собственности до достижения функцией своего максимума, после чего наращивание государственной собственности будет только понижать выпуск товаров и услуг. При этом с самого начала увеличение государственной собственности будет идти с замедлением. Сначала при увеличении доли государственной собственности мы будем видеть довольно большой прирост выпуска продукции, но на каждую последующую единицу государственной собственности выпуск будет уменьшаться, что уместно назвать законом убывающей производительности государственной собственности. При этом, в отличие от производственной функции с мультипликативным эффектом, в функции с аддитивным эффектом при прохождении точки максимума не наблюдается столь же резкого падения выпуска при дальнейшем наращивании доли государственной собственности в экономике, как это имеет место в функции с мультипликативным эффектом, но закон убывающей производительности государственной собственности в полной мере проявляется как в производственной функции с аддитивным эффектом, так и в производственной функции с мультипликативным эффектом, на что следует обратить пристальное внимание.

Чтобы обнаружить критическую точку для производственной функции с аддитивным эффектом, возьмем первую производную от первообразной функции: dz / bx² , x² ,       , p \        ,    ,     ,

• — =---1---hax + C = — bx + x + a

dx \   2     2             /

, получив простую линейную функцию. Приравняем производную к нулю: —bx + x + a = 0, и, решив уравнение, a получим критическую точку: x = :—.

Подставив полученное значение в исходное уравнение:

bx^ x^             .

z = —— + — + ax + C , получим максимальное значение производственной функции с аддитивным эффектом. Первая производная от этой производственной функции в данной критической точке пересекает ось абсцисс, поскольку именно здесь — = — bx + x + a = 0 .

Вторая производная здесь постоянна:

dx1 “ ’ поскольку не зависит от переменной икс.

Поведение нетипичной производственной функции с аддитивным эффектом показывает, что наиболее оптимально экономика работает при равном использовании государственной и частной собственности, тогда как поведение производственной функции, основанной на мультипликативном эффекте, предполагает более весомую роль государственной собственности в обеспечении экономического роста. С другой стороны, судя по поведению производственной функции с мультипликативным эффектом, наращивание государственной собственности за точку максимума функции ведет к резкому падению выпуска, в то время как в производственной функции с аддитивным эффектом поведение функции симметрично относительно точки максимума производственной функции.

Поведение нетипичной производственной функции с мультипликативным эффектом и производственной функции с аддитивным эффектом демонстрирует, что в экономике не желательно, а необходимо использовать как частную, так и государственную собственность. Использование только одного вида собственности, хотя и теоретически возможно, но приводит к нулевому выпуску по обеим производственным функциям, а следовательно, низкому уровню свободы в обществе, высокому спросу на инвэйдерные товары, включая, прежде всего, товары-преступления, как заместители нормальных товаров и услуг, что, впрочем, вынесено за скобки в данной работе.

Определенным недостатком модели нетипичной производственной функции с мультипликативным эффектом является то, что государственная и частная собственность определяются как равнозначные, но в качестве независимой переменной была принята государственная собственность. Если переменные поменять местами и выразить частную собственность через государственную, то нам придется вести речь о большей эффективности частной собственности, чем собственности государственной. Следовательно, наряду с законом убывающей производительности государственной собственности действует и закон убывающей производительности частной собственности.

В модели же с аддитивным эффектом положение переменных «частная собственность» и «государственная собственность» в исходном уравнении у = а — Ьх роли не играет. Следуя модели с аддитивным эффектом, необходимо просто стремиться к делению собственности на частную и государственную по принципу пятьдесят на пятьдесят. В этом смысле и государства должны быть государствами со смешанным типом собственности с соответствующей надежной охраной как частной, так и государственной собственности.

Поскольку смешанная экономика дает максимум выпуска по нетипичным производственным функциям, то это обеспечивает максимум экономической свободы народонаселения в данном государстве, а также возможность демократического политического режима с относительно низким уровнем преступности.

Как было отмечено ранее, поведение нетипичных производственных функций с аддитивным и мультипликативным эффектом является описательным, а не объясняющим. Объяснение же лежит за рамками рассмотренных выше математических моделей нетипичных производственных функций в законе добра и зла, в котором величина свободы определяется переменной, содержащей разницу между общественным и личным интересом. Положение устойчивого равновесия в модели закона добра и зла указывает на необходимость равномерного распределения частной и государственной собственности в нетипичных производственных функциях для достижения мак-

симума экономического роста при прочих равных условиях. В этом случае вектора личных и общих интересов максимально согласованы.

Анализ нетипичных производственных функций (их интерпретация) позволяет усомниться в выводах, которые сделал Фридрих Энгельс в своей монографии «Происхождение семьи, частной собственности и государства», когда частная собственность считалась источником общественных потрясений, а государство рассматривалось только как атрибут общества, расколотого на антагонистические классы. Ф. Энгельс, в частности, справедливо полагал, что частная собственность, классы и государство существовали не всегда, а возникли на определенной ступени экономического развития, но перспектива исчезновения государства и частной собственности 84 представляется сомнительной. Ф. Энгельс писал: «Государство существует не извечно. Были общества, которые обходились без него, которые понятия не имели о государстве и государственной власти. На определенной ступени экономического развития, которая была связана с расколом общества на классы, государство стало в силу этого раскола необходимостью. Теперь мы быстрыми шагами приближаемся к такой ступени развития производства, на которой существование этих классов не только перестало быть необходимостью, но становится прямой помехой производству. Классы исчезнут так же неизбежно, как неизбежно они в прошлом возникли. С исчезновением классов неизбежно исчезнет государство. Общество, которое по-новому организует производство на основе свободной и равной ассоциации производителей, отправит всю государственную машину туда, где ей будет тогда настоящее место: в музей древностей, рядом с прялкой и с бронзовым топором» [1, с. 79].

Но частная собственность столь же важна, как и собственность государственная (коллективная), ибо только их разумная комбинация обеспечивает процветание данного общества и государства, не забывая при этом каждого конкретного жителя данного цивилизованного госу- 84 дарства. При этом чистый капитализм и чистый коммунизм, сопровождаемые соответствующими типами государств, – совершенно неприемлемые способы совместного проживания больших масс народонаселения, а высокоразвитое государство с подконтрольной государственной собственностью является гарантом устойчивого развития и функционирования общества.